动态不确定性-药品物流多中心选址优化研究

袁志远, 高 杰, 杨才君

(1.西安交通大学 管理学院,陕西 西安 710049; 2.西安交通大学 药学院,陕西 西安 710061)

0 引言

2020年第三批国家组织药品集中采购规模达数百亿元,共有189家企业参与招标,中选企业125家,中选药品品规191个,平均降价53%。如何科学合理的布局药品物流中心,最大减少配送风险,把多企业、多种类、大批量、全国性、高时效的国家集采药品安全、高效的配送到需求城市成为药品物流急需解决的新问题。

近年来,有国内外部分学者对弹性供应链问题进行了研究。如:孟宏旭[1]考虑供应端网络结构的不稳定性和需求端需求量的波动性,建立混合整数线性规划模型。肖建华等[2]构建考虑节点应急能力的弹性供应链网络优化模型。SABOUHI等[3]构建了一个两阶段的可能性-随机规划模型。KAUR和SINGH[4]构建了环境可持续性的动态非线性混合整数模型。ELLURU等[5]构建一种具有时间窗的位置-路由模型。李真真[6]考虑供应商失效风险构建了弹性冷链供应链优化模型。KARMAKER和AHMED[7]采用模糊DEMATEL和SD方法,揭示了各指标与弹性水平之间的影响关系。王长琼和罗琦[8]构建了以供应链整体利润最大为目标的弹性供应链网络模型。JAFAR等[9]设计一个应对潜在风险的弹性供应链网络。

综合国内外文献,由于药品质控难度大,配送时效性强,技术含量高,传统的物流和冷链物流很难达到药品物流的标准要求。目前,还没有基于大数据思想,根据备选各地近20年受灾数据,针对全国性、多企业、多种类、大批量的药品集中配送弹性供应链的研究。

1 问题描述与模型建立

1.1 问题描述

基于国家药品带量集中采购背景,某药品物流企业承担了多家药品企业中选药品的配送。在备选的药品物流中心未来遭受灾害的概率已知的情景下,确定药品配送一级、二级药品物流中心及路径。

1.2 动态不确定性-药品物流多中心选址-路径优化模型

1.2.1 药品配送假设

我们假定:1)每种药品允许多家企业中标,允许一家企业多种药品中标,每种药品的采购量已知,每个城市药品采购量已知;2)药品企业到各药品物流中心的距离已知,各药品物流中心到各城市距离已知;3)建成各药品物流中心的储存空间能够满足日常需求;4)每种药品每月需求量匀速,药品n次配送完。

1.2.2 基本标记符号和参数

决策变量:

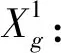
基于大数据思想,根据备选各地近20年受灾数据,在综合考虑药品配送安全性、配送成本、环保成本、时间满意度和实时路况下,动态不确定性-药品物流多中心选址路径优化最优模型[10,11]:

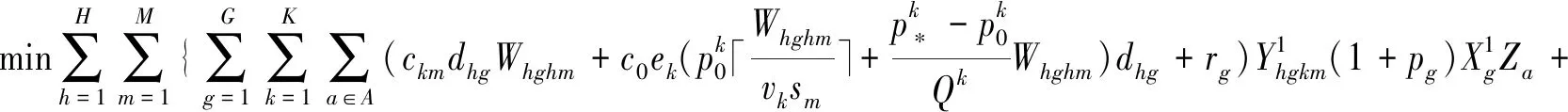
(1)

(6)

约束条件(2)表示中选的一级中心;约束条件(3)表示中选的二级中心;约束条件(4)物流企业可以选择多个一级、二级中心;约束条件(5)表示受灾中心的数量小于中选中心数量;约束条件(6)表示0-1变量。

1.3 药品物流中心未来遭受灾害的概率

本文基于大数据思维,根据二十年内当地出现的重大突发灾害次数与所选年限区间20的比值,作为未来该地区遭受重大灾害的预测概率。表达式为:

(7)

2 PSO-FCM-TS混合算法设计

本文采用PSO-FCM-TS混合算法进行求解[12-14],该算法充分利用了模糊C均值聚类算法,粒子群算法(PSO)和TS算法优点,提高了算法的收敛速度,增强了算法的寻优效能[15-17],PSO-FCM-TS混合算法流程[18-20]。

(1)用[0,1]间的随机数初始化隶属矩阵,使其满足公式(9)和公式(10)。

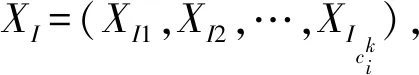
(3)计算隶属度矩阵。将x分成c(c>1,取正整数)类,模糊矩阵用U=(uij)表示,uij表示第j个样本点属于第i类的隶属度。uij满足以下条件:

uij∈[0,1],i=1,2,…,c;j=1,2,…,n

(8)

(9)

(10)

FCM目标函数J(u,A)定义如下:

(11)

其中,m>1是模糊加权指数,Ai是聚类中心。

FCM算法就是将目标函数J(u,A)最小化,在迭代过程u,A的取值公式如下:

(12)

(13)

dij表示样本Xj到类中心Aj的欧式距离。

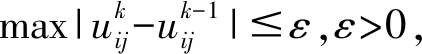
(5)将f(xl)=1/J(u,A)作为粒子群算法的适应度函数,每个粒子将其适应度函数值f(xl)与自己的最好值f(xpbest)进行比较,如果大于自己的最好值f(xpbest),用当前解代替历史最好解,然后,将其最好解的适应度函数值f(xpbest)与粒子群内最好解的适应度函数值f(xpbest)进行比较,如果大于群内适应度函数值f(xpbest),则将其作为当前的全局最好解。

(6)更新粒子的速度和位置。根据公式(14)和公式(15)计算粒子速度和位置,然后,转到(3)。

vi(t+1)=ωvi(t)+c1r1(pbesti(t)-xi(t))+

c2r2(gbesti(t)-xi(t))

(14)

xi(t+1)=xi(t)+vi(t+1)

(15)

(7)用当前最优解初始化禁忌解,初始化禁忌表及长度。

(8)令k=k+1,运行下一步。

(9)搜索领域产生候选解,比较当前领域中各解所对应的函数值,选取当前领域中最优的目标函数的解。当前领域中最优的目标函数与全局最优解的函数进行比较,如果小于全局最优解的函数,用当前最优解替换全局最优解,并更新禁忌表,否则,运行下一步。

(10)选取候选解中不被禁忌的最优解,并更新禁忌表。

(11)如果满足终止条件,输出最优解,结束;否则,转至(9)。

3 算例分析

3.1 模型及算法的验证分析

某药品物流企业承担了集采药品头孢拉定胶囊配送业务,参数取值及含义如表1,各城市编号为:1北京、2天津、3石家庄、4太原、5呼和浩特、6沈阳、7长春、8哈尔滨、9上海、10南京、11杭州、12合肥、13福州、14南昌、15济南、16郑州、17武汉、18长沙、19广州、20南宁、21海口、22重庆、23成都、24贵阳、25昆明、26拉萨、27西安、28兰州、29西宁、30银川、31乌鲁木齐。其中备选的一级中心为:北京、郑州、成都、杭州、广州;备选的二级中心为:长春、西宁、长沙、贵阳。各中心到各城市之间的距离通过高德地图软件获得。中标企业、药品规格、各城市的药品采购量依据国家第二次药品集采数据。假定此次集采药品分六批次配送完毕,求多企业多种类药品配送整体最优的中心选址方案。

表1 参数取值及含义

本文算法采用C++语言开发,其测试与运行均在CPU为2.5G、内存为8G和win10操作系统环境下进行。粒子数量:50,m设定为:2,禁忌表长:10,一级中心3个,二级中心3个,TS迭代次数1000次。要求24小时内配送到位,多企业多种类药品配送整体最安全、成本最优的配送方案如表2。

表2 多企业多种类药品配送最优方案

3.2 算法性能对比分析

为了验证本文所设计的PSO-FCM-TS混合算法有效性,采用多种算法进行计算,各算法参数设置如表3,运算结果如表4(计算时间取整)。

表3 各算法参数设置

表4 算法运算结果对比分析

通过实验我们发现PSO-FCM-TS混合算法与以上算法相比有较强的稳定性。

4 结论

本文以国家药品带量集中采购为背景,为提升国家集采药品集配的安全性和时效性,高效应对动态不确定性灾害。基于大数据思想,构建动态不确定性-药品物流多中心选址-路径优化模型,为提高算法精准度,设计了PSO-FCM-TS混合算法,最后通过真实案例进行了验证、对比和灵敏度分析。本文没有研究人为因素对药品配送的影响,因而,人为因素对药品配送的影响将是作者下一步研究的内容。