基于Charm算法挖掘基因表达保序子序列

2023-09-25廖旭红李志杰

现代计算机 2023年14期

廖旭红，江华，廖莎，李志杰

（湖南理工学院信息科学与工程学院，岳阳 414006）

0 引言

诞生于上世纪90 年代的分子生物学微阵列实验技术，通过生物芯片同时测定成千上万基因在不同实验条件下的表达量，产生了海量的基因表达数据［1］。挖掘基因表达数据中基因活动模式信息，在生物医药等领域有广泛用途。聚类是一种重要的无监督机器学习和数据挖掘技术，基因表达数据传统聚类仅在基因或实验条件单一方向上聚类。

然而，一个生物基因不可能在所有的实验条件下展示共表达特性，也不可能在所有的实验条件下展示相同的水平，却常常参与多种遗传通路。这些特性意味着基因表达数据存在许多潜在的局部模式，只有对基因（行）和实验条件（列）两个方向同时聚类，才可能挖掘出大量有价值的局部模式。

基因表达数据双聚类主要有基于定量测度和基于定性测度的方法。Cheng 等［2］引入元素残差与子矩阵均方残差（mean square residue，MSR）的概念，以MSR 为评价函数贪婪求解约束优化问题，这种CC 算法是典型的基于定量测度的双聚类方法。

多数双聚类方法通过不同基因表达样本相似性度量发现局部模式。Wang 等［3］为了指导相似模式聚类，定义了一种新的最近邻测度方法。Liu 等［4］以基因表达值排序的顺序而不是欧氏距离作为判断两个基因相似的标准，提出一种灵活有效的保序双聚类模型。保序子序列（order-preserving subsequence，OPSS）是部分行在部分列下具有相同的趋势，实质上是一种排序后的保序子序列挖掘问题。Ben-Dor 等［5-6］证明OPSS是NP难题。

本文提出基于Charm［7］的基因表达数据保序子序列挖掘算法Charm_Seq。Charm 是离线挖掘频繁闭合项集的最高效算法［8］。Charm_Seq 将Charm由频繁闭合项集挖掘改造为频繁闭合序列挖掘，实验验证了算法的有效性。

1 相关工作

1.1 基因表达数据保序子序列

基因表达数据可表示为一个n×m的数值矩阵A，其中元素aij表示第i个基因（g）i在第j个实验条件（t）j下的表达实数值。A可形式化表示为A=(G,C)，其中，G={g1,g2,…,gi,gi+1,…,gn}表示基因行集合，C={c1,c2,…,cj,cj+1,…,cm}表示实验条件列集合。表1是一个基因表达数据序列示例。

表1 基因表达数据序列示例

在DNA 微阵列分析中，密切相关的基因的表达值可能会随一组实验样本相应地同步上升和下降。尽管这些基因的强度表达水平可能不接近，但它们所呈现的模式却非常相似，这种模式即是双聚类局部模式。图1展示从GDS2267酵母菌数据集挖掘的两个局部模式示例，每个模式在条件列集上具有一致递减趋势。

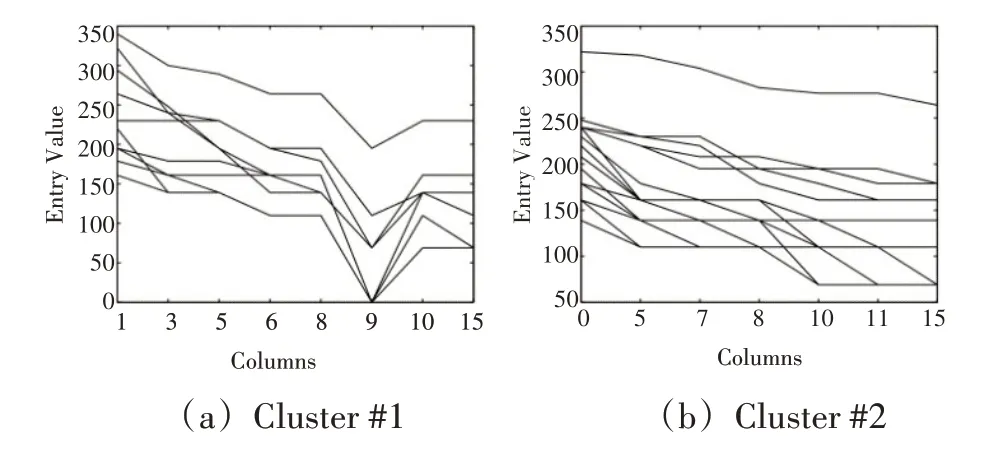
图1 酵母菌两个双聚类模式示例

假设I⊂G，J⊂C，AIJ=(I,J)表示部分行I在部分列J下具有相似行为或趋势，AIJ也称之为保序子序列。OPSS 是矩阵A的一种双聚类局部模式，挖掘OPSS 是要从给定的基因表达序列A中发现具有相似行为或趋势的子序列AIJ=(I,J)的集合。

1.2 频繁项集与Charm算法

项集挖掘以事务型数据为挖掘对象，是数据挖掘领域很活跃的研究方向。Charm算法挖掘事务型数据的频繁闭合项集，是最有效的离线频繁项集挖掘算法。

定义1事务型数据。事务型数据是由事务组成的集合，每个事务是项的集合，称为事务项集。设事务数据的属性集A={a1,a2,…,an}，项为属性的整型取值。每个属性在一个事务中最多一个项，因此，一个事务项集的长度不大于属性集长度。

定义2频繁项集。一个项集X在事务型数据的所有事务中出现的次数称为项集的支持度σ（X）。假设事务数据集的最小支持度阈值为min_sup，如果σ（X）≥min_sup，则称项集X为频繁项集。

定义3频繁闭合项集。假设X是频繁项集，Y表示项集X的任一超项集。如果∀Y，σ（Y）<σ（X）均成立，则称X为频繁闭合项集。

离线和在线频繁模式挖掘典型算法［9-10］有Apriori、Charm、IncMine、Moment 等。其中Charm是频繁闭合项集离线挖掘最有效算法，其优越性能主要通过构建<项集×事务集>键值对搜索树，并且键值对表示采用Bitset 编码技术。另外，算法采用差集技术减少中间计算节点的内存占用空间，使用基于hash 的方法加速清除非闭合的项集等。实验显示［9］，使用Charm 作为批处理挖掘器的IncMine 算法，比Moment 快几个数据级，且使用更少的内存。

Charm 的数据结构是一种Itemset-Tidse（tIT）前缀搜索树。树中每个节点为IT 对，频繁闭合项集为ITSearchTree 的叶子节点。该算法首先扫描事务数据库得到频繁项组成的集合I，然后对每个频繁项Xi∈I的节点Pi向下深度扩展。

2 基于Charm的频繁闭合序列挖掘

与Charm 挖掘频繁闭合项集不同，保序子序列OPSS 是挖掘频繁闭合序列，即保序子序列。挖掘频繁闭合项集与挖掘频繁闭合序列的区别如下：

（1）频繁闭合项集首先搜索频繁项，而频繁闭合序列挖掘首先搜索的是长度为2 频繁原子序列；

（2）频繁闭合项集搜索树下层节点由当前节点与兄弟节点连接生成，而频繁闭合序列增长由当前序列与长度为2频繁原子序列连接实现；

（3）长度为2 频繁序列是基本的原子序列，也是所有序列增长的连接对象。

然而，Charm有高效的Itemset-Tidset前缀搜索树数据结构，这是Apriori 等没有的。Charm_Seq 通过改造Charm 算法实现基因表达数据频繁闭合序列挖掘。

基于Charm 的保序子序列方法挖掘频繁闭合序列过程有如下三个步骤：

（1）每个基因的所有表达值按大小排序；

（2）各个基因表达值分别替换为相应列标签；

例如表1数据，经步骤（1）和（2）处理后将变成如表2所示的基因表达列序列。

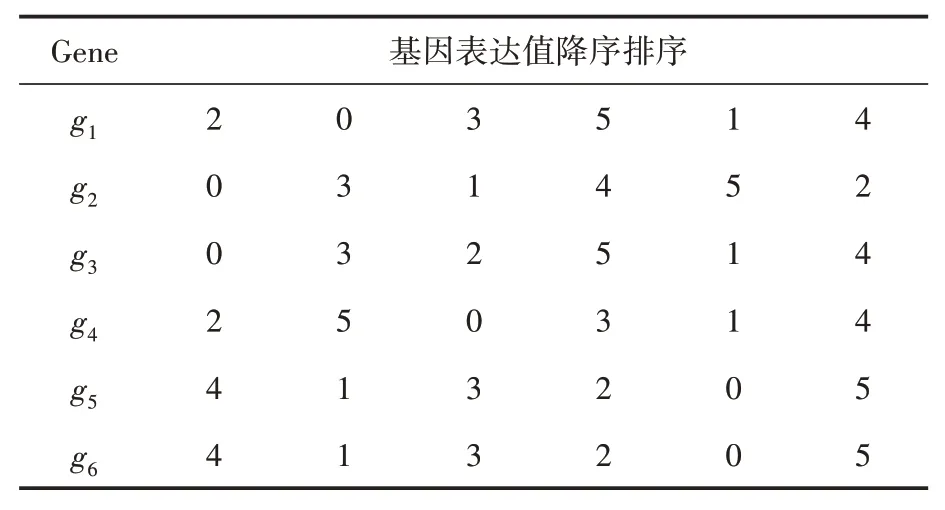
表2 基因表达列序列

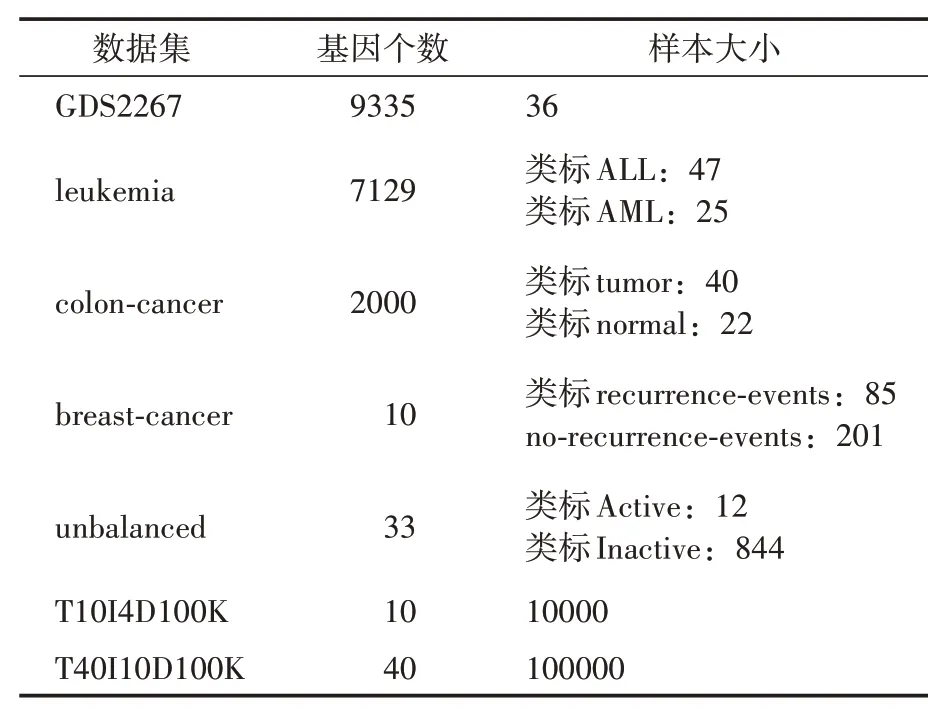
表3 实验相关的七个数据集参数

（3）挖掘列标签序列集的频繁闭合序列。

为了挖掘表2 中g1～g6的频繁闭合序列，可以改造Charm 算法为Charm_Seq算法，把挖掘目标由频繁闭合项集转变为频繁闭合序列。在Charm_Seq 算法中，设［P］表示以P为父节点的所有子节点，Pi∈［P］，则Pi向下深度扩展即是［Pi］不断取代［P］的循环过程。Charm_Seq 伪代码如算法1所示。

算法1Charm_Seq（A,min_sup,C=∅）

输入：基因表达数据矩阵A，最小支持度阈值min_sup

输出：频繁闭合序列集合C

以表2 中的｛g1，g2，g3，g4，g5，g6｝六个基因为例，图2 说明Charm_Seq 算法挖掘列标签频繁闭合序列的过程。

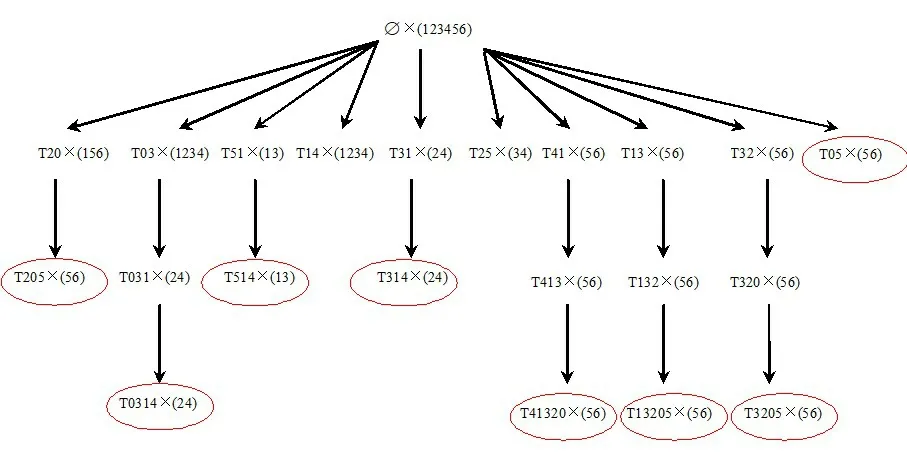
图2 g1～g6的列标签子序列×Gidset搜索树构建过程

3 实验结果与分析

本文使用GEO 微阵列基因表达数据集、基于基因表达数据的肿瘤或非肿瘤分类数据集，以及人工数据集对算法的性能进行评价。比较算法包括Charm_Seq、OPSS、CC、Charm、Apriori等。算法用Java 语言实现。实验在2.60 GHz、Intel（R）Core（TM）i7-6700HQ CPU、内存16 GB、操作系统Windows 10的计算机上进行。

3.1 数据集

GDS2267 微阵列基因表达数据集来自GEO网站：http://www.ncbi.nlm.nih.gov/geo，是GEO公共资源网上关于酵母菌（Saccharomyces cerevisiae）微阵列基因表达数据，数据集名称是Metabolic cycle:time course。该数据集以12～25 分钟的间隔对营养有限的连续培养细胞进行三个周期的分析。在这种条件下，生长的细胞以呼吸爆发的形式表现出强健的周期性。数据集对应实验的结果提供了对控制代谢振荡的分子机制的洞察。

四个基准数据集leukemia、colon-cancer、breast-cancer、unbalanced 是基于基因表达数据的肿瘤或非肿瘤分类数据集。其中，leukemia和colon-cancer 可从网站下载获得：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/。breastcancer和unbalanced 则是Weka 数据分析工具的两个自带数据集。

T10I4D100K 和T40I10D100K 是两个人工产生项集模式的事务数据集，使用Zaki’s IBM Datagen software 标准符号。该人工数据集句法规则为TxIyDz［Pu］［Cv］，其中x是平均事务长度，y为项集大小（单位为k），z表示所产生事务的数量（单位为k）。