基于编辑距离的字符串相似度算法研究
2023-09-25张胜楠
张胜楠
(湖北轻工职业技术学院信息工程学院,武汉 430000)
0 引言
求字符串相似度的算法在自然语言处理、抄袭检测、网页搜索等领域应用广泛,如编辑距离算法、最长公共子串算法、贪心字符串匹配算法、Heckel 算法等非常经典。当比较两字符串相似度时,编辑距离算法基于字面相似的方法计算,针对不同的需求对编辑距离算法改进的方法层出不穷,有作者考虑了非相邻字符间的交换操作,使编辑操作次数最小化;有作者从多公共字符串的熵出发来计算文本相似度等。这些方法往往只考虑他们的编辑次数而忽略了最长公共子序列(longest common subsequence,LCS)对字符串间相似度的影响,或者考虑了LCS但忽略了最长公共子串(longest common substirng,LCCS)的影响,使用传统的基于编辑距离求相似度的公式无法得到合理的结果。如情况一,字符串S=“abcd”与T1=“dcba”和T2=“cdab”比较相似性时,计算的编辑距离LD都是4,若不考虑LCS,就无法判断出T2与S更相似;再比如情况二,字符串S=“abcdef”与T1=“amcnf”和T2=“abcmng”比较相似性时,计算的编辑距离(levenshtein distance,LD)和最长公共子序列LCS都是3,所以即使考虑了LCS,也无法判断出T2与S更相似。
LCS是在字符相对位置不变的情况下并不要求必须连续,它反映了字符串的雷同性,常用于相似性检查。LCCS则必须是连续的最长的公共子串,对相似度计算具有一定的影响,本文提出一种基于LD综合考虑LCS和LCCS的字符串相似度算法,以改善准确性和适用性。
1 基于编辑距离的字符串相似度算法
1.1 基于编辑距离的字符串相似度计算
编辑距离由俄国科学家Vladimir Levenshtein于1965 年提出,以字符为编辑单位,计算由一个字符串到另一个字符串的最少操作(删除、插入、替换)次数,常被用于字符串的相似度计算。设两个字符串S=S1S2S3…Sm和T=T1T2T3…Tn,构造矩阵LD[m+1,n+1],使用动态规划的思想循环计算矩阵中每个单元格LD(i,j)的值,最右下角的LD(m,n)即为所求编辑距离大小,计算公式如下[1]:
Min = min{LD(i- 1,j) + 1,LD(i,j- 1) + 1,}LD(i- 1,j- 1) +f(i,j) ,其中,当S的第i个词不等于T的第j个词时,f(i,j)=1;否则,f(i,j)=0。LD本身就能表示两个字符串的相似程度,直观上LD越大,相似性越小。表示相似度Sim(S,T)的计算公式如下:
但其并不具备好的普遍适用性,例如设字符串S:abcdef,T:mefngh 则LD(S,T)=6,Sim(S,T)=1-6/6=0,两字符串的相似度却是0,显然不符合实际情况。
1.2 结合LCS和LD的字符串相似度算法
求解LCS长度的方法很多[2],如穷举法:对T串的所有子序列检查是否为S的子序列,从而确定是否为公共子序列,再选出最长的,但是对于两个长度分别为m、n的字符串,时间复杂度为指数级别的O(2n*2m);还有递归法:编程简单、易于理解,但由于有大量重复递归调用,效率不高。经典的动态规划的方法:将复杂问题简单化,引入数组来存放所有子问题的解,从而省去重复求解相同子问题的麻烦,当求LCS时,用L[i,j]记录序列Si和Tj的最长公共子序列的长度,最后,S和T的LCS的长度记录于L[m,n]中,建立递归关系如下:
当比较两个字符串S和T的相似度大小时,除了编辑距离LD的直观影响外,两字符串最长公共子序列LCS的大小也很重要,那么结合LD和LCS给出另一个相似度计算公式如下:
重新计算引言的情况一得:S(S,T1)=1/5 小于S(S,T2)=2/6,能正确地表示合理的相似度。经实验证明此公式有良好的适用性且拓展了传统公式的普遍适用性,但引言中提到的情况二仍未得到解决,下面结合最长公共子串继续对相似度计算公式进行改进。
2 基于LD、LCS和LCCS的字符串相似度优化算法
2.1 基于列向量的编辑距离求解优化算法
传统编辑距离算法的空间、时间复杂度都是O(m*n),考虑到每次计算LD(i,j)时只需用到LD(i,j-1)、LD(i-1,j)和LD(i-1,j-1),即只需要当前列和前一列参加计算即可,因此本文利用两个列向量代替矩阵,每次只保存当前的状态和上次运算的状态,实验表明在基本不影响结果和时间复杂度的情况下,空间复杂度减少为O(min(m,n))。
算法描述如下:输入:字符串S、T;输出:LD长度。
1.设n是S的长度,m是T的长度(设n 2.初始化v0[m+1]的值为0…m; 3.检查S(ifrom 1 ton)中的每个字符; 4.检查T(jfrom 1 tom)中的每个字符; 5.设cost 为编辑代价,ifs[i]==t[j],则cost=0;ifs[i]!=t[j],则cost=1; 6.设置单元v1[j]为下面的最小值之一: 7. 紧邻该单元上方+1:v1[j-1]+1 8. 紧邻该单元左侧+1:v0[j]+1 9. 该单元对角线左上角+cost:v0[j-1]+cost 10.在完成迭代(3,4,5,6)之后,v1[m]便是编辑距离的值。 考虑到当计算L[i,j]时只和L[i-1,j-1],L[i,j-1],L[i-1,j]三个元素直接相关,即在计算L[i]这一行的子问题时,只需要知道L[i-1]一行的值和当前L[i,j]的前一个元素L[i,j-1]的值即可,此时,在时间复杂度不变的情况下,空间复杂度由O(m*n)降低为O(n)。定义一个长为m+1 的数组base[]并初始化为0,一个递推前导front=0,一个当前计算元素pre(意义上的L[i,j]),每次计算完L[i,j]后,把front的值更新到base[j-1]上,然后把pre更新到front上,然后继续向后扫描,注意最后一个元素的更新。这样迭代n次,最后base[m]的值即LCS的值。 算法描述如下:输入:字符串S、T,输出:LCS长度。 1.输入两个字符串S,T; 2.定义数组base[]大小为T.length()+1,定义递推前导front=0,当前元素pre=0; 3.初始化base[]为0,base[i]=0; 4.检查S(ifrom 1 toS.length())的每个字符; 5.检查T(ifrom 1 toT.length())的每个字符; 6.循环检查若S[i-1]=T[j-1]则pre=base[j-1]+1;否则pre=max(front,base[j]); 7. 循环更新base和front,base[j-1]=front,front=pre; 8.更新base[T.length()]=front,检查base[j](jfrom 1 toT.length())并输出base[]值; 9. 循环(4,5,6,7,8)最后base[T.length()]就是LCS的值。 求解LCCS时,首先构造二维矩阵L[m+1][n+1]并初始化,若Si=Tj,则L[i][j]=1;最后找到矩阵中最长的斜对角线上为1 的字串就是LCCS,考虑到查找的麻烦,直接在矩阵需要填1时让他等于左上角值加1,这样矩阵中的最大元素就是LCCS的长度,LCCS的首字符位置就是第一个发生改变的单元格的坐标输出。 当考虑连续的最长公共子串LCCS的影响力之后,引言中的情况二就有了解决办法,在LD和LCS都相同时,可以通过比较LCCS来判断相似度,计算得LCCS(S,T1)=1小于LCCS(S,T2)=3,可以判断出T2和S的相似度更高,这也和人的主观判断方式相一致。设字符串S=“abcmg”,T1=“abcnp”,T2=“ebcmf”,现在发现这三个关键的影响因子大小都一样,但更接近人工主观判断的结果是S和T1更相似,本文的解决方法是综合考虑LCCS的长度和出现位置,引入一个变量p表示目标串S中最长连续公共子串的首位置,当LCS长度和LD大小都一样时,LCCS值越大则相似度越大;当LCCS长度也一样时,考虑到前驱字符(当前处理字符前一个字符)比后继字符(当前处理字符后一个字符)对相似度的影响更大,则p越小说明LCCS首字符位置越靠前相似度越大,μ是一个平衡此因子的变量,可以根据对LCCS需求的严格程度人为设定。定义新的相似度计算公式如下: 重新计算上面例子,设μ= 1,使用公式(5)计算Sim(S,T1)= 0.6,Sim(S,T2)= 0.563,得S和T1的相似度大于S和T2 的相似度,较之前结果更符合实际情况、区分性更好。 设字符串S和T长度分别是m和n,按照前文介绍的优化算法步骤求得编辑距离大小LD(S,T)和最长公共子序列长度LCS(S,T),按照LCCS算法步骤求得最长公共子串长度LCCS(S,T)和子串首字符位置p,其中过滤掉了无意义的全符号比较,按照提出的相似度公式计算相似度,Java语言实现,算法流程如图1所示。 图1 优化算法的计算流程 实验用两组数据分析算法的准确度、适用性和区分性。数据一选取源串S=“expect”,目标串集合W={w1,w2,w3,w4,w5,w6,w7}={“spectator”,“exercise”,“pecuniary”,“accept”,“excerpt”,“exempt”,“aspect”}。数据二源文本S=“abcde01234”,在英文词典中选出与word 接近的一组单词构成目标串T={t0,t1,t2,t3,t4,t5,t6,t7,t8,t9,t10,t11,t12,t13}={“wqefghlm56234”,“e01abcd”,“fbcdm56789”,“fghlm51234”,“mgcde05678”,“w01234abc”,“mghln01234”,“abcde56789”,“fghde01234",“abcde01567”,“fgcde01234”,“abcde012fg”,“fbcde01234”,“abcde01235”}。 分别采用公式(2)、公式(4)和公式(5)三个相似度计算公式求解相似度,对两组数据的字符串相似度计算结果进行对比分析,另外为了更详细地描述实验结论,便于比较说明,给出第一组的对比数据如图2所示。 图2 数据集W的相似度比较 可以看出,在对目标串集合w1~w8,t1~t13的考察中,公式(4)、公式(5)的结果较公式(2)更加合理精确,避免了由字符顺序变化导致的相似度极度不合理的情况,公式(5)求解的相似度和公式(4)走势大致一样,基本介于公式(2)和公式(4)的结果之间,说明了公式(5)的适用性和稳定性,当公式(2)、公式(4)两条线有重合持平时,即这两种方法无法区分相似度时,公式(5)的线条有上升或下降的变化,可以得到区分性更好的结果。 由表1 的第3、5 组数据可以看出,当LD相同时公式(4)、公式(5)较公式(2)有更合理、更具区分性的结果,由表第6、7、8组数据看出当LCS和LD都相同时,公式(5)较公式(2)和(4)得出了更合理且有区分性的相似度数据,数据因LCCS的长度和位置不同而变化,公式(5)相对于公式(2)、公式(4)有更适中的标准差和极差,使相似度结果更合理。 表1 数据对比 综上,可以看出公式(5)具有良好的普遍适应性,且比公式(2)和公式(4)结果更精确合理,结果具有更好的区分性。 按照提出问题、分析问题和解决问题的思路对字符串相似度的计算进一步改善。考虑到LCS和LCCS对计算字符串相似度的重要影响,基于编辑距离的相似度算法进行改进,改进的字符串相似度算法提高了算法的普遍适用性和结果精确性,对于差异性很小的字符串也可以得到较好区分性的相似度。另外,对LD和LCS的传统计算过程在数据结构方面进行了优化,在时间复杂度基本不受影响的情况下进一步降低了算法的空间复杂度。2.2 基于降维的最长公共子序列算法优化
2.3 基于LD、LCS和LCCS的字符串相似度优化计算方法
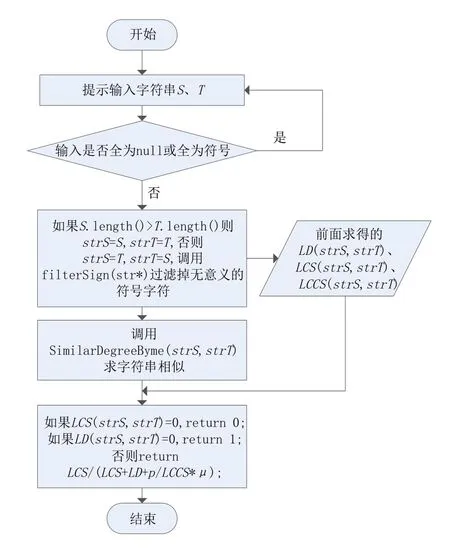
3 实验分析及结论
3.1 相似度结果分析
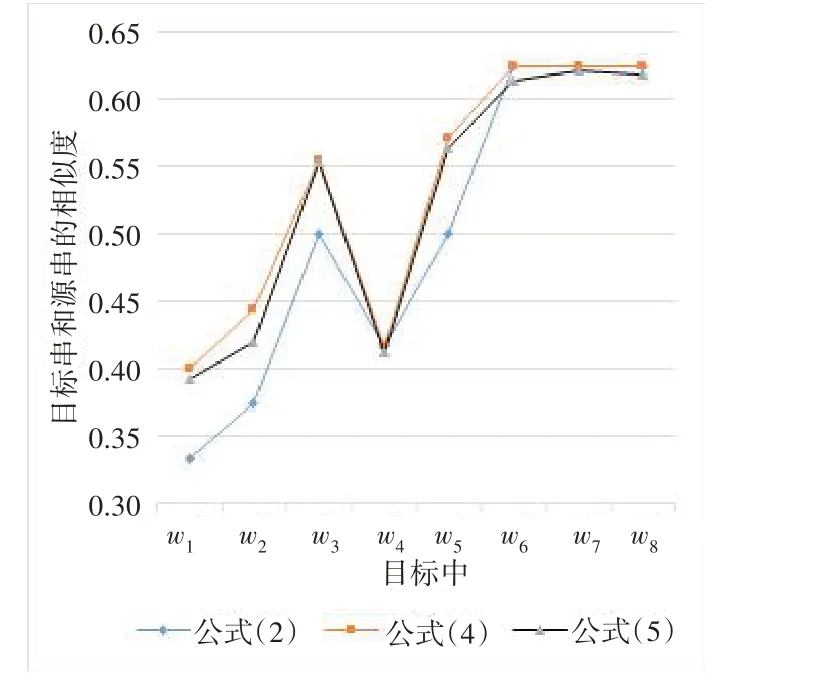
3.2 实验结论

4 结语
