旭龙水电站库区格亚顶堆积体变形及稳定性分析

杨 鹏,郑 光,黄 金 成,刘 震 东,陈 明 浩

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)

0 引 言

金沙江上游受构造破碎、岩体结构复杂、河谷深切、强卸荷改造等多种不良因素的叠合[1],区内地质灾害频发[2-3],如2018年金沙江上游西藏江达县白格村先后发生2次大型高位滑坡-堰塞堵江事件,造成巨大损失[4-5]。若修建水库,将促进该区域地质灾害的发育,威胁水库正常运行以及当地居民安全。据金沙江水电规划报告,金沙江作为中国最大的水电基地和“西电东送”主力,其上游将进行12级梯级水电站建设。旭龙水库位于金沙江干流上游河段,水库建成蓄水后可能发生库岸变形破坏等的工程地质问题[6-7],加之该区域地质环境差异大、新构造运动强烈、生态环境脆弱,若滑坡失稳下滑,将造成巨大损失和危害。

在国外,由于水库蓄水导致滑坡失稳的典型实例如瓦依昂水库滑坡[8],造成了灾难性后果,使大量学者开始关注此类滑坡。根据国内关于三峡库区典型滑坡的研究成果,水库蓄水后对滑坡的影响可主要归结为渗流特性研究和滑坡稳定性评价2个方面。比如大部分学者对三峡水库正常运行期间,不同的库水升降速率、滑体渗透系数对滑坡稳定性的影响进行研究[9-10],得出了一些影响稳定性系数的因素和规律。也有学者对滑坡进行流-固耦合的数值模拟计算[11-14],研究分析了滑坡的渗流特征及稳定性变化。在蓄水条件下,学者多关注某一水位或变化水位后的滑坡稳定性,但是对于水库蓄水正常运行后滑坡稳定性的动态变化以及滑坡变形预警模型的研究较少。坡体变形是直接反映滑坡稳定性和变化特征的重要参考。近年来,基于滑坡变形监测技术,采用滑坡变形切线角预警模型[15],对贵州省龙井村滑坡、甘肃黑方台黄土滑坡[16]进行了多次成功预警。滑坡变形切线角模型的实时过程化、无量纲化特点适用于几乎所有的渐变型或突发型滑坡,并取得了良好的预警防灾效果。利用该模型的普遍适用性,结合坡体稳定性系数的动态变化,可对库水位变化下的坡体变形阶段进行预测判别。

本文通过数值计算得到水库蓄水后旭龙水电站库区格亚顶滑坡堆积体的渗流特征、应力位移及稳定性系数动态变化,结合滑坡变形切线角预警判据,对水库蓄水后该坡体的变形阶段进行预测判别,对于旭龙水库地质灾害防治具有重要意义。

1 滑坡概况

旭龙水电站水库正常蓄水位2 302 m,总库容8.47亿m3,具有日调节能力。格亚顶堆积体位于金沙江干流上游河段右岸,属高山峡谷地貌,距离坝址约3.8 km。如图1所示,滑坡平面形态呈不规则形态,主滑方向约53°,平均坡度约30°。后缘高程约2 750 m,平均坡度约为47°,为崩塌形成的陡壁,两侧山脊有断层F6-1穿过,基岩裂隙发育,前缘直抵金沙江江面,高程约2 183 m。

格亚顶堆积体存在Ⅰ区滑坡堆积体和Ⅱ区崩塌堆积体两部分。Ⅰ区堆积平台位于坡体下部,为滑坡堆积体平台,高程约2 230 m。Ⅰ区组成物质主要为灰黑色粗粒土,岩性为花岗岩、变质岩碎石、块石,岩质新鲜、坚硬,粒径为0.1～0.5 m,见图2(a)。Ⅱ区堆积平台位于坡体中部、Ⅰ区平台左后侧,为上部的崩滑堆积体组成,高程约2 300 m。Ⅱ区物质组成为黄褐色块、灰黑色碎石土,主要为碎石、角砾及砾砂等,碎石岩性为石英闪长岩,间夹云母片岩,见图2(b)。水库建成蓄水后,正常蓄水位将达到坡体中下部,淹没到坡体下滑段,如图3所示。考虑水库30 m的波动水位,坡体受动水压力作用,将产生变形甚至失稳下滑堵江,威胁下游水库、村落和城镇。动水压力作用指水在土体孔隙中渗流时,对其周围骨架产生的渗透力,其大小与水力梯度成正比。如果动水压力指向坡外,将降低滑坡体的稳定性,从而引起滑坡复活[17]。本文将利用GeoStudio软件对格亚顶堆积体进行流-固耦合分析,预测其在库水位变动条件下的变形及稳定性。

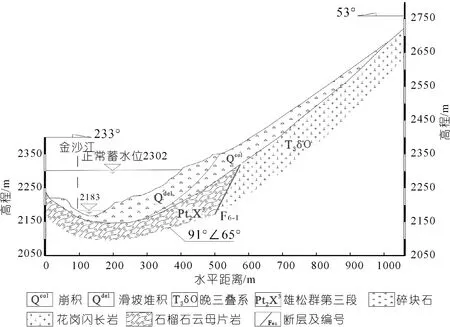
图3 格亚顶堆积体1-1′剖面Fig.3 1-1′ profile of Geyading accumulation body

2 库水位变动下滑坡数值模型

选用GeoStudio中的SEEP/W、SIGMA/W、SLOPE/W等3种模块相互结合的方式进行渗流-应力耦合分析,对蓄水后的格亚顶堆积体进行变形及稳定性分析。

2.1 模型构建及边界条件

根据工程地质资料以及水文资料,本文选取1-1′地质剖面建立数值模型,如图4所示。设计单元尺寸为10 m,共计3 699个节点,3 500个单元,并设置合理的边界条件。具体边界设置如下:① 初始渗流边界:将前缘坡面初始水位高程设置为天然江面2 183 m,底部为零流量边界,两侧边界为自由渗流边界,计算初始渗流状态。② 瞬态渗流边界:将前缘坡面设置为动态水头边界,水位以一定的速率升降,以此进行瞬态渗流分析。③ 位移边界:约束模型两侧的水平位移、模型底部的水平和竖向位移。④ 监测点:为了便于分析库水位变动过程中滑坡失稳的内在规律,设置监测点 A～D进行分析,其水位高程分别为2 230,2 272,2 302 m和2 320 m。

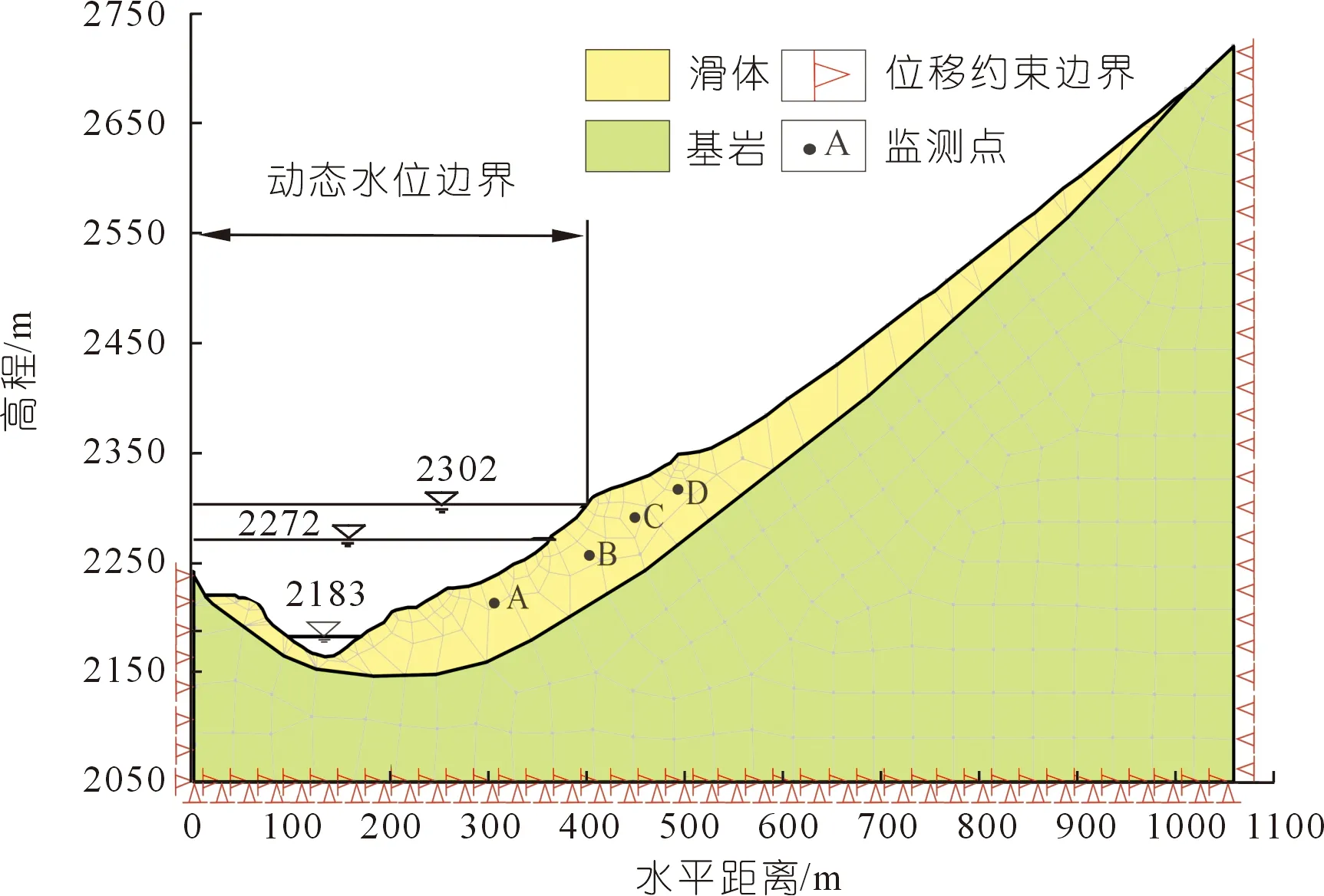
图4 计算模型Fig.4 Calculation model

2.2 参数选取以及计算工况

假定模型介质均为理想弹塑性材料,服从莫尔-库伦强度准则,材料的物理力学参数是通过室内试验、现场试验及工程类比等方法确定,物理力学性质参数见表1。运用SEEP/W模块自带的样本函数拟合得出岩土体的土水特征曲线(见图5);利用饱和渗透系数与土水特征曲线,结合Van Genuchten模型推导出渗透系数曲线(见图6)。考虑水库运行调度及库水位变幅特征变动范围为30 m,即2 183 m→2 302 m→2 272 m的库水位变动对滑坡变形及稳定性的影响。库水位以1 m/d的速率升降,动态边界水头函数如图7所示。

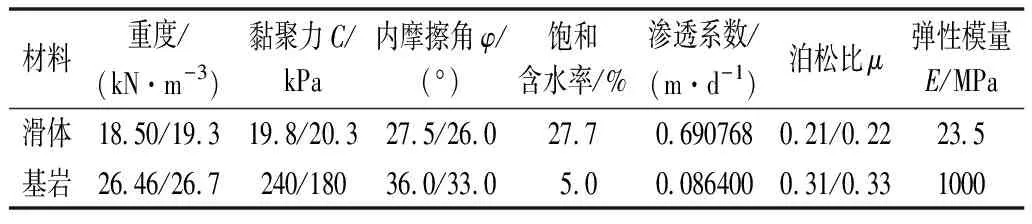
表1 岩土体物理力学参数取值Tab.1 Physical and mechanical parameters of rock and soil mass

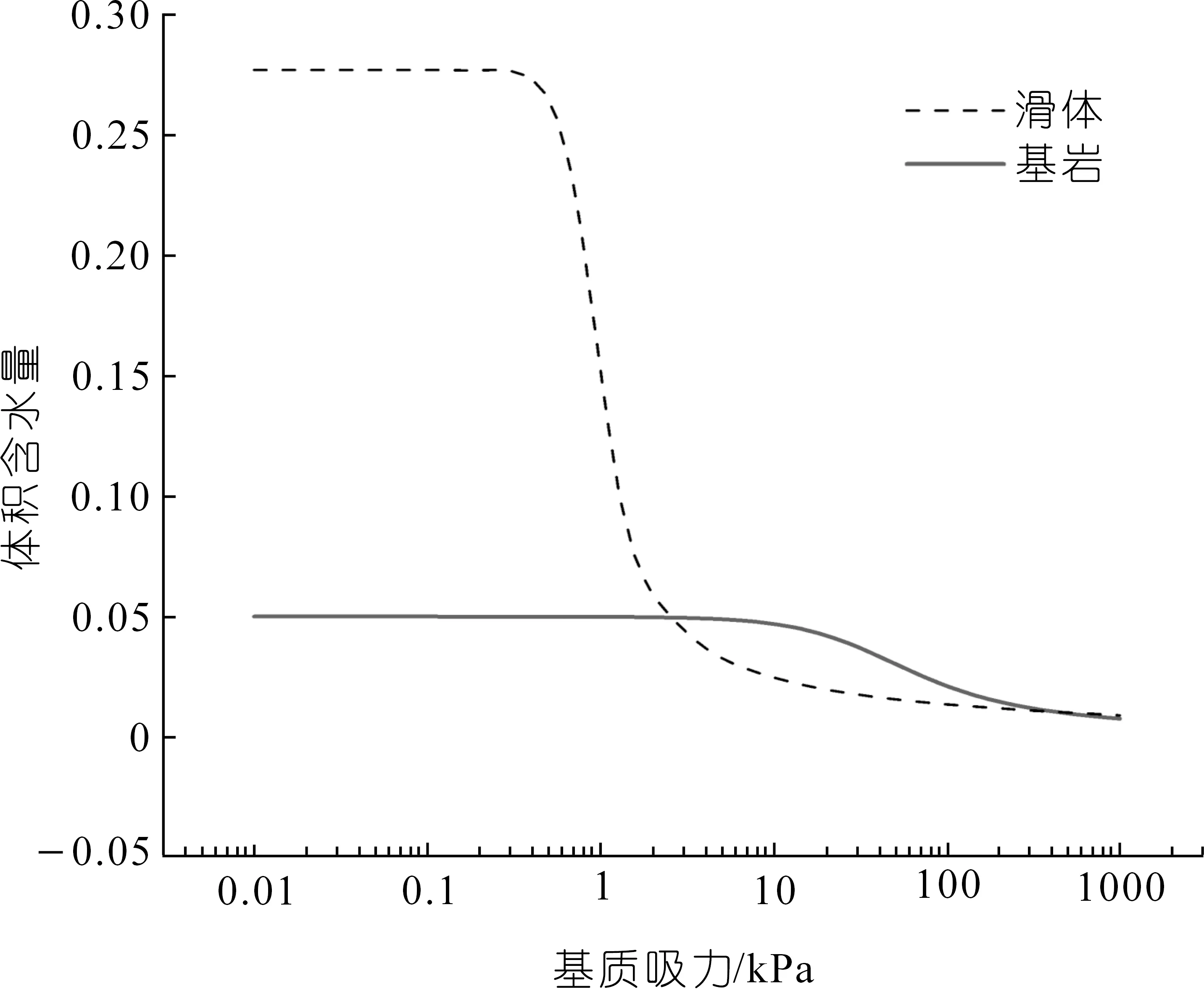
图5 土水特征曲线Fig.5 Soil-water characteristic curve

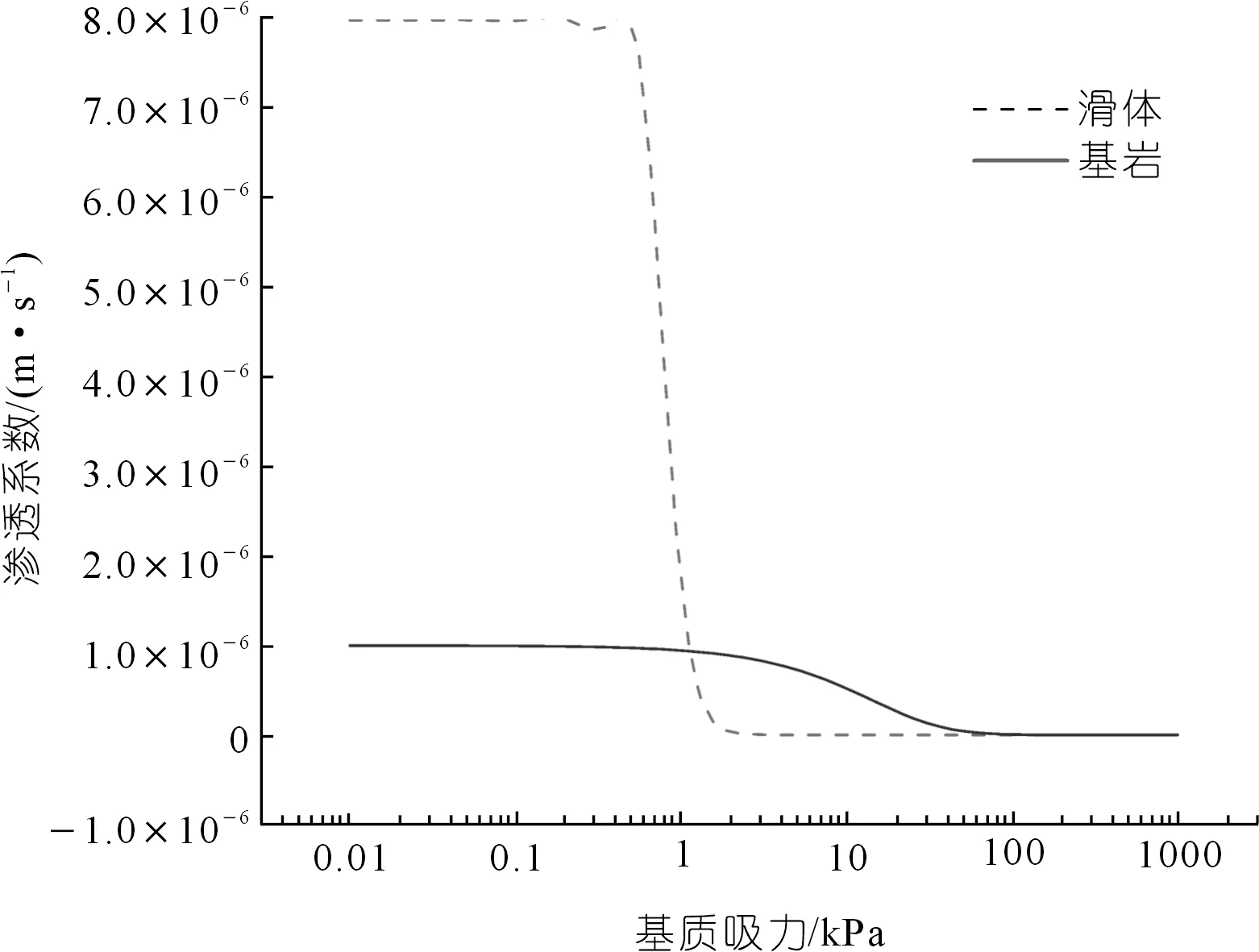
图6 渗透系数曲线Fig.6 Permeability coefficient curve

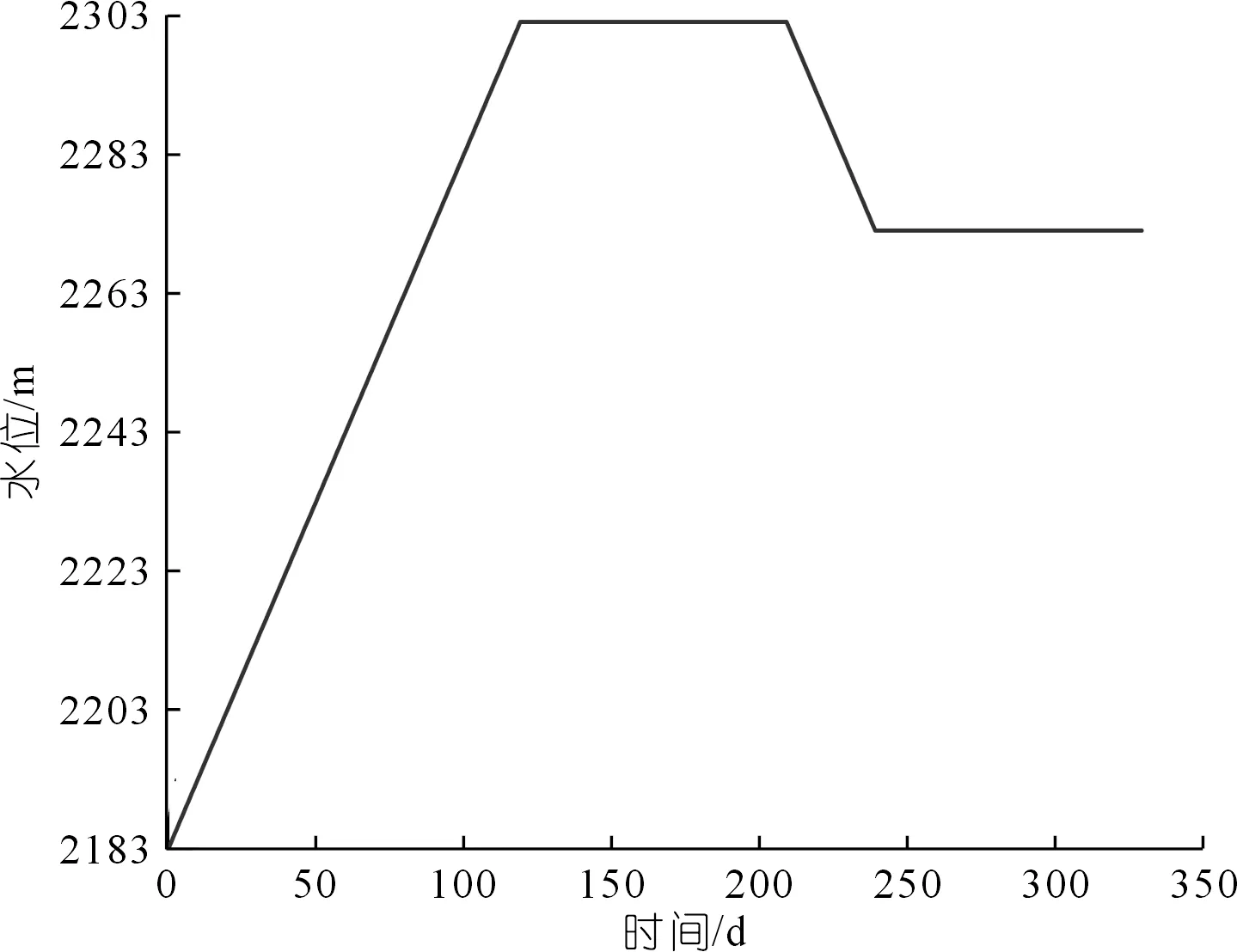
图7 动态边界水头函数Fig.7 Dynamic boundary head function

3 数值模拟结果分析

3.1 渗流场数值分析

由于水库运行,岸坡外的水位周期性变化较大,岸坡土体的饱和度也处于变化中,水分的相互补给改变了岸坡内的渗流场。斜坡岩土体的不均匀性和库水的渗透作用将直接影响岸坡的稳定性,所以,对库水作用下的渗流规律进行分析具有重要意义。

利用 GeoStudio 软件的后处理功能,得到瞬态渗流分析中地下水浸润线动态变化特征,如图8所示。浸润线指的是地下水位线中孔隙水压力为0的线条。各阶段浸润线变化特征如下:

1.1 材料 ①一次性无纺布，规格120 cm×120 cm、60 cm×60 cm各60块;②双层棉布，规格120 cm×120 cm、60 cm×60 cm各60块(在包布一角订一块3 cm×3 cm的“补丁”，用于记录使用次数);③3M压力蒸汽灭菌化学指示卡及指示胶带。

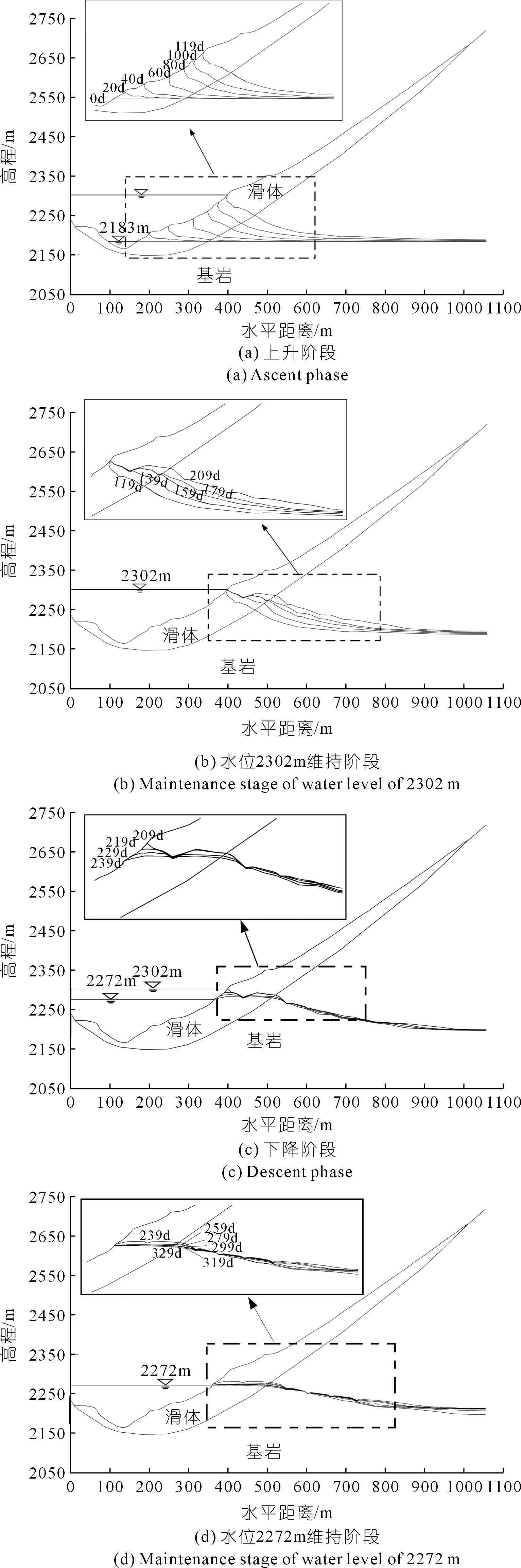
图8 水位升降过程中岸坡地下水浸润线动态变化Fig.8 Dynamic changes of groundwater infiltration line on bank slope during the rise and fall of water level

(1) 在水位上升阶段,如图8(a)所示,水位在上升过程中,因为坡体渗透速率明显小于库水升降速率,导致坡体内浸润线的位置明显滞后于库水位,上升时浸润线在坡面附近向下弯折,随着库水上升,这种滞后性在坡体中越明显,说明在水位上升过程中,水由坡面向坡体内逐渐补给。

(2) 在2 302 m水位维持阶段,如图8(b)所示,浸润线逐渐缓慢上升,明显还存在一定滞后性,这种现象在岩土体的渗透系数足够大时,将不再明显。与刚上升至2 302 m水位时相比,209 d浸润线上升明显。这种上升幅度随时间逐渐减小,并且在局部出现弯折重合的现象。

(3) 在水位下降阶段,如图8(c)所示,浸润线下降幅度随时间逐渐减小,在209～239 d期间,坡体浸润线向下弯折幅度较大,说明浸润线在水位下降阶段变化较大。

(4) 在2 272 m水位维持阶段,如图8(d)所示,浸润线在水位维持的90 d中逐渐缓慢下降,在坡体中浸润线的滞后现象已不明显。水位变动阶段相比于水位维持阶段,浸润线变化幅度大,这也使得应力在水位变动阶段出现明显变化(见图9～10)。

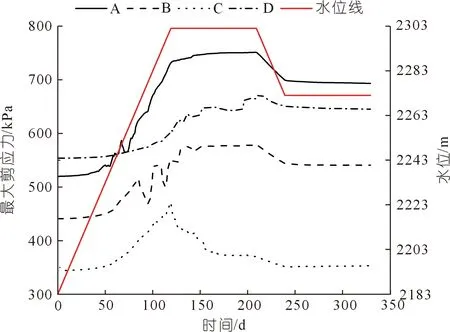
图9 监测点最大剪应力变化特征Fig.9 Variation characteristics of maximum shear stress at monitoring points

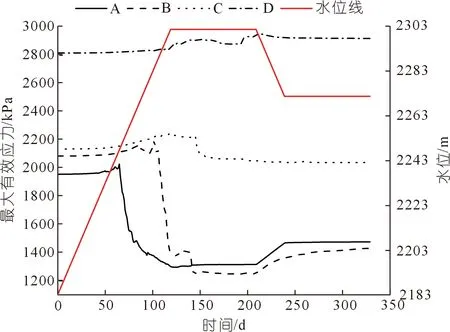
图10 监测点最大有效应力变化特征Fig.10 Variation characteristics of maximum effective stress at monitoring points

3.2 坡体变形分析

库水位升降引起坡体内部应力的变化,继而产生位移的变化。根据设置的监测点,库水位在升降过程中不同位置的最大剪应力、最大有效应力和位移变化如图9～11所示。各阶段应力-位移变化特征如下:

(1) 在水位上升阶段,各监测点的最大剪应力都呈急剧上升的趋势;最大有效应力在库水位未达到监测点高程前变化不明显,在水位上升至监测点高程附近时,最大有效应力开始急剧下降,如A,B,C点,而D点因高程位于库水位2 302 m之上,受库水作用相比于其他点较小,变化不明显。这说明在蓄水过程中,水位上升对附近岩土体应力场影响较大。

对于监测点的位移,各监测点位在库水挤压作用下首先表现出向坡体内部的位移,随后在库水位升高至监测点附近时,开始出现向坡外的位移。这是因为随着库水位升高,坡体受到指向坡外的动水压力作用,产生指向坡外方向的位移,也使竖直位移表现出持续增长的趋势。根据图11所示,在库水位上升阶段,坡体位移发生明显突变,在蓄水后可能在监测点高程附近出现局部失稳、滑塌。

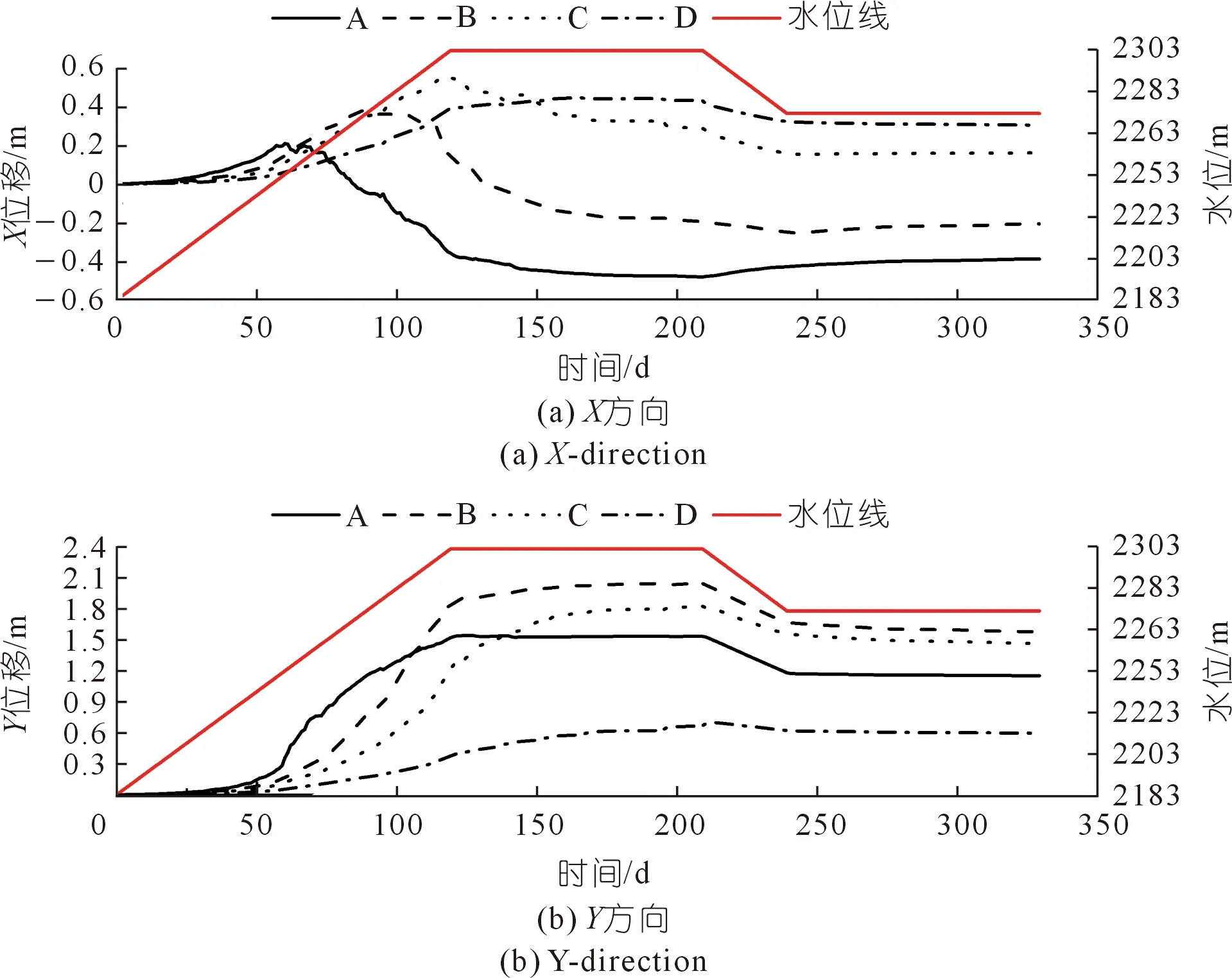
注:X和Y方向的位移以朝向坡外为正。图11 监测点位移随时间变化Fig.11 Change of monitoring points displacement with time

(3) 在水位维持阶段,坡体内应力变化不明显,逐渐趋于稳定,而各点位移则随着库水位维持一定时间后出现下降,并逐渐稳定在一定范围。这说明位移主要发生在库水位上升和下降阶段,而在水位维持阶段的变形较小。

3.3 坡体稳定性系数变化

(1) 库水上升并维持水位对坡体的影响具体可分为2个方面:① 水位上升阶段,坡体内的水位上升滞后于库水位(见图8(a))从而形成水位差,水向坡体内入渗,产生沿坡内方向的动水压力和孔隙静水压力,相当于施加在坡体表面的一个正应力,产生向坡内的位移(见图11),并且库水位以下部分受到水的浮力作用,下滑力减小,从而使稳定性系数上升,成为坡体稳定性的有利因素,如图12所示;② 水位维持阶段,水向坡体内入渗,土颗粒间的胶结物质被溶解,使土体黏聚力降低,土粒间的润滑作用增强使内摩擦角减小,即水的软化作用使土的抗剪强度降低,与基岩接触面(滑面)有效应力减小,抗滑阻力降低,成为对坡体的不利因素,使稳定性系数下降。

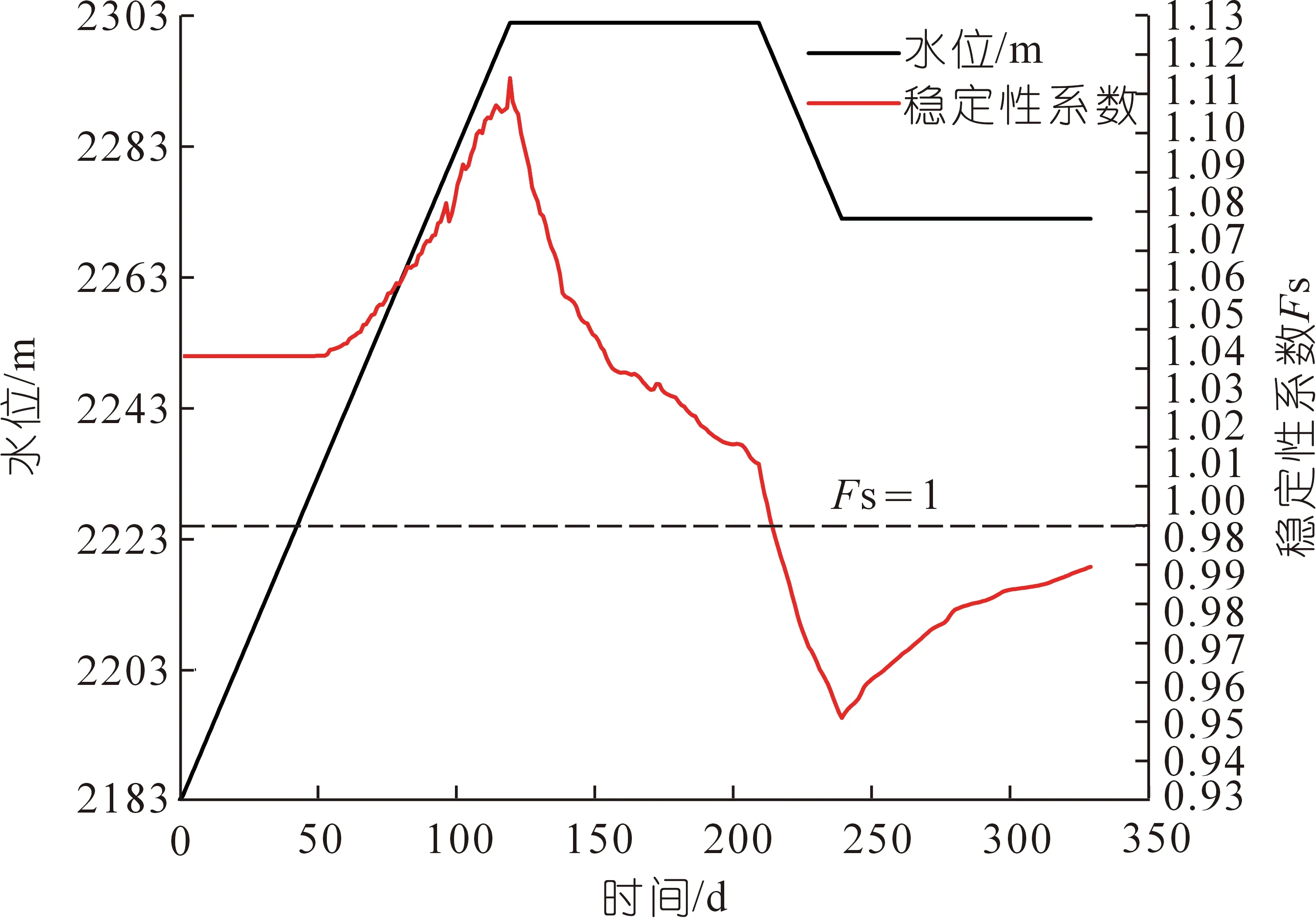
图12 滑坡稳定性系数与时间的关系Fig.12 Relationship between slope stability coefficient and time

(2) 库水下降并维持水位对坡体的影响。在水位下降阶段,由于岩土体的持水性主要与颗粒大小有关,颗粒越小的岩土体滞留的水越多,从而使浸润线的下降滞后于库水位,坡体内具有较高的孔隙水压且不能及时消散,形成非稳态渗流场,对周围土体骨架产生向临空面及向下的渗流动水压力(动态扩张力),同时,由水头差产生的静水压力相当于对前缘施加了一个推力,使坡体稳定性急剧下降,水位下降至2 272 m时稳定性系数减小至最低值0.951,此时最危险滑移面位置如图13所示。在2 272 m水位维持阶段,稳定性系数因为浸润线逐渐趋于稳定,形成稳态渗流场,并且应力位移变化较小,使稳定系数出现一定上升。

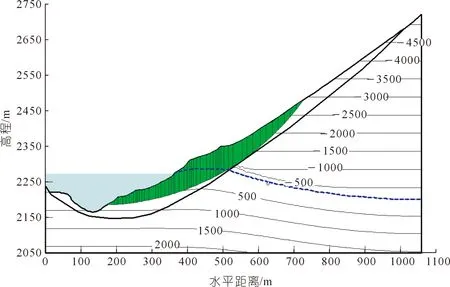
图13 最危险滑移面位置(239 d)(孔隙水压力单位:kPa)Fig.13 Location of the most dangerous slip surface (239 d)

在水库蓄水运行中,稳定性系数急剧下降的阶段并未出现在水位上升阶段,而是发生在2 302 m水位维持阶段和下降阶段,且稳定性系数最小的时间点出现在水位下降阶段。因此,在旭龙水电站蓄水运行后,应该关注蓄水初期以及库水下降过程中的滑坡变形情况,及时制定相应的灾害防治措施。

3.4 位移切线角预警判据

坡体从变形产生到最终失稳破坏,累计位移(S)-时间(t)曲线一般会经历初始(期)变形阶段、等(匀)速变形阶段和加速变形阶段,即所谓的斜坡变形演化3阶段规律[18]。位移切线角是指S-t曲线中某一时刻变形曲线的切线与横坐标轴之间的夹角,即S-t曲线上某一时刻用角度表示的曲线斜率。坡体在失稳破坏前的位移切线角一般为89.0°～89.5°,并以此作为滑坡的预警预报判据之一,即位移切线角预警判据。许强等[15]通过对斜坡累计位移-时间曲线进行坐标变换,实现纵横坐标同量纲化得到改良后的累积位移曲线。为满足预警需要,许强等对滑坡的加速变形阶段进行了细分,并给出了基于变形的滑坡4级综合预警判据,如表2所示[19]。

表2 滑坡预警级别的定量划分标准Tab.2 Quantitative classification criteria of landslide warning levels

改良S-t曲线处理具体方法如下[15]:① 通过位移累积曲线并结合坡体变形迹象,确定坡体等速变形阶段的变形速率,利用公式(1)得到改良后的位移-时间变形曲线;② 通过公式(2)计算出单位时间间隔的切线角。

(1)

式中:S(i)为某一单位时间段(一般采用1个监测周期,如1 d、7 d等)内坡体累计位移量;v为等速变形阶段的位移速率;T(i)为改良后与时间相同量纲的纵坐标值。

(2)

式中:αi为改进的切线角;ti为某一监测时刻;Δt为与计算S时对应的单位时间段(一般采用1个监测周期,如1 d、7 d等);ΔT为单位时间段内T(i)的变化量。

根据数值模拟得到的库水位变动下坡体的稳定性系数变化规律(见图12),选取库水作用带的监测点C的位移数据,利用单位时间步长记录的X,Y方向位移量,计算出单位时间间隔的切线角,如图14所示。

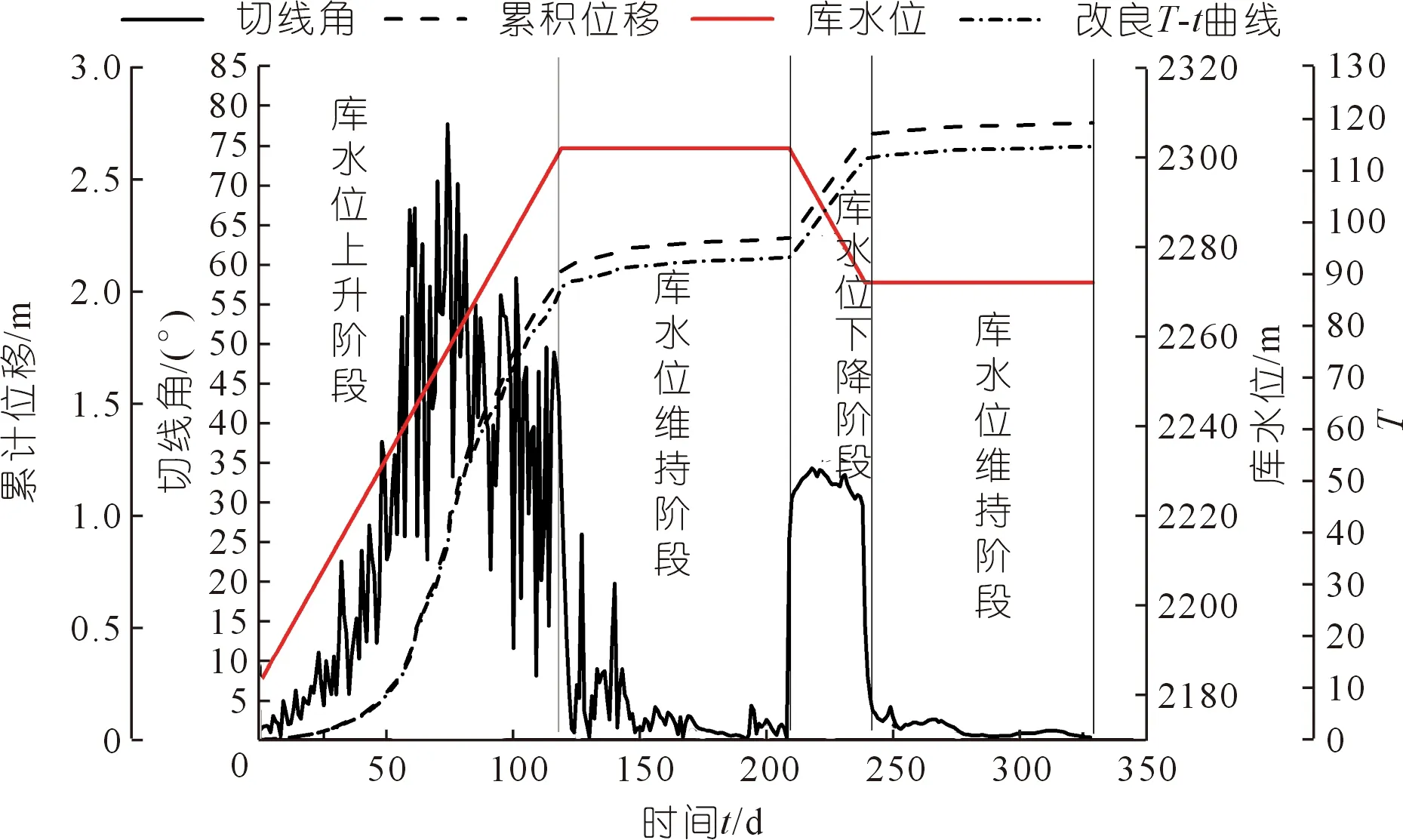
图14 点C的累积位移与切线角曲线Fig.14 Cumulative displacement and tangent angle curve at point C

利用位移切线角预警判据,根据滑坡预警级别的定量划分标准(见表2),判别坡体在蓄水后不同库水位作用阶段的变形状态。在水库蓄水运行后,切线角迅速增加,达到一定水位后开始下降,并且在库水维持阶段逐渐趋于平缓稳定。这说明在库水上升作用下,坡体变形速率突增,切线角明显增加。在库水下降阶段,切线角也有明显的突增,说明坡体在库水升降过程中变形较强烈,而在水位维持阶段则变形较小,与前文的应力-位移分析相符。该坡体在蓄水初期变形强烈,预测变形阶段为初加速变形,预警级为警示级,见表3。

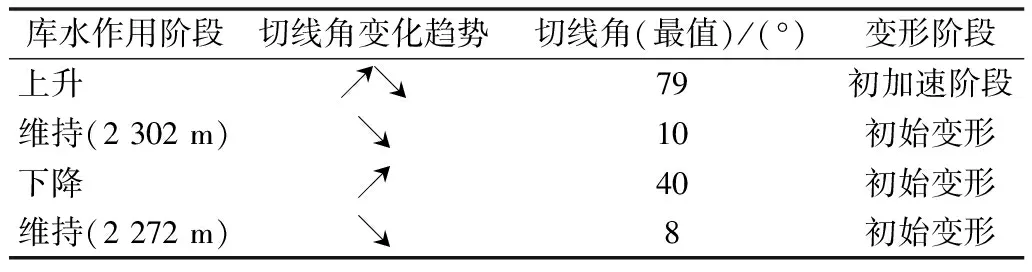
表3 滑坡变形阶段预测Tab.3 Prediction of landslide deformation stage

4 结 论

(1) 库水位变动影响着滑坡体的渗流场。在库水位上升阶段,库水向坡体内入渗,地下水位滞后于库水位,浸润线向坡内弯折凹陷;在库水位下降阶段,水由滑坡体向坡外排泄,浸润线向下弯折,并且下降幅度逐渐减小;在水位维持阶段,浸润线随时间趋于平缓,变化幅度逐渐减小,并出现局部弯折重合。

(2) 水库蓄水运行过程中坡体的应力-位移变化规律:最大剪应力与最大有效应力受库水位升降影响,在坡体内变化明显,突变主要发生在库水上升阶段。随着库水位上升,水平位移先增加后减小,竖向位移则逐渐增加。对水平位移影响较大的主要是水位上升阶段,而对竖直位移影响较大的主要是水位升降阶段。

(3) 水库蓄水运行过程中,坡体的稳定性变化规律:在库水上升阶段,因指向坡内方向的水压力作用和浮力作用,坡体稳定性系数明显上升;在水位维持阶段,因为受到库水的软化作用,岩土体抗滑力下降,稳定性系数减小;在库水位下降阶段稳定性系数继续减小至最低值0.951,而在2 272 m水位维持阶段则出现一定回升。

(4) 根据稳定性系数变化规律,结合数值计算获取的位移曲线,通过累加法计算出累积位移曲线,并利用切线角预警判据,对该坡体在库水位变动下的变形阶段进行预测判定。结果表明:坡体变形主要发生在蓄水初期,变形阶段为初加速变形,预警级为警示级。