非对称脉冲装置内部流动及能量损失特性

2023-09-25陈琪李伟季磊磊路德乐潘云欣

排灌机械工程学报 2023年9期

陈琪,李伟,2*,季磊磊,路德乐,潘云欣

(1. 江苏大学国家水泵及系统工程技术研究中心,江苏镇江 212013;2. 江苏大学镇江流体工程装备技术研究院,江苏镇江212009)

随着中国规模性浅层中层石油资源枯竭,石油进口量持续升高,对外依存度攀升,这不利于国家能源安全与发展.近年来,丰富的深部、超深部地层石油资源的发现,加速推动中国对深井、超深井勘探技术的探索.但是,钻探条件日益复杂,资源品位降低,导致钻井过程中消耗大量的时间和能源成本,同时整个过程中存在着不同量级的风险.石油勘探逐渐向地层深部发展的过程中,稳定高效的钻井作业显得尤为重要[1-2].

钻头机械钻速低是制约深井、超深井钻探作业高效安全的一个重要因素.负压脉冲辅助钻井技术是利用调制装置将连续流动转换成脉冲射流,使井底形成一定范围的负压脉动,可以有效改善井底围压环境,改善井底钻头及岩石的受力状况,从而提高钻头机械转速[3].文献[4]将空化空蚀破坏作用引入脉冲射流装置中,并与自振空化射流耦合,试验表明不同环境、多工况下装置的适应性较好,装置性能稳定,机械钻速明显提高.负压脉冲辅助钻井技术的优越性在实践中已得到大量验证[5].但是,目前脉冲装置调制的井底流场大多属于均匀对称流场,不能充分发挥脉冲射流装置的性能.

非对称脉冲射流装置对进一步提高井底清岩速度和钻井效率具有重要意义.谢翠丽等[6]对非对称多喷嘴平底钻头井底三维流场进行了数值模拟,发现非对称布置改善了井底流动状况.张建秀[7]研究了一种基于科安达效应的非对称脉冲调制装置,发现随着岩样的强度增大,非对称脉冲射流较普通直射流岩样渗透率显著提高.但是,目前对非对称脉冲射流装置的能量损失研究相对较少,并未充分发挥装置的性能.对于调制高效稳定的非对称井底流场的技术研究依然不成熟.

文中利用计算流体力学方法研究一种非对称脉冲射流装置,基于熵产理论分析非对称脉冲射流装置各个部件能量损失规律,揭示叶轮和盘阀间隙对装置的性能影响,为高效非对称脉冲射流装置设计提供理论参考.

1 熵产理论

(1)

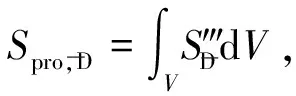
(2)

(3)

在数值计算方法中,脉动速度分量引起的熵产率不可直接获取.将湍流模型中湍流耗散率ε与脉动速度分量产生的熵产率建立联系[8-9],由脉动速度引起的局部熵产率计算式为

(4)

由于在计算近壁面区域时熵产存在较大误差,引入壁面熵产求解方法,即

(5)

式中:τ为壁面切应力,Pa;vo为近壁面速度,m/s.

2 装置的结构与数值模拟

2.1 装置结构和工作原理

非对称脉冲射流装置主要由导流块、水动力叶轮、轴承、轴、动/静盘阀6部分构成,如图1所示.

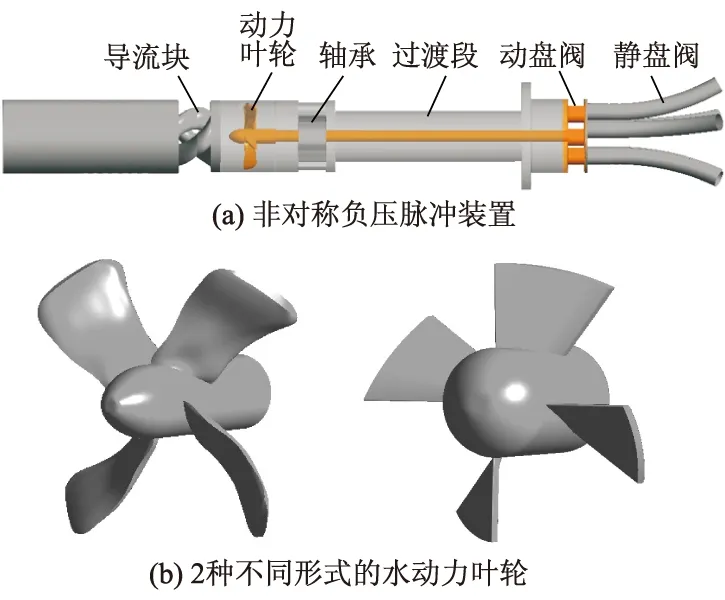
图1 装置的基本结构

图1b左边为初始叶轮,其采用导流块正冲形式,旋转方向为逆时针.右边为新型轴流叶轮,其采用导流块反冲形式,旋转方向为顺时针方向.2种水动力叶轮外径为76 mm,叶片数均为4,其中,初始叶轮轮毂最大直径为16 mm,新型轴流叶轮轮毂最大直径为30 mm.装置最大通流面积为0.004 9 m2.动盘阀、静盘阀选取最优通道数组合分别为3通道和5通道.其工作原理:高压水由装置入口流经导流块产生高速流动的流体,流体冲击叶片带动水动力叶轮旋转,并通过连接轴驱动动盘阀低速旋转,利用动盘阀通道与静盘阀孔口的匹配关系,在出口处产生瞬时非均匀的脉冲射流,井底处形成二次正态分布的非均匀流场.从而大幅度提高流体的集中冲击强度和减少井底“压持效应”,使井底携岩效率和钻头机械钻速大幅度提升.

2.2 数值模拟

文中采用商用软件ANSYS-ICEM对计算域复杂的进口区域水体和叶轮区域水体行了非结构化网格划分并局部加密,同时对轴承区域水体、过渡区域水体和动静盘阀区域水体进行六面体结构化网格划分,如图2所示.

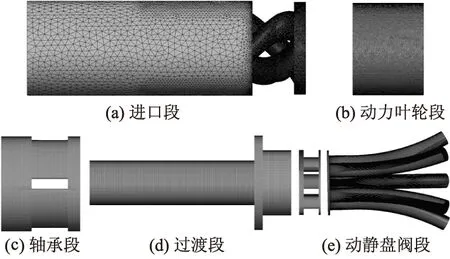
图2 装置水体网格划分

考虑到盘阀间隙处大小不等,间隙处网格层数不低于10层,由于间隙处网格单元宽度较小,应保证网格长宽比例在合适范围内,最大不超过3∶1,动盘阀和静盘阀交界面处尽可能控制网格大小相似,网格数从800万至1 000万.最终网格质量均在0.4以上,经过网格检查,计算区域网格的质量达到计算要求.利用计算流体力学软件CFX对非对称脉冲射流装置进行全流场数值模拟.采用半经验性的双方程标准的k-ε湍流模型进行数值模拟,二阶迎风格式求解.假设流体介质为不可压缩的25 ℃水.在计算域上,进口设置为质量流量32 kg/s,出口设置为自由出流,无滑移壁面条件.考虑到新型轴流叶轮与初始叶轮在设计工况下具有相似的扭矩,叶轮域转速均为最优设计工况下的60 r/min.

3 结果与分析

3.1 2种水动力叶轮的装置性能及能量损失特性

3.1.1 2种水动力叶轮下装置的性能

水动力叶轮是非对称脉冲射流装置的核心驱动部件,不同形式的叶轮对装置稳定高效运行具有重要意义.新型轴流叶轮与初始叶轮在设计工况下具有相似的驱动力.图3为新型轴流叶轮和初始叶轮下非对称脉冲射流装置单孔出口处压力pout和速度v变化.

图3 动盘阀转动角度与出口压力和速度关系曲线

由图3可以看出,在单个旋转周期内,动盘阀每旋转120°单个孔口形成一个水力脉冲,速度和压力达到一次最大值.其原因是动盘阀三通道和静盘阀单孔口在一个旋转周期内完全契合3次.当静盘阀孔口与动盘阀通道完全契合时,压力与速度达到极大值.采用初始叶轮装置的最大脉冲速度达到47.58 m/s,最大压力脉冲幅值为1.08 MPa.采用新型轴流叶轮装置的最大脉冲速度达到47.22 m/s,最大压力脉冲幅值为1.07 MPa.在单个周期内,2种形式的叶轮对出口处压力和速度波动相似,脉冲幅值变化幅度相似.可以得出,叶轮处的流动状态对钻孔出口处的影响较小.

3.1.2 2种水动力叶轮下装置能量损失特性

传统的基于压降计算的井底脉冲射流装置的损失计算方法无法准确地确定损失位置.文中从熵产理论和热力学第二定律的角度研究了脉冲射流装置中的能量损失,设计工况下采用不同类型水动力叶轮的非对称脉冲射流装置叶轮内流动特性及熵产分布具有较大差异.分析能量损失的主要原因及损失的关键部位,对选取高效能叶轮具有重要意义.

图4为2种水动力叶轮下装置各流道3种类型熵产分布.可以看出,整个装置内脉动速度引起的熵产是各过流部件能量损失的关键因素,其次是壁面熵产,时均速度引起的熵产远小于前两者.静盘阀区域熵产占装置总熵产比率最高,其次是动盘阀区域,叶轮区域熵产相对较高.初始叶轮的脉冲射流装置叶轮段总熵产为33.90 W/K,初始叶轮的脉冲射流装置总熵产为229.92 W/K.新型轴流叶轮的脉冲射流装置叶轮段总熵产为28.72 W/K,新型轴流叶轮下装置的总熵产为221.42 W/K.从熵产角度分析,采用轴流叶轮的脉冲射流装置能量损失优于采用初始叶轮的脉冲射流装置.

图4 不同叶轮下各流道3种类型熵产分布

3.1.3 2种水动力叶轮内流动特性及熵产率分布

为分析2种不同水动力叶轮下装置叶轮段脉动速度引起的熵产差异,对叶轮段内流动特性及熵产率分布进行分析.图5为初始叶轮与轴流叶轮内部速度流线图.

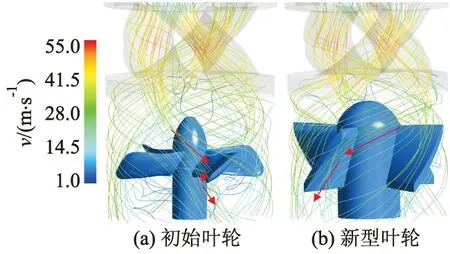
图5 不同叶轮下速度流线图

由图5可以看出,采用初始叶轮装置入口流体经导流块加速后,叶轮入口液流角相对叶片位置近似垂直,水流直接冲击叶轮后向两侧流动.采用新型轴流叶轮入口流体经导流块加速后,叶轮液流角相对叶片位置为锐角,流体冲击叶轮后向斜下方流动.整体上,初始叶轮内部流线更为紊乱,新型轴流叶轮内部流线相对较为规整.可以得出,相较于新型轴流叶轮,初始叶轮流场内存在更多的紊乱流动导致的能量损失,这与上述采用初始叶轮装置脉动速度引起的熵产大于采用轴流叶轮装置相吻合.同时,由于轴流叶轮和流体接触面积更大,壁面剪切力也较大,轴流叶轮的壁面熵产值略大于初始叶轮.

图6为0.3,0.5,0.7倍叶高处初始叶轮内局部熵产率Se和速度矢量布图.

图6 初始叶轮不同叶高下熵产率分布

从图6可以看出,在不同叶高下叶轮吸力侧均有旋涡存在,较高的熵产率分布在叶片压力侧附近和叶轮进口处.分析可得,叶片压力面熵产率较高的原因是水流冲击叶片造成的冲击损失.叶轮进口处存在一部分水流冲击叶片出现回流现象,在叶轮进口处产生的旋涡,并出现了较高的熵产率.叶片背部旋涡的存在是叶片两侧存在较高熵产率分布的主要原因.

图7为0.3,0.5,0.7倍叶高处新型轴流叶轮内局部熵产率分布图.可以看出,采用反冲方式的新型轴流叶轮与初始叶轮相比较,在0.3,0.5倍叶高下熵产率分布较优,其主要原因是新型轴流叶轮叶片对高速流体流动阻碍作用较小,过流能力更强.从0.3～0.7倍叶高处,叶轮流域速度分布从紊乱趋向平滑,在较大叶轮半径下水流做功能力更强,水流驱动力更有效.相同性能下,由于新型轴流叶轮叶片安放角与高速水流冲击角度接近,流体通过能力优于初始叶轮,叶轮内部冲击损失和湍流耗散相比初始叶轮效果更优.因此,水动力叶轮结构参数是引起水动力叶轮段能量损失的主要因素.

3.2 新型轴流叶轮下装置内部流动及能量损失

3.2.1 新型轴流叶轮下装置内部流动特性

采用上述高效新型轴流装置对脉冲射流装置内部流动及能量损失特性进行进一步分析.前期研究发现,设计工况下无导流块装置无法驱动叶轮正常旋转[10].图8为叶轮域进口处到叶轮域出口处不同轴向距离的截面图,水流经过导流块在叶轮区域进口处产生较强预旋作用,使得水动力叶轮获得更高的水力扭矩.

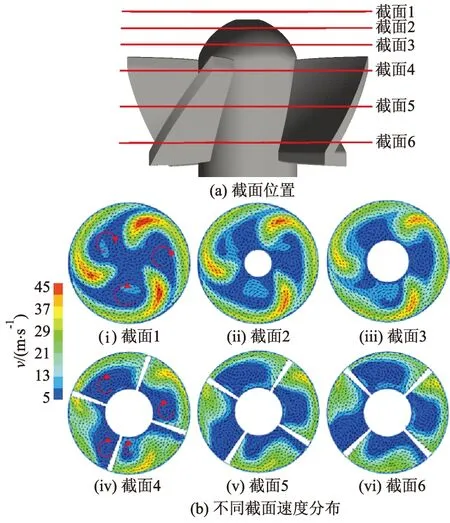
图8 水动力叶轮区域内速度截面图

随着轴向距离的增加,截面处最大速度逐渐减小,高速水流动能转化为势能.同时由于高速旋转水流的存在,在叶轮区域进口处管道中心处形成与预旋方向一致的顺时针旋涡.从叶轮域进口至叶轮出口处各截面图相似位置均有旋涡的存在,可以推断出叶轮域内靠近中性轴处存在从进口处到叶轮出口处的螺旋状涡.叶轮流道内螺旋状涡的存在造成流道内压力脉动,水动力叶轮受到流道内压力波动影响,产生扭矩波动.

水动力叶轮是驱动盘阀的唯一动力源,叶轮转动的稳定对脉冲射流装置出口脉动分布至关重要.图9为新型轴流叶轮在设计工况下单个周期内扭矩M波动随叶轮转动角度的变化.新型轴流叶轮扭矩在-0.10～0.15 N·m波动,扭矩波动幅值仅占平均扭矩的3.27%.扭矩波动幅值较小,新型轴流叶轮可以在低转速下稳定运行.

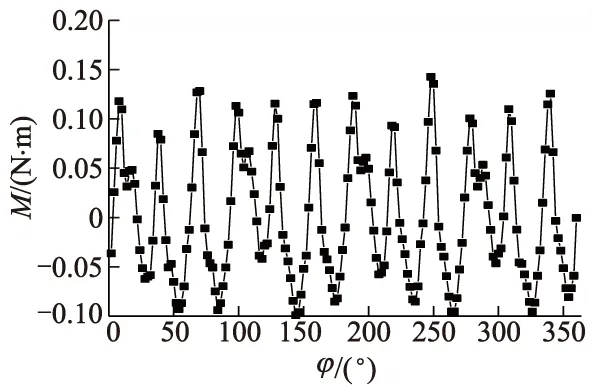
图9 新型轴流叶轮转动角度与扭矩关系

动静盘阀是调制脉冲射流的关键部件,在初期室内试验中发现盘阀间隙是影响脉冲性能的关键参数.图10为不同盘阀间隙下非对称脉冲射流装置单孔出口处平均压力和速度的变化.

图10 不同间隙下动盘阀转动角度与出口压力和速度关系曲线

由图10可以看出,装置出口处形成了周期性的二次正态波动.随着盘阀间隙减小,单孔出口速度增加,速度幅值增大.在动静盘阀间隙为1 mm时,最大脉冲速度达到63.89 m/s,相比盘阀间隙为5 mm时提高34.28%,脉冲幅值达到1.08 MPa.可以得出,较小盘阀间隙下,脉冲射流装置可以大幅提高井底流场的瞬时射流力度,有效改变井底流场结构,最大程度降低压持效应.

图11为1 mm间隙下单个水力脉冲周期内出口速度云图,红圈代表动盘阀通道出口,序号1—5代表装置出口的5个孔.

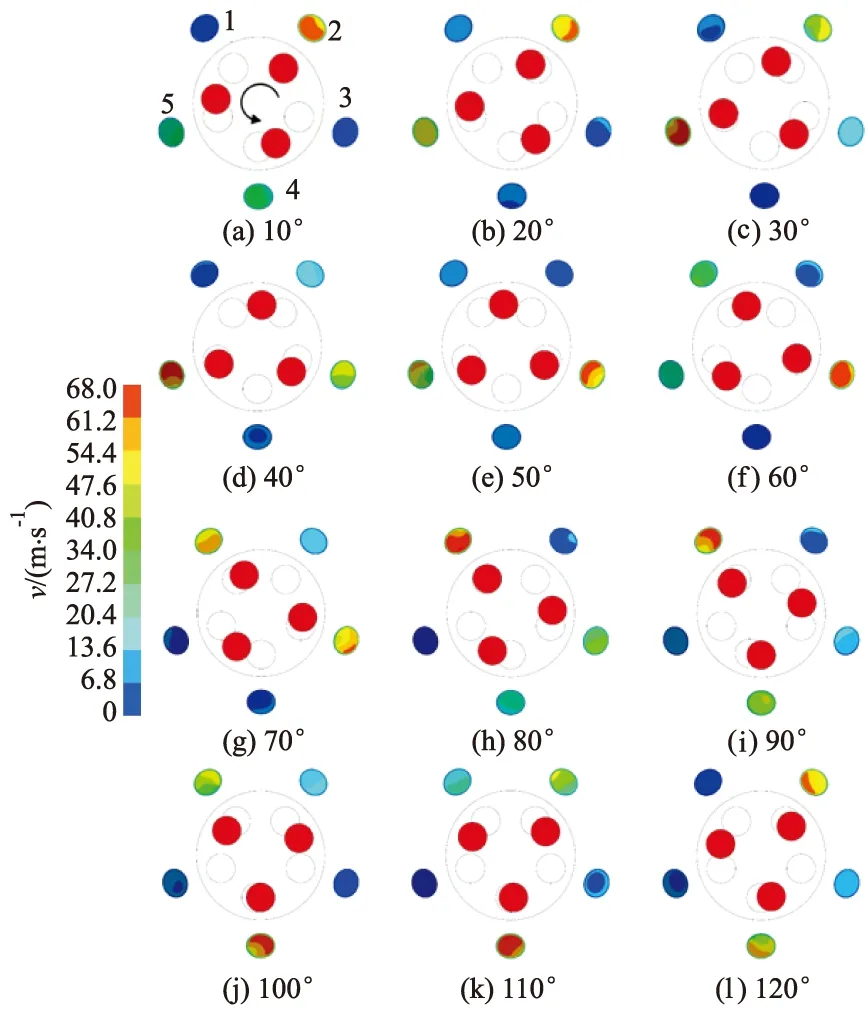
图11 单个水力脉冲周期内出口处速度分布

从图11中可以看出,当动盘阀通道与静盘阀孔口未完全契合时,出口处平均速度处于较低值.当动盘阀孔口与静盘阀孔口由未完全契合状态到完全契合状态,出口处平均速度由低值达到最大值.在10°的时,动静盘阀完全契合下,孔2达到最大瞬时射流力度,孔1与孔3速度处于低值区间.同理,当单孔达到最大瞬时射流力度时,相邻两孔处于出口速度低值区间.在一个水力脉冲周期内,孔口达到最大瞬时射流力度的顺序是2-5-3-1-4-2的循环.可以得出,装置出口处可以形成周期性的强不对称性脉冲射流.

3.2.2 不同盘阀间隙下能量损失特性

图12为不同盘间隙下不同类型熵产分布规律,从图中可以得出,随着间隙的减小,动盘阀和静盘阀内的各类型熵产呈现逐渐增大的趋势,增长率也呈现出上升趋势.

图12 不同盘阀间隙下3种熵产分布

不同类型的熵产中,由于脉动速度引起的熵产增长量高于时均速度引起的熵产和壁面熵产,动静盘阀段不稳定流动是能量损失的主要原因.静盘阀区域内脉动速度引起的熵产和壁面熵产远高于动盘阀区域,静盘阀区域存在更大的速度梯度变化.结合图5可以发现,盘阀间隙相比于水动力叶轮段对装置的能量损失影响更大.间隙越小能量损失越大,脉冲幅值越大,脉冲效果越好.

图13为动盘阀和静盘阀间内部流动特性.

图13 动静盘阀速度流线

从图13中可以看出,水流冲击动盘阀壁面出现回流现象,在动盘阀进口处存在明显的旋涡.盘阀间隙内流动更为紊乱,存在着冲击和旋涡造成的速度梯度变化.图13b处高速水流冲击静盘阀上壁面后,以较高速度向四周扩散,其中一部分流体冲击侧壁面产生旋涡,另一部分水流在中心处相互碰撞产生较紊乱的旋涡,如图13c所示.侧壁面附近旋涡和中心处旋涡对动盘阀通道与静盘阀未契合的孔口2,5产生较大的影响,在孔口处存在图13d所示的旋涡.未完全契合孔口3,4主要受到非均匀入流影响,高速水流与低速水流发生剪切,在出口管道内水流产生脉动速度.完全契合孔口1受到间隙内紊乱流动较小.进一步分析可得,随着动静盘阀间隙减小,静盘阀上壁面受到更大的水流冲击力,壁面切应力和旋涡强度随之增加,壁面熵产和脉动速度引起的熵产增加.