考虑时序特征提取与双重注意力融合的TCN 超短期负荷预测

周思思，李 勇，郭钇秀，乔学博，梅玉杰，邓 威

（1.湖南大学电气与信息工程学院，湖南省 长沙市 410082；2.南方电网科学研究院有限责任公司，广东省 广州市 510663；3.国网湖南省电力有限公司电力科学研究院，湖南省 长沙市 410007）

0 引言

超短期负荷预测是指对未来5 min 到1 h 的电力负荷大小进行预测，精确的超短期负荷预测是电网实时调度和安全预警的基础，对于电网的安全稳定和经济运行具有重要支撑作用。台区超短期负荷预测以台区配电变压器负荷为预测对象，预测结果有助于提前预警台区配电变压器的安全运行状态，辨识配电网薄弱环节［1-3］。

现有的负荷预测方法可分为统计学方法和机器学习方法两大类［4］。常见的统计学方法有时间序列分析法［5-6］和回归分析法［7-8］，这类方法原理简单、计算速度快，但非线性拟合能力差，对负荷数据要求高。机器学习算法因其能捕捉复杂的非线性关系，成为当前的研究热点。在电力大数据背景下，传统的机器学习算法［9-12］缺少对时序数据时间相关性的考虑，对于处理具有多特征输入或长期依赖关系的大规模负荷数据仍较困难［13-14］。深度学习是近年来兴起的机器学习算法，典型方法有以长短期记忆网络［15］、门控循环单元［16］为代表的循环神经网络，卷积神经网络［17］，深度置信网络［18］以及图神经网络［4］。然而，单一的神经网络模型无差别对待输入特征及其时序差异，制约了负荷预测精度的提高。

除了在预测模型上的创新，部分负荷预测研究也着重于挖掘负荷的规律性，关注于利用分解算法将负荷序列分解为多个分量序列，把高度非线性的非平稳负荷序列预测问题转化为多个相对平稳的负荷序列预测问题。常用的负荷分解方法有傅里叶分解［19-20］、小波变换［21］以及模态分解［7，22-24］。负荷特征分量从复杂的负荷序列中提取了关键的规律信息，然而，上述研究均将分解得到的负荷特征分量序列作为预测对象，尚未有研究将分解得到的负荷特征分量作为预测模型的输入特征。

配电网超短期负荷预测的预测对象大多是系统级负荷，较少关注以台区为单位的负荷预测。在超短期负荷预测模型选择方面，已有研究由采用统计学模型［1，25-28］逐步发展为采用深度学习模型［2，15，29-32］进行预测。部分研究也关注于负荷序列分解方法［31，33-35］，挖掘负荷的内蕴规律。由于台区负荷量测数据与外部特征数据间存在粒度不匹配的问题，即在外部特征数据的相邻两个采集点所在的时间范围内，多个负荷数据采集点仅对应一个外部特征数据采集点。因此，无法直接挖掘粗粒度外部特征与细粒度负荷变化规律的相关性。此外，相较于系统级负荷，台区负荷具有数量级小、波动性大、随机性高的特点，加大了超短期负荷预测的难度。

为进一步提高台区超短期负荷预测精度，本文提出一种基于Prophet 和双重多头自注意力（dual multi-head self-attention，DMHSA）-时间卷积网络（temporal convolutional network，TCN）的台区超短期负荷预测框架，从输入特征构建和预测模型优化两个角度实现对台区负荷的全面挖掘预测。在输入特征构建方面，挖掘负荷的内蕴规律性，提取多时间尺度时序特征作为负荷预测模型的输入特征，可有效避免引入气象因素等外部特征造成的输入数据粒度不匹配问题。在预测模型优化方面，特征多头自注意力（feature multi-head self-attention,FMHSA）机制量化输入特征变量间的关联关系，时序多头自注意力（temporal multi-head self-attention,TMHSA）机制捕获时序信息的依赖关系，从而增强重要特征变量与关键时间步的信息表达。引入的DMHSA机制有效地解决了传统神经网络无差别对待输入特征和时间步的问题。

1 基于Prophet 和DMHSA-TCN 的台区超短期负荷预测框架

本文所提基于Prophet 和DMHSA-TCN 的台区超短期负荷预测框架如图1 所示，预测对象为台区视在功率，具体步骤如下。

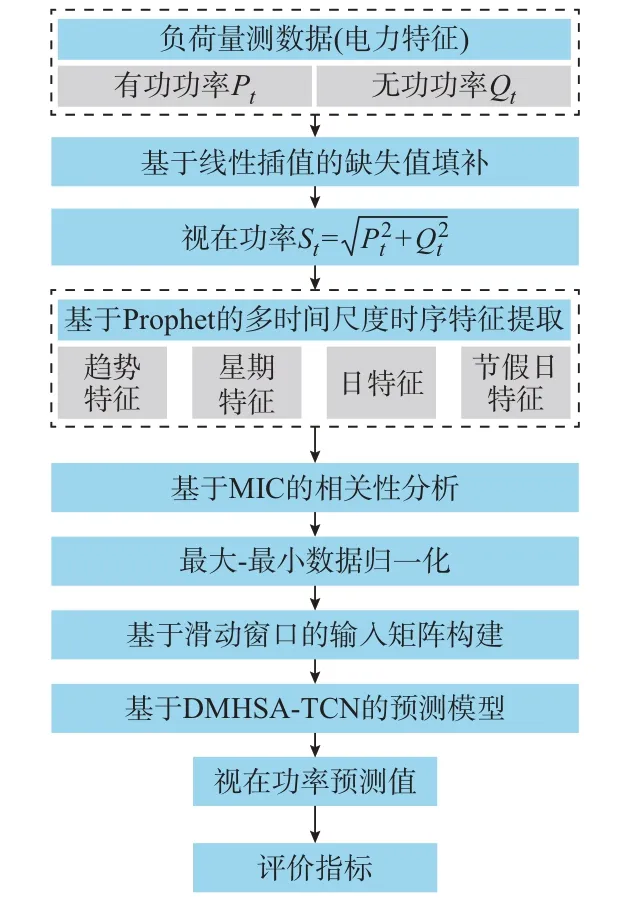
图1 基于Prophet 和DMHSA-TCN 的超短期负荷预测框架Fig.1 Ultra-short-term load forecasting framework based on Prophet and DMHSA-TCN

1）采用线性插值法填补台区负荷量测数据中的缺失值，并根据有功、无功功率量测数据计算台区视在功率值。

2）采用Prophet 提取台区视在功率序列中隐含的多时间尺度时序特征，包括趋势特征、星期特征、日特征和节假日特征。

3）基于最大信息系数（maximum information coefficient，MIC），量化视在功率与电力、时序特征之间的相关性，选择强相关性特征作为预测模型的输入特征。

4）对输入特征进行最大-最小归一化处理，采用滑动窗口的方式构建输入特征矩阵与对应的输出，形成输入-输出对数据集，并划分训练集与测试集。

5）将训练集输入DMHSA-TCN 模型中进行训练，优化模型参数。将测试集输入训练完成的DMHSA-TCN 模型，得到视在功率预测值。基于视在功率真实值与预测值，计算相关预测结果评价指标。

2 基于Prophet 的预测模型输入特征提取

2.1 Prophet 时序特征提取

Prophet 是由Taylor 等人开发的一款集成时间序列分解和预测功能的时序分析工具，其基本框架见附录A 图A1。Prophet 通过拟合历史时序数据的变化规律，将原始时间序列分解为趋势、周期、节假日和误差分量。同时，Prophet 还能对趋势、周期、节假日分量进行预测，通过整合分量预测结果，从而得到原始时间序列的预测值。目前，Prophet 在时间序列分解［36］和时间序列预测［37-38］方面已有广泛的应用，本文使用Prophet 的时序分解功能。不同于传统的趋势-周期时序分解模型［39-40］，Prophet 能实现快速迭代优化，提取时间序列中的多种周期性和节假日效应，具有出色的灵活性和鲁棒性。

台区负荷是复杂的时间序列，在不同时间尺度上会呈现不同的周期性规律，在节假日等特殊状况下还可能会出现破坏趋势与周期性规律的波动性。因此，本文采用Prophet 自动检测台区负荷数据的趋势变化、周期变化和节假日效应，为负荷预测模型的输入提供更具规律性的特征样本，降低数据复杂度，提升负荷用电特点的可解释性。对于任意台区负荷序列L(t)，Prophet 可将其分解为多种规律项和误差项的组合，具体如式（1）所示。

式中：g(t)为趋势项，用于拟合负荷序列中的趋势变化；s(t)为周期项，表征负荷序列中的周期性变化（如年、月、星期、日周期性）；h(t)为节假日项，反映不规律节假日效应的影响；εt为误差项，表示模型无法容纳的特异性变化，一般认为服从高斯分布。

在Prophet 中，趋势项g(t)有两种拟合模型，分别为基于线性回归的分段模型和基于逻辑回归的饱和增长模型。本文选用基于线性回归的分段模型拟合台区负荷的趋势变化规律，其表达式如下：

式中：k为台区负荷的基本增长率；δ为负荷增长率调整向量；α(t)为指示函数；θj(t)为α(t)在第j个突变点处的取值；sj(j=1，2，…，S)为台区负荷序列中第j个突变点所在时刻；M为偏移量参数；γ为突变点处的平滑处理偏移量；台区负荷在t时刻的增长率即为k+αT(t)δ。因此，Prophet 分解得到的趋势项考虑了台区负荷序列突变造成的增长率变化。

对于周期项s(t)，Prophet 采用傅里叶级数来拟合台区负荷序列中的多种周期性，其表达式如下：

式中：P为周期，以天为单位；β为平滑系数aγ和bγ的集合，其满足正态分布；N为平滑系数aγ或bγ的个数；γ为平滑系数的序号。

对于节假日项h(t)，Prophet 假设节假日中每一天都是相互独立的，其表达式如下：

式中：Z(t)为回归矩阵；Dl为第l个节假日过去和未来日期的集合，l=1，2，…，L，共有L天；κ为节假日对应的先验变化参数，满足正态分布；v为节假日的影响力，v越大，表示该节假日的影响力越大。本文中使用的Prophet 参数均为默认参数。

考虑到现有预测方法中使用的外部特征如气象数据的粒度低于负荷数据的粒度，且由于台区气象数据量测装置不齐备或者出现故障等原因，气象数据中存在大量的缺失值，上述两种情况均需采取相应的填充方法使不同粒度的数据相匹配。为解决上述问题，考虑到外部因素对负荷的影响本就隐含在负荷自身变化规律之中，本文充分利用台区负荷量测数据，包括台区有功功率Pt和无功功率Qt，根据式（9）计算相应的视在功率St，采用Prophet 提取台区视在功率序列中多时间尺度时序特征，包括趋势特征、星期特征、日特征以及节假日特征。

图2 为1 号台区的时序特征提取结果，从原始负荷曲线St可以看出，该台区负荷波动较大，随机性较强。趋势特征分量曲线Tt反映该台区2021 年6 月至8 月的负荷整体呈波动上升趋势，在8 月上旬末达到峰值，这是由于夏季空调负荷增大引起的。节假日特征分量曲线Ht反映了节假日对该台区负荷的影响。相较于趋势特征分量，节假日特征分量的值较小，说明端午节（2021 年6 月12 日至14 日）对该台区的影响较小。星期特征分量曲线Wt反映该台区的星期用电特性。日特征分量曲线Dt反映该台区的日用电特性，在06：00 和14：00 时刻左右达到一天中的用电高峰。相较于日特征分量，星期特征分量值较小，反映了此台区没有明显的星期周期性。值得注意的是，除趋势特征以外的其他特征分量值均有正负值出现，其正负值反映了其他特征分量基于趋势特征的变化量，从而使总特征分量值逼近原始负荷值。2 号、3 号、4 号台区的时序提取结果分别见附录A 图A2、图A3 和图A4。综合分析4 个台区的时序提取结果可得，4 种时序特征在一定程度上反映台区负荷在不同时间尺度上的变化规律，因此，本文将其作为待选的预测模型输入特征。

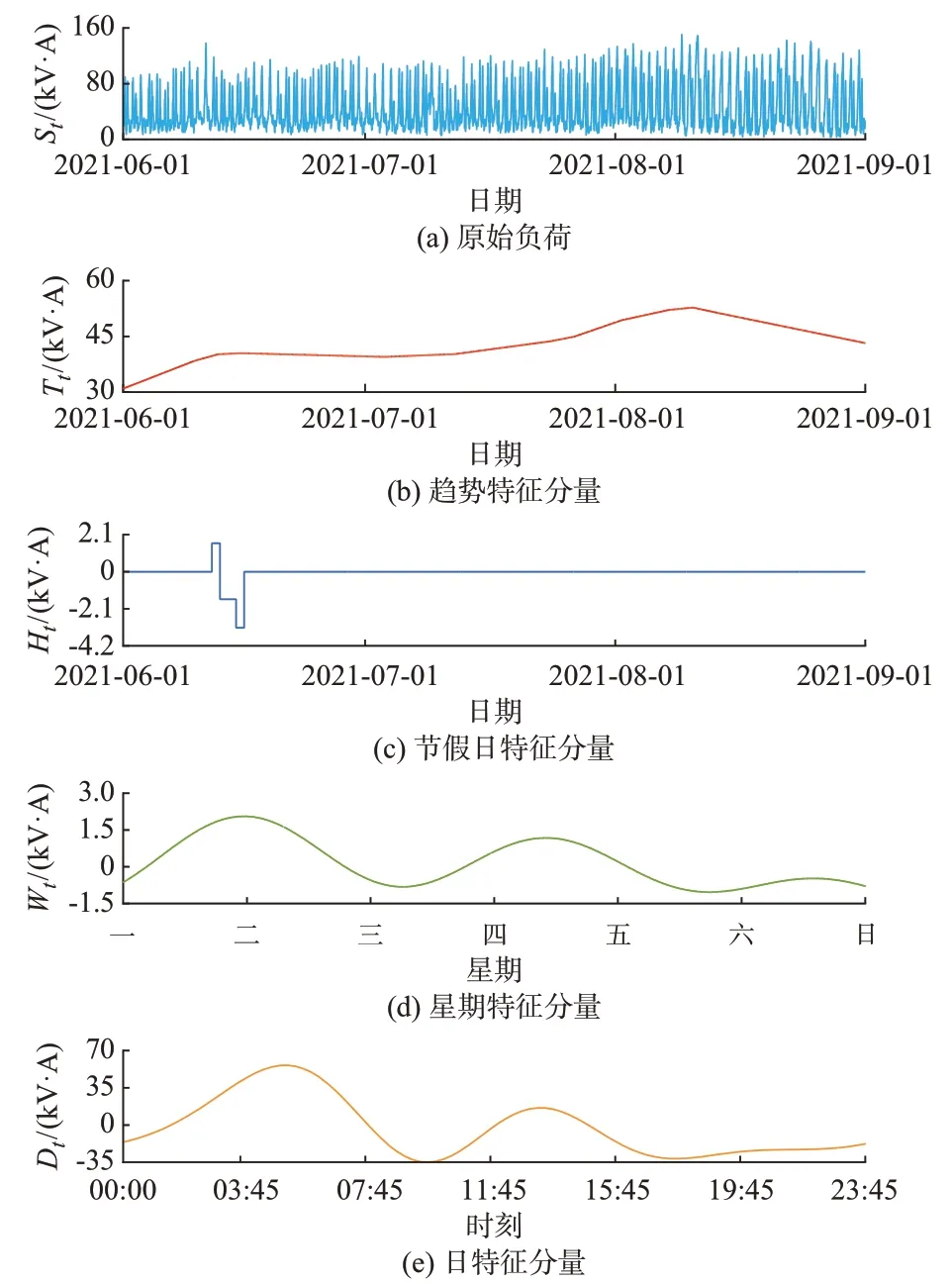
图2 1 号台区时序特征提取结果Fig.2 Temporal feature extraction results of transformer area 1

2.2 相关性分析

为量化特征分量序列与视在功率序列的相关程度，本文采用MIC 作为相关性分析方法，选择强相关特征作为预测模型的输入。MIC 能衡量两个变量间的线性和非线性相关性，克服了互信息对连续变量计算不便的缺点，具有公平性和广泛性。MIC值越接近1，表示两个变量间的关联性越强，MIC 的计算公式见附录A 式（A1）。本文选择0.3 为MIC的阈值，即认为MIC 取值范围小于0.3 时为弱相关，大于0.3 时为强相关［41-42］。

本文待选的输入特征包括视在功率、电力特征（有功功率、无功功率）和时序特征（趋势特征、星期特征、日特征、节假日特征）。台区视在功率与其他6 个特征的相关性分析结果如附录A 表A1 所示。对于1 号和3 号台区，采用MIC 筛选出的强相关特征为有功功率、无功功率、趋势特征和日特征。对于2 号和4 号台区，采用MIC 筛选出的强相关特征为有功功率、无功功率和趋势特征。在4 个台区中，电力特征均为强相关特征。对于时序特征，趋势特征在4 个台区上均为强相关特征；星期特征和节假日特征均为弱相关特征，因为相较于原始负荷值和趋势特征分量，这两种特征分量值较小，反映出的特征规律并不明显；日特征在1 号和3 号台区上为强相关特征，在2 号和4 号台区上为弱相关特征，这是由于1 号和3 号台区的日特征分量值相较于原始负荷值和趋势特征分量较大，而2 号和4 号台区的日特征分量值相较于原始负荷值和趋势特征分量较小造成的。

3 基于DMHSA-TCN 的负荷预测模型

本文所提DMHSA-TCN 负荷预测模型以TCN为基础模型，用以捕捉负荷和特征变量序列中的长期依赖关系。为提高TCN 的负荷预测精度，引入DMHSA 机制。在输入侧，引入FMHSA 机制多方面挖掘负荷与电力、时序特征变量的内在相关性，聚焦重要特征变量的影响。在输出侧，引入TMHSA机制多方面挖掘不同时间步间的内在相关性，突出关键时间步上的信息表达，在TCN 的基础上捕获更为灵活的长期依赖关系。

3.1 TCN 模型

TCN 是一种融合扩张因果卷积（dilated causal convolution，DCC）和残差连接（residual connection，RC）的神经网络模型，其网络架构如附录A 图A5 所示，由输入层、多个残差块和输出层堆叠构成。

因果卷积可有效避免传统卷积神经网络中由于卷积运算导致的未来信息泄露问题，其结构如附录A 图A6 所示。DCC 在因果卷积的基础上，通过增加过滤器大小K和扩张系数d，从而接受更广泛的输入信息，增大感受野。此外，DCC 中每层网络采用相同大小的过滤器，从而实现并行化计算处理，提高计算效率。DCC 的结构如附录A 图A7 所示，具体的计算公式为［43］：

式中：f(·)为过滤器函数；xT-di为从T时刻向过去平移di时刻对应的输入值。

除了调整上述过滤器大小和扩张系数，TCN 中还能通过增加层数来增大感受野。然而，层数过多的深度网络模型在训练时不稳定，易出现梯度消失现象。TCN 中的RC 结构允许上一层的误差直接传入下一层，能有效解决此问题。RC 由两个分支组成，第1 个分支对输入做变换，第2 个分支对输入做1×1 卷积处理，两个分支的输出结果相加，作为RC的最终输出。RC 的具体计算公式为：

式中：δ(·)为激活函数；G(·)表示DCC、权重规范化、激活函数、随机失活4 个部分的变换；Xh-1为残差块h-1 的输出；Xh为残差块h的输出。其中，激活函数采用具有良好收敛性的ReLU 函数，随机失活层用于正则化，防止深度网络出现过拟合问题。

综上，DCC 能并行捕捉台区负荷和特征变量序列中的长期依赖关系，RC 结构又能有效避免在负荷预测过程中出现梯度消失问题。此外，相较于循环神经网络和卷积神经网络，TCN 的参数更少、训练难度更低，需要的数据规模更小［44］。因此，本文采用TCN 为基础的负荷预测模型。

令输入的视在功率、强相关性电力特征变量以及时序特征变量构建大小为k×n的负荷特征矩阵X，共有k(1 ≤k≤7)个特征，滑动窗口的宽度为n(n≥1)。X可表示为：

式中：xm=[xm1，xm2，…，xmn](1 ≤m≤k)为输入特征m在n个时刻下的矩阵；xt=[x1t，x2t，…，xkt]T(1 ≤t≤n)为t时刻下k个输入特征的矩阵。

附录A 图A8 所示为本文采用的TCN 结构，将负荷特征矩阵X输入TCN 中，通过2 个残差块［45］计算，即可得到负荷预测输出Y，计算如下：

式中：X1为残差块1 的输出；X2为残差块2 的输出，即为负荷预测值；δ(·) 为激活函数；ym=[ym1，ym2，…，ymn](1 ≤m≤k)为输出特征m在n个时刻下的矩阵；yt=[y1t，y2t，…，ykt]T(1 ≤t≤n)为t时刻下k个输出特征的矩阵。

3.2 多头自注意力机制

TCN 能捕捉台区负荷与特征变量序列中的长期依赖关系，然而其忽略了输入信息中包含的特征差异和时序差异，在一定程度上会对台区负荷预测精度带来不利的影响。注意力机制是一种模拟人脑注意力的资源分配机制，可自适应为输入信息分配权重，实现以高权重聚焦重要信息，低权重忽略不相关信息［46-47］。

自注意力机制是一种特殊的注意力机制，也称内注意力，能表征输入序列内部不同位置间的相关性并分配权重。如附录A 图A9 所示，多头自注意力对多组自注意力的并行计算结果进行拼接，捕捉多种相关性，从而获得更全面的依赖关系［48］。

3.2.1 基于FMHSA-TCN 的负荷预测模型

为了得到负荷特征滑窗矩阵中多种输入特征变量间的关联关系，采用FMHSA 机制量化权重，其结构如附录A 图A10 所示。将负荷特征矩阵X输入FMHSA 层中，得到FMHSA 权重αm，计算如下：

式中：Qm为查询矩阵；Km为键矩阵；Vm为值矩阵；WQm、WKm、WVm分别为将负荷特征滑窗矩阵X转换为查询、键、值矩阵对应的转换矩阵；MH(·)为多头自注意力函数，具体计算原理见附录A 式（A2）—式（A7）。

对负荷特征矩阵X赋权Dm，可得到负荷特征加权矩阵X′，其表达式如下：

式中：Dm为以αm中各元素为特征值的对角矩阵，即Dm=diag(α1，α2，…，αk)∈Rk×k。

将特征自注意力层的输出X′输入TCN 中，通过两个残差块计算，再通过扁平层将TCN 层的输出矩阵一维化，即可得到负荷预测输出Y′。

式中：上标“′”表示采用FMHSA-TCN 负荷预测模型对应的变量，FMHSA-TCN 负荷预测模型中考虑了多种输入特征变量间的差异。

3.2.2 基于TMHSA-TCN 的负荷预测模型

为了得到TCN 层输出矩阵Y中多个时间步间的依赖关系，采用TMHSA 机制量化权重，其结构如附录A 图A11 所示。

将TCN 的输出Y输入TMHSA 层中，得到TMHSA 权重λt，计算如下：

式中：Qt为查询矩阵；Kt为键矩阵；Vt为值矩阵；WQt、WKt、WVt分别为将TCN 的输出矩阵Y转换为查询、键、值矩阵对应的转换矩阵。

按照吸收液和闪烁液的不同配比，配制10个本底样品，在同一台液闪谱仪中测量后，分别向本底样品中加入1mL的标准源，记录源重，然后放入同一台液闪谱仪中再次测量。

对TCN 的输出Y赋权Dt，即可得到时间步加权矩阵，计算如下：

式中：Dt为以λt中各元素为特征值的对角矩阵，即Dt=diag(λ1，λ2，…，λn)∈Rn×n。

相比于直接使用TCN，TMHSA-TCN 负荷预测模型中考虑了多个时间步间的差异。

3.3 DMHSA-TCN 预测模型

通过将上述特征和TMHSA 机制引入TCN中，组合FMHSA-TCN 和TMHSA-TCN 负荷预测模型，本文所提DMHSA-TCN 负荷预测模型结构如图3 所示，主要包括输入层、FMHSA 层、TCN 层、TMHSA 层、扁平层和全连接层。

具体预测流程为：首先，将由台区视在功率、电力特征、时序特征构成的负荷特征矩阵X输入FMHSA 层中，量化台区视在功率与电力、时序特征间的关联性，为不同的输入特征赋权，获得特征加权矩阵X′；然后，将特征加权矩阵X′输入TCN 层中，捕获加权特征间的长期依赖关系，获得输出矩阵X″；在此基础上，将TCN 层的输出矩阵X″输入TMHSA 层中，挖掘不同时间步间的内在相关性，为不同的时间步赋权，获得时间步加权矩阵X‴。最后，通过扁平层将多维时间步加权矩阵X‴压缩为一维矩阵X4，通过全连接层综合上述各层信息，输出视在功率预测值，计算如下：

式中：WD∈Rkn×1为全连接层权重。

4 算例分析

4.1 算例概况

4.2 数据预处理

为保证预测模型的训练效果，本文采用线性插值法填补原始负荷数据中的缺失值。若原始负荷数据中出现单点缺点值（仅某一时刻的值缺失），使用前一时刻和后一时刻的数据平均值代替此时刻的缺失数据；若原始负荷数据中出现连续缺失值，对于每一时刻的缺失值，使用与该时刻相距最近、非缺失的两个历史相同时刻的负荷平均值来代替。为消除不同输入特征中存在的量纲差异，采用式（30）对数据进行最大-最小归一化。

式中：x和x*∈[0，1]分别为归一化前、后的值；xmax和xmin分别为原始数据中的最大、最小值。

采用滑动窗口的方式构建预测模型的输入和输出，即输入为指定滑动窗口宽度的特征矩阵，输出为某一时刻的视在功率，滑动窗口的滑动步长为1。划分所构建输入-输出对中的80%为训练集，用于训练预测模型；20%用作测试集，用于评估预测模型性能。值得说明的是，若台区的供电范围发生变化，通过选择滑动窗口的初始时刻，即可过滤掉台区在原供电范围下的历史数据，不会影响后续的预测工作。

4.3 模型参数与评价指标

综合考虑预测精度和计算时间，预测模型的训练批尺寸设为16，迭代次数为500，模型中各层参数设置见附录A 表A2。采用Nadam 优化算法对预测模型其他参数进行寻优，学习率为0.001。Nadam 算法由Adam 算法和Nesterov 加速梯度算法结合，给予学习率一定的约束，提高预测模型的自适应性［49］。预测模型的损失函数使用均方误差（MSE）LMSE函数，其计算公式如下：

式中：S为样本个数；ys为样本s的负荷实际值；y^s为负荷预测值。

为多方位评估模型的预测能力，本文采用拟合优度R2、均方根误差（RMSE）eRMSE、平均绝对误差（MAE）eMAE、对称平均绝对百分比误差（symmetric mean absolute percent error，SMAPE）eSMAPE这4 种评价指标，其计算公式如下：

4.4 滑窗宽度对模型性能的影响

滑动窗口宽度决定了用多长时间范围的历史特征数据进行预测，对预测精度和效率有一定的影响。相同样本数量下，滑动窗口宽度过短会导致输入包含的特征信息过少而遗漏关键信息，不利于预测模型的学习和训练；然而，滑动窗口宽度过长会导致用于模型训练的输入数据量增加，模型的训练时间变长、复杂度变高。为选择最优的滑动窗口宽度，本文为预测模型设置不同的滑窗宽度W=1，2，4，8，16，32（单位滑窗宽度为15 min），输入特征仅为视在功率，在4 个台区上的整体预测误差见附录A 图A12，计算时间见表A3。考虑到不同台区视在功率间的数值差异，采用eSMAPE衡量预测精度，采用计算时间衡量预测效率。

从附录A 图A12 可以看出，当滑窗宽度为4 时，即使用待预测时刻前1 h 的历史特征作为预测模型输入，4 个台区上的整体预测误差数值最小。从表A3 可以看出，预测模型的计算时间随滑窗宽度的增大而增加。综合考虑预测精度和预测效率，本文选择的滑窗宽度为4，相比于滑窗宽度为1 的预测模型，其以牺牲10.503%的时间换取低31.658%的预测误差；相比于滑窗宽度为2 的预测模型，其以牺牲5.294%的时间换取低25.390%的预测误差；相比于滑窗宽度为8、16、32 的预测模型，其在预测精度和效率上均具有优势。

4.5 特征选择对模型性能的影响

为探究输入特征对模型预测精度的影响，本文设置4 种预测模型输入特征选择方案，如附录A 表A4 所示。设输入特征为X=[x1，x2，…，xk]，其中x1为视在功率，x2为有功功率，x3为无功功率，x4为趋势特征变量，x5为星期特征变量，x6为日特征变量，x7为节假日特征变量。结合相关性分析结果，各台区在方案1 下选择的输入特征均为x1，在方案2 下选择的输入特征均为x1至x3，在方案3 下选择的输入特征均为x1至x7，在方案4 下选择的输入特征如附录A 表A5 所示。

采用上述4 种特征选择方案为预测模型筛选的输入特征，在4 个台区上的整体预测误差如附录A图A13 所示。采取方案1 选择的特征，即仅使用视在功率作为预测模型的输入，在4 个台区上的平均误差最大，为5.589%。采取方案2 选择的特征，即使用视在功率和全部电力特征作为预测模型的输入，在4 个台区上的平均误差为4.436%，相比于方案1，预测误差降低了20.630%，验证了本文使用电力特征的有效性。采取方案3 选择的特征，即使用视在功率和全部电力、时序特征作为预测模型的输入，在4 个台区上的平均误差为4.048%，相比于方案2，误差降低了8.747%，验证了本文使用Prophet提取得到的时序特征的有效性。

采用方案4 选择的特征作为预测模型的输入，在4 个台区上的平均预测误差最小，为3.674%。相较于选择全部电力、时序特征的方案3，预测误差降低了9.239%，验证了本文使用MIC 相关性分析方法筛选输入特征的有效性。

4.6 消融实验

为验证本文所提预测模型DMHSA-TCN 中各部分的有效性，对该模型进行消融实验，设置的4 种对比模型分别为TCN、FMHSA-TCN、TMHSATCN 和DMHSA-TCN。 其中，TCN、FMHSATCN、TMHSA-TCN 的结构分别在附录A 图A8、图A10、图A11 的基础上添加全连接层为模型的最后一层，输出预测结果。

为选择最优的多头自注意力头数，考虑到预测模型的复杂度，DMHSA-TCN 的FMHSA 层和TMHSA 层设置不同的注意力头数，注意力头数的选择范围为[1，5]。不同特征、时序注意力头数组合下4 个台区的整体预测误差如附录A 表A6 所示。当FMHSA 头数为3、TMHSA 头数为2 时，预测误差最小，与未使用多头自注意力时的预测误差相比减小64.859%。值得注意的是，并非所有使用特征/TMHSA 的预测模型都比使用单头自注意力的预测模型的预测效果好，使用前需对比选择。

在消融实验中，本文使用的DMHSA-TCN 预测模型中的特征/TMHSA 头数分别为3 和2，FMHSA-TCN 预测模型中的FMHSA 头数为3，TMHSA 头数为2。附录A 图A14 为对比模型在4 个台区测试集中最后一天的负荷真实值与预测值的曲线图，表1 为各模型在测试集上的预测误差。

从4 个台区的整体预测结果中可以看出，FMHSA-TCN 和TMHSA-TCN 的预测精度均高于TCN。相较于TCN，FMHSA-TCN 的预测拟合优度平均提升了13.773%，预测误差eRMSE、eMAE与eSMAPE平均降低了50.014%、57.002% 与60.084%；TMHSA-TCN 的预测拟合优度平均提升了14.352%，预测误差eRMSE、eMAE与eSMAPE平均降低了50.373%、59.532% 与 64.018%，表明了引用FMHSA 和TMHSA 可以有效提升台区负荷预测拟合优度与精度。

其中，DMHSA-TCN 在所有台区的预测结果评价指标中表现最优。 相较于FMHSA-TCN，DMHSA-TCN 的预测拟合优度平均提升了2.182%，预测误差eRMSE、eMAE与eSMAPE平均降低了23.112%、21.596% 与25.799%。相较于TMHSATCN，DMHSA-TCN 的预测拟合优度平均提升了1.654%，预测误差eRMSE、eMAE与eSMAPE平均降低了23.154%、18.375% 与 18.399%。 结果验证了DMHSA-TCN 中FMHSA 和TMHSA 组合的有效性。相较于单独使用特征或TMHSA，组合使用给预测模型性能带来的提升效果更大。

4.7 多种预测模型对比

为进一步说明本文所提模型在台区超短期负荷预测中的优势，选择两种传统机器学习模型支持向量机（SVM）、极限梯度提升（XGBOOST）和4 种深度学习模型长短期记忆网络（下文简称LSTM）、双向长短期记忆网络（下文简称BiLSTM）以及添加特征、时序双重多头自注意力的DMHSA-LSTM、DMHSA-BiLSTM 作为对比模型。其中，SVM、XGBOOST、LSTM 和BiLSTM 的具体参数设置如附录A 表A7 所示。DMHSA-LSTM 和DMHSABiLSTM 中LSTM 层、BiLSTM 层与LSTM 和BiLSTM 单独模型具有相同的参数设置，添加的FMHSA 头数为3，TMHSA 头数为2。所有对比模型的迭代次数、训练批尺寸、优化算法、损失函数等其他参数设置均与DMHSA-TCN 相同。

图4 为各模型在测试集中最后一天的负荷真实值与预测值的曲线图，表2 为各模型在测试集上的预测误差。相比于两种传统机器学习模型，DMHSA-TCN 在预测精度方面具有优势。具体地，相比于SVM，DMHSA-TCN 在4 个台区上的预测拟合优度平均提升了18.724%，预测误差eRMSE、eMAE与eSMAPE平均降低了 63.986%、70.541% 与74.353%。相比于XGBOOST，DMHSA-TCN 在4 个台区上的预测拟合优度平均提升了13.780%，预测误差eRMSE、eMAE与eSMAPE平均降低了58.281%、64.103% 与69.127%。值得说明的是，DMHSATCN 在计算时间上与传统机器学习模型相比并没有优势。因此，在某些不过分注重预测精度的场景下，仍可考虑使用传统机器学习模型进行负荷预测，而本文所提DMHSA-TCN 预测模型更关注于预测精度的提高。

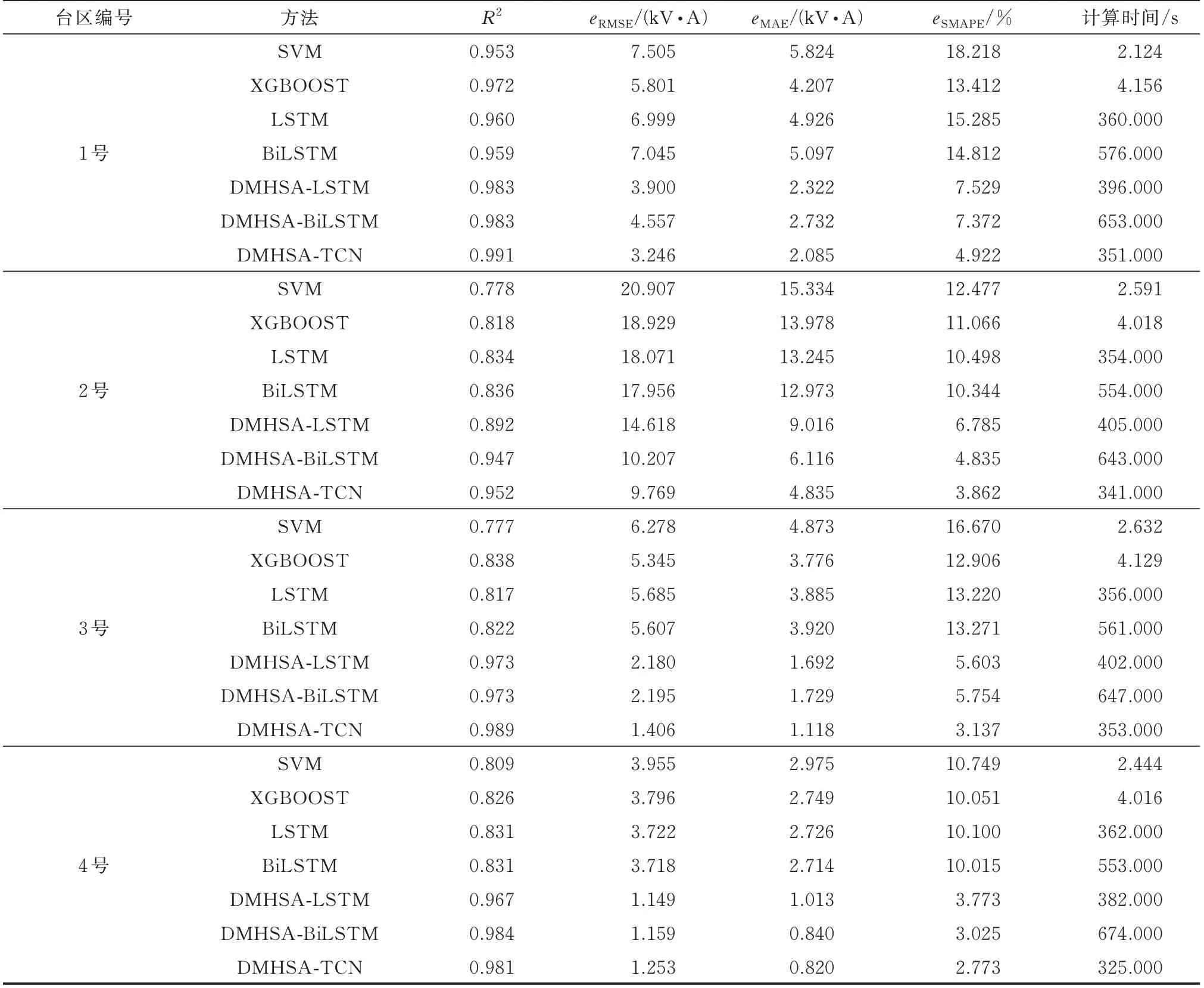
表2 不同模型的预测误差Table 2 Forecasting errors of different models

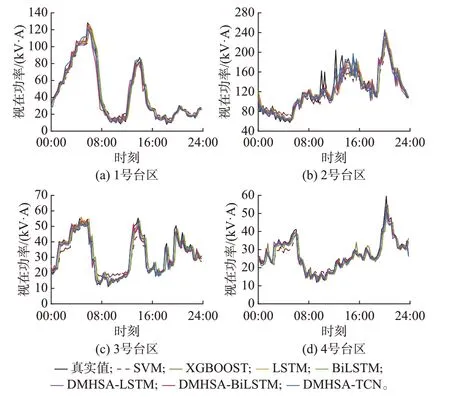
图4 不同模型的预测结果Fig.4 Forecasting results of different models

相比于4 种深度学习模型，DMHSA-TCN 在预测精度和预测效率两方面均具有优势。具体地，相比于LSTM，DMHSA-TCN 预测拟合优度平均提升了14.120%，预测误差eRMSE、eMAE与eSMAPE平均降低了60.292%、65.578%与69.956%，计算时间减少4.309%。相比于BiLSTM，DMHSA-TCN 预测拟合优度平均提升了13.895%，预测误差eRMSE、eMAE与eSMAPE平均降低了60.186%、65.772% 与69.527%，计算时间减少38.954%。相比于DMHSA-LSTM，DMHSA-TCN 预测拟合优度平均提升了2.658%，预测误差eRMSE、eMAE与eSMAPE平均降低了19.098%、27.389%与37.056%，计算时间减少13.569%。相比于DMHSA-BiLSTM，DMHSA-TCN 预测拟合优度平均提升了0.670%，预测误差eRMSE、eMAE与eSMAPE平均降低了15.224%、20.587% 与26.792%，计算时间减少47.609%。

基于上述分析可得，本文所提DMHSA-TCN预测模型的预测能力强于DMHSA-LSTM 和DMHSA-BiLSTM，说明TCN 和双重多头自注意力的组合优于LSTM、BiLSTM 和双重多头自注意力的组合。这是因为相比于循环神经网络LSTM 和BiLSTM，TCN 能实现并行计算，且能避免出现梯度消失问题，能更好地挖掘负荷与特征序列间存在的依赖关系。此外，DMHSA-LSTM 和DMHSABiLSTM 的预测能力强于LSTM 和BiLSTM，同时也验证了特征、时序双重自注意力的有效性。

附录A 图A15（a）所示为1 号台区测试集中的一个输入样本数据，特征维度为5，包括视在功率、有功功率、无功功率、趋势特征和日特征，时间步维度为4，即时间范围为1 h。附录A 图A15（b）所示为FMHSA 层的输出，可以看出多头自注意力机制为负荷特征输入矩阵中不同的特征赋予了不同的权重。附录A 图A15（c）所示为TCN 层的输出，可以看出TCN 挖掘负荷特征间隐含的长期依赖关系，筛选重要特征。附录A 图A15（d）所示为TMHSA 层的输出，可以看出多头自注意力机制为TCN 层输出矩阵中不同的时间步赋予了不同的权重。本文所使用的特征/时序双重多头注意力机制，从特征和时间步两个维度为负荷特征矩阵赋权，以突出关键信息的影响，提高TCN 的预测性能。

5 结语

本文提出一种面向配电网超短期负荷预测的DMHSA-TCN 混合模型，有效提高了台区超短期负荷预测精度，相关结论如下：

1）充分利用台区负荷量测数据，采用Prophet 提取负荷序列中的时序特征，挖掘台区不同时间尺度上的用电特性。将提取得到的强相关时序特征作为所提预测模型的输入特征，有利于预测模型的学习与训练。

2）DMHSA-TCN 预测模型由TCN、FMHSA、TMHSA 三大主要部分构成。双重多头自注意力能够挖掘多个输入特征、多个时间步之间的内部关联性并赋以相应权重，提高TCN 时序预测能力。消融实验结果验证了DMHSA-TCN 预测模型通过设定合理的注意力层与注意力头数，能有效提升台区负荷预测效果。

3）与传统机器学习预测模型相比，所提DMHSA-TCN 预测模型具有更高的预测精度；与深度学习预测模型相比较，所提DMHSA-TCN 预测模型在台区超短期负荷预测精度和预测效率上均具有一定的优势。

本文在4 个不同用电特性的典型台区上验证了所提预测框架的有效性，后续可以研究台区聚类方法，进行多时间尺度预测工作，进一步提高预测模型的通用性。在此基础上，可开展台区配电变压器重过载预警工作。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。