考虑定功率-定关断角方式的交直流协调三级电压控制方法

颜 伟，张紫薇，胡显文，李程昊，张 迪

（1.输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆市 400044；2.国网河南省电力公司电力科学研究院，河南省 郑州市 450052）

0 引言

近年来，随着中国新能源发电和新型间歇负荷功率占比的增加，电网潮流波动加剧，基于电网换相换流器的高压直流（line commuted converter based high voltage direct current，LCC-HVDC）输电工程中，交流滤波器、并联电容器和换流变压器分接开关（统称为换流站离散调压设备）的频繁动作问题对电力系统的运行安全造成了严重威胁［1-5］。例如，2018年4 月新疆哈密换流站换流变压器因分接开关频繁动作而造成失火事故。换流站离散调压设备的动作原因包括直流传输功率的变化和交流系统潮流的波动。前者会影响换流器消耗无功和谐波含量，相应设备的投切是必须的；而后者会引起换流母线电压的变化进而影响换流器消耗无功，为满足直流系统就地无功平衡的独立控制要求，换流站离散调压设备也会动作。为便于区分，本文将交流系统潮流波动引起的换流站离散调压设备动作称为额外动作。在当前实际工程中，换流站的电压无功控制并未纳入交流系统的自动电压控制（automatic voltage control，AVC）中，交直流系统无功不协调引起的换流站离散设备频繁动作问题加剧。因此，如何处理特高压直流输电的运行约束，解决交直流系统的电压无功协调控制问题是中国目前发展特高压交直流混联电网亟须解决的现实课题［6-8］。

三级电压控制作为AVC 中的一个关键环节，以静态无功优化［9-10］作为决策依据。现有研究中，已有学者对交直流系统的静态无功优化［11-15］进行了研究。文献［11-12］所提方法中均包含交直流系统总网损最小化目标，能够有效降低整体网损，但均认为交流系统和换流站内的所有调压设备都能统一进行优化，不符合实际工程中直流系统的独立控制要求［3，16］。文献［13-15］所建模型均考虑了离散调压设备，但可能会存在收敛性及计算速度问题，难以满足AVC 的实时控制要求。文献［17］提出一种考虑换流站独立控制约束的交直流系统静态无功优化方法。该方法以交流系统的连续调压设备为控制对象来优化全网的无功潮流，实现交流系统AVC 对直流系统的协调，从而有效避免了换流站离散调压设备的额外动作问题。文献［3］提出一种考虑直流离散调压设备动作频次的高压直流输电系统改进控制策略，通过对直流运行效率的极少量牺牲，换取直流系统离散调压设备动作频次的显著降低，提高了直流工程的运行可靠性。然而，上述文献所提方法均难以适应送-受端定功率-定关断角（constant powerconstant extinction angle，CP-CEA）控制方式下送-受端的耦合。

目前，CP-CEA 方式是工程上实际应用的典型控制方式之一，其受端换流变压器采用电压控制模式［16-18］。尽管与送-受端定功率-定电压（constant power-constant voltage，CP-CV）方式相比，CP-CEA方式下受端换流变压器分接开关动作次数有所减少［19-21］，但在交直流系统AVC 不协调的情况下，也可能产生更突出的额外动作问题。因为在CP-CEA方式下，送-受端换流站的电压、无功相互耦合，受端交流系统潮流波动导致的换流母线电压变化会同时影响送-受端换流器的消耗无功及直流电压，由此可能导致两端换流站离散调压设备的额外动作［22］。

本文通过分析CP-CEA 方式下送-受端之间的耦合关系，结合交流滤波器/并联电容器及换流变压器分接开关的实际工程控制策略，从实时运行的角度，提出了一种考虑CP-CEA 方式的交直流协调三级电压控制方法。所提方法在遵循交流系统协调直流系统原则的同时，保持了直流系统的独立控制特点，不仅有效抑制了换流站离散设备的额外动作，而且能够在一定程度上降低电网的有功损耗。

1 CP-CEA 方式下的直流系统独立控制

1.1 直流系统及其特性方程

图1 所示为一个直流输电系统的简化示意图。图中：下标1 对应直流系统送端换流站，2 对应受端换流站；Qdexc为交直流系统之间的交换无功；Qd为换流器的消耗无功；UH和Ud分别为换流母线电压和直流电压；kdT为换流变压器阀侧变比；Id为直流电流；Rd为直流传输线路等效电阻；QcrD为换流站内交流滤波器/并联电容器的总补偿无功；α和γ分别为送、受端换流器的触发角和关断角；AC1和AC2分别代表和送-受端换流器互联的两个交流系统。

图1 直流输电系统简化示意图Fig.1 Simplified schematic diagram of DC transmission system

对图1 所示直流系统，送-受端换流器的特性方程［23］可表示如下：

式中：k取1、2 分别表示送、受端换流站；θk为换流器控制角（送端为α、受端为γ）；kb，k为换流站每极六脉动换流器数；kp，k为换流器运行极数；η为换流器换相系数，取η=0.995；Xc，k为换相电抗；Sd，k、Pd，k、Qd，k分别为换流变压器并网侧视在功率、有功功率和无功功率。

1.2 CP-CEA 方式下送-受端状态变化的耦合关系

1）送端潮流扰动的影响。CP-CEA 方式下，直流送端采用定功率控制方式。分析特性方程式（1）可知，当送端交流系统潮流变化导致换流母线电压UH，1波动时，变比kdT，1不变，可以通过α的调节保持直流功率Pd，1以及直流电压Ud，1和电流Id都不变。分析式（2）可知，当Pd，1和Id不变时，Sd，1和Qd，1会随着UH，1的波动而变化。由此可得出以下结论：在CP-CEA 方式下，送端交流系统的潮流变化只影响送端换流器的控制角和消耗无功，不影响受端状态。也就是说，送端的潮流扰动对受端没有耦合作用，这种解耦特点与CP-CV 方式相同。

2）受端潮流扰动的影响。CP-CEA 方式下，直流受端采用定关断角控制方式。同样，分析式（1）可知，此时kdT，2和γ不变，UH，2的波动会导致Ud，2和Id都发生变化。再分析式（2）可知，Ud，2和Id的变化会导致Sd，2和Qd，2变化。当然，直流线路的有功损耗也会随着Id的变化而变化。

另外，当Ud，2和Id变化时，为满足Pd，1的恒定控制要求，送端通过调整α使Ud，1在一定范围内变动。当kdT，1不变时，分析式（1）和式（2）可知，Ud，1、Id和α的变化会进一步导致UH，1和Qd，1的变化。

图2 CP-CEA 方式的控制逻辑Fig.2 Control logic of CP-CEA mode

基于上述分析可以得出如下结论：CP-CEA 控制方式下，受端的潮流波动不仅影响受端的直流电压和换流器消耗无功，而且影响送端的控制角、消耗无功以及直流电压、直流电流和直流线路有功损耗。因而，在受端潮流波动时，送-受端和直流网络状态之间具有强耦合关系，这与CP-CV 方式的解耦特点完全不同。本文主要研究受端的三级电压控制问题。至于送端，可以采用文献［17］方法，本文不考虑这一情况。

1.3 交流滤波器/并联电容器的投切策略

现有直流工程中，无论是送端还是受端，换流站内交流滤波器/并联电容器的投切都主要采用就地无功平衡的独立控制方式，要求其补偿无功的投切满足交换无功Qdexc的死区控制要求。具体策略如下：

式中：Ncrd为换流站内无功补偿装置的投入组数，-1 或+1 为投入或切除1 组交流滤波器/并联电容器；Qdz为交流滤波器/并联电容器的投切死区；Qdexc，ref为交直流系统之间交换无功的参考值，对于不同直流输电工程或同一直流输电工程不同传输功率下，交换无功参考值不同，其值可根据具体直流输电工程的成套设计书确定。

以天中直流工程送端的哈密换流站与系统交换无功参考值的设计方案为例。如图3 所示，在直流功率小于2 100 MW 时，交换无功参考值为0 Mvar，直流功率大于2 100 MW 时，逐渐增加交换无功参考值至1 100 Mvar。

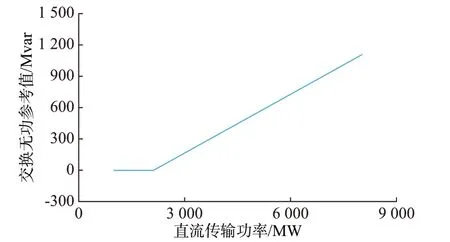
图3 哈密换流站交流电网注入直流系统无功参考值曲线Fig.3 Reference value curve of reactive power injected into DC system from AC grid of Hami converter station of China

1.4 换流变压器分接开关的调整策略

CP-CEA 方式下，送端和受端换流变压器分接开关的控制方式不同。对送端，分接开关的调节需要保证换流器控制角不越限；对受端，换流变压器分接开关采用电压控制方式，使直流电压或换流变压器阀侧绕组空载电压回到允许的范围内。本文假设其中分接开关的控制目标为直流电压。一旦越限，则需要进行变压器的升降挡位操作。

总体而言，换流站内部的交流滤波器/并联电容器和换流变压器分接开关都遵循“越限”动作原则。由于其离散调压设备属性，日动作次数约束、工作寿命限制、停电检修可能会带来经济损失等原因，都要求其不能频繁动作。因此，在实际工程中，交流系统潮流的正常波动应尽量通过控制角和直流电压的变化来抑制，尽可能避免换流站离散调压设备的额外动作。若交流系统的AVC 不考虑直流系统的独立控制特点，则可能带来严重的额外动作问题。

2 考虑CP-CEA 方式的交直流协调三级电压控制模型及算法

本文以三级电压控制周期内源-荷-换流站功率以及离散设备保持其初始运行状态不变为基本假设，在常规交流系统三级电压控制模型的基础上，通过增加直流线路的有功损耗目标，以提升交直流系统整体经济性；通过增加送-受端换流站的特性方程及直流网络方程以考虑CP-CEA 方式下两侧换流站具有的耦合关系；通过增加送-受端换流关口无功的控制死区约束、直流电压安全约束、触发角安全运行约束，以保持换流站的独立控制，使得换流站内离散调压设备不参与交直流互联电网的无功电压调节，从而实现交流系统对直流系统的协调，避免交直流不协调导致换流站离散调压设备出现额外投切。下文介绍模型的具体目标和约束条件。

2.1 目标函数

本文以交直流系统整体有功损耗最小为优化目标：

式中：PG，r、PL，s和Pd，k分别为发电机r、负荷s和换流站k的有功功率；sP，k表示换流器运行工况，换流器运行于整流工况时sP，k=1，换流器运行于逆变工况时sP，k=-1；NG、NL、ND分别为发电机（调相机）、负荷和换流站节点的个数。

2.2 约束条件

1）交直流系统的节点功率平衡方程约束：

其中

式中：ΔPi、ΔQi分别为节点i的有功、无功功率误差；PG，i、PL，i、Pd，i分别为节点i所连的发电机、负荷和换流器的有功功率；QG，i、Qcr，i、QL，i和Qd，i分别为节点i所连的发电机、无功补偿装置（含换流站的交流滤波器/并联电容器）、负荷和换流器的无功功率；sP，i、sQ，i表示节点i所连换流站情况，节点i与整流站相连时sP，i=sQ，i=1，节点i与逆变站相连时sP，i=-1、sQ，i=1，节点i未与换流站相连时sQ，i=sP，i=0；j∈i表示节点j与节点i直接相连，并包括j=i的情况；Gij和Bij分别为节点导纳矩阵对应元素Yij的实部和虚部，即Yij=Gij+jBij；θij=θi-θj，为i、j两节点电压之间的相角差；SAC为交流节点的集合；Ui为节点i电压幅值；Ncr，i、QcrN，i、UcrN，i分别为节点i处所连无功补偿装置投入组数、单组额定容量、额定电压；scr，i为节点i处所连无功补偿装置类型，当无功补偿装置为交流滤波器和并联电容器时scr，i=1，为并联电抗器时scr，i=-1；SCR为无功补偿节点的集合。

2）送-受端换流器特性方程约束（式（1）—式（4））。

3）直流网络方程约束：

4）节点电压幅值安全约束：

式中：下标min、max 分别表示变量的最小、最大值。

5）发电机无功出力上下限约束：

式中：SG为发电机节点的集合。

6）直流电流的安全运行约束：

7）送端直流电压的安全运行约束：

8）换流站离散调压设备的投切死区约束

a）送端换流器触发角的安全运行约束。CPCEA 控制方式下，触发角会随着受端换流母线电压的变化而变化。为避免送端换流变压器的额外动作，需要考虑触发角的安全运行约束。具体如下：

b）受端直流电压的安全运行约束。CP-CEA 控制方式下，受端直流电压会随着受端换流母线电压的变化而变化。为避免受端变压器的额外动作，需要考虑受端直流电压的安全运行约束。具体如下：

c）送-受端交换无功的控制死区约束。CPCEA 方式下，送-受端交换无功会随着受端换流母线电压的变化而变化，为避免两端交流滤波器/并联电容器的额外动作，需要考虑两端交换无功的控制死区约束。具体如下：

综上所述，本文模型由式（1）—式（18）构成，其中式（15）—式（17）对应换流站离散调压设备的“动作死区约束”。在直流系统保持其独立控制方式不变时，利用交流系统协调直流系统，若潮流状态满足上述约束，则换流站离散调压设备不动作，否则需要进行投切操作。本文控制变量仅考虑受端交流系统的连续控制变量（如发电机、调相机、静止无功补偿器、静止无功发生器等，本文假设已知其无功功率和电压的允许调节范围），模型是一个连续的非线性优化问题，可采用内点法［24］求解，本文借助IPOPT 求解器实现模型计算。

3 算例分析

3.1 基础数据

本文基于2 个修正的IEEE 39 节点标准算例系统构造了一个异步互联电网，两个交流子网之间有一回双极运行的直流输电系统，其结构见附录A 图A1。图中：左侧电网对应送端；右侧电网对应受端。整流站与左侧电网节点23 相连，逆变站与右侧电网节点14 相连。设虚构系统中的交直流系统基准容量SB=8 000 MV·A，交流基准电压UB=500 kV。直流系统基准电压UdB=800 kV，额定功率PdN=8 000 MW，额定电压UdN=±800 kV，直流线路电阻Rd=10.56 Ω。送-受端换流站具体配置参数见附录A 表A1。

假设虚构系统中的直流系统采用CP-CEA 控制方式，初始运行状态为：Pd，1=0.9 p.u.，γ=17°。其送端换流关口交直流系统交换无功的参考值跟随直流功率的变化而变化，可根据图3 曲线确定。当前直流传输功率下，Qdexc，ref，1=950 Mvar。受端采用“零无功交换”模式，Qdexc，ref，2=0 Mvar。

3.2 两种方式下受端换流变压器分接开关对应的控制范围对比分析

为对比分析相同交流潮流扰动对CP-CV 和CP-CEA 两种直流控制方式下受端换流变压器分接开关动作行为的影响，设计了如下仿真方案：

S1.1：直流系统采用CP-CV 控制方式，基于3.1节基础数据，并假设送端和受端换流变压器分接开关初始挡位分别为2 和-4，送端交流滤波器和并联电容器的初始投运组数nf10、nc10分别为11、1，受端交流滤波器和并联电容器的初始投运组数nf20、nc20分别为11、4。送-受端增投1 组并联电容器（用QC表示），采用交替迭代法确定算例系统的潮流状态。

S1.2：直流系统的控制方式改为CP-CEA 方式，其他条件同S1.1。

基于S1.1、S1.2 的仿真方案对比分析两种控制方式下增投1 组并联电容器前后的直流状态量，仿真结果如表1 所示。表中：Ud，20、Ud，2和γ0、γ分别为QC增投前、后的受端直流电压和关断角；Δqs为QC增投前后直流状态量的变化比例。

表1 两种控制方式的直流状态量比较Table 1 DC state quantity comparison of two control modes

表1 中的直流状态量，对CP-CV 方式为Ud，2，对CP-CEA 方式为γ。选择Ud，2和γ，是因为交流系统的潮流扰动会对这两个量产生直接影响，当其越限时会导致换流变压器的额外动作。

由表1 可知，投入1 组电容器，在CP-CV 方式下（对应S1.1），γ的变化量占其允许范围［17°，20°］的百分比为2.48%；而采用CP-CEA 方式时（对应S1.2），Ud，2的变化量占其允许范围［0.923 75，0.945 00］的百分比为2.35%。这说明，相同的交流系统潮流扰动对CP-CEA 方式的状态量影响更小，表明采用CP-CEA 方式更容易抑制换流变压器分接开关的额外动作。

3.3 考虑CP-CEA 方式的交直流协调三级电压控制方法优化效果分析

为验证本文所提方法在送-受端换流站离散调压设备无额外动作情况下的优化效果，设计如下仿真方案：

S2.1：采用本文所建模型（简称M1）进行优化计算，优化前的运行参数同S1.1；

S2.2：计算S2.1 优化前的初始潮流状态。

基于3.1 节基础数据和仿真方案S2.2 和S2.1 计算优化前后的状态量，结果如表2 所示。表中：Pac，loss为交流系统有功损耗；Pdc，loss为直流系统有功损耗；α为送端换流器触发角；Qdexc，1、Qdexc，2分别为送、受端交直流系统交换无功。

表2 方案S2.1 和S2.2 的计算结果Table 2 Calculation results of schemes S2.1 and S2.2

由表2 可知，触发角、受端直流电压、送受端换流关口的交换无功均未越限，即此时不存在换流站离散调压设备的额外动作问题。在这一情况下，优化前、后交流有功损耗分别为2 771.0、3 642.2 MW，本文所提优化方法使得交流网损降低了23.92%；优化前、后直流有功损耗分别为212.1、216.0 MW，本文所提优化方法使得直流降损率为1.81%。该结果表明，本文所提交直流系统协调三级电压控制优化方法在直流系统不存在额外动作问题时，能显著降低交直流系统有功损耗。

3.4 换流站离散调压设备投切死区约束的影响分析

为对比分析交直流不协调状态下交流滤波器/并联电容器和换流变压器分接开关的投切死区约束的影响，需调整其初始状态，使触发角、受端直流电压、两侧交直流系统交换无功尽可能接近极限值。因此，设置送端和受端换流变压器分接开关初始挡位分别为3 和-4。交流滤波器、并联电容器的初始投运组数分别为：nf10=11，nf20=11，nc10=1，nc20=4。

设计如下仿真方案以验证本文所提方法在送-受端换流站离散调压设备有额外动作情况下的优化效果：

S3.1：基于3.1 节基础数据及上述离散设备投运组数，计算优化前的初始潮流状态；

S3.2：采用模型M1 进行优化计算；

S3.3：采用CP-CEA 方式，在模型M1 的基础上，忽略送-受端交流滤波器/并联电容器和换流变压器分接开关的投切死区约束（式（15）—式（17）），构造修正模型M2，其他运行参数同S3.1。

基于3.1 节及上述基础数据和仿真方案S3.1、S3.2 和S3.3 进行交直流系统三级电压控制优化计算，结果如表3 所示。表中：Ploss为交直流系统总有功损耗。

表3 方案S3.1、S3.2 和S3.3 的优化结果Table 3 Optimization results of schemes S3.1, S3.2 and S3.3

由表3 可知，经方案S3.1 得到的初始潮流状态中，送端换流器触发角、换流关口交换无功均发生越限，此时，换流站离散调压设备存在额外动作问题，全系统有功损耗为3 858.3 MW。利用方案S3.2 和S3.3 分别对其进行三级电压控制优化计算，其损耗相比于S3.1 的初始潮流状态，分别降低了22.68%、24.66%。此时，相比于S3.2，S3.3 优化下的有功网损虽有小幅降低，但其多数站内离散调压设备均超出其死区约束。其中，送端换流器触发角超出其安全运行下限12.5°约23.53%，受端直流电压超出其安全运行上限0.945 p.u.约2.79%，表明送-受端换流变压器分接开关可能均需发生额外动作。同时，送端换流关口交换无功为598.02 Mvar，超过其控制死区［-215，215］Mvar，即送端无功补偿装置可能出现额外投切问题。而方案S3.2 由于考虑了送-受端交流滤波器/并联电容器和换流变压器分接开关的投切死区约束，其优化后的各状态量均未超出其限制范围，即两侧离散调压设备均不发生额外动作。

3.5 基于河南省网实际数据的交直流系统三级电压控制应用

为验证本文方法的有效性，选取了2022 年8 月7 日06：10 时刻的河南省调主网状态估计数据。从中得到以下统计结果：全网总负荷为40 822.58 MW，包含978 个节点、147 个发电厂、444 台变压器、1 583 条支路。落地河南的有天中和青豫两个直流工程。其中，天中直流的控制方式为CP-CEA。算例以天中直流为仿真对象。

天中直流参数配置见附录A 表A1。当前时段送端直流功率Pd，1=5 481.95 MW，关断角γ=17°。由图3 交换无功参考值曲线可知，Qdexc，ref，1=630 Mvar。送端的换流变压器分接开关挡位为10，送端交流滤波器投运组数nf1=10，并联电容器投运组数nc1=0；受端的换流变压器分接开关挡位为10，交流滤波器投运组数nf2=6，并联电容器投运组数nc2=0。

为验证本文所提方法在实际工程中应用的有效性，设计如下仿真方案：

S4.1：基于3.1 节及上述基础数据，计算优化前的初始潮流状态；

S4.2：基于S4.1 算例数据，采用模型M1 进行优化计算；

S4.3：基于S4.1 算例数据，采用模型M2 进行优化计算。

基于河南省网实际数据和仿真方案S4.1、S4.2和S4.3 进行计算，结果如表4 所示。

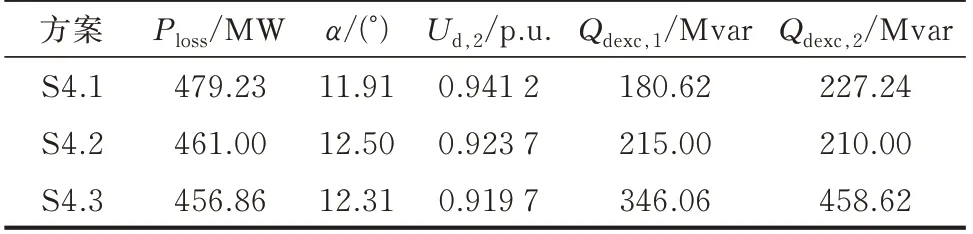
表4 方案S4.1、S4.2 和S4.3 的优化结果Table 4 Optimization results of schemes S4.1, S4.2 and S4.3

由表4 可知，相比于优化前初始潮流状态S4.1，利用模型M1、M2 进行三级电压控制优化，均可实现系统有功损耗的降低。其中，方案S4.2 由于增加了换流站离散调压设备的投切死区约束，设备均无额外动作风险；而方案S4.3 由于没有考虑到交流系统对直流系统的协调，其触发角、受端直流电压和两侧换流关口交换无功均出现越限现象，频繁动作风险增加。

综上所述，在CP-CEA 控制方式下，当直流系统存在额外动作问题时，若不考虑交流系统AVC 对直流系统的协调，不仅不能发挥换流变压器分接开关电压控制的优势，而且会导致更加突出的额外动作问题。而本文所建模型可以以牺牲少量网损为代价，抑制换流站离散调压设备的额外动作，进一步提升电力系统运行的安全性与经济性。

4 结语

本文提出一种考虑CP-CEA 方式的交直流协调三级电压控制方法。利用天中直流实际数据，以基于IEEE 39 节点修正系统构造的交直流电网和实际河南电网为例进行了仿真分析。相较于现有方法，本文通过关联换流器特性方程、直流网络方程以及直流线路有功损耗目标、送-受端换流站关口无功的控制死区约束、换流母线、直流电压及直流电流的安全约束，建立了交直流协调的三级电压控制新模型，有效提升了交直流系统的AVC 性能。仿真结果表明，本文所提交直流协调三级电压控制方法在换流站离散调压设备存在额外动作的情况下，可以通过牺牲少量网损有效抑制设备的额外动作；在换流站离散调压设备不存在额外动作的情况下，可以同时降低交、直流系统的有功损耗，在提升交直流系统的安全经济运行水平方面均存在优势，具有重要的工程应用价值。

本文所提方法需假设三级电压控制周期内源-荷-换流站功率以及离散设备保持初始运行状态不变，但随着新能源的接入，其随机性和间歇性会导致一天内的部分时段难以满足这一假设，可能导致三级电压控制实际控制效果不佳，如网损增加或电压质量下降。因此，如何考虑源-荷功率波动随机性与相关性背景下，三级电压控制对直流系统的电压无功协调作用有待进一步研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。