基于Lagrange插值法提高击实试验精度的方法研究

孙 露，丁继辉，马铁员

（1.辽宁生态工程职业学院，辽宁 沈阳 110000；2.河海大学农业科学与工程学院，江苏南京 210098；3.辽宁省水资源管理集团，辽宁 沈阳 110000）

0 引言

近年来，我国交通、水利等基础行业蓬勃发展，对河道堤防、道路路基等提出了更高的要求。有些公路、铁路或堤防在重载运输或经历几次汛期的情况下，会产生一定程度的变形和破坏。究其原因，主要是由于道路路基或河道堤防的压实度不够，承载能力低[1，2]。为了保证路基或堤防有足够的强度、稳定性和抵抗变形的能力，目前主要采用压实度指标来评价施工质量。

式中：K为压实度；ρd为现场实测压实干密度；ρdmax为同料源、同土样击实试验最大干密度。

ρdmax是影响现场土方压实度K的一个重要参数，其准确数值至关重要。目前ρdmax没有准确的求解解析式，主要通过击实试验结果估读曲线峰值确定，具有一定的B 类标准不确定度[3]。为减小误差，需要试验人员规范试验操作，并对击实数据进行合理分析，才能得到比较精确的ρdmax。

1 土方击实试验方案

根据GB/T 50123—2019《土工试验方法标准》，确定土方最大干密度和最优含水率的击实试验仪器分为重型和轻型两种，出于为堤防碾压施工提供基础技术参数的角度考虑，需要通过试验确定不同土场（料原地）的最大干密度。国内大多数交通、水利工程击实试验采用轻型击3 层击实（每层25 击）。辽河干流防洪提升工程击实试验土样采用的是施工十标段小高力房村排灌站附近的粉细砂黏土试样，击实试验采用轻型击实仪，仪器具体参数见表1。

通过击实试验得到干密度ρd～含水率ω的关系曲线，进而确定最大干密度ρdmax，干密度计算公式：

式中：ρ为湿密度。

为提高击实试验准确性，不少学者进行了深入系统的研究，如结合土样液塑限及平行对比试验，分析击实功对击实试验的影响及击实筒内涂抹润滑剂对土样最大干密度的影响等[4-6]。下文从试验用土、每层击实余土高度、Lagrange 数据处理方法等方面入手，分析提高室内击实试验确定土料最大干密度精确度的解决方法。

2 击实土样配制

为减少对土料最优含水率和最大干密度的影响，选择的土样尽量均匀、干净，不含腐殖物等杂质[7]。用四分法提取代表性风干土样，其中，大筒所需土样约50.0 kg，小筒所需土样约20.0 kg，土样用橡皮板木碾碾散。将碾散的土样拌匀并筛分，用台秤称取筛后土样测定风干含水率。根据塑限值预估最优含水率，制备以塑限值为中心的至少5个不同含水率土样组合，含水率差值不宜过大或过小，宜控制在2%左右。规范要求重型击实过20 mm 筛，轻型击实过5 mm 或20 mm 筛。含水率差值过大，数值点比较分散，峰值点不易确定；含水率差值过小，数值点比较密集，拟合计算可能遗漏某些关键点。关于土样质量的控制，一般小击实仪所需土样约2.5 kg，采用喷水设备对所取土样进行加湿处理，将土料拌匀并装入塑料袋内保湿，防止水分蒸发，高液限黏土要求静置时间大于24 h，低液限黏土可适当减少静置时间，但不得少于12 h。

3 土方击实余土高度的控制

击实试验完成后，常有一部分土样超出击实筒顶端，这部分“土”称为余土。GB/T 50123—2019规定干密度误差控制在允许范围内，前提是击实完成后，余土超出击实筒顶试样高度小于6 mm。若余土超过6 mm，筒内单位体积土击实功减小，土样没有达到击实标准，干密度数值减小；如土样高度低于击实筒顶端，击实筒内单位体积土样击实功增大，土样密实度增加，干密度数值增高。

松散状态下不同含水率土样的密实度不同，击实后体积缩减率也不同，规范建议轻型击实仪分3 层或5 层击实，每次击实装入土样量没有明确要求，若相邻两层装入土样量差别较大，则余土高度很难控制在规范要求的6 mm 范围内，影响土样最大干密度的精确度。为有效控制余土高度，建议采用“边击边算边测”控制方法：1）制备不同含水率土样前，先测定土样塑限，以塑限为中心设置土样含水率。按照平行对比试验思路，采用标准击实法制作一个对照样品，测出土体高度hck和总质量mck，测算各层装入筒内土样质量。2）装入对照样品1/3 的土样进行质量击实。轻型击实筒高度为116 mm，每层装入土样击实后高度尽量控制在39±1 mm，为保证击实质量，尽量使击实面平整。3）第1 层击实完成后，计算出击实后的土样高度h1与hck/3 的偏差△h1，以及计算装入第2 层土样的质量m2。以同样的方式计算第1 层、第2层击实后的土样高度h1+h2与2hck/3 的偏差△h2，计算装入第3 层土样的质量m3。2 层、3 层土样装入前，应对上一层已完成击实土样刨毛，以利于层间结合、保证击实质量。4）采用修土刀沿筒内壁削挖，扭动取下护筒，测余土高度（多个数据取平均值）。沿击实筒顶精心修平击实土样，拿下底板，擦净筒外壁，称量精度控制在1 g。推土器推出土样，并在土样中心处取两个一定量的土样测试其含水率，二者最大允许差值为±1%。

4 数据处理与分析

通常击实试验完成后，根据组内不同土样的含水率ω对应的干密度ρd，采用图解法画出对应曲线。这种方式得出的试验土样最大干密度与最优含水率受人为主观影响较大，具有较大的B 类不确定度，很难得出科学的土样最大干密度和最优含水率，给堤防、公路工程现场压实度施工带来不确定性。有的学者应用非线性最小二乘法进行曲线拟合，有的学者利用最小二乘法理论对数据定量分析，其准确性各有利弊。文中采用Lagrange 差值法进行三点二次和更高次插值拟合计算，对比分析试验土样最大干密度和最优含水率的测算准确性。Lagrange插值法数据分析的转化插值函数：

式中：ρ(ω)为含水率的函数，为插值拟合函数干密度；ωi，ωj为击实试验所测得的试样含水率值，且i≠j；ρi为对应含水率ωi的干密度值；n为试验次数，n=7。

根据插值点个数，用Matlab 计算式（3）的导函数，用牛顿迭代法求解多项式的根值，迭代方程：

式中：xk为k次迭代后的近似值；f(xk)，f′(xk)分别为当x=xk时的函数值和导函数值。

依据上述原理，尽量选择峰值左右的对称值，赋予适当初始含水率和迭代次数，确定土料最大干密度和最优含水率。

5 工程实例

以辽河干流防洪提升工程为例，采用Lagrange三点二次和高次插值方法进行曲线拟合计算，并求出试验土样的最优含水率和最大干密度，试验原始数据见表2。根据击实试验数据，用图解法绘制干密度～含水率曲线，见图1。

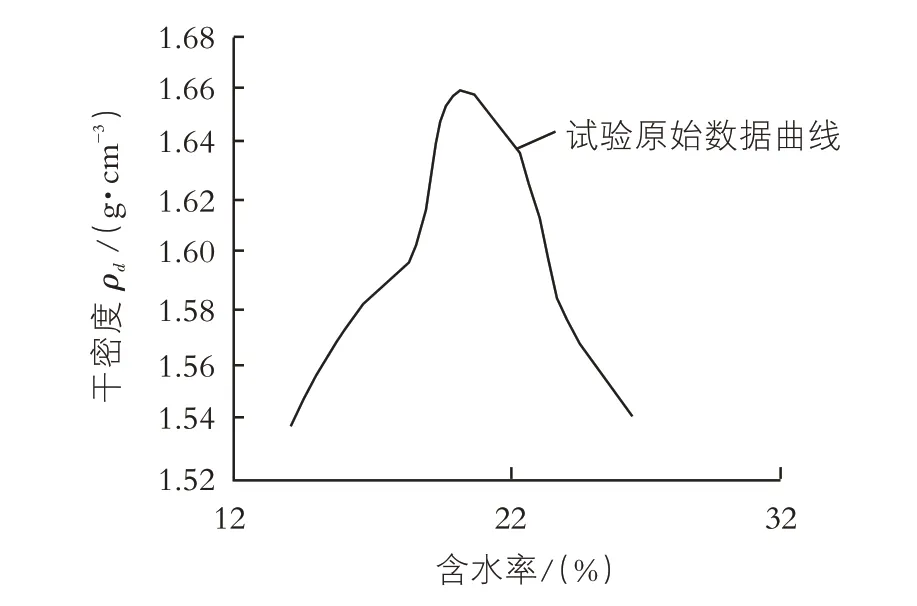
图1 干密度～含水率试验数据曲线

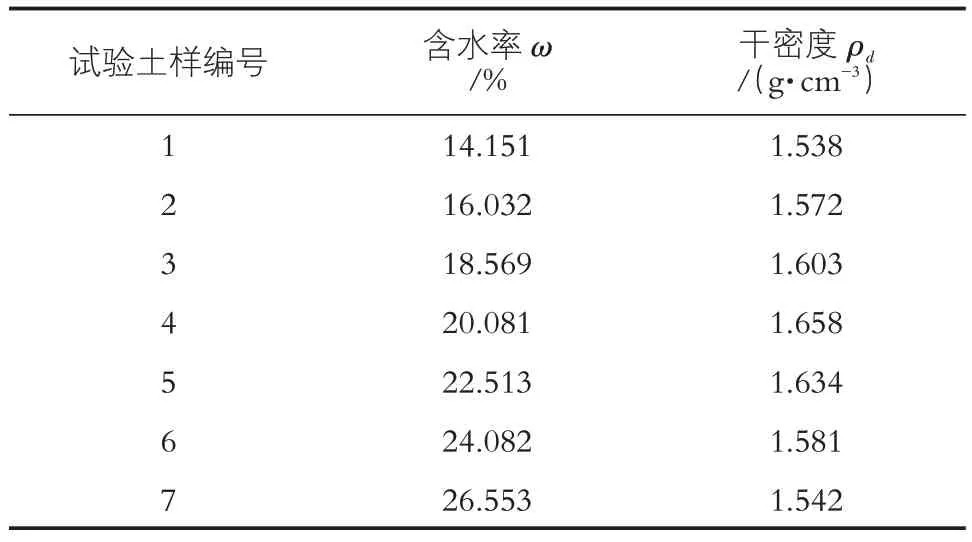
表2 土样含水率和干密度试验数据统计表

根据最接近曲线最大值位置点的原则，应用Lagrange 插值法对试验原始数据分别进行3 点（二次），5 点（二次、三次、四次），7 点（二次、三次、四次、五次、六次）多项式数据拟合计算。结果表明，3～5 号土样（3 点）插值点拟合曲线为向下开口的二次抛物线，与原始数据曲线重合度较高，见图2；2～6 号土样（5 点）插值点拟合曲线的顶点与原始数据曲线峰值也较为接近；1～7 号土样（7 点）拟合曲线的顶点与原始数据曲线峰值差值较大。

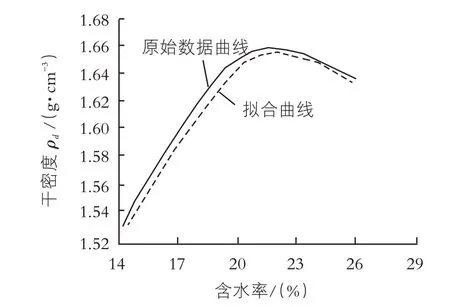
图2 试验数据曲线与拟合曲线（3 个点）对比

现用Lagrange 插值法分别对拟合度比较高的三点二次多项式和五点四次多项式求解最大值，用Matlab编写多项式求导程序，对多项式应用牛顿迭代法进行求根，并比较准确性。三点二次和五点四次项式最优含水率和最大干密度的计算结果：ω2=20.254%，(ρdmax)2=1.663 g/cm3；ω4=20.261%，(ρdmax)4=1.664 g/cm3。两种计算方法的最优含水率差值|△ω|=0.007%，最大干密度差值|△ρdmax|=0.001 g/cm3。二次多项式和四次多项式插值法所得结果相差无几，但从实际工程角度出发，建议采用三点二次多项式插值法。该方法计算相对简单，能提高试验数据分析效率，及时、高效地指导工程施工。同时，建议多项式拟合前尽量在峰值点附近取点，去除远离峰值点的数据，推算出相对准确的最大干密度和最优含水率，减小估读带来的人为误差。

6 结语

击实试验方法步骤虽较为简单，但在推求土样的最大干密度和最优含水率的过程中影响因素较多。其中，击实筒内“分层余土高度”是影响击实结果的一项重要因素。本文提出“边击边测边算”试验控制方法，在满足GB/T 50123—2019《土工试验方法标准》要求的情况下，可较为准确地推算出更接近真值的试验数据。但在此次试验过程中，对击实土样进行的修补是采用人工补土的方式，不同试验操作人员修补土样的干密度往往会产生一定的差异，试验的代表性有一定欠缺，因此，在后续类似试验工作中需要进行完善。

在推求土样的最大干密度过程中，本文采用数据法代替图解估读法，并采用Lagrange 多项式插值法进行数据拟合计算，该方法的关键是选择插值点，然而选取的插值点越多或拟合多项式次数越高，并不一定能提高试验准确性。在峰值点附近区间段选用三点二次插值就能够对该区间段内的曲线进行准确拟合，从而可精确求解最大干密度，此方法大大降低了对曲线进行高次拟合求解高次多项式的难度，提高了工作效率。然而，由于土的性质的复杂性和多变性，本文所选择的试验数据进行分析的结果并不能完全代表各类土样，故文中提到的公式仍需要在今后的试验过程中不断修改、完善，以待更好地适应工程建设的需要。