基于改进野狗优化算法的二维MUSIC声源定位研究

张蓝方，韦峻峰*，廖灿杰，倪童铮

（1. 广西民族大学电子信息学院，南宁 530000；2. 广西高校智慧无人系统与智能装备重点实验室，南宁 530000）

0 引言

声源定位技术在安防技术［1］、工业检测和军事探测［2］等领域应用广泛而备受关注。目前大体有三类声源定位的方法，分别是基于高分辨率谱估计的定向技术、基于到达时间差定位技术和基于最大输出功率的可控波束形成技术［3］。其中，基于特征分解的多重信号分类（multiple signal classificaion，MUSIC）算法［4］就属于基于高分辨率谱估计的定位方法，该算法实现了超分辨空间信号到达方向估计，其中最关键的一步为谱峰搜索，此步骤所采用的网格搜索法虽搜索精度高，但存在计算量巨大、实时性差的问题，难以较好地在工程中应用。近年来，已有学者尝试引入群智能算法来解决谱峰搜索过程复杂的问题。如将遗传算法［5］、鸡群优化算法［6］和改进蚁群算法［7］应用到MUSIC算法的谱峰搜索部分，它们虽然降低了算法的计算复杂度，也有较好的精度，但是这些算法仍然有着易陷入局部最优值、收敛速度慢的问题。

针对上述现象，本文介绍了野狗优化算法（dingo optimization algorithm，DOA）的改进版本，DOA是由Peraza-Vázquez等［8］在2021年提出的一种新颖的求解优化问题的仿生算法，具有较好的性能。Milenković 等［9］已成功将DOA应用于求解连续工程问题。为了使野狗算法性能更优，Almazán-Covarrubias等［10］在生存标准中加入了局部搜索程序，一定程度上提高了收敛速度和精度。但野狗优化算法仍存在优化的余地。

本文提出一种基于精英反向学习机制［11］和二次插值［12］的改进野狗优化算法（improved dingo optimization algorithm，IDOA）。一方面，在种群初始化和每一次种群迭代的过程中采用精英反向学习方法，避免了种群多样性差的问题；另一方面，引入二次插值方法，可以使算法得到更优的局部搜索性能。本文将改进野狗算法与传统二维MUSIC 算法的谱峰搜索部分相结合，使用IDOA 算法代替网格搜索法，以进一步降低计算复杂度，提高MUSIC 算法声源定位的实时性。

1 二维MUSIC算法

本文采用均匀线阵，假设有N个波长为λ的非相干窄带，以不同的方位角θ和俯仰角φ从远场入射到含M个阵元数的均匀线性阵上，入射信号源为S，将各阵元接收到的信号转化成矢量表达如下：

其中：X(t)为M× 1 维接收数据矢量，S(t)是N× 1 维信号源矢量，A(θ,φ)是M×N维阵列导向矢量，N(t)是M× 1维噪声矢量，且：

则阵列数据协方差矩阵为

其中：Rs是信号协方差矩阵，σ2I是噪声协方差矩阵。由于噪声子空间和信号子空间的正交特性，可将R矩阵进行奇异值分解得到噪声子空间UN和信号子空间US。则得出二维MUSIC 算法定义的空间谱函数为

对P(θ,φ)进行二维谱峰搜索，获得的谱峰所在的角度即为所要估计的信号波达方向角。

2 野狗算法改进

2.1 野狗算法

2.1.1 进攻策略

策略一：群体攻击。捕食者通常使用高度智能的狩猎技术，野狗通常单独捕食小猎物，如兔子；但当捕食大猎物，如袋鼠时，它们会成群结队。野狗能找到猎物的位置并将其包围，其行为如式子（5）所示：

策略二：迫害攻击。野狗通常捕猎小猎物，直到单独捕获为止。式子（6）模拟了野狗在单独捕获猎物时的轨迹：

策略三：清扫行为。野狗在栖息地随意行走时，发现腐肉可供食用的行为。式子（7）用于模拟此行为：

其中：(t+ 1) 是搜索代理的新位置（表示野狗的移动）；na是在［2,SizePop/2］的倒数中生成的随机整数；SizePop 是种群的规模。(t)是搜索代理（会攻击的野狗）的子集，其中φ⊂X，X是随机生成的野狗种群，(t)是当前的搜索代理，(t)是从上一次迭代中找到的最佳搜索代理，β1是在［-2，2］内均匀生成的随机数，这是一个改变野狗轨迹大小和感觉的比例因子，β2是在［-1，1］区间内均匀生成的随机数，(t)是选择的第1 个搜索代理，其中i≠r1。fitnessmax和fitnessmin分别是当前一代中最差和最好的适应度值，而fitness(i)是第i个野狗的当前适应度值。σ是由算法随机生成的二进制数，σ∈{ 0,1} 。

2.1.2 存活策略

澳大利亚野狗面临灭绝的危险，主要是因为非法狩猎。在DOA 算法中，野狗的存活率值由式子（8）提供：

其中：fitnessmax和fitnessmin分别是当前一代中最差和最好的适应度值，而fitness( )i是第i个搜索代理的当前适应度值。式子（9）应用于生存率值等于或小于0.3的搜索代理。

2.2 精英反向学习机制

对于群智能优化算法而言，初始种群的质量至关重要，种群质量的好坏会影响算法寻优能力的强弱，优质的初始种群能提升算法收敛速度以及得到更好的全局寻优能力。目前精英反向学习已被较好地应用于多种算法的改进。郭雨鑫等［13］引入EOBL改进哈里斯鹰算法，提高了算法的种群质量；何小龙等［14］将EOBL运用到鲸鱼优化算法的初始化种群和每次种群迭代中，增加了算法的种群多样性。另一方面，野狗算法的局部搜索能力还有进一步提升的空间。

而Peraza-Vázquez 等［8］的DOA 算法没有关于搜索空间的先验信息，初始化种群采取的方式是随机的，算法根据目前找到的最优野狗个体位置来更新其它个体位置，就可能会致使野狗种群多样性差、收敛速度慢的问题。若通过产生精英反向种群与初始种群一起竞争，选择出优秀个体作为下一代种群的方式引入先验信息，不仅可以扩大可行解的范围还保存了较优解，还提高了野狗种群多样性和质量。

定义1：精英反向解［15］。假设为当前种群内的精英个体，则精英个体的反向解定义为

其中：k为［0,1］区间上的随机数，lbj与ubj分别是动态边界的下界与上界。动态边界更易保存搜索经验，可增加算法的寻优速度。当越过边界变为非可行解时，则使用以下公式来重置：

2.3 二次插值方法

二次插值［12］的基本思想是在确定初始区间中，不断使用二次多项式去近似目标函数，随着区间的逐步缩小，二次多项式所得最优解与研究问题最优解之间的距离也逐渐缩短。此方法已经成功应用于多种算法的优化。如Guo等［16］结合二次插值策略改进正弦余弦算法；廖列法等［17］引入二次插值有效提升了天牛须搜索算法跳出局部最优的能力；高建瓴等［18］使用二次插值法改进包围策略，提高哈里斯鹰算法局部搜索能力。

本文提出将二次插值方法引入DOA算法中，利用这种方法提高DOA 算法的局部探索能力，提高算法的收敛速度和搜索精度。该方法的步骤如下：

假设三个个体，分别是X=(x1,x2,…,xd),Y=(y1,y2,…,yd),Z=(z1,z2,…,zd)，其中X、Y是随机选取的两个个体，Z具有最优适应度值，其中d是要求解问题的维度，适应度值分别是f(X)，f(Y)，f(Z)，使用二次插值法，通过式（12）生成新的个体使其与目前全局最优位置进行比对，择优作为新的全局最优位置。

其中：j= 1,2,…,d。新产生的个体Xˉ必然是二次曲线的极小值点。

2.4 改进算法IDOA的流程

结合了上述两个改进方法后，IDOA 算法的步骤为：

步骤1：使用精英反向学习策略对野狗种群进行初始化，随机生成N个野狗个体的位置，初始化研究问题维度dim、最大迭代次数tmax；

步骤2：根据目标函数计算每只野狗个体的适应度值，个体之间相互比较适应度值，记录当前种群的最优值个体的位置；

步骤3：通过策略一、二、三更新野狗的位置；

步骤4：再通过策略四计算野狗的存活率，当存活率值survival( )i≤0.3 时，通过式（9）更新存活率低的野狗；

步骤5：计算新野狗的适应度值，再次比较当前种群野狗个体之间的适应度值，找出全局最优值；

步骤6：引入二次插值策略，按照式（13）更新个体位置，计算并比较野狗个体的适应度值，更新最佳位置；

步骤7：判断算法是否达到终止条件（达到最大迭代次数），若达到，则跳转步骤7，否则转至步骤2；

步骤8：输出问题最优值。

3 实验仿真与结果分析

3.1 实验设计

在仿真实验中，式（4）的空间谱函数P(θ,φ)即为实验的目标函数。在高斯白噪声条件下进行，采用3阵元线性阵，角度搜索范围为（-90°，90°），阵元间距为半波长，种群规模为50，快拍数为512，信噪比SNR=10 dB，最大迭代次数tmax=100，传统网格的搜索步长Δ=0.1，信号源数为M=1。

由于MUSIC 算法的计算过程中消耗时间最多、计算量最大的部分是谱峰搜索部分，故本文提出将IDOA算法应用在MUSIC算法的谱峰搜索部分中。下面将通过仿真实验将改进后算法与传统二维MUSIC 算法在精度、时间上的表现进行对比。

3.2 实验结果

本文算法的谱峰搜索结果如图1所示，对比MUSIC 算法和改进后算法对不同方位入射角的波达方向估计结果参见表1。其中，设定入射角与算法搜索结果之间差值的绝对值即为下表所示的误差。

表1 不同方位的波达方向估计结果比较单位：（°）

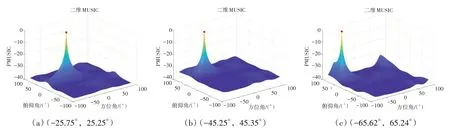
图1 不同方位的谱峰搜索图

传统MUSIC 算法与本文改进后算法的搜索结果分别用(θ1,φ1)和(θ2,φ2)表示，两种算法的测量误差分别用(Δθ1,Δφ1)和(Δθ2,Δφ2)表示。

由实验结果可知，本文算法与原算法相比搜索精度得到了提高，且搜索误差均在0.2°以内，搜索误差小，故使用IDOA 算法优化二维MUSIC算法的谱峰搜索部分是可行的、有效的。

下面进行时间复杂度分析。对于传统网格搜索方法，当以二维角度搜索时，主要是最大角度的维度与搜索步长影响着其时间复杂度，其公式如下：

其中：(θmax-θmin)和(φmax-φmin)分别代表着方位角和俯仰角的搜索范围；Δθ和Δφ分别是方位角与俯仰角的搜索步长。则通过式（14）可知传统网格搜索法的时间复杂度为O(3.24 × 106)。对于本文的IDOA 算法，其时间复杂度由种群数量与最大迭代次数tmax决定，则可知IDOA 算法的时间复杂度为O(5 × 103)。由此可以看出，使用IDOA 算法能够大大降低谱峰搜索的时间复杂度。比较MUSIC 算法和本文优化后算法进行谱峰搜索所用时间，结果如表2所示。

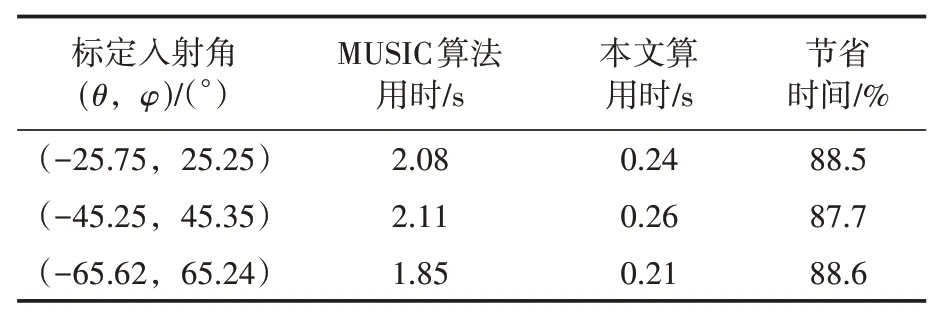
表2 谱峰搜索用时比较

由表2 数据可以看出，在此次仿真实验中，采用传统MUSIC 算法的用时基本在2 s 左右，而本文改进后算法搜索所耗费的时间基本稳定在0.2 s 左右，节省了约88%的运行时间，说明基于IDOA改进的MUSIC谱峰搜索方法，大大缩短了搜索时长，提高了谱峰搜索的速度，增强了算法的寻优能力。

4 结语

本文针对传统MUSIC 算法存在实时性差、计算复杂的缺陷，提出将改进野狗算法应用在传统二维MUSIC 算法的谱峰搜索部分。实验结果证明，改进后算法在提升原算法的定位精度的同时，还降低了计算复杂度，减少了计算量与搜索时长，改进后算法的整体性能更优，在实际生活中能够有更广阔的应用前景。本文已经初步验证了改进野狗算法对于提升声源定位性能的有效性，今后的工作方向主要是扩展改进野狗优化算法的应用领域。