新体制光学遥感卫星变转速环扫控制方法
2023-09-22奚瑞辰岳程斐曹喜滨
奚瑞辰,吴 凡,岳程斐,曹喜滨
(1. 哈尔滨工业大学航天学院,哈尔滨 150001;2. 哈尔滨工业大学(深圳)空间科学与应用技术研究院,深圳 518055)
0 引 言
微小卫星技术为低成本、快响应对地遥感提供了有效的解决方案[1]。为了能够在微小卫星平台上实现超宽覆盖光学成像的同时,保证较高的地面分辨率,作为一种新的成像体制,近年来提出了基于圆锥扫描的新体制超宽覆盖光学遥感卫星(亦即“光学环扫成像卫星”)的概念:通过整星绕对地轴自旋,带动倾斜安装的面阵光学相机在地面形成环扫条带,从而实现超宽覆盖成像[2-3]。文献[4-5]针对光学环扫成像卫星的不同应用场景,设计了快旋模式、慢旋模式和变转速环扫模式。其中,快旋模式条带拼接重叠区域小,减少了图像数据量,但降低了光学动态传函,影响了图像质量[6];慢旋模式提高了光学动态传函,但图像数据量大大增加,对数据处理和数传系统提出较高要求。前两种模式下卫星绕对地轴匀速自旋,对姿态控制能力要求不高。而变转速环扫模式则综合了前两种模式的优点,在一个环扫周期内,相机开机期间慢旋以提高成像质量,相机关机期间变转速快速环扫,从而有利于减小条带拼接重叠区域,减少图像数据量,但是对卫星的姿态控制提出较高要求。然而,文献[4]只给出了变转速环扫的开环控制方法,显然无法满足在有扰动和参数不确定性条件下的姿态稳定控制要求。因此,本文将针对新体制光学环扫成像卫星,设计控制策略,在实现变转速环扫模式的同时,确保相机开机期间的自旋相位角和自旋角速度的稳定性。
(w,z)是Tsiotras等[7-8]提出的一种航天器姿态参数,通过两次坐标旋转实现两个坐标系的转换。在自旋卫星中,可以分别使用参数w和参数z来描述垂直于自旋轴和绕自旋轴方向的运动[9-10],也可通过缺省z,仅用w来描述欠驱动控制[12-13]。因此,使用(w,z)参数来描述光学环扫成像卫星这类具有自旋运动特征的卫星姿态运动更加直观,且参数w的运动学相对参数z独立,有利于实现高精度控制。
新体制光学遥感卫星变转速环扫控制问题,关键在于在固定的相机关机时间段内,通过变转速环扫,保证在下一次相机开机时刻,自旋相位角和自旋角速度均达到期望值。对于在设定的终端时刻达到指定终端状态的问题,一种思路是采用最优控制的方法,通过建立代价函数,求解最优轨迹。然而,通过极大值原理求解最优控制问题的开环控制方法鲁棒性较差[4,14-15]。而有限时域的控制方法数值计算量较大,在轨应用难度较大[16]。另一种思路是采用有限时间的终端滑模控制方法。滑模控制常被用来应对系统扰动和不确定性[17-18],将其与有限时间控制理论相结合,从而实现对收敛时间的限定。有限时间控制理论由Bhat等[19]提出,在初始状态已知的情况下,可以预测收敛时间的上界。在有限时间控制理论的基础上,Polyakov等[20]发展了固定时间控制理论,其收敛时间的上界与初始状态无关。有限时间控制理论和固定时间控制理论都也已应用在航天器姿态控制中[21-25]。上述终端滑模控制理论只给出了收敛时间的上界,而不是精确的收敛时间。在此基础上,Sánchez-Torres等[26]发展了预设时间(predefined time或prescribed time)控制理论,给出了精确的收敛时间,相关理论也已在航天器姿态控制中有所应用[27-30],而对于变转速环扫控制问题,较大的角速度容易增大终端时刻的控制误差。此外,Geng等[31]提出了应用于航天器姿态机动的精确时间(exact time)稳定控制方法,是一种基于SO(3)的终端滑模控制方法,相关理论仅适用于rest-to-rest姿态机动,不能直接应用于变转速环扫控制。
根据对上述文献的研究,针对新体制光学遥感卫星变转速环扫姿态控制问题,本文将基于(w,z)参数,并采用固定时间跟踪控制方法,使卫星姿态在变转速环扫阶段,在固定时间内跟踪上期望的姿态轨迹。设计的期望姿态轨迹满足相机变转速环扫阶段结束时刻对应的终端约束条件,即相机开机时刻自旋角速度和自旋相位角均达到期望值。在变转速的初始阶段,采用bang-bang控制方法,使执行机构以最大力矩加减速,在尽量短的时间内完成对自旋相位角的补偿,为轨迹跟踪留出足够的收敛时间。
本文的后续内容安排如下:第1节介绍了光学环扫成像的原理,并针对变转速环扫控制问题进行了数学描述。第2节给出了(w,z)参数描述的航天器姿态运动学模型,并给出姿态运动学方程的误差形式,最后给出了光学环扫成像卫星的姿态动力学模型。第3节针对卫星变转速环扫控制问题,设计了基于(w,z)参数的姿态控制策略,包含bang-bang控制和固定时间滑模控制两个阶段,并给出了固定时间滑模控制律设计和稳定性证明。第4节通过数值仿真校验了控制策略的有效性。
1 光学环扫成像卫星变转速环扫控制问题描述
1.1 光学环扫成像原理
光学环扫成像卫星成像原理如图1所示。卫星以对地心定向的姿态运行在圆轨道上。光学相机倾斜安装,使相机光轴与卫星对地轴成固定夹角。卫星保持特征轴(图1中卫星本体坐标系ObXbYbZb中的Zb轴,原点位于卫星质心)对地心指向,通过整星以角速度Ω自旋,带动相机绕对地轴旋转,随着卫星在轨道上运动,相机视场会在地面形成螺旋形的环扫条带,多圈条带拼接即可实现宽幅成像。
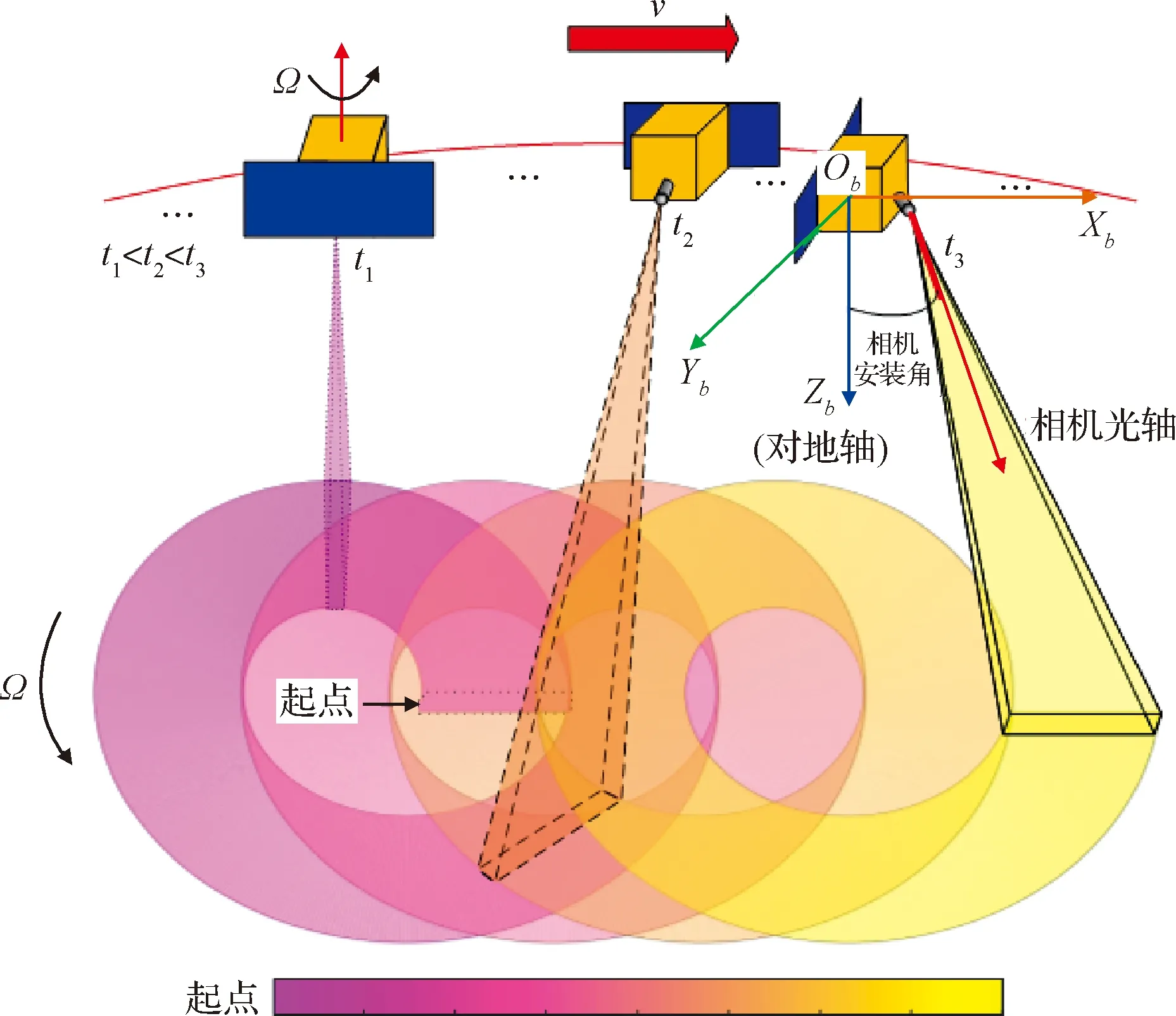
图1 光学环扫成像原理Fig.1 Principle of conical scanning imaging
从图1可以看出,不同圈次的环扫条带之间存在大量的重叠区域。为了减少重复的数据量,从而降低数据处理和数据传输系统的负担,在实际工程应用中,往往采用相机间断开机的方法。文献[4-5]分析了快旋模式和慢旋模式下,相机间断开机的拼幅效果:快旋模式下的一个环扫周期内,相机开关机各一次,且环扫条带重叠区域较少;慢旋模式下的一个环扫周期内,相机开关机各两次,且环扫条带重叠区域较多。但是由于慢旋模式相比于快旋模式的卫星自旋角速度更小,相同曝光时间内产生的像移更小,动态传函也就更高,图像质量也就更好。为了使环扫条带重叠区域较少,同时又能获得较高的图像质量,于是就有了变转速环扫模式。变转速环扫模式下,按照是否匀转速环扫,可以将一个环扫周期分解为两个阶段:
1)定转速环扫阶段:相机开机时卫星以较慢的角速度匀速环扫以获得较高的图像质量;
2)变转速环扫阶段:相机关机时卫星加速、变转速环扫,使得卫星的环扫周期等于快旋模式周期,从而能够如快旋模式那样,减少环扫条带的重叠区域,进而减轻了卫星数据处理与数据传输的压力,同时也简化了相机的开关机逻辑。
1.2 变转速环扫控制问题数学描述
变转速环扫模式的环扫条带如图2所示,由文献[4-5]可以计算得到相机开机时的自旋角速度Ω、环扫周期T、一个环扫周期内的成像时长τ1以及成像开始时刻的相位角θ0。定义相机第一次开机的时刻为t0,经过τ1时间对应的相位角为θ1。
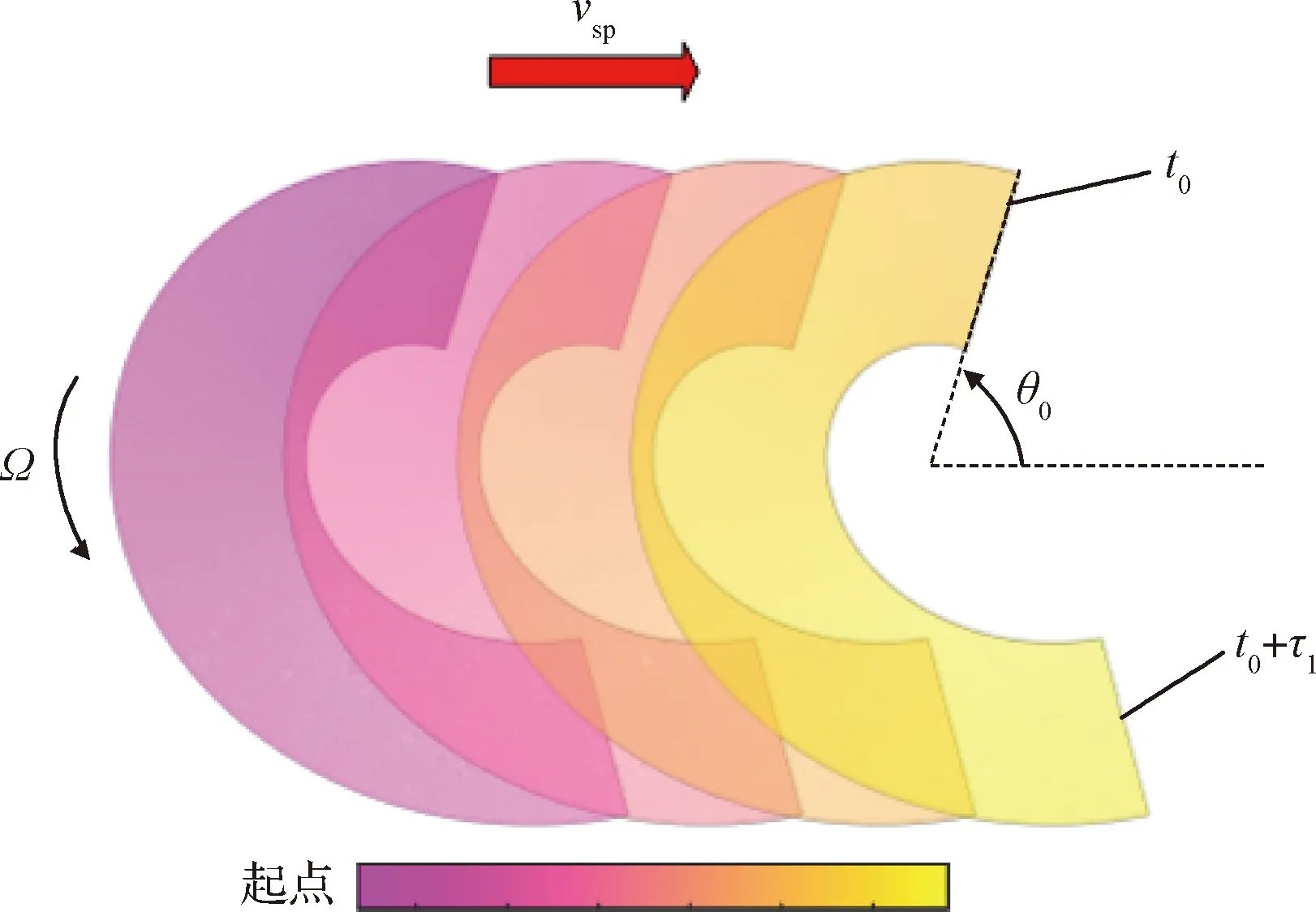
图2 变转速环扫模式的环扫条带Fig.2 Conical scanning footprint of variable-speed spin mode
于是,变转速环扫控制问题可以描述为:设计控制策略,满足下面3个条件。
1)定转速环扫阶段的角速度和相位角分别为
(1)
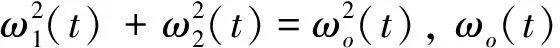
2)变转速环扫阶段的初始状态为
(2)
式中:t=t0+nT+τ1。
3)变转速环扫阶段的末状态为
(3)
式中:t=t0+(n+1)T。对于圆轨道,由于轨道角速度ωo(t)为常值,有ω1(t0+nT)=ω1(t0),ω2(t0+nT)=ω2(t0)。
本问题的主要难点在于,设计变转速环扫控制策略,使得给定系统的初始状态(2),经过τ2=T-τ1时间后,系统的状态恰好达到终端状态(3)。
2 光学环扫成像卫星姿态模型
本节将基于(w,z)参数建立光学环扫成像卫星的姿态运动学模型。同时,作为一种自旋轴指向在惯性空间中持续变化的卫星,光学环扫成像卫星通常采用整星零动量三轴稳定控制方式,通过轮控系统与卫星进行角动量交换,以便于实现灵活的姿态机动和自旋轴指向控制。因此,本文将光学环扫成像卫星视作刚体航天器,基于三轴轮控系统建立姿态动力学模型。
2.1 (w,z)参数描述的航天器姿态运动学模型
首先,参数w被定义为如下的复数:
(4)
式中:(a,b,c)表示从惯性坐标系经过一次坐标旋转后,中间坐标系的Z轴在卫星本体坐标系下单位球面上的投影坐标,从而有a2+b2+c2≡1[8]。
根据上述定义方式,卫星本体坐标系相对惯性坐标系的坐标转换矩阵为
Cbi=C(w,z)=C2(w)C1(z)
(5)
式中:C1(z)和C2(w)表征两次坐标旋转,定义如下:
(6)
(7)
(w,z)参数描述的姿态运动学方程如下[8]:
(8)
(9)

用(wr,zr)表示航天器本体相对惯性系的期望姿态,用ωr表示航天器本体相对惯性坐标系的期望角速度。在本文后续的分析与设计中,不妨取式(1)~(3)中的t0=0,于是对于光学环扫成像卫星,有
(10)
对上式求导有
(11)
定义误差w参数为
(12)
式中:ae,be和ce可以通过下式计算得到。
ae=Cbr(1, 3),be=Cbr(2, 3),ce=Cbr(3, 3)
(13)

(14)
式中:ξe=atan2(Ce1(1, 2),Ce1(1, 1)),函数atan2(y,x)表示以x和y的符号决定象限的反正切值,即
(15)
定义误差角速度为
ωe=ω-Cbrωr
(16)
于是,式(12)和(14)定义的误差(w,z)参数同样满足如下形式的运动学方程:
(17)
(18)
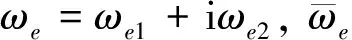
2.2 航天器姿态动力学模型
光学环扫成像卫星的姿态动力学模型为
(19)
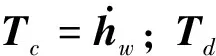
(20)
如前文所述,光学环扫成像卫星通常采用整星零动量三轴稳定控制,因此应满足如下的假设条件:
假设 1.卫星的姿态角速度ω有界,从而动力学方程中的叉乘项ω×(Jbω+hw)也有界,且接近于0。
假设 2.干扰力矩Td是有界的。
假设 3.令Jb=Jb0+ΔJb,式中:Jb0是卫星转动惯量矩阵的已知部分,ΔJb是卫星转动惯量的未知部分,且未知部分是有界的。
将误差角速度ωe的定义式(16)代入姿态动力学方程(19)可以得到
(21)
根据假设3,上式可改写为
(22)

3 变转速环扫控制方法
针对光学环扫成像卫星变转速环扫控制问题,本节将设计控制策略,并基于(w,z)运动学参数,设计相应的固定时间滑模控制律。
3.1 控制策略
变转速环扫控制策略首先要设计出期望的变转速环扫阶段的姿态轨迹,然后确保在变转速环扫阶段结束前实现对轨迹的稳定跟踪。于是将卫星的一个环扫周期按照控制律分解为两个控制阶段,分别是bang-bang控制阶段和固定时间滑模控制阶段。其中,bang-bang控制阶段从定转速环扫阶段结束时开始,即相机关机时刻开始,以最大的控制力矩使卫星加减速自旋,目的在于使卫星在最短的时间内转过最多的角度,为固定时间控制阶段留有更多的收敛时间;固定时间滑模控制阶段在bang-bang控制结束开始,目的在于使卫星在下一次相机开机前抵消bang-bang控制阶段的开环控制误差,实现稳定跟踪。
根据上述控制策略,卫星Zb轴的期望角速度轨迹如图3所示,bang-bang控制阶段经过τ3时间加速,执行机构角动量达到饱和,于是以最大角动量运转τ5时间,再减速下来,总计持续2τ3+τ5时间;固定时间滑模控制阶段需要确保系统在不超过τ4=τ2-2τ3-τ5的时间跟踪上期望轨迹。特别地,如果执行机构角动量足够大,在bang-bang控制阶段不会发生饱和,则图3中τ5的时长将退化为0。固定时间滑模控制阶段期望姿态和姿态角速度轨迹变化速度小,容易实现高精度跟踪,并且在相机开机时刻期望姿态和姿态角速度轨迹光滑无折点,不会影响跟踪精度。
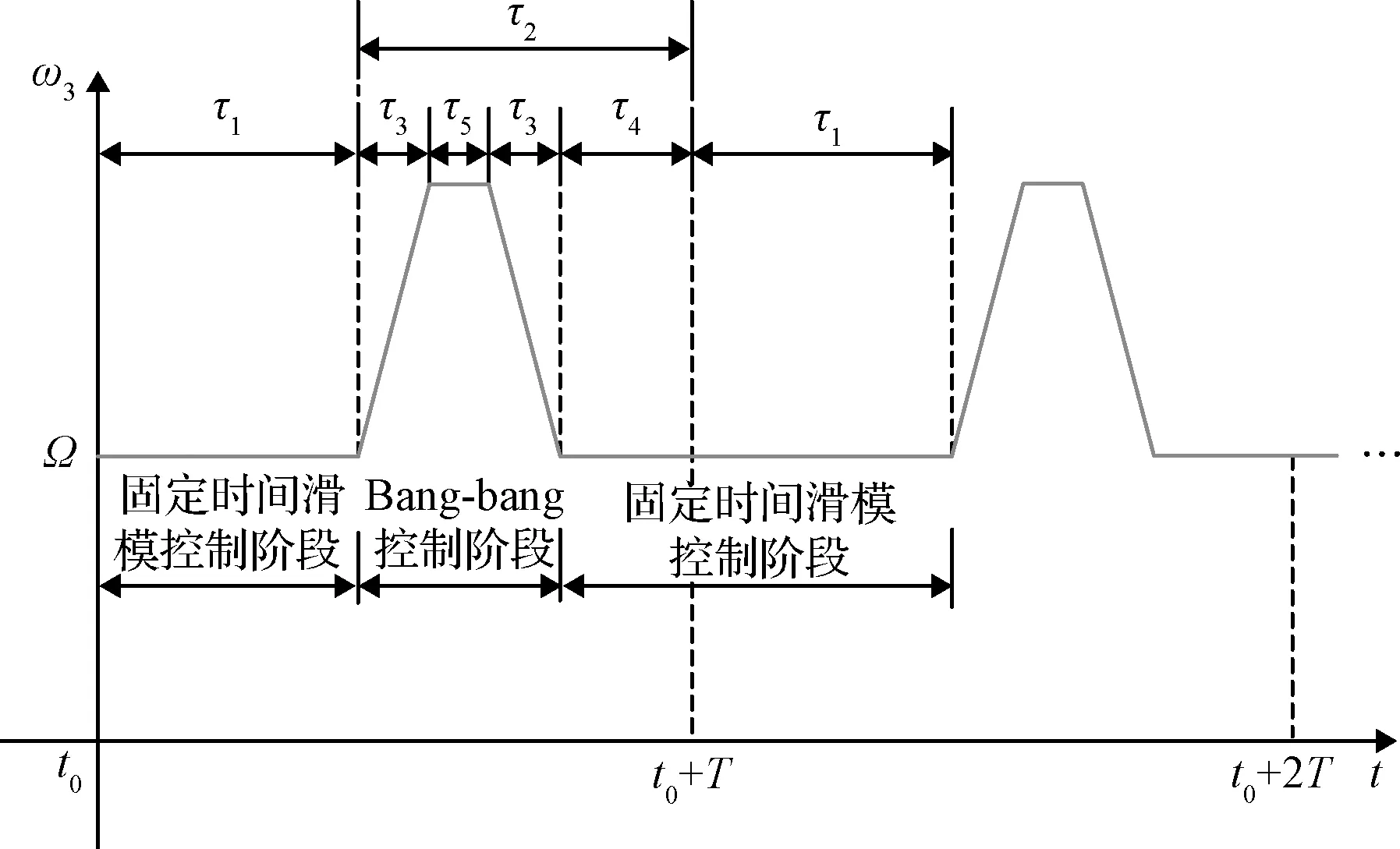
图3 卫星Zb轴的期望角速度轨迹Fig.3 Reference angular velocity track of Zb axis of satellite
接下来给出图3中τ3和τ5时长的计算方法。设执行机构能为Zb轴提供的最大控制力矩为Tm,z(方向与Zb轴的环扫角速度方向相同),执行机构能为Zb轴提供的最大角动量为hzm,Zb轴转动惯量的已知部分为Jbz0,于是最大角加速度的理论值为aω=Tm,z/Jbz0,最大角速度的理论值为ωzm=hzm/Jbz0。首先判断bang-bang控制阶段执行机构角动量是否饱和,若不饱和,则应满足如下条件:
Ω+aωτ3≤ωzm
(23)
(24)
式(24)的解为
(25)
将式(25)计算得到的τ3值代入不等式(23),如果不等式成立,则认为bang-bang控制阶段执行机构角动量不饱和,τ3直接按照式(25)取值,τ5=0;如果不等式不成立,则认为bang-bang控制阶段执行机构角动量会饱和,τ3的值取为
(26)
然后根据控制策略,可以得到下式:
ΩT+aωτ3(τ5+τ3)=2π
(27)
由上式可以解得τ5的值为
(28)
此外,由于Xb轴和Yb轴的角速度分量较小,最大不超过轨道角速度,无需单独设计控制律。因此bang-bang控制阶段Xb轴和Yb轴的控制律不妨直接沿用下面的固定时间滑模控制阶段的控制律。
3.2 变转速环扫控制器
定理 1.对于动力学模型如式(19)~(22)的光学环扫成像卫星,采用如式(29)~(31)所示的变转速环扫控制器(设初始时刻t0=0),能够实现在一个环扫周期T内,相机开机期间以角速度Ω定转速环扫,相机关机期间变转速环扫,并且在下一次相机开机时刻转到特定的相位并保持环扫转速为Ω,即给定系统的初始状态(2),经过τ2=T-τ1时间后,系统的状态恰好达到终端状态(3),并保持姿态的稳定跟踪。式(29)中,u(t)=[u1(t),u2(t),u3(t)]T,前3行用来描述bang-bang控制阶段,Zb轴以最大力矩Tm,z加减速,Xb轴和Yb轴沿用固定时间滑模控制律,第4行用来描述固定时间滑模控制阶段,三轴均使用固定时间滑模控制律。
(29)
K1sig(s)α3-(K2+Θ)sgn(s)
(30)

(31)

sgn(x)=[sgn(x1), sgn(x2), sgn(x3)]T
(32)
sig(x)v的定义如下:
sig(x)v=[sgn(x1)|x1|v,sgn(x2)|x2|v,
sgn(x3)|x3|v]T
(33)
abs(x)v的定义如下:
abs(x)v=[|x1|v,|x2|v,|x3|v]T
(34)
首先给出关于固定时间控制理论的两条引理。
引理 1[20].对于如下的非线性系统:
(35)
式中:x∈Rn,f:R+×Rn→Rn是一个非线性时变函数,并且在原点x=0附近的开放邻域U0内连续。如果该系统是李雅普诺夫稳定的,并且存在连续的径向无界函数V:Rn→R+∪{0}满足对任意的x(t),有下式成立:
D*V(x(t))≤-(αVp(x(t))+βVq(x(t)))k
(36)

(37)
如果所定义的李雅普诺夫函数的初值满足V(x(0))≤1,则收敛时间τ满足
(38)
引理 2[22].对于系统(35),如果该系统是李雅普诺夫稳定的,并且存在连续的径向无界函数V:Rn→R+∪{0}满足对任意的x(t),有下式成立
(39)
式中:α,β,η,p,q>0,并且p<1,q>1,则系统(35)在固定时间内全局收敛至原点x=0,则且系统(35)到达V(x)≡0的时间τ满足
(40)
如果所定义的李雅普诺夫函数的初值满足V(x(0))≤1,则收敛时间τ满足
(41)
下面只需证明通过设计控制参数,能够使固定时间滑模控制律(30)在不超过τ4的时间内消除bang-bang控制阶段的开环控制误差。
证.固定时间滑模控制的收敛时间可以分为两部分:到达时间和滑动时间。其中,到达时间是指系统从初始状态到达滑模面的时间,滑动时间是指系统从在滑模面上滑动到姿态稳定的时间。因此,固定时间滑模控制器收敛性证明也分为到达阶段和滑动阶段两部分来考虑[32]。
1)到达阶段
对式(31)求一阶微分,在等号两边同乘Jb0,并代入式(22)可得
(42)
定义关于滑模变量s的李雅普诺夫函数如下:
(43)
对上式求一阶微分,有
(44)
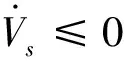
引理 3[22].对于任意的xi∈R,i=1,2,…,n,如果v>1,则
(45)
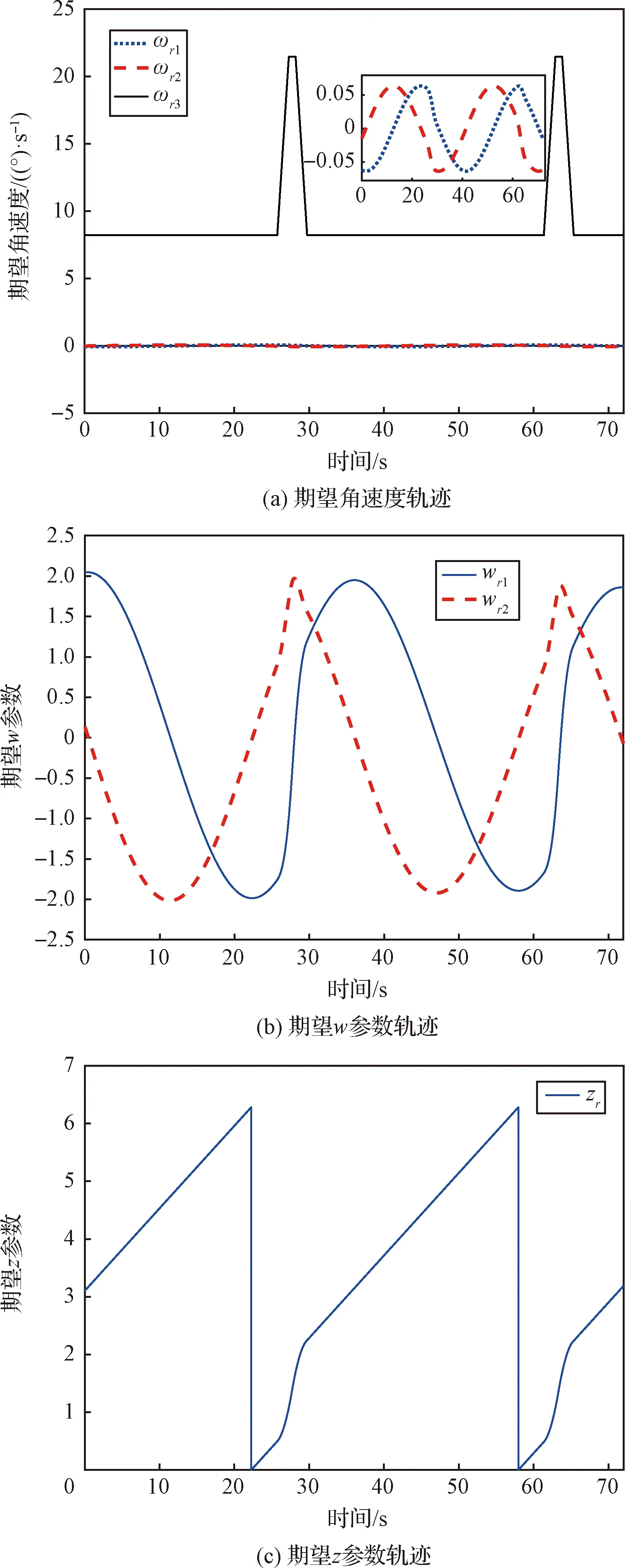
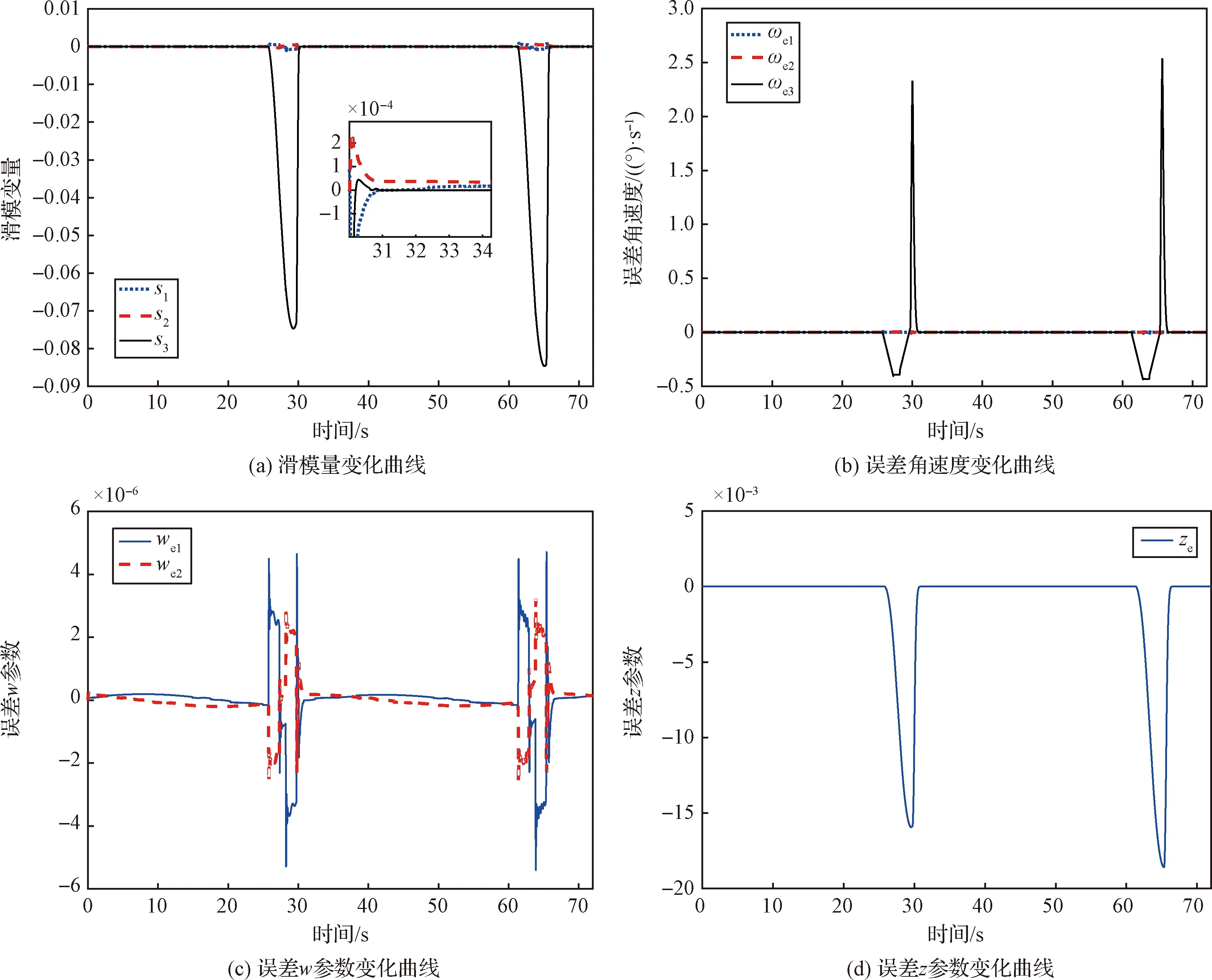
引理 4[25].对于任意的xi∈R,i=1,2,…,n,如果0 (46) 推论 1.根据引理4可以得知,对于任意的xi∈R,i=1,2,…,n,用x表示矢量[x1,x2,…,xn]T,则 (47) 根据引理3和推论1,式(44)满足 (48) 式中:ϑ=min{e|e=Θi-|di|(i=1,2,3)},λmin(·)和λmax(·)分别表示矩阵奇异值的最小值和最大值。根据引理1可知,滑模变量s是固定时间收敛的。 2)滑动阶段: 当滑模面满足s=0时,有下式成立: ωe= μ4sig(ζe)α2 (49) 针对误差参数we定义如下的李雅普诺夫函数: (50) 式中:|we|表示复数we的模。式(50)对时间求一阶微分,并将误差运动学方程(17)和式(49)代入微分方程可以得到 μ2(|we1|+|we2|)-μ2|we|2· (|we1|+|we2|) (51) 根据推论1有|we|≤|we1|+|we2|,将其代入式(51)有 (52) 根据引理2可知,误差参数we是固定时间收敛的。 注意到,当we→0时有ωe→0,于是关于ze的运动学方程(18)可以简化为 (53) 针对误差参数ze定义如下的李雅普诺夫函数: Vze=|ze| (54) 上式的右导数为 (55) 式中:sign(·)函数定义如下: (56) 将式(53)代入式(55)可以得到 D*Vze=sign(ze)ωe3=-μ3|ze|α1-μ4|ze|α2 (57) 根据引理1可知,误差参数ze是固定时间收敛的。 此外,在本问题中,bang-bang控制阶段的开环控制误差主要来源于动力学方程叉乘项、卫星转动惯量误差和干扰力矩,根据假设1~3,这些误差都是有界的,且误差值不会太大,从而可以满足下面的假设。 假设 4.从bang-bang控制阶段切换到固定时间滑模控制阶段时,式(43)、(50)和(54)所定义的李雅普诺夫函数的值均不大于1。 在假设4的条件下,根据引理1和引理2,所设计的固定时间滑模控制器总的收敛时间满足: (58) 式中:twe,tz和ts分别是we,ze和s的收敛时间。 综上所述,通过设计控制参数,使得收敛时间twz≤τ4成立,可以保证固定时间滑模控制律在不超过τ4的时间内消除bang-bang控制阶段的开环控制误差。 证毕。 (59) 式中:ε是一个小正数。 注3.为了防止在误差姿态趋近于0时,控制律中的负数指数项出现奇异或导致期望力矩过大,当误差姿态参数ze接近于0时,设置能满足姿态控制精度的姿态误差参数绝对值的下限: (60) 本节将选取文献[4]使用的光学环扫成像卫星任务模型(见表1)和像质评价标准。 表1 任务参数Table 1 Mission parameters 根据文献[4]所述的像质评价标准,为了使像质能够适用于详查任务,应使单次曝光时间内的像移不超过1个像元分辨率,从而可以得到成像期间的自旋角速度Ω应不超过8.211 (°)/s。将其代入文献[4]中的计算公式可以得到,在一个环扫周期内,相机开机时的环扫相位角θ0=73.763°,相机开机时长τ1=25.544 s。由于相机帧频为4 Hz,故对τ1向上取0.25 s的整数倍,即τ1=25.750 s,对应一个环扫周期内相机关机时长τ2=9.861 s。 卫星的结构参数和执行机构控制能力如表2所示。根据卫星工程参数可以得到角加速度的理论值aω=8.594 (°)/s2。此外,干扰力矩Td的组成包括重力梯度力矩、气动力矩和太阳光压力矩等。根据卫星轨道参数和结构参数,将式(22)中的集总不确定性d的上界取为Θi=2×10-6N·m(i=1,2,3)。 表2 卫星参数Table 2 Satellite parameters 上表中,气动力压心和太阳光压压心坐标是在卫星本体坐标系ObXbYbZb下描述的。 首先根据表2给出的执行机构最大角动量,代入式(26)可以得到τ3=1.541 s。根据式(28),bang-bang控制阶段执行机构饱和时长τ5=0.909 s。从而可以得到固定时间滑模控制阶段的收敛时间不应超过τ4=τ2-2τ3-τ5=5.869 s。根据3.1节设计的控制策略,可以得到期望角速度和期望(w,z)参数的轨迹如图4所示。从图4(a)中可以注意到,Xb和Yb轴的角速度为轨道角速度ωo的分量,因此其变化轨迹类似于以环扫周期为周期的正(余)弦函数。由于参数wr表征垂直于自旋轴的运动,因此从图4(b)可以看出,其变化轨迹也类似于以环扫周期为周期的正(余)弦函数。由于参数zr表征绕自旋轴的运动,因此在图4(c)中,其变化轨迹以环扫周期为周期在[0, 2π)范围内运动。 图4 期望角速度和期望(w,z)参数轨迹Fig.4 Reference angular velocity and (w,z) parameter’s tracks 将上述控制参数代入控制器(29),给出两个环扫周期内的姿态仿真结果如图5所示。由图5(a)可以看出,滑模量在不超过1.5 s的时间内收敛到滑模面s=0附近的邻域内;图5(b)显示了姿态角速度变化曲线,姿态角速度控制精度优于2×10-4(°)/s;由图5(c)可以注意到,由于bang-bang控制阶段产生的开环控制误差主要体现在Zb轴上,而误差w参数反映的是Xb和Yb轴的控制误差,因此在从bang-bang控制阶段切换到固定时间滑模控制阶段的时刻前后,误差w参数的量级变化不大,误差w参数的控制精度优于2×10-7,根据文献[9],在小偏差的情况下,w参数的偏差值约为偏差角弧度值的一半,因此Xb和Yb轴的姿态控制精度(亦即自旋轴的指向精度)约为4×10-7rad(即2.292×10-5(°));误差参数z的值即为自旋相位角偏差的弧度值,如图5(d)所示,Zb轴的姿态控制精度优于2×10-8rad(即1.146×10-6(°))。根据图5(b)~(d),误差角速度和误差姿态的实际收敛时间均不超过1.5 s,实现了在不超过τ4的时间内收敛。 图5 姿态仿真结果Fig.5 Attitude simulation results 从仿真结果可以看出,基于(w,z)参数的控制策略将卫星的对地轴定向和自旋运动分开描述,使得垂直于自旋轴和绕自旋轴的运动在控制过程中的相互影响较小,在抖振抑制较好的情况下,能够实现较高的控制精度。 为了实现新体制光学遥感卫星变转速环扫的闭环控制,本文给出了变转速环扫控制问题的数学模型,基于(w,z)参数设计了bang-bang控制与固定时间滑模控制相结合的控制策略,给出了期望的姿态轨迹,并且证明了设计的控制策略能够在下一周期相机开机时达到期望的自旋角速度和自旋相位角。仿真结果表明,所提出的控制策略能够有效地实现光学环扫成像卫星变转速环扫控制。在抖振抑制效果较好的情况下,基于(w,z)参数的控制方法能够实现较高的控制精度。本文所提出的控制策略对于光学环扫成像卫星变转速环扫控制具有工程指导价值。在本文所提出的控制策略的基础上,也可结合星载计算机算力、姿态确定误差等其它工程技术指标,对控制策略和控制律进行适应性改进。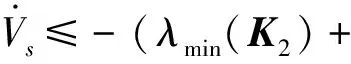


4 仿真校验
4.1 仿真条件


4.2 基于(w,z)参数的控制策略仿真分析

5 结 论
