基于多波束技术的内陆水下地形三维测绘方法

温 旋，孔德博，杜丽雯

(江苏省工程勘测研究院有限责任公司，江苏 扬州 225002)

我国领土面积较大，多山多水且东西向横跨地形复杂[1-2]，使河流落差较高，为我国建设水电站提供了优良的条件。同时我国海岸线长达1.8万km，海底油气储存量巨大，非常利于海洋勘探。但在进行海洋油气勘探和构建水电站时，受河道和海底复杂环境影响，水利工程建设难度较大。

目前研究水利工程地形测绘方法很多，如张建芳[3]设计的船载激光地形测绘方法，该方法使用激光扫描仪获取海岸地形范围，以海岸边缘信息为基础，使用摄像机拍摄海底图像，经过坐标系转换和点云数据配准后，获取海底等高线实现海底地形测绘，但该方法使用摄像机拍摄的海底图像存在大量噪声干扰，且该方法并未对图像噪声进行预处理，导致其获取的海底地形等高线存在误差，精度不足。仲照东[4]则设计了三维地形测量系统，该系统通过建立GIS地理信息数据库，使用无人机搭载激光雷达方式获取水底地形信息，经过数据融合后实现水底地形测绘信息。但该系统仅适用于Linux操作系统，不具备兼容性，导致其适用范围较小。

为了解决上述文献成果的不足，提高测绘误差和适用性，本文提出了基于多波束技术的水利工程地形三维测绘方法。多波束测量技术是通过透镜、反射等途径形成的多个元波束，利用该波束包围的区域获取测绘目标的技术，该技术被应用于地形测绘、水底基质分析及建筑工程定点等，具备较高的精度。三维技术则是通过对测绘目标进行多方位数据提取，确定其三维坐标的技术，该技术通过构建目标模型，为用户呈现可视化的测绘目标[5]，为水利工程建设提供立体的数据基础。

本文将多波束技术和三维技术相结合，设计基于多波束技术的水利工程地形三维测绘方法，实验结果表明：本文方法不仅将测绘误差降低到1.18m，还使测绘目标要素三维符号化，可以在任何操作系统上完成测绘目标三维建模过程，具备兼容性，同时测量的水下地形距离不受环境温度、水密度及其他参量影响，适用性较强。为水利工程建设提供可视化的数据基础。

1 水利工程地形三维测绘

1.1 多波束声呐成像模型构建

1.1.1激励信号函数

多波束声呐成像为视声呐成像技术的一种，其通过多波束声呐仪发射多波束声波，声波在水体内扩散时，遇到障碍物会形成散射波[6]，散射波自其来向返回至多波束声呐仪接收器内，形成若干目标声呐回波。通过向测绘目标区域发射数个多波束声波，依据其若干目标回波信号形成测绘目标图像[7]。在向测绘目标区域发射声波时，需设置其激励信号函数，以提升多波束成像声呐仪的成像质量。

多波束声呐成像仪发射的声波包括单频矩形脉冲信号和线性调频脉冲信号[8]，设置单频矩形脉冲信号和线性调频脉冲信号的数学函数表达式分别为：

(1)

(2)

式中，e—自然常数；f0—单频矩形脉冲信号中心频率；Q—脉冲宽度；ω—参考点输出波形；t—脉冲周期；k=F/t为脉冲信号变化率，F—声波调频宽度。

利用公式(1)和(2)约束单频矩形脉冲信号和线性调频脉冲信号的频率与宽度，其回波信号更为均匀与稳定，生成的测绘目标图像更为精准。

1.1.2水底数学模型

在上节生成的测绘目标图像基础上测绘水底目标时，将水底目标看作刚性球体，声呐基阵参考阵元由(x1，y1，z1)表示，则测绘目标的数学表达式如下：

(x-x0)2+(y-y0)2+(z-z0)2=L2

(3)

式中，L—探测距离；(x，y，z)—多波束声呐基阵内参考点；(x0，y0，z0)—测绘目标三维坐标原点。

设φ、θ分别为回波相位差和波束角，则探测目标坐标值(x′，y′，z′)的表达式为：

(4)

多波束声呐基阵内参考点与测绘目标上任意点直线表达式为：

(5)

结合公式(4)和(5)得到联合测绘目标和直线方程的参数，表达式为：

(6)

利用公式(6)获取声波辐射测绘目标区域，公式(5)内z值为0，可获取到测绘目标的阴影覆盖区域。

1.1.3回波信号模型

水底测绘目标阻挡声波形成反向声呐回波后，由于声波过长或者测绘目标较大[9-10]，导致声呐图像分辨率不够清晰，为此依据声呐图像分辨率将其划分为若干较小单元，依据较小单元内的声呐散射点描述声波受测绘目标阻挡后的回波强度(如图1所示)。

图1 多波束声呐回波方程示意图

由图1可知，在声呐传播时，SL为辐射声源级，TL为水面下方的声级，由于传输介质不同，产生能量损失[11]，RL为水面上方的损失声级，Ts为反射点。结合声波、测绘目标和多波束声呐发射仪参数等，对当前多波束声呐仪接收声呐回波状态进行预判。回波信号损失后返回到基阵时的表达式如下：

RL=SL-2TL+TS

(7)

式中，TS—测绘目标强度。

利用声呐方程获取到测绘目标的声压数，令σ为反射系数，PS为信号功率，测绘目标的反射回波声压表达式如下：

(8)

式中，P—测绘目标的声压；k—扩展参数；α—介质吸收系数；w—校正系数；r—信号辐射区域跨度；P(θ)—指向性函数；d—阵元间隔；F—线阵列；λ—波长；θ—多波束声呐发射仪的预判角度，sinθ—预判角度正弦值。

经过上述过程，获取到测绘目标的反射回波声压，生成射频信号，作为回波信号，其中存在大量干扰噪声，需对回波信号进行聚集和滤波匹配处理。

1.2 回波信号处理

对多波束成像声呐模型获取到的测绘目标回波信号进行聚集和滤波匹配处理，使测绘目标声呐图像特征更为清晰。

令l=1，2，…，N，为基阵线阵列阵元，该阵元接收到的测绘目标区域分辨单元为(m，n)，则该分辨单元的子单元的回波信号输出表达式如下：

(9)

式中，A(m，n，l)—子单元的回波信号；K—分辨单元内子单元数量；L(m，n)s—测绘目标区域高分辨单元s的子阵元回波函数；P(m，n，i)—阵元接收到的回波信号；r2(m，n)—测绘目标区域分辨单元的滤波匹配函数。

基阵所有单元接收到的回波信号聚集为多波束测深信号[12]，其中，进行离散傅里叶变换后，通过相移方法获取第q个波束，q=1，2，…，Q，第q个波束的含噪回波信号表达式为：

(10)

在回波信号相位噪声内引入模数转换器，分析离散梯度，进行聚集处理，输出积累后的回波信号为：

(11)

受回波信号内相位噪声影响，对聚集处理后的回波信号进行滤波匹配处理。

将回波信号输入至匹配滤波器内，利用该匹配滤波器输出的回波信号即为经过压缩处理的回波信号。令T为存在干扰噪声的复杂信号，其线阵列数值≥1，此时该回波信号长度可由T0=1/B=T/N表示，回波信号的功率由P0表示，则信号功率P和长度T与输出信号功率P0和长度T0关系如下：

P0×T0=P×T

(12)

通过上述公式可知，输出信号功率P0约等于NP，复杂的回波信号经过匹配滤波处理后，信号长度得到缩减，而信号功率则得到提升，由此实现多波束声呐呈现的距离分辨率提高，得到增强后的测绘结果。

1.3 测绘目标云数据提取

经过1.1小节和1.2小节获取到测绘目标图像后，以测绘目标声呐图像内的像素点作为点云数据，并将该图像内的测绘目标轮廓像素点换算成三维空间坐标。

由于测绘目标的声呐图像为水体成像，在提取测绘目标时，仅能提取其二维坐标[13]，此时利用新坐标参数ζ将测绘目标的二维转换为三维，该转换过程称为点云数据拼接，其步骤如下：

在点云空间三维坐标系内，横轴与垂直轴均对应任意单一测绘目标声呐图像，垂直坐标为垂直方向，纵坐标为法向量方向，则纵坐标方向为多波束声呐发射方向。此时多波束声呐发射方向表达公式如下：

y=(t×v)ζ

(14)

式中，y—多波束声呐发射方向的纵坐标轴；v—声呐移动速度；t—多波束声呐获取测绘目标图像间隔时间。

利用公式(14)可将测绘目标的二维信息转换为三维信息，完成测绘目标点云数据提取。

1.4 散乱点云数据平滑处理

测绘目标点云数据提取完成后，测绘目标边缘的点云数据点存在散乱情况[14-15]，影响测绘结果精度，需对测绘目标边缘的散乱点云数据进行平滑处理，其步骤如下。

1.4.1特征区域判定

令W为散乱点云数据内的测绘点，n(W)为该测绘点的单位法矢。Nbs(W)为测绘点的邻域中点集合，该集合内第i个元素Wi与测绘点W的法矢夹角由αi表示，该法矢夹角的变化率表达公式如下：

(15)

式中，αj—元素的法矢夹角。

通过设定法矢夹角阈值，对比v与阈值大小，当v小于该阈值时，则判断点位于特征区域内。

1.4.2测绘点法矢量修正

计算测绘点法矢夹角变化率vi后，其中i=1，2，…，k，计算公式如下：

(16)

式中，n(W)—测绘点顶点修正函数；nk(W)—测绘点法矢夹角计算函数。

1.4.3调整测绘点位置

利用公式(16)结果对测绘点位置进行调整，其表达公式如下：

Wnow=Woriginal+∑ψE(T)/∑ψ

(17)

式中，Woriginal—未调整前测绘点位置；T—三角片；Wnow—测绘点位置调整函数；ψ—三角片面积；E(T)—测绘点投影。经过上述步骤可实现散乱点云数据平滑处理。

1.5 水底地形三维建模

将经过平衡处理后的点云数据输入至3DMAX软件内，建立测绘目标三维模型并将其保存为.3ds格式文件，使用ArcScene三维软件即可调取该.3ds格式文件创建点云测绘目标三维模型，经过连接点、线使测绘目标要素三维符号化，可以在任何操作系统上完成测绘目标三维建模过程，具备兼容性。利用该模型实现水利工程地形三维测绘。

2 实验分析

以某省适合构建水电站河流水域为实验对象，使用MATLAB仿真软件模拟水域环境，使用本文方法对其水下地形展开测绘。

2.1 测绘目标距离测试

以多波束回波信号的延时和距离数值为基础，对多波束回波信号的距离和延时关系进行拟合，测试本文方法的测绘水下地形距离能力，结果如图2所示。

图2 水底地形距离测绘结果拟合曲线

分析图2可知，初始回波信号数据点的距离随着其延时时间的增加而增加。初始数据分布为散点状态，经过本文方法处理后，拟合曲线呈现平滑状态，该结果表明本文方法测量的水下地形距离精度高的同时，不受环境温度、水密度以及其他参量影响，对水底地形距离测绘结果较为精准，且环境适用性较强。

2.2 多波束点位误差测试

使用多波束测绘水下地形时，需对水下地形定点，在MATLAB仿真软件内设置10个水下地形定点位置，编号为1～10，使用本文方法对其点位进行测绘，结果见表1。

表1 多波束点位误差 单位：m

分析表1可知，使用本文方法对水下点位测绘时，测绘坐标与已知点位坐标相差不大，其中最大偏差出现在第2个定点位置的横轴方向，但偏差仅为1.18m，测绘误差百分比约为0.099%，该数值表明本文方法测绘水下地形误差较低，可有效作为水利工程建设技术含量较高的水下地形数据。

2.3 散乱点云平滑处理

散乱点云平滑处理是提高测绘数据质量的一种有效手段。以一组该水域水下地形声呐图像为实验对象，测试经过本文方法对其散乱点云平滑处理后，声呐图像呈现效果，结果如图3所示。

图3 声呐图像平滑处理前(左)与处理后(右)的结果对比

由图3可知，未经过平滑处理的声呐图像整体较为模糊，水下地形边缘线不够清晰，而经过本文方法对该声呐图像进行平滑处理后，该声呐图像的清晰度得到一定程度提升，且水下地形的边缘轮廓点均已被标出。经过平滑处理后的水下地形声呐图像更能呈现其自身特征。上述结果表明：本文方法处理水下声呐图像平滑效果较好，也从侧面说明其水下地形测绘能力好。

2.4 水下地形三维模拟效果

使用本文方法模拟该水域某区域水下地形，模拟结果如图4所示，可有效模拟水下地形，且依据颜色标准可分析出该水域水下地形起伏状况，为水利工程建设提供良好的参考条件。

图4 水下地形三维模拟

为更清晰呈现本文方法测绘的水下地形效果，依据图4的水下地形三维模型，绘制该水域水下地形剖面图(如图5所示)。

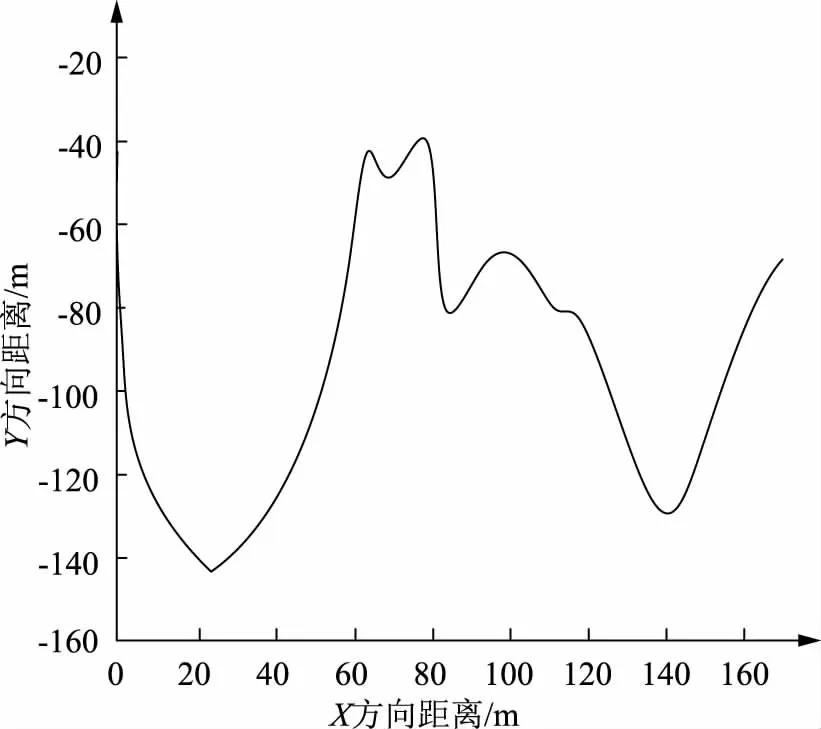
图5 水下地形剖面图

分析图5可知，该水域水下地形在X轴方向表现为深谷-峰-谷的形态，深度数值最大出现在X轴方向约为23m处，谷深度约为-140m。自X轴方向延伸，在X轴方向得58～120m位置表现为峰状，而后又呈现谷状。通过对比图4内等高颜色分布情况，水下地形剖面图与三维模拟图表现的水下地形情况较为相符。该结果表明：本文方法不仅可以有效模拟水下地形，还可呈现水下地形起伏情况，具备较好的应用性。

从工期角度测试本文方法应用效果，以水利工程一个桥墩施工工期为例，测试预计工期和使用本文方法对水下地形测绘后的施工工期变化情况(如图6所示)。

图6 施工工期

分析图6可知，该水利工程在钢围堰建设阶段、抽水阶段以及注浆阶段总工期为28d，而应用本文方法后，该水利工程桥墩建设工期仅为18d，有效缩短工期天数为10d。该结果表明：本文方法应用后，缩短水利工程建设工期效果较好。

3 结论

本文将多波束技术和三维建模技术相结合，设计基于多波束技术的水利工程地形三维测绘方法。该方法环境适用性较强，能够为水利工程建设提供重要的数据，且稳定性良好。可以有效地平滑掉噪声，提供清晰的水下声呐图像，提高水下地形测绘水平。准确且完整地呈现水下地形起伏情况，测绘水下地形，能够有效减少工期天数，大大提高了水利工程建设的效率。但由于多波束声呐工作原理的局限性，测量范围受到一定的限制。在水深较大的情况下，可能无法获取到足够的数据。在后续研究中，可以尝试新型多波束声呐技术，如宽带多波束声呐等，以拓展测量范围和提高测量精度。