机器主动学习技术在船舶和海工结构非线性水动力响应长期预报中的应用研究
2023-09-22李林斌李洛东刘日明
李林斌,李洛东,刘日明
(中国船级社,北京 100007)
0 引 言
准确预报船舶及海工结构在水动力作用下的长期极值响应是结构设计的基础,如船舶25年重现期的波浪弯矩或半潜式平台100 年重现期的气隙等。长期响应预报需要考虑两个因素,一是结构在稳定海况条件下响应的短期分布,二是海况条件的长期分布,进而将每个海况条件对结构长期极值响应的贡献率统计在内。对于非线性响应的情况(如波浪砰击颤振诱导的船舶垂向弯矩),需要针对每个海况条件,采用非线性时域模拟和统计分析方法,来获得结构的响应分布,因此非常耗费计算资源,不便于结构的设计优化和敏感性分析。
采用合理的替代方法,避免在整个海况域内进行非线性响应分析,是船舶和海洋工程领域持续研究的课题。其中,环境包络线法在海洋工程领域有较为普遍的应用[1],这是一种基于短期极值来推算长期极值的方法,即在特定重现期环境包络线设计点海况的短期最大响应基础上,乘以一系数(一般为1.1~1.3),或取短期最大响应分布的更高分位值(一般为75%至90%分位),作为相同重现期的长期极值响应,但该系数或分位值取决于结构响应的短期变异程度以及海况条件的长期变异程度,需要预先研究确定;另外一种方法是根据各海况对线性响应长期极值的贡献度,筛选出一定数量的海况,再针对这些特定海况进行更为复杂的非线性数值模拟和统计分析[2],该方法成立的前提是海况的非线性和线性响应贡献度排序大致相当,但这种假设并非普遍成立,同时并非所有的结构线性响应都存在且容易获得。近年来,采用机器学习技术的回归算法得到越来越多的重视和应用,该方法一般采用平均取样[3]或拉丁超立方体抽样技术[4],选取一定数量的海况进行水动力分析,获得结构响应的分布参数,用以训练代理模型,并基于代理模型来预测其他海况对应的响应分布参数。由于需要保证代理模型在整个输入域内预测结果的准确度,训练集样本数往往很大,导致非线性响应分析的计算量依然巨大。总之,这些替代性方法的应用都存在一定的局限性。
本文提出一种新方法进行非线性水动力响应的长期预报。该方法采用机器主动学习技术,通过机器学习模块和水动力计算模块的交互,以循环迭代的方式,贯序筛选对极值响应贡献最大的海况进行非线性时域分析,并将分析结果追加到训练集中,持续训练机器学习模型,进而实现预测值向真实值的快速收敛。
在后续的章节中,作者将简要介绍采用传统方法进行非线性水动力响应长期预报的过程;阐述如何利用高斯过程回归(GPR,Gaussian Process Regression)和贯序取样(Sequential Sampling)技术来建立机器主动学习模型;并以两型大型集装箱船为算例,采用机器学习模型对弹性体砰击颤振弯矩和刚体非线性波浪弯矩进行预测;通过与真实值的比较,验证模型的高效性和准确性,展示其在工程上的应用价值;最后给出几点研究结论和建议。
1 非线性水动力响应的长期预报
1.1 长期极值响应分析
船舶和海工结构在水动力作用下的长期极值响应,无论是线性的还是非线性的,都需要考虑结构在稳定海况条件下的响应短期分布,以及海况条件的长期分布,即
式中:Q(y)为响应Y的长期超越概率,目标超越概率取决于重现期的要求;f(x)为海况x的长期分布,如波高-周期(Hs-Tz)联合概率分布函数或波浪散布图;g(y|x)为响应Y在海况x下的短期分布(超越概率)。其中,响应的短期分布g(y|x)是整个过程的核心。对于线性响应,问题相对简单,可以通过传递函数和谱分析的方法得到;对于非线性响应,就需要针对每个海况,通过非线性时域水动力计算和统计分析获得,需要在整个海况域内求解,因此是一个非常耗时的过程。下面以船舶波浪砰击颤振为例进一步说明。
1.2 船舶砰击颤振弯矩的长期预报
大型船舶,特别是大型集装箱船,由于首尾部船体大幅外飘,当以较高航速在中高海况航行时,大幅的船波相对运动会使船体受到波浪的强烈冲击,船体结构由于砰击载荷作用而发生瞬时高频振动,产生所谓的“颤振”现象,具有强非线性特征,对总体波浪弯矩影响显著,需要在船体梁极限强度分析时充分考虑。根据中国船级社《船体结构波激振动和砰击颤振直接计算评估指南》,应采用时域水弹计算和统计分析方法进行预报,包括弹性体砰击颤振诱导弯矩和刚体非线性波浪诱导弯矩。
对无限航区船舶,一般采用IACS REC No.34 推荐的北大西洋海浪散布图[5],其海况数为197 个(即:197个非零Hs-Tz参数对)。浪向角Hd的选取原则是在0°至360°之间,取间隔不大于30°,各浪向角的发生概率相等。考虑到对称性的因素,浪向角合计为7 个,如图1 所示。这样在考虑浪向后的海况总数为1379个,对如此多的海况进行逐一的非线性时域分析,对计算资源的耗费是可想而知的。

图1 浪向角Hd及编号(括号内的数字为Hd编号)Fig.1 Wave heading Hd and its numbering(the digit in brackets is the Hd numbering)
在短期海况xji(第j海况第i浪向角)条件下进行非线性时域计算,对得到的垂向波浪弯矩峰值y进行Weibull分布拟合,其超越概率为
式中,βji为形状参数,ηji为尺度参数。
垂向波浪弯矩长期极值超越概率为
式中,pj为第j海况的长期概率,pi为第i浪向的长期概率。Q( )y= 10-8所对应的响应值yex为目标极值响应,即25年重现期的垂向波浪弯矩,本文中即为弹性体的砰击颤振弯矩或刚体的非线性波浪弯矩。
海况xji对长期极值响应的贡献度Cji是一个很重要的概念,在后续的分析中会反复用到,其定义为
图2 显示了分析的总体过程。对Cji的进一步分析,不难发现长期极值响应来自于极少数海况的贡献。以13 500 TEU颤振中垂弯矩为例(具体见3.1节),贡献度前30的海况,其累计贡献度为98.3%,而这些海况仅占海况总数(1379)的0.008%,均为有义波高Hs超过12.5 m 的高海况,浪向都是迎浪或艏斜浪(1号和2号浪向角),总体情况如图3所示。

图2 时域非线性波浪载荷计算和统计分析流程Fig.2 Time domain nonlinear wave load calculation and statistical analysis process
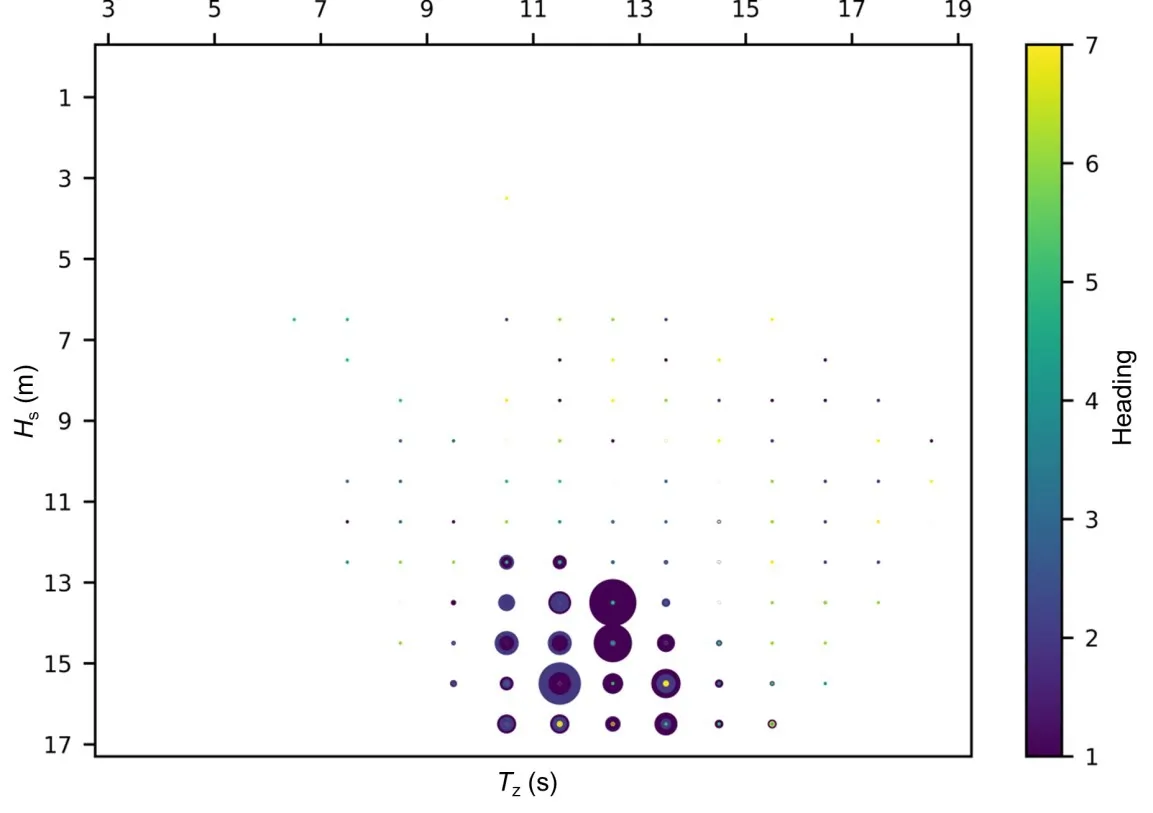
图3 海况对长期极值响应的贡献度(图中圆的直径与贡献度成正比,颜色对应浪向角)Fig.3 Contributions of sea states to the long-term extreme response(the diameter of the circles is proportional to the contributions,and the colors correspond to the wave headings)
如果能够建立一种模型,以智能和贯序方式识别出这些海况,并传递给水动力分析模块进行非线性时域分析,而不是分析全部海况,将大大减少计算资源的耗费,提高结构设计和分析效率,这正是本文研究的目的和出发点。
2 机器主动学习模型
2.1 高斯过程回归
高斯过程回归(GPR)是近年发展起来的一种机器学习回归方法[6],有着严格的统计学习理论基础,对处理高维数、小样本、非线性等复杂的问题具有很好的适应性,且泛化能力强,有着广泛的工程应用[3,7]。GPR从函数空间角度出发,定义一个高斯过程来描述函数分布,直接在函数空间进行贝叶斯推理。GPR 是任意有限个随机变量均具有联合高斯分布的集合,其性质完全由均值函数和协方差函数确定,即f(x)~GP(μ(x),k(x,x') ),其中
式中,x,x'∈Rd为任意随机变量。通常会对数据作预处理,使其均值函数等于0。假设观测过程受到加性噪声的污染,则观测值y可用如下模型描述:
式中,x为输入向量,f为函数值,ε为加性噪声污染。假设ε符合均值为0、方差为c2的正态分布,即ε~N(0,c2),则观测值y的先验分布为
观测值y和预测值f*的联合先验分布为
式中:K(X,X)=Kn=(kij)为n×n阶协方差矩阵,kij=k(xi,xj),为xi与xj的协方差;K(X,x*)=K(x*,X)T为测试点x*与训练集的输入X之间的n× 1 阶协方差矩阵;k()x*,x*为测试点x*的方差;In为n维单位矩阵。
由此可以得到预测值f*的后验分布为
为了训练GPR模型,需要设定一个协方差函数,文中我们采用了高斯径向基核函数[3]:
式中,δ2为核函数的方差参数,h为尺度参数。δ和h这两个超参数以及c需要通过机器学习(即训练)获得。
2.2 贯续取样算法
GPR 是监督学习的一种,是根据经验数据(训练集)来学习输入-输出之间的映射关系,使得给定新的输入便可得到相应的输出值(预测值)。通常情况下,训练集需要人为预先指定。相比人工神经网络、随机森林、支持向量机等其他机器学习方法,高斯过程回归的独到之处在于其预测值是一个高斯随机变量,不但可以给出预测值的最佳估计(均值),而且可以给出变异程度(方差)。
正是GPR以上独有的特点,为实现机器主动学习提供了可能,并应用于非线性动力系统的长期极值响应预报[8],即贯序找出对长期响应影响最大的输入值,将其加入到训练集,迭代更新GPR 模型,使其预测值在对长期响应贡献度最大的输入区域内变得更为准确,进而实现预测值向真实值的快速收敛。结合本文的研究目的,我们设计了一种算法,通过Python编程,开发了机器主动学习模块,并通过与水动力分析模块的交互,实现了对船舶结构非线性水动力响应的长期预报,具体步骤如下:
(1)指定初始训练集的输入集,即海况x=()Hs,Tz,Hd,进行非线性时域水动力计算和统计分析,得到训练集的输出集,即Weibull分布的形状参数β和位置参数η;
(2)对GPR模型进行训练,分别获得超参数δβ、hβ和cβ以及δη、hη和cη;
(3)利用GPR模型预测其他海况xji对应的观测值均值和,以及方差和;
Murphy指出,个体在实际展开工作活动的过程中,为了达到工作绩效目标所表现出的一系列行为,即为绩效;我国在积极展开工作绩效研究的过程中,指出了学习过程、创新行为、公民气候、技术核心即学习绩效、创新绩效、关系绩效和任务绩效四个工作绩效结构[2]。
(5)计算每一个海况的“收获函数”Aji=,找出Aji最大时对应的海况xn;
(6)将xn传递给水动力分析模块,进行非线性时域计算和统计分析,获得Weibull 分布的形状参数βn和位置参数ηn;
(7)将xn,βn和ηn追加到训练集中,重复(2)~(6),直到长期响应值收敛。
以上过程中,“下一个最优”海况的选择应考虑和平衡两个因素,一是需要距离训练集足够远(也即预测值方差足够大),二是对长期极值响应y^ex的贡献度足够大,而“收获函数”实现了这一平衡。
3 算例研究
3.1 误差分析
本文以13 500 TEU 和20 000 TEU 两型大型集装箱船为算例进行研究,建立水动力模型并进行时域水弹计算和统计分析,包括弹性体砰击颤振弯矩和刚体非线性波浪弯矩。这两型集装箱船的主要参数如表1所列。

表1 船舶主要参数Tab.1 Main parameters of the ships
首先采用传统方法,按照1.2 节所述流程,完成了全部1379 个海况的水动力计算和统计分析,并获得了长期极值响应yex,并将其作为“真实值”。
然后采用第2 章所述的机器学习模型进行长期极值响应预报。选择波浪散布图中最小和最大Hs,及其对应Tz出现概率最大的海况,对这些海况进行水动力计算和统计分析,获得对应的分布参数,作为初始训练集。
式(13)为13 500 TEU船型颤振中垂弯矩GPR模型的初始训练集:
我们采用机器学习模型迭代100次,每次迭代都获得一次长期极值响应的预报值y^ex;同时模型将根据“收获函数”,自动和贯序识别出“下一个”最重要的海况,传递给水动力模块进行时域分析。给出的误差e如式(14)所示,以反映机器学习模型的准确性:
误差分析的结果如图4~7 所示。不难看出,机器学习模型的预测结果误差随着迭代次数的增加而快速降低和收敛。虽然由于结构响应的非线性、统计过程的不确定性,以及机器学习过程的随机性等因素导致不同船型的收敛效率会有所差别,但从本文的算例看,模型迭代大约30~40 次后,其误差均可以控制在1.5%以内。加上初始训练集的14个海况,需要进行非线性水动力分析的海况总数不超过60个,相比传统方法需要分析的全部1379个海况,计算效率提高了20多倍。

图4 13 500 TEU弹性体砰击颤振弯矩误差Fig.4 Errors of the 13 500 TEU elastic hull whipping bending moments

图5 13 500 TEU刚体非线性波浪弯矩误差Fig.5 Errors of the 13 500 TEU rigid body nonlinear wave bending moments

图6 20 000 TEU弹性体砰击颤振弯矩误差Fig.6 Errors of the 20 000 TEU elastic hull whipping bending moments

图7 20 000 TEU刚体非线性波浪弯矩误差Fig.7 Errors of the 20 000 TEU rigid body nonlinear wave bending moments
图8 显示了机器学习模型贯序取样得到的前20 个海况的排序(13 500 TEU 弹性体颤振中拱弯矩)。与图3 对比可以看出,机器学习模型很好地识别出了对长期极值响应贡献度最大的海况区域,显示出机器学习技术的强大功能。
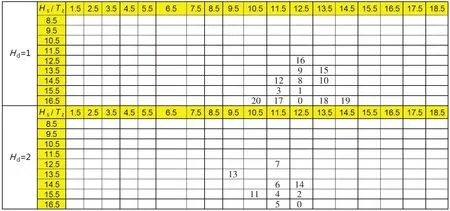
图8 贯序取样前20个海况的分布,0表示初始训练集(13 500 TEU颤振中拱弯矩)Fig.8 Scatter of the top 20 sea states by sequential sampling and 0 means the initial training dataset(the 13 500 TEU whipping hogging moment)
3.2 敏感性分析
第2章所述的机器学习模型中,初始训练集的输入集(海况)需要人为预先设定,并对收敛效率产生影响。海况涉及到三个参数,即:有义波高Hs、跨零周期Tz和浪向角Hd。我们以13 500 TEU 颤振中垂弯矩为例,通过分别改变式(13)中的这三个海况参数,进行敏感性分析,结果汇总如图9所示。

图9 训练集的敏感性分析(13 500 TEU弹性体颤振中垂弯矩)Fig.9 Sensitivity analysis of training data(the 13 500 TEU elastic hull whipping sagging moments)
(1)改变有义波高
一般情况下,船舶结构的水动力长期极值响应主要来自于大波高海况(如Hs超过10 m 的海况),图3 也清晰反映了这一趋势。因此,在确定初始训练集的下限海况时,似乎应选择更高的海况,以便提高收敛效率和计算精度,但事实并非如此。如我们选择(Hs,Tz)=(9.5,10.5)作为下限海况,上限海况保持不变,可以看到模型的收敛效率明显下降,原因在于GPR 是一种适于内插预测的机器学习方法,而外推预测时误差往往会很大,即模型对Hs低于9.5 m海况的贡献度预测产生很大误差,进而导致收敛效率降低。
(2)改变波浪周期
选择波浪散布图中的最小波高和最小周期(Hs,Tz)=(0.5,3.5),以及最大波高和最大周期(Hs,Tz)=(16.5,15.5),作为初始训练集海况,其收敛效率会有所下降,但不是很明显。
(3)改变浪向角
只保留1/4/7三个浪向,将式(13)的海况训练集样本数缩减至6个。可以看出,误差收敛效率有所降低,需要迭代更多次才能达到预期的误差范围。
根据以上分析,在确定初始训练集海况时,我们应选择波浪散布图中最小和最大Hs及其对应Tz出现概率最大的海况,以及所有的浪向角,以保证迭代效率和预测精度。
4 结 语
船舶和海工结构在水动力作用下的响应往往具有非线性特征,对长期响应极值的准确预报通常需要在整个海况域上进行时域非线性数值模拟和统计分析,计算资源耗费巨大。本文采用高斯过程回归和贯序取样技术,设计了机器主动学习的算法,并通过编程开发出了相应的应用模型,实现了基于少数关键海况的分析结果来准确预测长期响应极值的目标。
本文以两型大型集装箱船为算例,采用机器学习模型,对弹性体砰击颤振弯矩和刚体非线性波浪弯矩的长期响应极值进行了预报,结果表明其预测值随着迭代次数增加而快速收敛,在可接受的误差范围内,较传统方法提高计算效率20多倍,达到了工程化应用的程度。对贯序取样结果的分析表明,模型可以很好地识别出对极值响应影响最大的输入区域,显示了机器学习技术的强大功能。
以上机器学习模型中没有引入特定假设,因此具有广泛的适用性,做稍许适应性改造就可以用于其他非线性响应的长期预报。如果将这一机器学习模块嵌入到水动力分析软件中,实现模型迭代结果和水动力计算结果的自动交互,将大幅提高软件的智能化水平和计算效率。
