基于矩阵的并发关系挖掘算法在新冠病毒变异分析中的应用
2023-09-21高胜召陈未如陈章昭
高胜召,陈未如,2,张 雪,2,陈章昭,韩 静
(1.沈阳化工大学 计算机科学与技术学院,辽宁 沈阳 110142;2.辽宁省化工过程工业智能化技术重点实验室,辽宁 沈阳 110142)
0 引 言
新冠病毒变异株中最受关注的是Delta、Omicron、Alpha、Gamma、Beta、Lambda、Mu 变异株。以上变异株或是增加了毒性,或是增强了传播性,某些变异株还会降低疫苗效用,对公共卫生构成重大威胁[1]。因此,对于新冠病毒突变的研究至关重要。
考虑到DNA 序列的特殊性,已经有许多专门针对DNA序列挖掘的算法,如ToMMSA、ATRHunter 等[2]。机器学习也被应用到DNA 序列挖掘[3]。至今已经有许多研究人员在针对SARS-CoV-2 的研究中获得了成果。Qin 等人[4]提出了一种识别共突变模块的算法,并找到了42 个共突变模块,基于这些共突变模块,将SARS-CoV-2 种群分为43 组,并根据不一致的共突变模块的数量确定了各组之间的系统发育关系。Liu 等人[5]提出一种计算并发度的公式。Mishra 等人[6]对SARS-CoV-2 序列进行聚类分析,将突变分为3 类:共同发生的突变、前导和尾随突变、相互排斥的突变。
本文以SARS-CoV-2 为例进行生物变异结构关系挖掘,将共突变模块的挖掘与结构关系模式相结合,提出并发变异关系挖掘,并提出更加适合生物变异结构关系性质的公式,尝试从结构化的角度来挖掘出新冠病毒基因序列的变异信息,并从算法的时间复杂度与空间复杂度进行讨论。
1 结构关系模式挖掘
结构关系模式挖掘是在序列模式挖掘基础上提出的一种新的数据挖掘任务。结构关系是一种包括并发关系、互斥关系、关联关系及这些关系的复合关系的形式,用于表示序列模式之间存在的关系。并发关系[7-9]是指两个或两个以上序列大概率同时出现在同一个大的序列中,也就是说它们都是某几个客户序列的子序列。互斥关系[10]是指两个或两个以上序列大概率不出现在同一个大的序列中。关联关系是指当一个序列出现时另一个序列很大概率也在客户序列中出现[11]。
2 新冠病毒基因序列以及挖掘算法
2.1 新冠病毒基因序列
新冠病毒基因组具有典型的冠状病毒结构,大约含有3 万个核苷酸,核苷酸G 与C 占比约为40%,大约编码9 860 个氨基酸[12]。截至2022 年1 月NCBI(美国国家生物信息中心)上现存两百多万条新冠病毒基因序列。
2.2 变异序列组的构建
为了消除脏数据,便于构建变异碱基矩阵,方便以后的生物变异结构关系挖掘,我们基于选定的基因数据库VGDB,对原有的病毒基因序列组进行处理与简化,构建出变异序列组。在进行DNA 序列挖掘时大部分算法是对整体DNA 序列进行挖掘,挖掘其序列模式[13-14]。由于DNA 序列很长,所以挖掘时间也较长。在此我们提取变异碱基构建变异序列组,只挖掘变异部分,大大缩减了挖掘时间。
定义1 变异序列:在对比病毒基因序列与参考基因序列后,将与参考基因序列不同的碱基(变异点)提取出来,表示为
例1:基因序列为AGGAAC…;参考基因序列为AGCATT…;变异序列为{
定义2 变异序列组:基因数据库中所有基因序列的变异序列构成变异序列组,记为VGDB。
定义3 变异矩阵:储存病毒基因序列碱基变异情况的N×M的01 矩阵,N行代表所有的病毒基因序列,M列代表此病毒基因序列组所有的变异碱基点,0 代表此基因序列不存在这个变异碱基点,1 代表此基因序列存在这个变异碱基点。变异矩阵的构建大大减少了在挖掘中遍历事务数据库VGDB 的次数[15]。
例2:假设的变异碱基矩阵见表1 所列,有S1、S2、S3三条基因序列,有
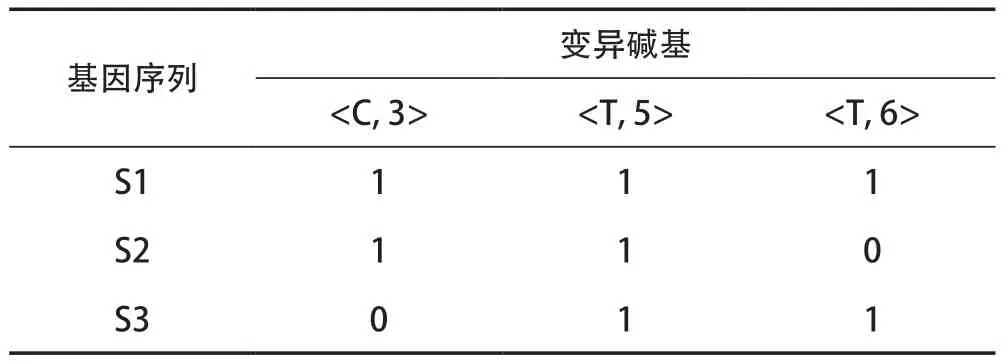
表1 变异碱基矩阵
由此变异矩阵可得基因序列S1 的变异碱基为
变异序列组构建步骤:首先从NCBI 数据库获得新冠病毒基因序列,为了尽可能消除抽样偏差,我们根据抽样日期和国家对序列进行分类。如果基因序列的含糊碱基(未确定是“A”“C”“T”还是“G”,显示为“N”)过长,则删除这些基因序列,这样就获得了新冠病毒基因序列组。然后对新冠病毒基因序列组进行序列对齐,去除对齐后基因组开头和结尾的非编码区[4]。设置一条参考基因序列(参考基因序列应选取比新冠病毒基因序列组日期靠前、株系相近或相同、病毒采取地相同的一条新冠病毒基因序列),将新冠病毒基因序列组与参考基因序列对比,获得变异碱基位点。为了便于表示变异碱基与其碱基位点,提出一种变异碱基点表示形式:
2.3 生物变异结构关系挖掘
生物变异结构关系由三部分组成:并发变异关系、互斥变异关系、关联变异关系。在此我们结合结构关系模式提出以下概念。
定义4 变异率:存在变异点α的变异序列与变异序列组VGDB 序列数之比叫做变异率,记作p(α)。
定义5 共变序列:变异点α1、α2、…、αn在变异序列s中同时存在,即A={α1,α2, ...,αn}是s的子序列,称变异序列A是在s中的共变序列,或称s支持序列A。
定义6 共变率:包含序列A={α1,α2, ...,αn}的变异序列数与变异序列组VGDB 序列数之比,记作p(A)。
定义7 并发度:包含序列A={α1,α2, ...,αn}的变异序列数与存在A中任意变异点的变异序列数之比,称为序列A的并发变异度,简称并发度,记作conv(α1,α2, ...,αn),或conv(A)。
式中,分子是包含序列A={α1,α2, ...,αn}的变异序列数,分母是至少包含A中任一变异点的变异序列数。分子分母各除以变异序列组VGDB 序列数,则分子就是p(A)。
式(3)中分母的计算比较复杂,考虑简化计算,将包含k个变异点的序列称为k-序列。序列A={α1,α2, ...,αn}有n个1-序列、n(n-1)/2 个2-序列、…、n个(n-1)-序列和1 个n-序列,这些统称为A的k子序列。
设序列A={α1,α2, ...,αn}的各k子序列的并发率之和分别表示为p(Ak),k=1, 2, ...,n,则有:
根据容斥原理的性质,式(3)可以改写为:
例3:假设变异序列组为:
则有:
根据式(4),可得:
定义8 并发关系:序列A={α1,α2, ...,αn},对于客户指定的最小并发度minconv,当conv(A)≥minconv 时,称A存在并发变异关系,简称并发关系,表示为[A]=[ɑ1+ɑ2+...+ɑn]。
在例3 中,设minconv=0.5,则有并发关系[
并发关系有如下性质:
(1)性质1:并发关系具有反单调性。若序列A={α1,α2, ...,αn}存在并发关系,则其任意子序列也一定存在并发关系。
证 明:设 序 列A={ɑ1,ɑ2, ...,ɑn} 存 在 并 发 关 系[ɑ1+ɑ2+...+ɑn],即conv(A)≥minconv,A′为A的一个n-1子序列(k≤n)。可知在VGDB 中,包含A的所有序列一定包含A′,所以p(A′)≥p(A)。由于少了一个累计变异点,式(3)、(4)的分母值将变小(至少不变大)。因此,conv(A′)≥conv(A)≥minconv。即存在并发关系的n序列的所有n-1 子序列存在并发关系。依此类推,存在并发关系的序列的所有子序列存在并发关系。反单调性质成立。
为了利用并发关系的反单调性进行并发关系挖掘,定义候选并发关系。
定义9 候选并发关系:若序列的所有子序列都存在并发变异关系,则这个变异序列构成候选并发变异关系,简称候选并发关系。
根据并发关系的反单调性质,任意一个变异序列存在共变关系的前提是其所有子系列存在共变关系,即它首先应该是一个候选并发关系。通过并发变异率矩阵很容易得到所有的二元并发变异关系,然后再以所有的二元并发变异关系为基础组成三元候选并发关系集合,从中筛选出满足条件的三元并发关系。以此类推,可以逐步得到所有并发关系。
定义10 单变序列:变异点α1、α2、...、αn在变异序列s中存在且只存在其中一个点,称A={α1,α2, ...,αn}为在s中的单变序列,该单变序列包含在s中。
定义11 互斥度:包含单变序列A={α1,α2, ...,αn}的变异序列数与存在A中任意变异点的变异序列数之比,称为单变序列A的互斥度,记作 xclv(α1,α2, ...,αn) = xclv(A)。
根据容斥原理的性质,与式(4)类似,将式(5)改写为:
定义12 互斥关系:序列A={α1,α2, ...,αn},对于客户指定的最小互斥度minxclv,当xclv(A)≥minxclv 时,称A存在互斥变异关系,简称互斥关系,表示为[A]=[ɑ1⊕ɑ2⊕...⊕ɑn]。
在例3 中,则有:
设minconv=0.8,则有互斥关系[
定义13 关联度:同时包含序列A和B的变异序列数与包含A的变异序列数之比,称为序列A关联B的关联变异度,简称关联度,记作 assv(A,B)。
定义14 关联关系:对于序列A与B,当A在某一变异序列中出现时B也有很大概率出现,即A与B的关联度assv(A,B)≥min assv(客户指定的最小关联变异度),则称序列A与B满足关联变异关系,简称关联关系,表示为[A→B]。
在例3 中,则有:
若 设minassv=0.9, 则 关 联 关 系[{
3 基于矩阵的并发变异关系挖掘算法步骤
(1)首先通过变异序列组获得此新冠病毒基因序列组所有的变异碱基点集合(allVariationBases)。
(2)然后构建一个N×M的变异矩阵(variationMatrix),N行代表所有的新冠病毒基因序列VGDB,M列代表此新冠病毒基因序列组所有的变异碱基点集合。矩阵的元素为0 或1,0 代表此基因序列不存在这个变异碱基点,1 代表此基因序列存在这个变异碱基点。
(3)首先进行二元并发变异关系挖掘,通过并发度计算公式计算任意两个变异碱基的并发度,将所得结果构建M×M的并发度矩阵(convMatrix),M行和M列均代表此新冠病毒基因序列组所有的变异碱基点。矩阵的元素是公式计算结果。
(4) 由 客 户 指 定 最 小 并 发 度minconv, 当conv(A)≥minconv 时,求得所有的二元并发变异关系。
(5)通过步骤(4)得到的二元并发关系组成三元候选并发关系集合,从中筛选出满足条件的三元并发关系。以此类推,逐步得到所有的并发关系。
4 实 验
4.1 数据选取与处理
从NCBI 数据库上下载日本地区120 条新冠病毒基因序列,根据日期与株系分为3 组,每组40 条,第一组(日期:2020年7月到2021年11月;株系:B.1.1.214),第二组(日期:2021 年1 月到2021 年5 月;株系:B.1.1.7),第三组(日期:2021 年6 月到2021 年9 月;株系:B.1.1.7)。以日本2020年5 月获取的一条B.1.1 病毒序列作为参考序列,将3 组新冠病毒基因序列组与参考序列进行对齐,去除对齐后基因组开头和结尾的非编码区。将新冠病毒基因序列组与参考基因序列对比,获得所有的变异碱基位点,将变异碱基点全部变为
4.2 挖掘并发变异关系
(1)获取3 组的变异碱基点集合:第一组有93 个变异碱基点;第二组有95 个变异碱基点;第三组有156 个变异碱基点。
(2)分别获取3 组的变异矩阵:第一组获得40*93 的变异矩阵;第二组获得40*95 的变异矩阵;第三组获得40*156的变异矩阵。
(3)获取3 组的并发度矩阵:第一组获得93*93 的并发度矩阵;第二组获得95*95 的并发度矩阵;第三组获得156*156 的并发度矩阵。
(4)设最小并发度minconv=0.95,挖掘二元并发变异关系:第一组挖掘到10 个二元并发变异关系;第二组挖掘到276个二元并发变异关系;第三组挖掘到276个二元并发变异关系。
(5) 挖掘多元并发变异关系:第一组挖掘到一个5 元并发变异关系为[
三组之间存在共同并发变异关系:[
4.3 实验结果分析
对本次挖掘结果进行分析:首先,从变异碱基点集合来看,第一组与第二组变异碱基点数量相近,第三组的变异碱基点数量远多于前两组,仅从变异碱基点数量来看,第一组和第二组与参考序列的同源性更高。然后,从并发变异关系来看,第一组挖掘到的并发变异关系数量远远小于后两组,93 个变异碱基点只挖掘到10 个二元并发变异关系,说明在第一组中碱基较少出现并发变异,多为独立变异,变异碱基的普遍度不高。第二组与第三组挖掘到的并发变异关系相同,说明第二组与第三组属于同一株系,再由变异碱基点数量来看,三组数量多,说明三组较二组与参考序列的同源性更低,三组是在二组的基础上变异的。第一组与二、三两组有共同的并发变异关系,说明第一组与第二、三两组属于同一个大的株系。分析实验结果可知,三组株系关系与实际情况相同,符合B.1.1、B.1.1.214、B.1.1.7 之间的亲缘关系。B.1.1.7 曾是值得关注的株系,现为正在监测的株系(新冠病毒关注级别由低至高:正在监测的变种、值得留意的变种和值得关注的变种);B.1.1.214 为普通株系(株系等级由疾病预防与控制中心官网得到);B.1.1.7 的毒性或传播性大于B.1.1.214。
为了避免本次实验存在偶然性,所以我们又从印度选取120 条新冠病毒序列做一个对照实验。根据日期与株系分为3 组,每组40 条,第一组(日期:2020 年7 月到2021 年12 月;株系:B.1.1.306),第二组(日期:2020 年11 月到2021 年1月;株系:B.1.1.7),第三组(日期:2021 年2 月到2021 年5 月;株系:B.1.1.7)。参考序列选取印度2020 年6 月获取的一条B.1.1 病毒序列。第一组获得112 个变异碱基点和6组二元并发关系;第二组获得105 个变异碱基点和359 组二元并发关系;第三组获得153 个变异碱基点和377 组二元并发关系。通过对挖掘出的变异碱基和并发关系进行分析,三组株系属于同一个父株系,二、三组属于同一株系,并且第三组是在第二组的基础上变异而来,符合B.1.1、B.1.1.306、B.1.1.7 之间的关系。B.1.1.7 曾为值得关注的株系,现为正在监测的株系;B.1.1.306 为普通株系;B.1.1.7 的毒性或传播性大于B.1.1.306。
针对日本与印度病毒序列的两组实验的结果大致相同,根据挖掘到的变异碱基与并发关系可以推断出变异序列之间的同源性,所得结果与实际大致相符。本文的实验结果表明,并发变异关系可能是驱动不同株系致病性或传播性的主要进化力量,并且可能是决定这些株系毒性或传播性程度更高和更低的原因。
4.4 算法效率分析
时间复杂度:在求并发变异关系时,时间复杂度主要由构建变异矩阵、构建并发度矩阵、生成候选并发变异关系和对候选并发变异关系计算并发度四部分构成。
构建变异矩阵:假设变异序列组存在m条变异序列,这些变异序列分别与数量为n的变异碱基集合进行比对,时间复杂度为O(mn2)。
构建并发度矩阵:计算conv 需要O(m),需要计算n个变异碱基,由于并发度矩阵是中心对称的,只需计算矩阵的上三角形部分,所以时间复杂度为O(mn)。
生成候选并发变异关系:时间复杂度为O(mn2)。
对候选并发变异关系计算并发度:时间复杂度为O(n2),所以算法总的时间复杂度为O(mn2)。
基于Apriori 的并发变异关系挖掘算法在生成每个候选并发变异关系时,要通过遍历事务数据库来获得并发度,时间复杂度为O(mn2)。因此,当生成ɑ个候选并发变异关系时,基于Apriori 的并发变异关系挖掘算法的要比基于矩阵的并发变异关系挖掘算法多O(ɑmn2)。
比较基于矩阵的并发变异关系挖掘算法(M-alg)和基于Apriori 的并发变异关系挖掘算法(A-alg)对不同数量的变异序列组进行挖掘实际所需时间。结果如图1 所示。
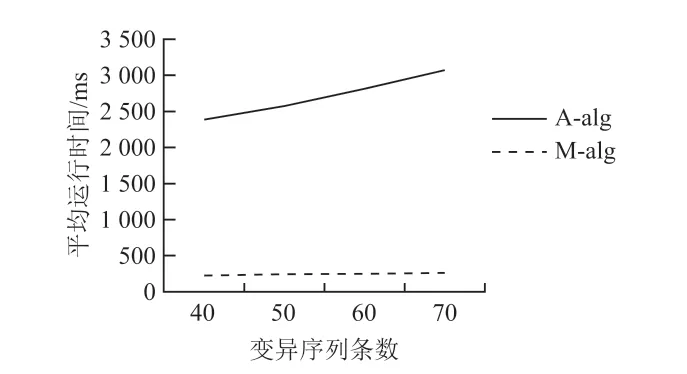
图1 并发关系算法挖掘不同序列条数运行时间比较
由于挖掘对象是变异碱基而不是整条基因序列,并且在最开始将事务数据库转变为变异矩阵,挖掘时只需遍历一遍事务数据库即可,所以挖掘时间较基于Apriori 的并发变异关系算法大大减少。
空间复杂度由两部分构成:(1)变异矩阵:需要一个n*m的二维数组,空间复杂度为O(nm);(2)并发度矩阵:需要一个n*n的二维数组,空间复杂度为O(n2)。因此,算法总的空间复杂度为O(n2)(目前实验数据量:变异碱基数量n与新冠病毒序列数量m的范围均为0 ~200)。就目前新冠病毒变异碱基数量与我们所需要挖掘的新冠病毒序列条数来看用内存来存储完全够用,所以在追求较快运行速度的前提下优先使用内存来存储,在以后挖掘时遇到内存不够时也会选用外存来存储数据。
5 结 语
由于环境和宿主的选择压力,一部分基因一起发生突变,这样就形成了共突变,就相当于本文的并发变异关系。在癌症细胞中存在互斥变异关系,在同一致病通路上的基因只需要变异一个即可以导致功能异常,因此多个基因的变异会使得功能冗余,不具有选择优势[16]。在生物变异的过程中一个基因的变异会导致另一个基因的变异,这就是本文中的关联变异关系。因此,对生物变异的并发变异关系、互斥变异关系、关联变异关系的挖掘是非常有必要的。本文通过挖掘新冠病毒基因序列的并发变异关系,可以判断新冠病毒序列之间的同源性,证明结构关系模式挖掘是可以应用到生物变异信息挖掘的;此外就目前数据规模而言,算法效率是可以接受的。
