优化的K-means 聚类算法在客户细分中的应用研究
2023-09-21唐欣
唐 欣
(北方民族大学数学与信息科学学院, 银川 750021)
0 引 言
互联网技术的快速成长,带动了电商、教育、医疗以及生物科技等领域的不断突破创新,大数据成为生活中不可或缺的一部分,使得交通出行、网上购物、线下支付等一系列活动简便快捷。 信息多元化,数据挖掘与获取信息密不可分,通过数据清洗、转换以及集成等方式来挖掘有效信息。 聚类分析是数据挖掘常用的聚类方法,利用同一类簇相似性高,不同类簇相似性低的行为准则划分数据,市场研究人员也常常将这一方法运用到客户细分中。
20 世纪50 年代中期,美国学者温德尔史密斯根据市场细分准则提出了客户细分的概念[1]。 即基于某一标准,将企业库中的所有客户划分为多种类型的客户群的过程[2]。 利用聚类分析对客户划分的方法,能够挖掘更多有用信息,帮助企业了解客户的消费行为、习惯以及购物偏好等相关信息,达到更好地为客户提供个性化、差异化服务与体验的目的,进而有针对性地制定营销策略,促进公司持续健康发展。
不同的企业往往会制定不同的客户细分准则,挖掘客户特点,建立与客户之间的联系,实现公司利益最大化。 Wang L 等[3]人从生命周期的角度出发,认为客户在生命的不同阶段会产生感知差异,而这种差异往往会带来不同的消费行为;王璀璨等[4]从客户价值的角度出发,优化客户关系管理系统,实现对电商企业的客户细分;Hughes 等[5]从客户行为的角度出发,通过建立RFM 模型(R代表最近一次消费时间、F代表消费频率、M代表消费总金额),了解客户消费行为习惯,做出不同价值分类,为企业更加有针对性地管理提供新思路。 根据八二法则可知,企业的80%利润往往是来自于20%的忠诚客户[2],说明了利用RFM 模型,通过给出不同客户的价值分类,将这部分客户转化为忠诚客户后,他们重复购物能力往往能为企业带来更多的利润来源,而维持这部分客户远远小于获取一个新客户所要花费的成本。
很多学者为了更好地探索客户细分模型,常常利用数据挖掘的手段,结合聚类分析的方法来对客户进行划分。 原慧琳等[6]从微观和宏观两个角度出发,利用K-means 聚类算法对零售会员数据进行特征划分;杨琳等[7]根据民航客户自身特点,结合聚类分析方法,对RFM 模型进行了改进,进一步提高了民航企业的服务质量;闫春[8]等利用轮廓系数改进K-means 选取聚类数目,并在寿险数据中为挽留高价值客户提供了较高的决策依据。 因此,将聚类分析方法应用到不同类型的客户群的划分中,能够帮助企业了解不同客户需求,给出客户价值定位,重新构建客户管理体系,提供个性化服务。 本文将优化的K-means 算法应用到RFM 模型中,实现对客户数据的聚类,并根据聚类结果找出企业库中的忠诚客户,从而有效制定营销策略。
1 相关知识
1.1 K-means 算法
在聚类分析中,K-means 聚类是最常见的一种数据挖掘算法,是由Macqueen 提出来的基于划分的聚类方法[9]。 K-means 算法的聚类速度快,操作简单快捷,但聚类过程也存在一些缺陷,如依赖初始聚类中心的随机选取、极易受异常值影响、聚类结果不稳定等[10]。 该算法通常使用欧氏距离来作为衡量两个对象之间的相似度指标,划分聚类结果,其基本思想是选择任意的k个初始聚类中心,计算出剩余数据对象与聚类中心的欧氏距离,找到距离最近的k- 1 个聚类对象,不断更新迭代聚类中心,直到误差平方和(SSE),即准则函数收敛,得到聚类结果,表示为C={C1,C2,…,Ck}。
假设有n个m维属性的数据集U∈{xp}(p=1,2,…,n),记ci(i=1,2,…,k)为k个聚类中心,每个聚类中心ci都有m维属性,记为cij(j=1,2,…,m),则每个对象xp距离每个聚类中心ci的欧式距离定义为式(1):
误差平方和定义为式(2):
1.2 优化的K-means 算法
K-means 作为无监督学习算法的一种,不需要提前知道聚类类别,能够对无标识的对象进行聚类。利用欧氏距离做相似度度量指标,得出相同一类簇的距离越小,其相似度越高;不同类簇的距离越大,其相似度越低。 该方法在聚类过程中会因为受到极端值的影响而改变类簇的紧密性与离散性,降低整个聚类的准确性。 本文从样本间的关系出发,首先采用高密度代替距离均值的方式,利用公式(3)计算最近邻密度选取数据集中样本密度较高的点作为第一个初始聚类中心c1,将其余对象划分到已确定聚类中心的类别当中。
其中,xp(p=1,2,…,n) 表示n个m维数据集。
其次,在剩下的没有被划分类别的对象中,采用欧氏距离,利用公式(4)和公式(5)找到离c1最远的下一个临时聚类中心点ck并聚类:
其中,Denλ(xpi,ci) (pi=1,2,…,ni) 表示与聚类中心ci距离小于λ的所有数据对象;ni表示Denλ(xpi,ci) 中的对象数目;A为任意正常数。
λ的计算公式为
利用公式(7)计算该临时聚类中心的密度,搜索距离其密度平均值最近的数据对象作为更新的聚类中心;如此迭代,直到得到所有初始聚类中心。 得到所有数据对象的二支聚类结果,表示为
K-means 聚类算法通常是任意选取k个聚类中心,通常带有一定的随机性。 本文提出了一种优化选取初始聚类中心的方法,利用样本分布信息,选择密度最高的点作为初始聚类中心,有效解决了人为因素干扰或者极端值影响导致聚类陷入局部最优的问题;限制聚类对象在λ的范围内,更加精准地远离了噪声点的干扰;最终聚类结果中能够满足同一类簇的相似程度最高,不同类簇的相似程度最低的条件,确保了聚类的稳定性。
2 优化的K-means 算法的实验验证
实验环境:Intel,CPU16 GB 内存,512 GB 固态硬盘,Windows10 操作系统,开发工具是Python3.8。
2.1 数据集选取
本文从UCI(University of CaliforniaIrvine)数据集中选取了5 组真实数据集,实验数据集描述见表1。
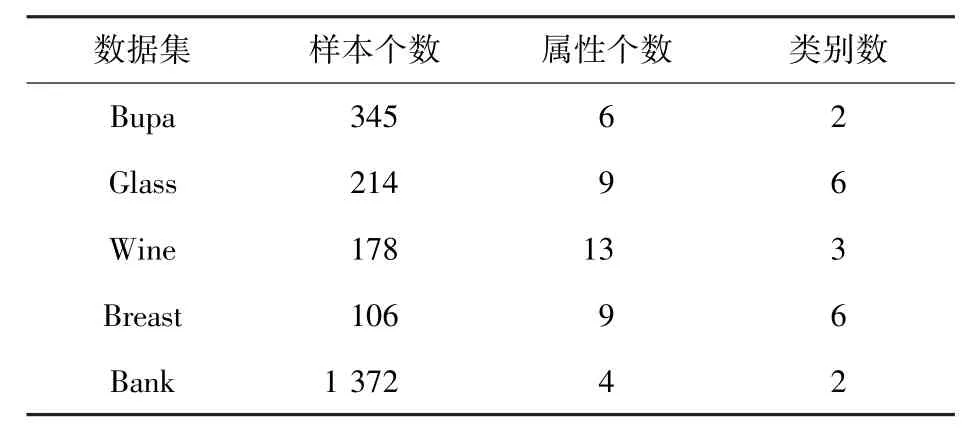
表1 实验数据集描述Tab. 1 Dataset description of experiment
2.2 实验结果与分析
在实际聚类的过程中,为了确保数据的准确性,在聚类之前对数据均采取了无量纲化处理。 同时,本文利用两个聚类有效性指标:内部指标Davies-Bouldin-Index(DBI)及外部指标Accuracy(ACC),验证本文提出的优化后的K-means 算法的聚类有效性。 DBI 指标是通过数据对象之间的紧密程度和分离程度来判断其内部结构和分布状态,DBI 越小,说明同一类的相似性越高,不同类的相异性越高;ACC 指标是比较最终聚类结果与数据集原始真实标签值,从而判断数据的准确性。 实验结果见表2,
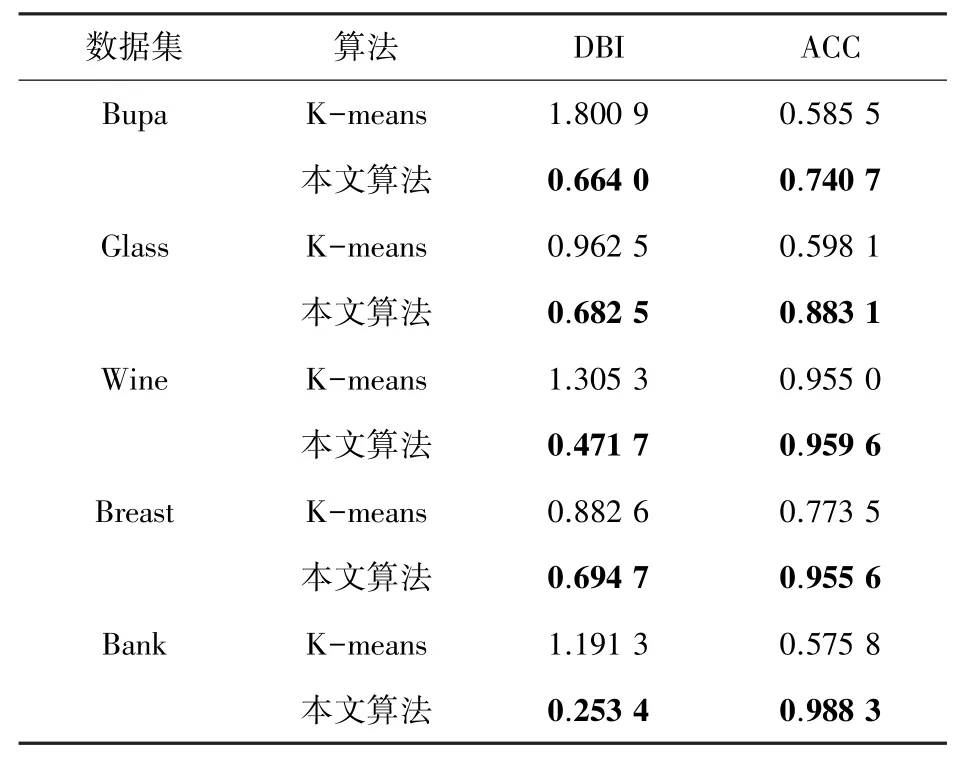
表2 UCI 数据集上的实验结果Tab. 2 Experiment results of UCI dataset
由表2 可知本文算法在数据集上拥有更小的DBI,说明优化后的K-means 算法同一类簇之间的紧密性高,不同类簇之间的分离性高;同时,本文算法在数据集上均拥有了较高的准确率,聚类效果较好。 说明表明优化的K-means 聚类算法更具有有效性,将其应用到客户细分模型中去,可实现更好的聚类结果。
3 优化算法在客户细分中的应用
3.1 模型构建
本文利用Kaggle 竞赛平台中下载的2011 ~2014 年全球消费数据样本“Global Superstore”,选择了5 191条美国“Business-to-Customer”领域的消费数据,消费时间为2011 年1 月4 日至2014 年12 月31 日。
首先,将数据进行预处理。 对给出的5 191条消费者数据进行订单编号、日期、金额等指标进行筛选,样本均在正常范围内,无异常数据。
其次,创建RFM 模型,得到一份只含有R、F、M3 个指标409*3 的消费者数据(其中,R表示消费者最近一次交易时间距离2014 年12 月31 日的天数,F表示消费者在这4 年内的消费总频次,M表示消费者在这4 年内的消费总金额),部分数据见表3。
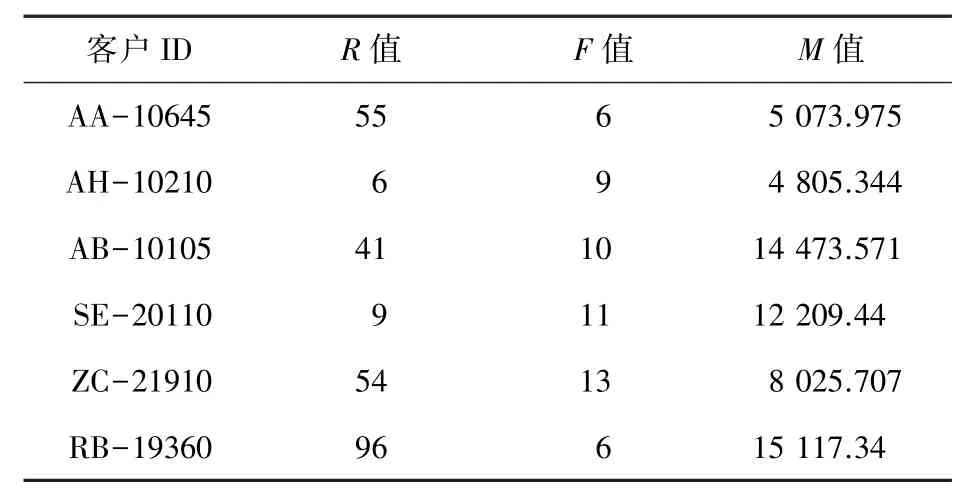
表3 消费者的RFM 指标数据(部分)Tab. 3 The RFM indicator data of consumers(partly)
对409 位消费者数据的RFM 模型进行描述性统计分析见表4。
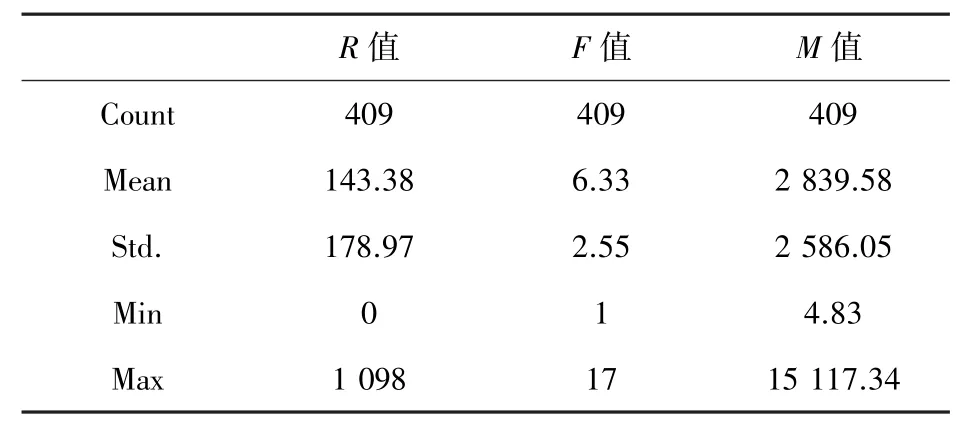
表4 消费者的描述性统计Tab. 4 Descriptive statistics of consumption data
通过表4 可知,R、F、M3 个指标之间存在较大的差异性,为了避免3 个指标的量级不同而影响到聚类结果,本文采用“Z-core 标准化”的方式处理数据,降低不同指标之间的差异,确保指标之间的变量具有可比性,标准化后的消费者的RFM 数据见表5。
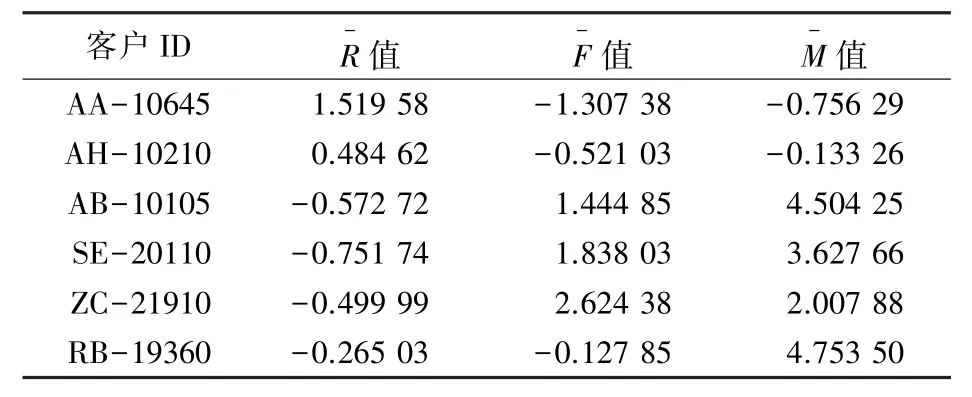
表5 标准化后消费者的RFM 数据(部分)Tab. 5 The RFM indicator data of standardized consumers(partly)
3.2 聚类效果分析
用优化的K-means 算法对全球消费者数据进行聚类,将这409 位消费者聚成4 类,聚类结果见表6。 根据这4 个客户群来划分客户类型,分别表示为核心客户、保持客户、一般客户以及挽留客户4 种。
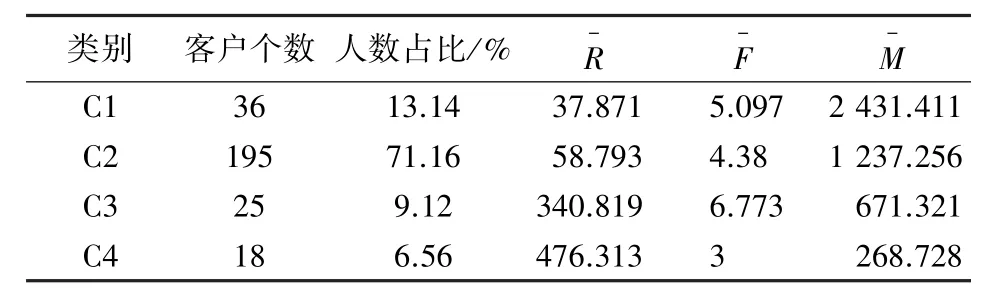
表6 优化后的K-means 算法的消费者聚类结果Tab. 6 Consumer clustering results of optimized K-means algorithm
C1 为核心客户,对于企业来说,这类客户有较高的忠诚度,虽然人数不多,仅仅占整个人数的13.14%,但是平均消费频率快,间隔次数短且消费金额高,是对企业发展贡献最多的一类客户。 企业需要抓住这类核心客户,多与客户沟通,时刻关注其购物需求,提供最大品牌优惠力度,开通特殊服务通道,推送有买有送的小礼品赠送服务,提升其购物体验,保证核心客户始终对企业有较高的满意度。
C2 为保持客户,人数在企业中的占比最多,占到了企业的2/3,但是消费水平处于一个比较居中的状态,在RFM 模型中,虽然、值不如核心客户C1,但其平均消费频率更高,综合来看依旧能保持在一个相对较好的消费水平。 因此企业应该尤为关注这类消费者,进行问卷调查,了解其消费偏好,及时调整企业自身存在的不足,并为其推出商品打折、满减、优惠券等活动,促进其购买意愿,缩短消费间隔,增加消费频次,可以将部分客户转化为忠诚客户,减少这类客户的流失。
C3 为一般客户,这类客户最终的RFM 模型中的3 个指标均不如C1 和C2,但是从来看,他们的消费能力并不算太差,说明其购买行为存在较大的随意性,属于冲动型消费人群,可能在遇上如年中大促等大型活动时才会产生较高的购买意愿。 因此,企业应该减少对这类客户的资源投入,减少维护成本,在公司商品促销、降价等活动中,利用短信、公众号等渠道进行推送,吸引消费。
C4 为挽留客户,这类客户平均最近一次消费的时间有一年多,对于企业来说创造收益的价值较少,但是其人数占据总人数的6.56%,可能是新用户,应该把握其消费取向,调整相关营销策略,适当减少其消费间隔,吸引消费。
4 结束语
本文利用样本间的分布,采用密度与距离两者相结合的方法优化了K-means 聚类算法,通过聚类有效性指标验证了该算法的有效性;将优化的Kmeans 算法应用到客户细分模型中,并由此得出结论:留住高价值客户,提高其对品牌的忠诚度;放弃低价值客户,节省企业成本。
本文的算法在提高聚类准确率的同时,为企业分析客户群提供了一种新的聚类方法,帮助其精准定位,有效营销,具有一定的现实意义。 然而,如今的客户细分的标准也开始呈现多样性,不再局限于单一的RFM 模型。 因此,接下来将从数据特征出发,探究更多的划分标准。
