基于小波软阈值滤波的含噪故障诊断方法
2023-09-21田奥升陈慧玲
田奥升, 张 晔, 马 超, 陈慧玲
( 国防科技大学电子科学学院, 长沙 410073)
0 引 言
为了保证设备安全稳定运行,减少造成经济损失的安全事故,智能故障诊断在工业领域得到了广泛的应用[1]。 然而,复杂环境下采集到的信号通常含有大量噪声,这些噪声严重干扰了机械故障诊断的特征提取,导致了故障诊断性能的下降,因此研究有效的抗噪故障诊断方法具有重要意义。
目前,故障诊断方法主要分为基于手工特征的方法与基于深度特征的方法两类。 基于手工特征的方法需要两步操作。 首先,提取最大最小值、平均值、方差和信息熵等手工特征;其次,利用支持向量机、随机森林、决策树等传统分类器对手工特征进行分类[2]。 基于深度特征的方法利用深度神经网络模型从故障信号中自动提取特征并完成分类。 目前,在机械故障诊断领域,基于深度特征的方法因强大的特征提取能力已成为主流[3]。
近年来,学者们将深度学习方法广泛应用于故障诊断领域。 文献[4-5]将卷积神经网络(CNN)用于故障诊断;文献[6]提出了一种用于旋转机械故障诊断的多级融合双卷积神经网络(MFDCNN),实现了故障信息的多层次融合;文献[7]提出了一种紧凑的一维卷积神经网络(1DCNN)故障诊断方法,能够自动从背景噪声中提取有效特征;文献[8]提出了一种多注意力一维卷积神经网络(MA1DCNN),用于轴承故障诊断,能自适应地对各层特征重新校正,增强了故障脉冲的特征学习能力;文献[9]提出了一种基于CNN 的故障诊断模型,将一维振动数据直接转化为二维图像,利用CNN 提取不同故障图像的特征进行故障诊断。 虽然这些方法取得了较大的成功,但是常用的CNN 网络对高频噪声很敏感[10]。 噪声的干扰可能会干扰到相关特征的提取,进而限制网络性能的提升。 而在复杂环境下采集到振动信号通常含有大量噪声,这对故障诊断提出了新的要求与挑战,因此研究抗噪机械故障诊断方法具有重要意义。
本文提出了基于小波软阈值滤波的残差网络(WSTResNet)。 首先,利用深度残差网络提取有效特征;其次,利用小波变换下采样来减弱高频噪声的影响;最后,对小波特征进行软阈值滤波操作,进行进一步的去噪处理。 通过小波软阈值滤波处理来增强深度残差网络对含噪振动信号的特征提取能力,实现噪声环境下较高的故障诊断性能。
1 基于小波软阈值滤波的残差网络
1.1 网络总体框架
本文提出的基于小波软阈值滤波的残差网络由多个小波软阈值滤波模块组成,具体结构如图1 所示。 小波软阈值滤波模块通过小波变换与软阈值滤波实现。 首先,将原始信号输入到卷积层与小波变换层来获取小波特征;其次,小波特征被送入多层小波软阈值滤波模块,对小波特征进行去噪处理;最后,全局池化后的特征通过线性分类器来获得最终的故障类别。

图1 基于小波软阈值滤波的残差网络结构Fig. 1 The structure of residual network based on wavelet soft threshold filtering
1.2 残差网络
卷积神经网络具备优异的特征提取能力,因此被广泛运用于故障诊断[11]。 由于网络的加深会产生梯度消失,因此随着层数的增加,网络的性能并未得到提高。 为了处理这一问题提出残差结构,其结构如图2 所示。 残差神经网络的输出函数,如式(1)所示:
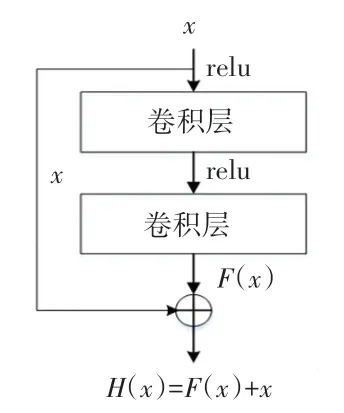
图2 残差结构Fig. 2 Residual structure
其中,F(x) 是卷积层输出特征,x是输入卷积层前的特征,当F(x)=0 时,即变为恒等映射。
残差结构更易于网络训练,也能够提高网络的泛化性能,更适合于深度网络的构建。
本文利用深度残差网络来提取深度特征,深度残差网络总共有6 层残差模块,每一层残差模块的卷积核大小均为3,其具体结构见表1。

表1 网络结构Tab. 1 Structure of network
1.3 小波软阈值去噪
小波软阈值滤波是一种常用的信号去噪方法。小波阈值去噪方法分为3 个步骤:小波分解、阈值处理和小波重构。 本文只运用了小波分解与阈值处理两个操作。
1.3.1 离散小波变换
得益于小波变换强大的时频分析能力,小波变换在故障诊断任务中得到了广泛应用[12]。 小波变换是将信号变换到不同尺度的小波系数上,本文采用离散小波变换来增强网络的特征提取能力。 低频成分xL[n] 分解过程如式(2)所示:
其中,x是原始信号。
高频成分xH[n] 分解过程如式(3)所示:
其中,h[n] 是高通滤波器。
在深度小波残差网络中,本文只保留xL[n],不仅能够实现时频特征的提取,还能够减少数据计算量,完成下采样。 小波下采样能够有效地降低高频噪声的影响,同时也能够保留更多的细节信息。
1.3.2 软阈值滤波
在小波域中,有效信号对应的系数很大,而噪声对应的系数很小,因此可以利用小波阈值滤波来减弱噪声干扰。 小波阈值去噪方法分为硬阈值法与软阈值法。 硬阈值法是将小于阈值的小波系数赋零,其余部分不变;而软阈值法是将小波系数大于阈值的部分减去阈值[13]。y为输出特征,阈值τ通过网络学习,软阈值函数如式(4)所示:
其中,x为输入特征,τ为阈值。
为了增强网络的抗噪能力,本文将软阈值滤波与深度网络相结合,使其能够适应不同程度的噪声干扰。 小波软阈值滤波结构如图3 所示,小于阈值的点赋零,大于阈值的点与阈值作差。 通过构造软阈值支路,使网络能够自适应地学习阈值,从而适应不同程度的噪声干扰,有效增强了网络的鲁棒性。
软阈值的实现过程如图4 所示。 首先,对输入x进行全局池化操作降维;其次,将获得的一维向量输入到全连接层中,得到阈值;最后,利用sigmoid 函数对得到阈值进行约束,使其大小位于(0,1)中。

图4 软阈值滤波的实现过程Fig. 4 The realization of soft threshold filtering
2 验证与分析
2.1 实验环境设置
操作系统: windows 10, GPU: NVIDIA RTX 1080Ti,深度学习框架:Pytorch 1.7.1。
2.2 CWRU 数据集
CWRU 数据集由凯斯西储大学轴承数据中心提供。 振动信号是在4 种不同的轴承载荷(0~3hp)下由驱动端和风扇端的加速度计采集。 其中每个轴承载荷包含3 种主要故障类别:滚动元件、内滚道和外轴承滚道,每个故障类别还包含3 种故障直径即0.007 英寸、0.014 英寸、0.021 英寸。 因此,每种工况下轴承的状态有十种。 CWRU 数据集的详细信息见表2。
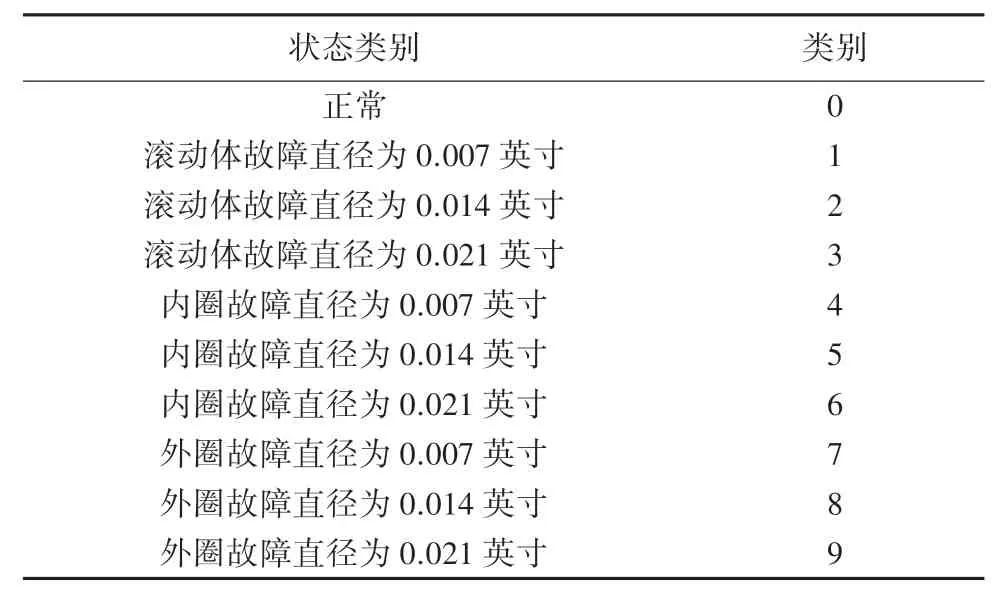
表2 CWRU 数据集的详细信息Tab. 2 The details of CWRU datasets
2.3 实验数据处理
首先,将原始数据滑窗分割处理,窗长为1 024,没有重叠;其次,对所有样本进行最大最小归一化处理;最后,所得到的数据集的样本总数为3 000,选取2 100个样本作为训练数据集,900 个样本作为测试数据集。
2.4 模型训练设置
在模型训练过程中,使用交叉熵损失函数与Adam 优化器。 训练的初始学习率是0.01,训练学习率随训练次数的增加而下降,训练的迭代次数是200,batch size 是64。 采用五折交叉验证评估模型的性能。
2.5 实验结果及分析
为了验证模型的抗噪性能,实验在原始数据中添加不同信噪比(SNR) 的高斯白噪声来验证方法的抗噪性能,如式(5)所示:
其中,Ps是信号的能量,Pn是噪声的能量。
将本文方法(WSTResNet)与CNN、LeNet、MLP、ResNet 4 种方法进行分类准确率对比,实验在-10 dB、-5 dB、0 dB、5 dB、10 dB 5 个不同信噪比下进行,实验结果见表3。
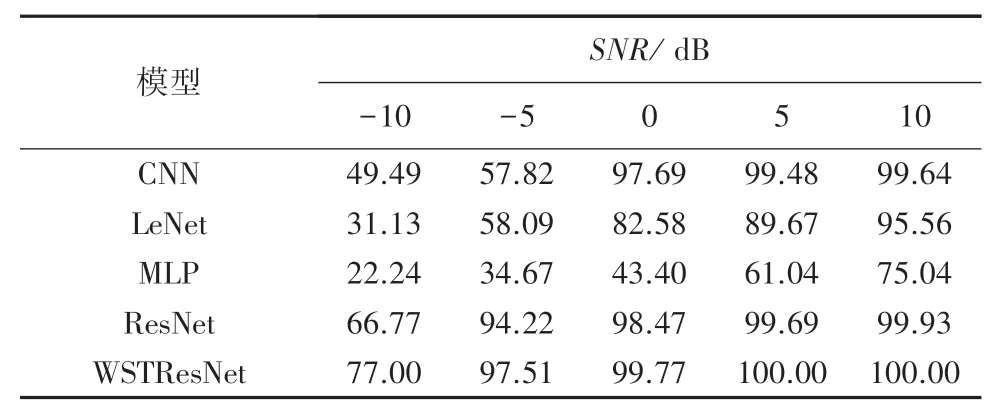
表3 不同信噪比下的算法准确率比较Tab. 3 Comparison of algorithm accuracy under different SNR %
从表3 中的实验结果可知,相比较于其他方法,本文的方法在不同信噪比下能取得更高的准确率,具备更有效的抗噪能力,有效增强网络的抗噪能力。
3 阈值有效性分析
本文对不同信噪比下的阈值进行了统计与分析,统计了测试集样本在每一层残差模块的阈值平均值,不同信噪比下的软阈值分布如图5 所示。 从图5 可知,信噪比越低,阈值整体偏高,表明软阈值滤波在一定程度上能适应不同水平噪声的干扰;另外,随着网络的加深,阈值逐渐下降,表明软阈值滤波能够有效地减少噪声的干扰。
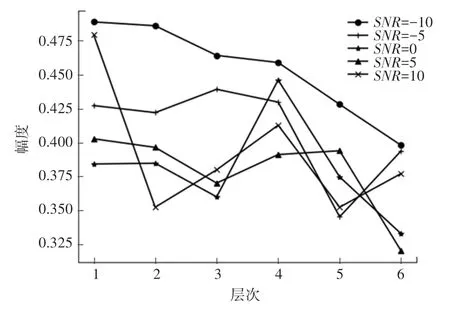
图5 不同信噪比下的软阈值分布Fig. 5 The distribution of soft threshold under different SNR
4 结束语
本文将小波软阈值滤波方法融入深度残差网络,来增强网络的抗噪性能。 在不同信噪比的CWRU数据集下的实验结果表明,基于小波阈值滤波的深度残差网络具备更好的抗噪性能。
但本文提出的方法在数据自适应方面存在不足:固定小波基难以做到数据自适应;虽然软阈值滤波能做到实现可学习阈值,但是阈值滤波函数有待优化。
