自适应惯性权重优化的粒子群算法
2023-09-21王贤琳
张 豪, 王贤琳
(武汉科技大学机械自动化学院, 武汉 430081)
0 引 言
粒子群算法(Particle Swarm Optimization, PSO)是由美国学者Kennedy 和Eberhart 于1995 共同提出的,通过对鸟群捕食习惯仿真,利用群体和个体之间信息共享达到捕食的目的,作为智能启发式算法之一,具有操作简单、参数少、易实现等优点[1]。 许多学者对粒子群算法进行改进,以加强粒子群寻优性能。 文献[2]首次提出粒子群惯性权重,惯性权重取0.9~1.2 时,粒子群具有较好的性能;文献[3]提出线性递减惯性权重,惯性权重线性下降时,粒子群在运行时可能缺乏全局搜索能力。 近年来,为了提高粒子群算法的稳定性,研究人员主要从惯性权重、学习因子和粒子群拓扑关系分析展开研究。
惯性权重是粒子群算法的核心参数之一,影响着算法的收敛性。 为了加强算法稳定性,改善收敛能力,文献[4]提出惯性权重一定时,粒子具有较好的收敛性,但是此方法在高维测试函数上求解较弱;文献[5]提出了正态分布衰减惯性权重粒子群优化,使得算法能很好的平衡全局搜索和局部搜索能力;文献[6]对粒子运动状态实施动态监测,并实时调整粒子惯性权重,大大减少粒子无效迭代次数;文献[7]赋予每个粒子每一维度以不同的线性衰减混沌化惯性权重,够较大幅度地增强粒子群算法的搜索能力,提高算法的寻优精度。
本文提出一种自适应惯性权重优化的粒子群算法(Adaptive Particle Swarm Optimization,APSO),将惯性权重和迭代次数以及每个粒子适应度联系起来,自适应的调整粒子群体中各粒子的惯性权重,改善算法性能。
1 基本粒子群算法(PSO)
粒子群算法在D 维空间中将每个粒子当作空间中的一个点,在求解过程中粒子不断迭代更新改变位置,直到找到最优解,粒子i的位置和速度迭代如公式(1)和公式(2),位置与速度皆为向量。
其中,w为速度的惯性权重;c1,c2为加速因子,一般取值为2;r1,r2为0~1 的随机数;vdi为粒子上一轮迭代的速度;为社会学习向量;gbestd-为个体学习向量。
2 自适应惯性权重粒子群算法(APSO)
惯性权重是粒子群算法很重要的参数,惯性权重一般取值2,对于取定值的粒子群算法,收敛效果并不理想。 文献[3]最先加入惯性权重,并分析指出一个较大的惯性权值有利于全局搜索,而一个较小的权值则更利于局部搜索。 为了使粒子群算法更稳定,对粒子群算法惯性权重采取自适应变化,与原始粒子群算法相比,现在惯性权重和迭代次数与每个粒子适应度有关。 对于最小值问题,惯性权重变化规则如式(3);对于最大值问题,惯性权重变化规则如式(4)。
其中,wmin和wmax为预先给定的最小惯性系数和最大惯性系数,一般取0.4 和0.9。
第d次迭代时所有粒子的平均适应度,式(5):
第d次迭代时所有粒子的最小适应度,式(6):
在每次迭代寻优时,总有部分粒子找到更优的位置,也有部分粒子在较优和较差的位置,在结束此次迭代进行下次迭代时,那些处于越优位置的粒子会进一步达到更优的位置,而在较差位置的粒子会越来越差。 经过不断迭代,越优位置的粒子会更接近或达到全局最优位置。 每次迭代更新时,依据上次迭代粒子的适应度值,在下次迭代时动态调整惯性权重,对粒子全局寻优和快速收敛有很大帮助。
自适应惯性权重粒子群算法流程:
(1)初始化粒子,设置群体规模N,最大迭代次数T,包括粒子的速度和位置,给出个体学习因子和社会学习因子;
(2)计算每个粒子适应度,将单个粒子的最优位置和群体粒子的最优位置分别记为和pbestd;
(3)算法是否收敛,若是,则直接输出pbestd,否则进入下一步;
(4)通过式(7)计算粒子i在第d次迭代后的适应度值变化:
其中,i=1,2,…,n,t≥2;f() 表示粒子i在第d次迭代后的适应度值;
(5) 根据式(3) 动态调整惯性权重;
(6)根据式(1)和式(2)更新粒子群体速度和位置;
(7)重新计算粒子适应度,存储和pbestd,并跳转到步骤(3);
(8)输出群体最优适应度pbestd,运行结束。
3 仿真试验
3.1 测试函数
为了验证自适应惯性权重粒子群算法的有效性,将固定权重的粒子群算法与自适应惯性权重优化的粒子群算法进行性能比对分析。
Sphere 函数为典型的单峰函数,仅有一个极值点;Rosenbrock 具有一个全局最小值点,但其为病态函数, 一般算法难以求得最优解; Rastrigin 和Griewank 为多峰函数,解空间具有多个局部最小值点。 各测试函数的函数表达式、维数、取值范围、理论极值和误差目标见表1。

表1 标准测试函数及其参数Tab. 1 Standard test function and its parameters
3.2 参数设置
对于基本PSO 算法,权值固定w=0.9,c1=c2=2;APSO 算法权值wmax=0.9,wmin=0.4,c1=c2=2.05;对于这两种算法,粒子数量都设置为1 000,变量个数为30,每次求解过程算法迭代的最大次数为1 000 次。
3.3 实验结果
每个算法对每个测试函数独立运行30 次,各个函数的适应度及运行时间见表2、表3。
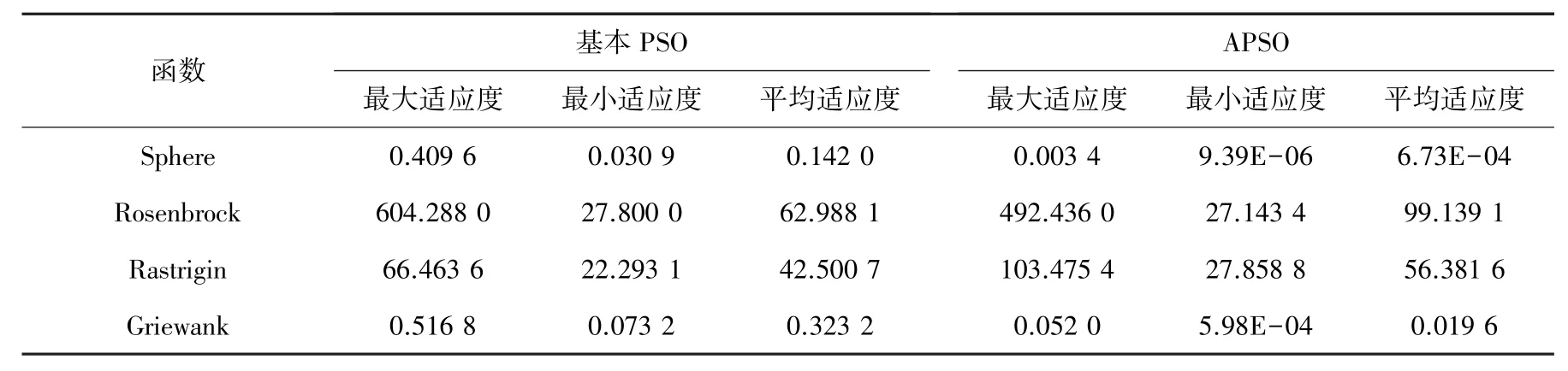
表2 各个函数适应度结果对比Tab. 2 Comparison of fitness results of each function
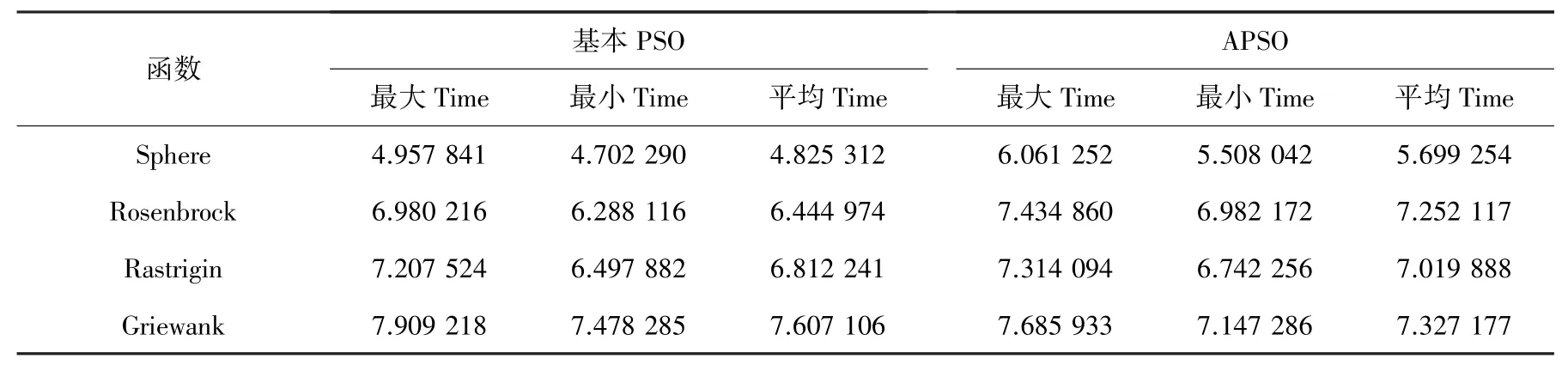
表3 各个函数运行时间(Time/s)结果对比Tab. 3 Comparison of run time ( Time/s ) results by function
从表2 可以看出粒子群算法在对Sphere 函数和Griewank 函数寻找最低值时明显优于Rosenbrock函数和Rastrigin 函数,无论是基本PSO 还是APSO算法,对于Sphere 函数和Griewank 函数,其平均适应度小于1,而对于Rosenbrock 函数和Rastrigin 函数,其平均适应度在40~100 之间,表明在测试函数Rosenbrock 和Rastrigin 上,具有不稳定性。 对于基本PSO 和APSO 两种算法,在测试函数Sphere 和Griewank 上也可以看出APSO 明显优于基本PSO算法,例如Sphere 函数中,基本PSO 算法的平均适应度为0.142 0,APSO 算法的平均适应度为6.73E-04。 至于Rosenbrock 函数和Rastrigin 函数,APSO的平均适应度稍大于基本PSO,也进一步说明粒子群算法优化的不稳定性。
见表3,Sphere 函数较为简单,平均运行时间最短,基本PSO 为4.825 3,APSO 为5.699 2,均小于其他函数平均运行时间。 对于所有的测试函数,APSO算法的运行时间全部大于基本PSO 算法,说明APSO 算法的惯性权重为自适应变化,优化性能更好,优化时间也较长。
为了更加清楚的看到两种算法的收敛性,对测试函数进行收敛性分析,采用基本PSO 和APSO 算法分别求解4 种测试函数成功收敛时的平均最优适应度下降曲线如图1 所示,可以看出两种算法在探索阶段均可实现有效搜索,其中APSO 算法的平均适应度相比于基本PSO 算法下降较快,迭代次数也明显少于基本PSO 算法。
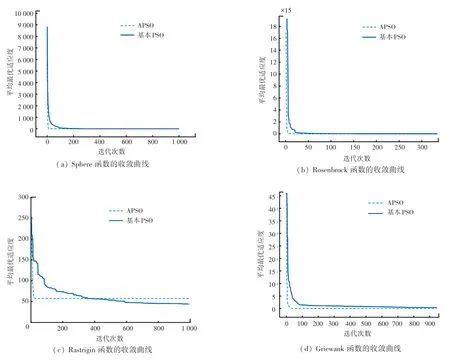
图1 测试函数收敛曲线对比图Fig. 1 Test function convergence curve comparison diagram
4 结束语
为了改善传统PSO 算法的收敛性能,本文提出一种自适应惯性权重优化的粒子群算法APSO,惯性权重采取自适应变化,与每个粒子的适应度有关,该算法简单,推广性强。 对Sphere、Rosenbrock、Rastrigin 和Griewank 4 个函数进行验证,结果表明APSO 算法在Sphere 和Griewank 函数上有较好的效果,其最小值分别为6.73E-04 和0.019 6,精度大幅提高,APSO 明显优于基本PSO 算法。 但APSO 具有一定的不稳定性,后续也可与其他方法融合以提高算法稳定性。
