基于流量时间序列的社交网络事件聚类分析

刘 静， 张 鸽

（山西农业大学软件学院， 山西 太谷 030801）

0 引 言

社交网络是一个用户可以即时发布内容、分享信息并与他人进行交流互动的互联网平台，例如微博、推特等平台。 社交网络上每时每刻都会产生用户发布的大量内容，表现出丰富的时间动态性。 由于社交网络中个体用户行为难以预测，因此分析用户行为非常复杂。 但一些研究表明，互联网在线内容的流量模式可以反映群体用户的行为［1-2］。 事件随时间变化的流量时间序列可以显示出用户群体何时对事件产生关注度，以及关注度如何随时间增长消退的变化模式。 对于某种类型的事件，群体用户的流量时间序列往往会形成一些特定的规律。

现有研究大多根据社交网络中的流量模式分析用户的行为，文献［3］根据用户在电商平台购买及评论的时间序列分析用户的消费行为习惯；文献［4］通过用户行为的时间序列分析来检测社交网络中的欺诈行为。 而本文旨在利用事件的流量模式对事件进行聚类分析。 具有共性特征的事件可能会呈现出相似的流量时间序列，可以根据事件的流量时间序列对事件进行聚类，找到事件的共性特征。 Kmeans 算法是聚类领域最常使用的聚类算法，该算法通过在每次迭代中交替执行簇分配步骤和簇中心更新步骤，来最小化簇内样本到簇中心的距离平方，以找到最终的簇划分结果［5］。 但该算法通常运用在数值型数据上，无法在时间序列数据上体现出数据的时序性；K-SC 算法是一种在K-means 算法基础上改进的，针对时间序列数据进行聚类的算法，用来揭示在线内容时间动态性的规律［6］。 该算法与K-means算法流程相同，都是交替执行簇分配步骤和簇中心更新步骤，只不过根据时间序列数据的特点重新定义了距离和簇中心。 本文利用K-SC 算法对社交网络上热门事件的流量时间序列进行聚类分析，发现具有相似流量模式的事件的共同特征，并分析同类事件流量时间序列的共同特点。 首先需要获得事件的流量时间序列，而确定事件的主题标签是获得事件流量时间序列的关键，本文利用皮尔逊相关系数来确定事件的主题标签，利用事件的主题标签每隔固定时间检索出包含该主题标签的推文，并计算推文数量，该数量形成的序列即为该事件的流量时间序列。 然后就可以利用K-SC 算法对多个事件的流量时间序列进行聚类，找到具有相似时间序列形状的事件，并分析其共性特征。

利用推特上2020 东京奥运会期间场地自行车比赛事件的推文数据进行实验，获取事件的流量时间序列，并对其进行聚类分析，验证了本文方法可以对基于流量时间序列的社交网络事件进行有效聚类，从而发现同类事件的共性特征。

1 方法描述

1.1 获取事件的主题标签

社交网络平台上的事件是用主题标签来确定的，因此找到每个事件的主题标签是检测事件流量模式的关键。 首先，根据事件最关键的主题标签获取包含该主题标签的推文；然后，查看这些推文中包含其他哪些主题标签，并将所有主题标签保存到一个初始标签池H中，记为H＝ ｛H1，H2，H3， …，Hn｝，其中n为当前主题标签的个数。 然而，并非H中的所有主题标签都能直接与某个特定事件相关联，因此使用皮尔逊相关系数对H中的主题标签进行重新检查。 首先，从H中选择那些必定与事件相关的主题标签，如事件的名称，并将其保存到标签池R中，且R∈H；然后为了确定H中的各个主题标签是否与事件相关，需要将其逐个与R中的主题标签进行比较，计算H中每个主题标签与R之间的皮尔逊相关系数。 如果相关性大于某个阈值，则来自H中的某个主题标签被认为是与事件相关的，并保留在H中；如果相关性小于阈值，则将其从H中删除。 计算了相关性后， 最终的H＝｛H1，H2，H3，…，Hm｝（其中m≤n）被视为事件的主题标签。

1.2 创建事件的流量时间序列

获取到每个事件的主题标签H后，就可以根据主题标签来计算事件流量随时间变化的流量时间序列。 每隔一定时间t，包含H的推文总量被认为是该事件的流量，但在H中可能会存在一些噪声主题标签与H中真正的主题标签非常相似但又不属于该主题。 为了减少噪声，需要确保那些包含与H相似的噪声主题标签的推文不被收集。 首先按照目标时间间隔查询数据库，收集与H相似但不包含在H中的主题标签，结果集记为h；然后，在目标时间间隔t上选择包含H但不包含h的推文，记录每隔t分钟的推文数量， 该事件即可获得一个离散的时间序列Ei（mt）（其中m＝1，2，3，…，M，M为时间序列的长度），即事件i在以t为时间间隔的mt时刻上被提及的次数，这个离散的时间序列即为事件的流量时间序列。

1.3 利用流量时间序列对事件进行聚类

获取了社交网络中事件的流量时间序列后，根据流量时间序列对事件进行聚类。 本文利用经典的K-SC 算法对事件的时间序列进行聚类。 K-SC 算法通过在每次迭代中交替执行两个步骤，即簇分配步骤和簇中心更新步骤，来最小化簇内样本到簇中心的距离平方和，即式（1）：

其中，K为簇的个数；Ck为第k个簇的样本集合；d（Ei，μk） 为时间序列Ei到簇中心μk的距离。

K-SC 算法将时间序列样本到簇中心的距离定义为式（2）：

其中，αi为用于匹配两个时间序列形状的缩放系数，Ei（qi）为将时间序列Ei平移qi个时间单位的结果，使得Ei和μk在相同的时间达到峰值。

在K-SC 的算法流程中，首先随机选择K个初始样本作为簇中心；在簇分配步骤中，将每个样本分配到与簇中心距离最近的簇；在簇中心更新步骤中，新的簇中心应该使得对于所有样本的d（Ei，μk）的和最小，即式（3）：

经过推导可得出公式（4）：

其中：

因此求解等价于求解矩阵M的最小特征向量。 根据上述迭代步骤，K-SC 的算法流程见算法1。

算法1K-SC 聚类算法

输入时间序列Ei，i＝1，2，…，N；簇个数K；初始簇中心μk，k＝1，2，…，K

重复

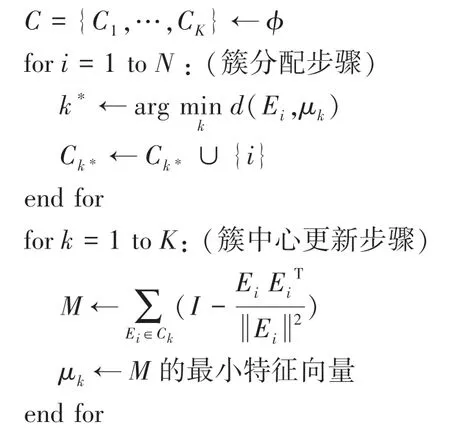
直到L不变

输出C，μ1，…，μK

2 实验分析

2.1 数据集

实验采用推特上2020 东京奥运会的数据，创建比赛事件的流量时间序列，并对事件进行聚类分析，找到同类事件的一般特性。 本文实验通过推特流媒体API 获取本届奥运会期间与场地自行车决赛项目相关的公开推文，对表1 中的8 项场地自行车比赛事件的流量时间序列进行聚类。 首先，获取各事件的初始主题标签，其中将“比赛名称”和“获胜者名字”视为最关键的主题标签；然后，获取各事件最终的主题标签，其中皮尔逊相关系数的阈值设定为0.8；最后，创建各事件的流量时间序列，将时间间隔t设置为5 min，并为各事件的时间序列选取合理且相同长度的时间区间。

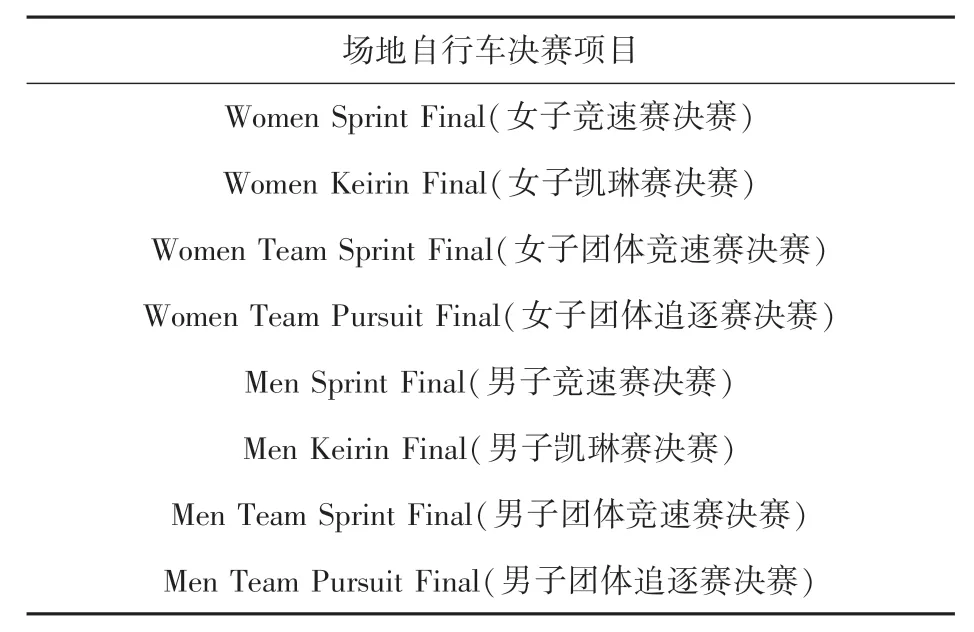
表1 本实验选取的场地自行车比赛名称Tab. 1 Names of the selected track cycling races in this experiment

2.2 确定簇的个数

对事件进行聚类前，首先需要确定簇的个数。本实验在不同的簇个数（即令K＝1，2，3，4，5，6）下执行K-SC 算法，得到目标函数值L（即距离平方和）收敛后的值，目标函数L的值随簇个数K的变化如图1 所示。 从图1 中可以看出，在K＝3 后，目标函数值的下降率变得平缓，簇个数对聚类目标值影响不大，因此将簇的个数设置为3。

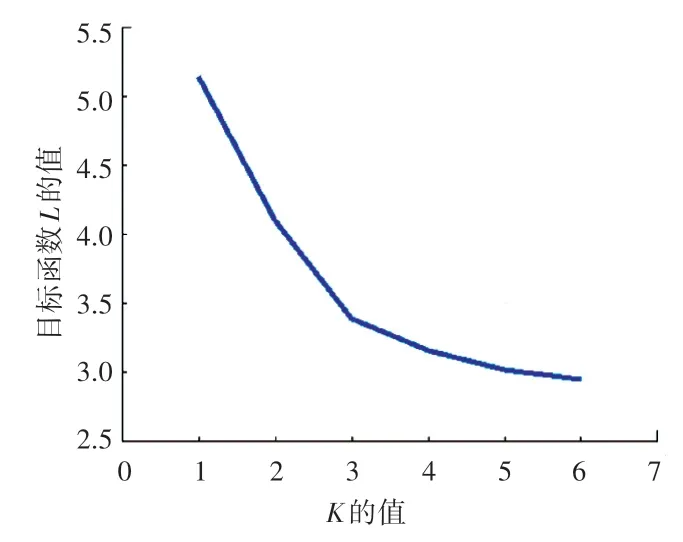
图1 目标函数L 的值随簇个数K 的变化Fig. 1 The change of the value of objective function L with respect to the number of clusters K

2.3 聚类结果分析

获取了场地自行车比赛事件的流量时间序列并确定了簇的个数后，用基于时间序列的K-SC 算法对事件进行聚类。 聚类结果见表2，可以看出这些比赛事件基本按照是否为团体项目被划分开；每个簇中每个事件的流量时序折线图如图2 所示，可以看出除了簇2 中事件的时间序列形状较为特殊之外，团体项目和个人项目显示出不同的时间序列形状。 簇1 中的团体项目事件都只有一个明显较高的峰值，而簇3 中的个人项目（男子或女子非团体项目）事件都显示出两个明显的峰值。 实验结果表明，聚类结果中同一类事件具有明显的共性特征，并且显示出类似的流量时序模式，从而验证了K-SC 算法对于基于流量时间序列的社交网络事件聚类的有效性。

图2 每个簇中比赛事件的流量时序折线图Fig. 2 Line graphs of the traffic time series for events within each cluster

表2 基于流量时间序列的场地自行车比赛事件聚类结果Tab. 2 Clustering results of track cycling events based on traffic time series

3 结束语

社交网络上用户实时生成的在线数据表现出丰富的时间动态性，但一些具有共性特征的事件可能会呈现出相似的流量模式。 本文根据事件的流量时间序列对事件进行聚类，找到事件的共性特征。 首先，利用皮尔逊相关系数来确定各事件的主题标签；然后，利用各事件的主题标签获得各事件的流量时间序列；最后，利用K-SC 聚类算法对多个事件的流量时间序列进行聚类，发现同类事件的共性特征。利用推特上2020 东京奥运会期间场地自行车比赛事件的推文数据验证了本文方法可以对基于流量时间序列的社交网络事件有效聚类，从而发现同类事件的共性特征。