基于线性回归和神经网络模型的二手车交易价格预测分析

郑爱萍， 李彬彬， 郭传好，2

（1 浙江理工大学经济管理学院， 杭州 310018； 2 浙江理工大学浙江省生态文明研究院， 杭州 310018）

0 引 言

中国汽车流通协会数据资料显示， 二手车市场的年交易量从2000 年的25 万辆增加到2021 年的1 769万辆，21 年间增长了约70 倍，市场发展和需求潜力巨大。 2022 年1 月21 日国家发展改革委等七个部门联合发布了“促进绿色消费实施方案”，该方案指出要积极发展二手车经销业务， 进一步扩大二手车流通。 二手车因其“一车一况”的特殊性，比一般的商品定价要复杂和困难，如品牌、 车系、 动力、行驶里程、 受损情况、 维修情况以及新车价格都会对二手车价格的制定带来影响，国家目前亦没有出台评判二手车资产价值的统一标准。 因此， 研究二手车的不同定价模型及价格预测方法，对于二手车市场价格的合理制定和二手车市场的健康发展具有重要的意义。

二手车定价方法的研究成果不多，且主要集中于传统的资产评估方法。 冯秀荣等［1］利用分析法得出影响二手车价值的重要因素是使用时间和里程；童佳等［2］指出二手车评估和传统资产评估的方法一样， 根据不同的评估目的、价值标准和业务条件可分为收益现值法、重置成本法和清算价格法；王传杏等［3］基于特征价值理论，利用多元线性回归建立了特征价格评估模型；程晓军［4］重置成本法中对成新率的权重系数，对二手车价格进行了更为全面的评估。

随着大数据和机器学习的快速发展，相关的数据分析和统计预测方法亦被越来越多的学者应用于经济管理问题的研究之中。 林建吾等［5］利用轻量化卷积神经网络对番茄病害进行图像识别；丁飞等［6］基于神经网络模型对房价进行预测；Pudaruth［7］研究了品牌、车型、 容积、 公里数等多个因素与价格的关系， 应用了包括k 近邻、 多元线性回归和决策树模型对毛里求斯的汽车价格进行预测；Gegic 等［8］建立了一个预测波斯尼亚和黑塞哥维那的二手车价格预测模型，分别使用了人工神经网络、支持向量机和随机森林3 种机器学习技术，该模型具有较好的预测效果，但模型的训练仅基于1 105个样本，模型的普适性有待提高；毛攀等［9］基于BP 神经网络建立了二手车价格评估模型，模型的可靠性与样本数量关系重大；郑婕［10］提出了基于随机森林和XGBoost（eXtreme Gradient Boosting）算法的二手车价格预测模型，但该模型是基于启发式算法，得到的定价解为局部最优而非全局最优；Arefin［11］采用决策树、支持向量机等机器学习方法对特斯拉二手车汽车进行研究， 结果表明增强决策树模型的预测效果最好；F Wang 等［12］使用Python中的自动特征处理工具与超参数优化方法对不同机器学习算法进行训练，发现使用极端学习树与随机森林算法训练的模型预测能力较好。

中国关于二手车交易价格预测的相关研究成果相对较少，存在模型特征量选择少、数据样本信息不足等问题。 本文深入分析探讨影响二手车交易价格的因素，建立二手车交易价格的多元线性回归预测模型和神经网络模型；为了改进模型的预测性能，同时利用自然对数对原数据进行数据处理，进而建立相应的预测模型。 为了评估不同模型的预测性能，基于58 同城二手车交易平台部分数据进行了相关的数值测试分析，结果表明经过自然对数处理数据集的神经网络模型具有较好的预测结果，对于二手车交易市场中价格的制定和预测以及二手车交易市场的健康发展具有重要的指导意义。

1 数据来源与分析

1.1 数据来源

本文利用的样本数据采集于2021 年58 同城二手车交易平台的30 000*36 的数据量，数据主要包括车辆基础信息、交易时间信息、 价格信息等，共计36 个特征变量，有15 个变量AF1-AF15 匿名变量，相关变量字段的信息见表1。

表1 数据集特征信息Tab. 1 Feature information of dataset

1.2 数据分析

为了便于对数据的理解和方便建模，本文对数据集的每个特征变量及数值含义进行简单的解释和说明，发现汽车的“展销时间”与交易价格之间没有显著的关系， 但“注册日期”和“上牌日期”与“二手车交易价格”之间有较明显的正向关系；在对“展销时间”和“注册日期”两列特征数据进行处理后，发现车辆的“使用时间”与“二手车交易价格”亦是直接相关的，与一般的交易情况亦是符合的，4 个特征变量与交易价格的关系图如图1 中所示。

图1 汽车上牌， 展销， 注册及其使用时间与二手交易价格的关系图Fig. 1 Diagram of relationship between licenseDate， tradeTime，registerdate， unsetime and price

本文使用的数据集中还包含15 列匿名特征，其中“匿名11”特征下的数据为字符型数据，无法准确判断其性质特征，为了减少不正确变量选择对模型效果的影响，故对“匿名11”特征及其数据进行删除处理。 “匿名12”是一组表示为长*宽*高的数据，将其理解为车辆外观尺寸的表达形式，车辆的大小与车长和轴距有关，且在未知轴距的情况下，可将车长作为区分车辆大小的重要指标。 为了数据处理和建模的方便，基于数据集本文将车辆区分指标划分见表2，同时将相关数据均转换为数值型数据。

表2 车辆大小指标与数据赋值Tab. 2 Vehicle size indicat or and data assignment

对数据缺失值进行检查分析，检查结果如图2所示，横坐标为其在整个数据集中所占的比例，纵坐标为含有缺失值的特征名称， 黑色部分表示该特征中所含缺失值的计数，本文以缺失值占比20%为分界线，即缺失值在整体数据中占比超过20%，则将该特征删除，否则使用该特征下数据的平均值对相关缺失值部分进行补充，即对缺失过多且会影响数据细节的缺失值进行剔除，对含缺失值较少的特征，在保证数据细节不受影响的前提下使用相关数据进行补充，如均值插补等，避免大量剔除缺失数据导致数据量不足。

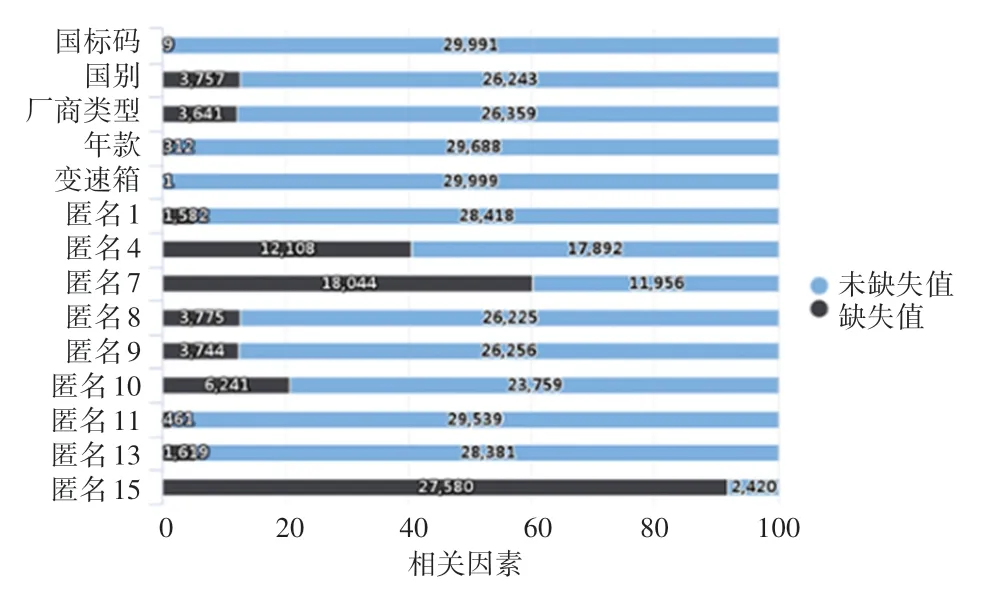
图2 含缺失值的特征及其缺失值占比Fig. 2 Features with missing values and the proportion of missing values

此外，本文使用箱形图分析数据集的离散情况，并判断数据集中是否存在离群点（异常值）。 异常值的处理以“二手车交易价格”为重点特征， 即在“二手车交易价格”这一特征中存在异常值。 为了提高所建立模型的普适性，在对异常值处理时本文允许存在离群程度不大的异常值，但对极端异常值所在行进行剔除， 相关结果如图3 中所示。

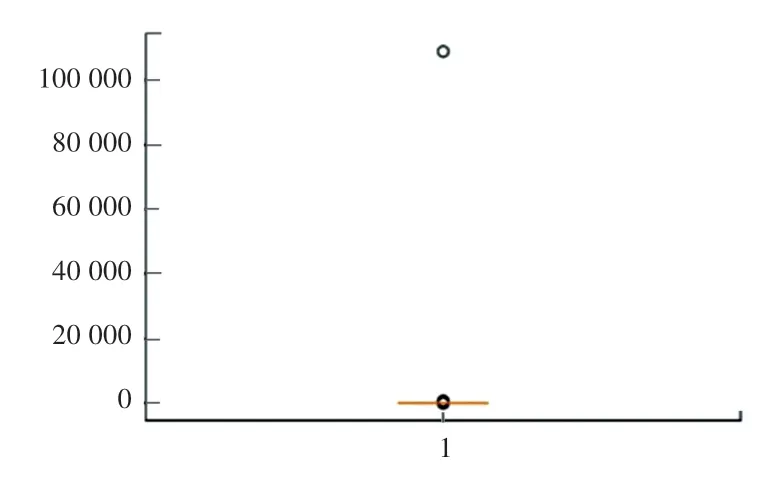
图3 二手车交易价格箱形图Fig. 3 Box plot of transaction price

二手车交易价格分布直方图和自然对数处理后分布直方图如图4 所示。 由图4（a）可知，此时二手车交易价格数据分布呈现一个近似正偏的正态分布；如图4（b）所示，为了降低数据分布不规范对建立模型结果的影响， 利用自然对数对二手车交易价格数据进行变换处理，进而可得到一个数据分布较规范的二手车交易价格数据集。

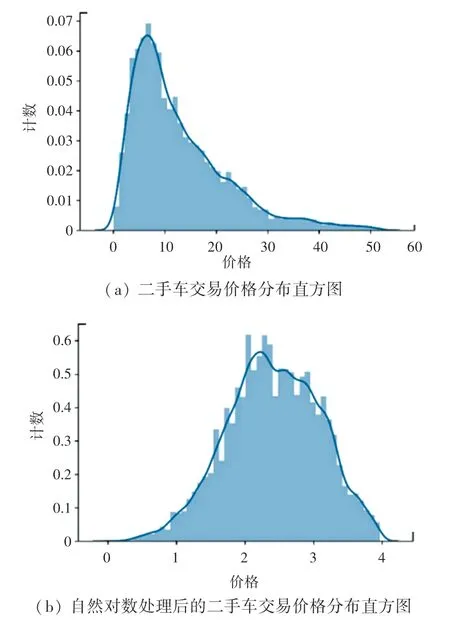
图4 二手车交易价格分布直方图和自然对数处理后分布直方图Fig. 4 Histogram of transaction price and its nature longarithm

对初始数据集预处理，最终得到一个29319*28 的数据集，其中对该数据集的描述性统计分析结果见表3。

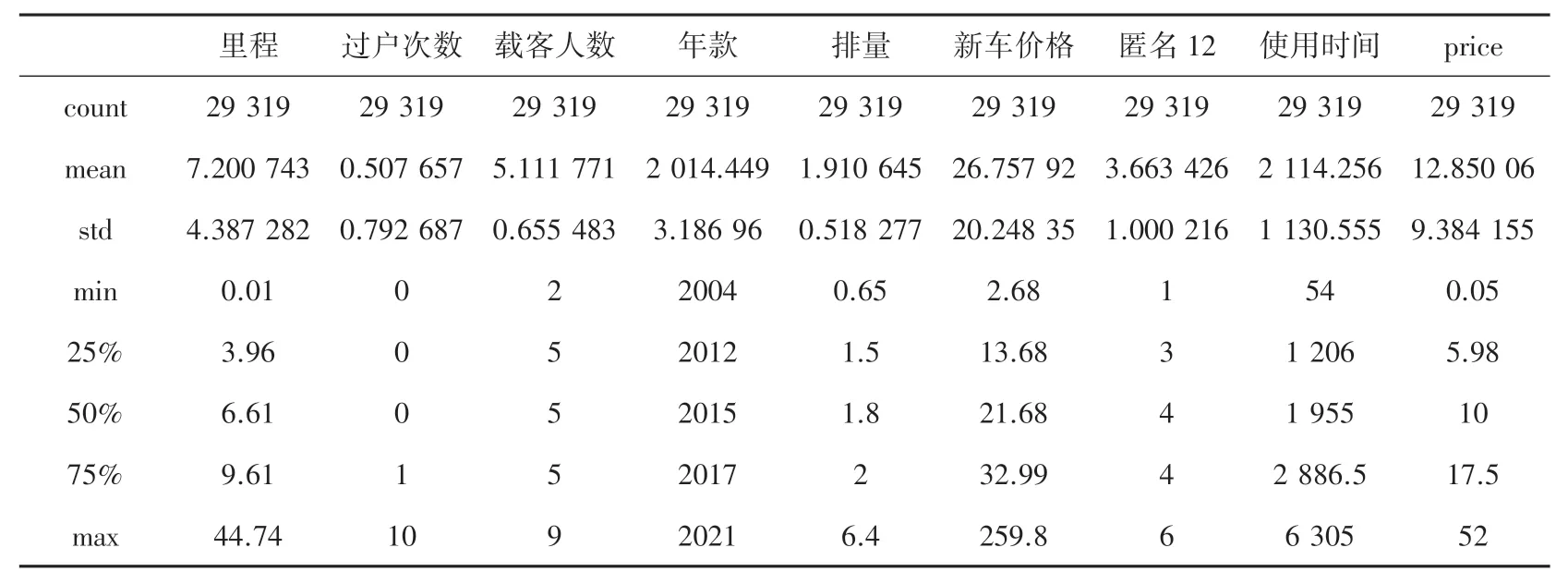
表3 二手车交易数据的描述性统计结果Tab. 3 Descriptive statistics of transaction dataset

首先，在数据集中一部分特征的数据属于分类赋值的离散数据，但无法得知其确切的含义，如假设“品牌”与“二手车交易价格”是正相关的， 可以得出：当“品牌”的数值越大时，“二手车交易价格”也就越大，但由于不知道特征“品牌”数值的具体含义，没办法对这组关系进行更深入的分析，故而在模型的建立与求解中虽仍将这部分特征引入模型，但不再分析其结果的具体意义；其次， 本文视里程和使用时间为汽车的使用程度，其他几个特征视为汽车自身的情况， 在汽车使用程度中平均行驶里程为7.20 个单位，最大行驶里程为44.74 个单位，即大部分车辆的使用程度都较低，其平均使用时间为2 114.26 天，结合平均行驶里程可知，展销的二手车具有里程短，使用时间长等特点，符合二手车的商品特征；再次， 平均过户次数为0.51 次，且至少50%的车辆都未经过过户，说明在这些展销的二手车中大部分都是新车购车车主将该车辆作为二手车转售的，平均载客人数和平均车辆大小均说明展销的二手车主体是更经济适用的中等大小、可载客5 人的车辆；最后，平均新车价格为26.76万元，但平均二手车成交价格为12.85 万元，跌幅明显，即汽车作为不保值商品，在二次售卖时价格会有较大幅度的下降，从新车价格分布中可以看出， 大部分展销出售的二手车在一开始购买时75%的汽车新车售价为35 万以下，即二手车交易市场的流通主体是售价偏大众的经济型汽车。

2 建模与分析

为了建立二手车价格的预测模型，本文先对数据集中的28 个特征进行了相关性分析，并给出相关系数热力图，如表4 和图5 中所示。 表4 给出了与二手车交易价格呈现相关性最大的前8 个特征变量及其相关系数大小， 可知新车价格对二手车交易价格的影响最为显著，相关影响系数为0.810 1；其它对二手车交易价格影响较大的特征是排量、匿名12、 匿名2、匿名8、年款、厂商类型及使用时间，其中使用时间对二手车交易价格的影响呈现负相关性。 图5 中各个特征变量标签的释义见表1，越靠近蓝色代表正相关性越强，越靠近红色则代表负相关性越强，即颜色越深的区域的相关系数的绝对值越接近1， 此时两个特征变量越相关。

图5 特征相关系数热力图Fig. 5 Heat map of correlation coefficient

表4 二手车交易价格与部分特征的相关系数Tab. 4 Correlation coefficient between transaction price and some characteristic variables

2.1 多元线性回归模型

基于特征变量的相关性分析结果，以“二手车交易价格”为因变量，建立多元线性回归预测模型。在0.1 显著性水平下，对模型检验分析发现：“里程”、“过户次数”和“使用时间”3 个特征变量与“二手车交易价格”呈现负相关性，而且这些特征变量也可作为车辆使用程度的描述，即车辆使用的程度越高，该车辆作为二手车售卖时成交的价格就越低。同时，“二手车交易价格”同“载客人数”、“排量”、“新车价格”和“匿名12”呈现显著正相关性。 为了保证模型的显著性效果，筛去与“二手车交易价格”相关性较低的特征变量，最终得到二手车交易价格预测回归模型如式（1）：

其中，特征变量的含义见表1。

利用自然对数变换处理过的特征变量数据集具有较好的分布特征和度量性质，因此利用自然对数对所有特征变量数据进行处理，并对处理后的数据进行多元线性回归建模，对数变换函数如式（2）：

其中，Xi为特征变量，即表1 中所示的变量；ε为回归的误差；βi是回归方程系数；Y为二手车价格。

同理， 在相同显著性水平下，可得此时回归预测模型如式（3）：

其中，特征变量的含义见表1。

2.2 模型结果分析

为了有效的评价和对比分析所建预测模型的有效性和准确性，本文采用平均相对误差（MAPE， Mean Absolute Percentage Error）和准确率（Accuracy5） 的线性组合作为模型的最终评价指标M，式（4）：

MAPE又称相对误差（APE，Absolute Percentage Error）的算术平均值。 为了降低单次预测中噪声数据对预测结果准确性的影响，通常用于评估预测模型预测结果的可靠性和精度，式（5）和式（6）：

其中，为二手车价格的预测值；y为相应二手车价格真实值；m是价格预测实验的次数（本文m＝29 319）。

准确率（Accuracy5） 通常表示模型预测正确的样本在实验总样本中所占比例， 式（7）：

其中，0.05 表示相对误差比例，APE≤0.05 表示相对误差小于5%，即预测值相对于真实值的误差比例不超过0.05，故而Accuracy5又称为5%误差准确率。

基于数据预处理所得到的数据集，利用多元线性回归预测模型和多元线性回归（自然对数）预测模型分别对二手车交易价格进行预测分析，对比结果见表5。 每一次价格预测实验都会对应产生一个APE值， 一共进行了29 319次价格预测实验。 由表5 中结果可知， 基于自然对数处理过的数据集而建立的预测模型，其准确率和平均相对误差都要优于基于原数据集而建立的预测模型，模型的整体性能提升了1 倍多。

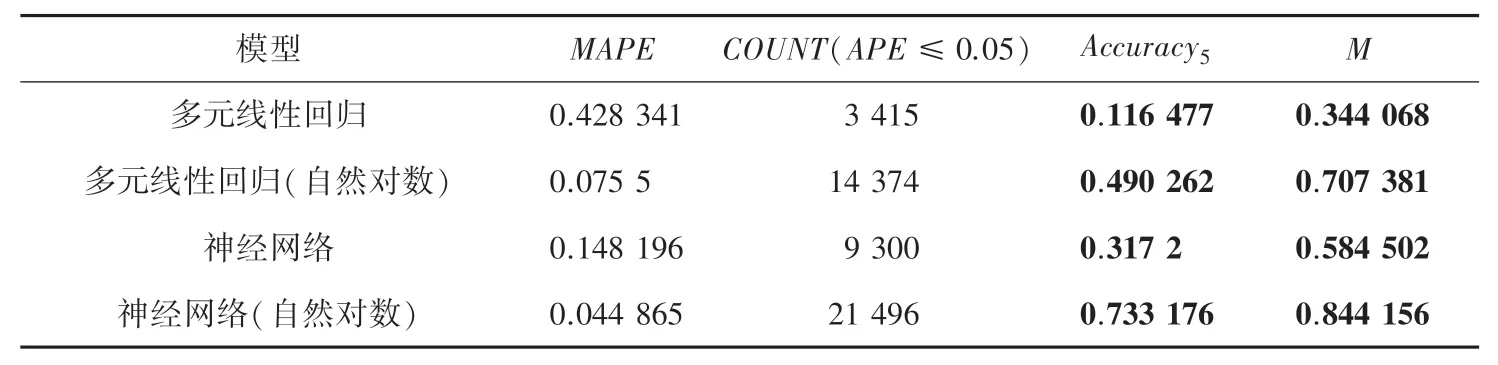
表5 不同模型评估对比结果Tab. 5 Comparison results between different models

为了进一步对比分析本文所建回归预测模型的性能，利用MATLAB 软件工具箱中集成的神经网络模型，设计并建立了一个基于监督学习的神经网络模型，其中训练集、测试集和检验集的比例分别是60%，20%和20%，隐藏层神经元取27 个，同时选择库函数trainlm 作为训练函数， 并使用MATLAB 自带的Levenberg-Marquardt 算法求解生成的神经网络模型。

基于数据预处理得到的数据集，利用MATLAB中集成的神经网络建模工具，得到了一个基于神经网络模型的二手车交易价格预测模型，模型的拟合误差效果如图6 所示。 由图6 可知，最佳拟合结果出现在第72 次迭代，此时验证集误差为3.507 4。神经网络不同训练集拟合结果如图7 所示， 图7（a）中蓝线代表神经网络训练出的拟合模型，黑色气泡点代表训练集输入的数据，气泡点越靠近蓝线则代表训练结果越好，可见大部分气泡点都围绕在拟合线附近，仅存在少部分孤立点，由此可知该模型训练集的拟合程度较好；图7（b）图中数据占总数据集的20%，绿线表示其拟合模型，可见虽然黑色气泡点存在部分孤立点，但数据整体基本都在拟合线附近；图7（c）中有较多的气泡点偏离红色拟合线较多；图7（d）中数据集综合拟合程度较高，网络训练整体效果较好。

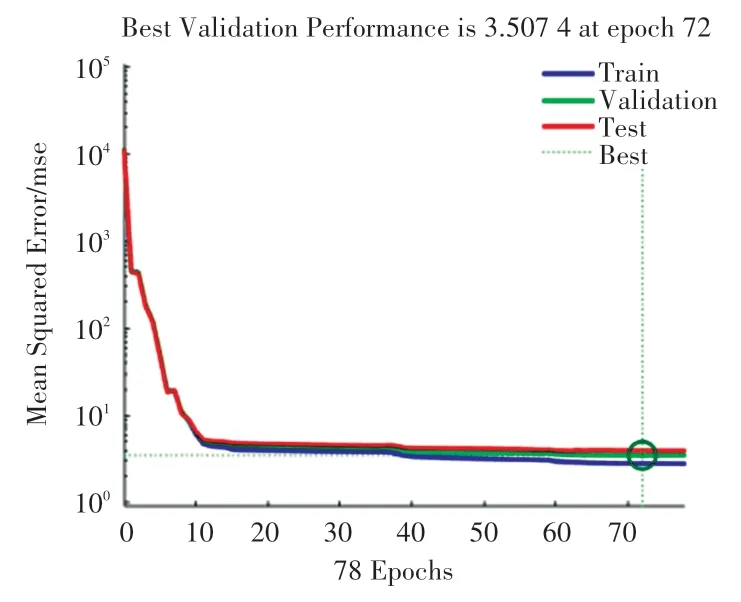
图6 神经网络拟合误差Fig. 6 Fitting errors of neural network

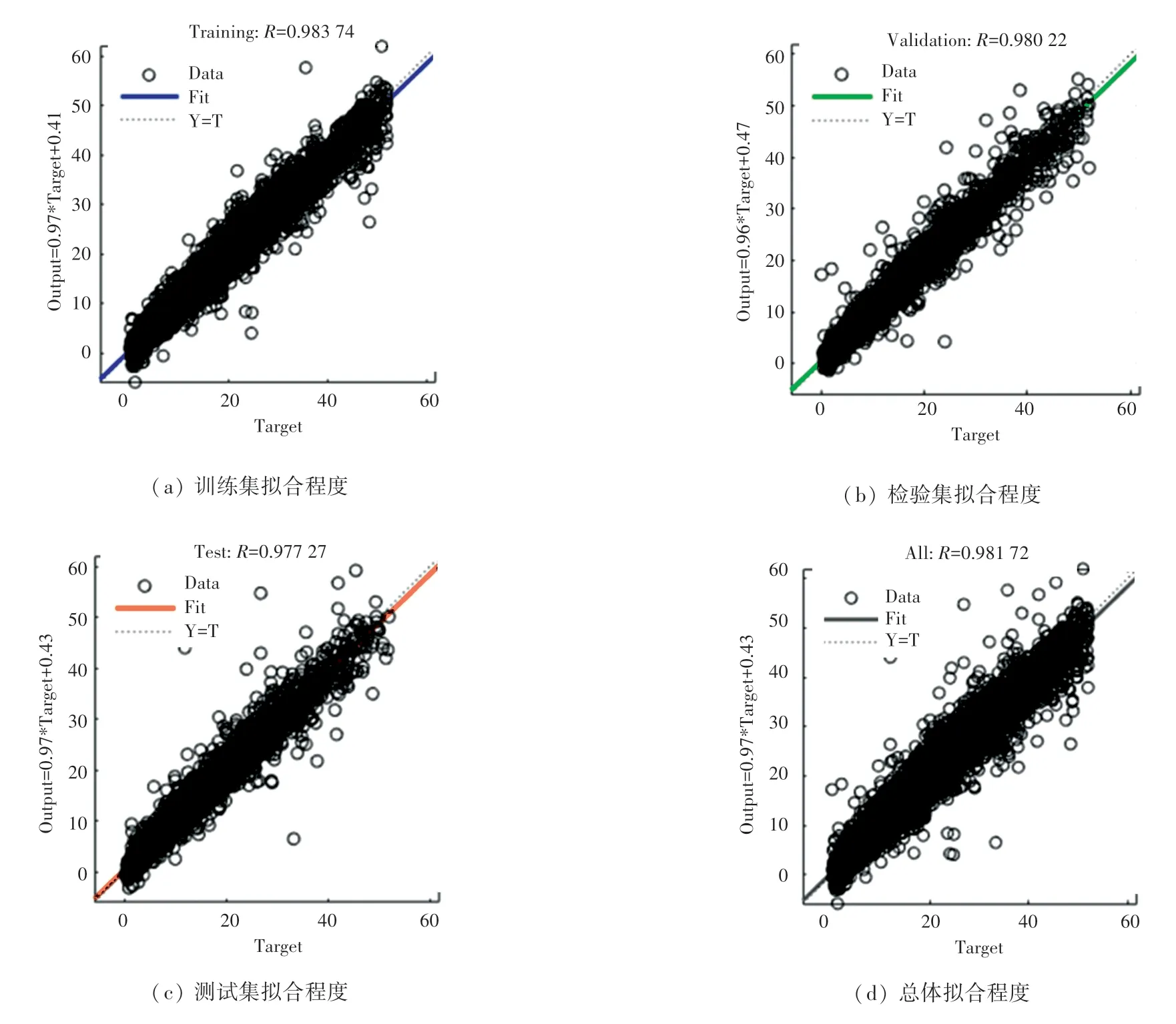
图7 神经网络不同训练集拟合结果Fig. 7 Fitting degree of different training sets for neural netwok

基于自然对数处理后的数据集而建立的回归模型具有更好的预测效果，因此在神经网络模型中利用自然对数对原数据集进行相关变换和处理，得到了基于神经网络经自然对数处理后的二手车交易价格预测模型，该模型的相关拟合结果如图8 和图9中所示。 由图8 可知迭代仅需要55 次便达到最优，较数据优化前模型计算成本有一定程度的降低，验证集误差仅为0.014 701，较优化前模型误差降低了300 多倍，模型的准确性有了极大的改进。

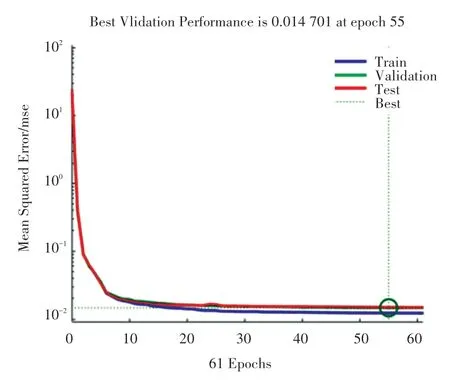
图8 基于自然对数的神经网络拟合误差Fig. 8 Fitting error of neural network based on natural logarithm

图9 基于自然对数的神经网络不同训练集拟合结果Fig. 9 Fitting degree of different training sets for neural network based on natual logarithm

神经网络预测模型和神经网络（自然对数）预测模型的性能结果也与多元线性回归预测模型和多元线性回归（自然对数）预测模型的相关结果进行了对比分析，相关对比结果见表5。 由表5 可知，基于对数的多元线性回归（自然对数）模型的效果要优于神经网络模型， 其MAPE是神经网络的一半，且Accuracy5有20%的提升。 数据的相关结果亦表明，基于自然对数处理过的数据而建立的模型具有较好的预测性能。

3 结束语

二手车交易价格的预测与制定对二手车交易市场的良序发展具有重要的指导作用。 本文基于2021 年58 同城二手车交易平台中的部分脱敏数据集，分别建立了多元线性回归和神经网络二手车交易价格预测模型，数值测试的结果表明基于神经网络建立的预测模型相比于基于多元线性回归建立的预测模型，准确性和精确性整体提高了近1 倍，同时在对数据进行自然对数归一化处理后的预测模型，平均相对误差降为原模型的1／5，精确度提升为原模型的2-3 倍，即利用经过自然对数归一化处理的数据集，基于神经网络建立的价格预测模型具有更好的拟合和预测效果。 相关研究成果对于探讨二手车市场中的不同定价模型及其优缺点，指导二手车交易价格的合理制定和预测以及二手车交易市场的健康发展具有重要的现实意义。