基于k-means 特征的适应性近似最近邻搜索算法

2023-09-21胡文洁杨凯祥谭宗元

智能计算机与应用 2023年9期

胡文洁，杨凯祥，谭宗元

（东华大学计算机科学与技术学院，上海 201620）

0 引言

随着互联网技术的快速发展，文字、图片和视频等信息呈指数式增长，给信息检索带来了巨大的挑战。最近邻检索问题最早采用暴力搜索的方式，而暴力搜索通常采用线性扫描的方式，即计算目标点与每个数据点的相似性，从而返回与目标点最相似的结果。针对十亿规模的高维数据，线性扫描效率过于低下的问题，研究者们开始研究海量数据中近似最近邻搜索问题，力求在数据集庞大的条件下，返回与目标最相似的K个邻居。近似最近邻搜索在信息检索、人脸识别、文件检索、推荐系统等方面发挥着重要作用。

面对大规模的高维数据，近似最近邻搜索算法主要解决两个问题：降低内存占用和加快搜索时间。在降低内存占用方面，近似最近邻采用量化技术，将原始数据压缩为二进制编码进行存储，很大程度上降低了内存开销，其代表性算法包括乘积量化算法［1］、优化的乘积量化算法［2］和加和量化算法［3］。在加快搜索时间方面，近似最近邻搜索领域最常采用的解决措施是对数据构建索引，使用不同的方法对数据进行划分，在查找目标数据的最近邻时，仅仅搜索与目标数据最接近的一类数据，减少了数据的比对个数，降低了查询时间。其中，基于向量量化的近似最近邻搜索算法［1-4］，根据数据构建倒排索引；而基于近邻图的近似最近邻搜索算法，是对数据构建图索引［5-6］。

目前，在根据索引搜索目标数据的最近邻算法中，通常只搜索固定的粗聚类或者固定的数据点，这会导致搜索访问不必要的数据点。因此，本文在IVF-HNSW 算法的基础上，结合数据的k-means 特征，动态预测每个查询点需要搜索的粗聚类中心的个数，降低了查找次数以及查询点平均的搜索时间。

1 相关工作

1.1 相关定义

最近邻搜索将若干个数据点与给定目标进行匹配，并返回距离目标最近的数据点。当计算目标向量和数据集向量间的距离时，常用的指标包括余弦相似度、汉明距离和欧式距离。其中，欧式距离使用向量间的绝对距离表示两者的远近程度。本文研究中，采用欧式距离计算向量间的距离。欧式距离定义为：在n维空间中，给定数据集中任意一条向量x＝（x1，x2，…，xn）和目标向量y＝（y1，y2，…，yn），向量x和向量y间的距离计算如式（1）：

欧式距离的值越小，表示两向量越近；反之，说明两向量距离越远。

最近邻搜索针对目标数据返回精确的搜索结果。但是当数据量增加到百万甚至十亿规模并且维度上升到成百上千，精确的最近邻查找的代价非常高，于是在搜索时，牺牲可接受搜索精度范围内提高搜索的准确率，返回与目标数据最相似的K个最近邻，即近似最近邻搜索。近似最近邻搜索可定义为：

在D维空间中，给定包含N条向量的数据集合B＝｛b1，b2，…，bn｝和目标数据t，并确定返回最近邻的个数（K值），则近似最近邻搜索根据距离函数d（t，b），返回目标数据t在数据集合B中的K个最近邻，即：

适应性搜索指给定一个查询点，利用数据点的k-means 特征和回归模型，预测其终止条件为τ，则此查询点仅搜索τ个粗聚中心或者τ个候选节点。

1.2 近似最近邻搜索

目前主流的近似最近邻搜索方法包括基于哈希的近似最近邻快速查找技术、基于树的最近邻搜索方法、基于向量量化的最近邻搜索和基于图的最近邻搜索等。

基于树的搜索方法以KD-树［7］为代表。 KD-树首先会选取数据各维度中方差最大的维度p；其次以维度p为基准对数据排序，选取位于中位数的数据点b；最后将数据点b作为阈值，则全部数据点被分为两部分。将数据点b作为根节点，两部分数据分别作为其左右子树，并递归将其左右子树展开，最终将全部数据构建为一颗索引树。在查询目标数据的最近邻时，根据二分搜索，查找左子树或右子树，直到搜索到叶子节点，返回目标数据的最近邻。

基于哈希的近似最近邻查找算法中，局部敏感哈希（LSH）［8］占据重要地位，其主要思想是利用哈希函数簇，将原始数据映射到低维空间，经过哈希函数簇之后，原始空间中相似的两条数据以更大的概率被分配在同一个桶中；反之，不相似的两条数据被分配在不同的桶中，并建立桶编号和数据点的索引关系。在查找目标数据的最近邻时，利用哈希函数簇对目标数据进行哈希，并计算目标数据和其对应的桶中的全部数据的距离，返回最近邻。

基于向量量化的方法，以乘积量化（PQ）［1］为代表。乘积量化的思想是对高维数据进行正交分解，将高维特征空间划分为M个低维子空间，在每一个低维子空间中运用k-means 方法对所有的数据进行聚类，并对聚类中心进行编码，每个数据用其对应聚类中心的编码表示。在查询过程中，使用ADC 方法计算目标向量与数据库向量间的距离，并利用lookups 表存储查询向量的每一段子向量到各编码的距离，通过lookups 表查询M段距离并进行加和，最终将距离排序，返回目标向量的最近邻。

在十亿规模的数据集上，原有的ADC 方式虽然加快了查询时间，但仍然是线性扫描，耗时较多，因此Jegou 等人提出结合倒排索引系统［4］进行搜索。倒排索引首先使用k-means 方法对所有的数据进行粗聚类，并计算每个数据的残差，即原始数据和对应粗聚类中心的差值，之后再使用乘积量化算法对所有残差进行量化。最终每一类建立一个倒排列表，倒排列表中存储该类中所有数据的id 和PQ 量化的结果。在查询向量搜索最近邻的过程中与所有的粗聚类中心计算距离，并选取w个距离最近的粗聚类中心，从w个类中包含的所有数据点中选取最近邻。

基于图的方法，代表性的方法为分层可导航小世界（HNSW）［7］，其做法如下：在构建图索引的过程中，当插入一个新数据点时，计算新数据点插入的层数l，将其插入到0-l层，并在每一层选取新数据点的m个最近邻并连接，直到数据集中的数据点全部插入图索引，则多层索引构建完成。查询向量搜索最近邻时，从最上层的入口点开始，计算其在当前层最近的邻居，并将其作为下层搜索的起始点。当搜索到最底层时，构建长度为w的优先队列，用于存储候选节点。查询向量在优先队列中进行精确的查找，返回其最近邻。

1.3 IVF-HNSW 算法

IVF-HNSW 算法针对十亿规模数据集，结合倒排索引和图索引，实现了更细粒度的划分。一方面，IVF-HNSW 算法将聚类得到的区域划分为更小的区域；另一方面，在查找最近邻时，利用剪枝策略过滤部分数据点，加快了检索速度。具体实现过程如下：

在构建倒排索引的过程中，首先将整个空间划分为若干个区域，并计算每个区域的粗聚类中心（质心）。在每个区域中再次进行划分，与普通的划分方式不同的是，IVF-HNSW 算法采用凸组合的形式表示子质心，即每个区域的子质心由质心和此质心相邻的L个最近质心的凸组合表示。凸组合形式的优势在于不需要存储码本，节省了内存空间的占用。其次每条数据库向量被量化到最近的子质心后，计算其残差，即原始向量和其对应子质心的差值，并利用乘积量化算法对残差进行编码。最后建立倒排索引，键为质心，值为质心对应区域中包含的数据点，并且同一个子区域中的数据排列在一起。

在查询向量搜索最近邻的过程中，数据集的规模导致查询向量搜索质心的效率低下，因此IVFHNSW 算法选择对质心构建HNSW 索引，用于快速查找最近的质心。搜索到最近的质心S后，查询向量和质心S中包含的子质心计算距离，并计算距离的均值E，当查询向量和子质心的距离大于距离E时，则跳过对应的子区域，过滤不可能成为最近邻的数据点；当查询向量和子质心的距离小于或等于距离E时，则在对应的子区域中进行搜索，即计算查询向量的残差，并利用ADC 的方式计算查询向量和已压缩向量的距离，将距离排序，最终返回查询向量的最近邻。

2 自适应的提前终止查询算法

本文通过分析固定的终止条件对近似最近邻搜索算法产生的影响，在查询阶段将原始的IVFHNSW 算法和基于k-means 特征的提前终止算法相结合，使得每个查询点进行适应性搜索，优化了查询过程，并在sift 和deep 数据集上通过实验进行证明。

2.1 问题分析

基于倒排索引结构的近似最近邻搜索算法（如IVFADC 算法等），通常使用固定的搜索终止条件（如Nprobe），Nprobe 指每个查询点所需要搜索的粗聚类中心的数量。基于图索引的搜索算法（如HNSW 算法），通常也使用固定的搜索终止条件（如Efsearch）。 Efsearch 参数指图索引的0 层使用长度为efsearch 的优先队列，用于存储候选节点，每个查询点在优先队列中进行精确的搜索。因此终止条件（即nprobe 和efsearch）的设置，是影响搜索准确度的关键指标。随着终止条件的增大，查询点需要搜索数据点的个数增多，则搜索准确度越高，花费的搜索时间也越长；反之，虽然搜索时间较少，但搜索准确度会逐渐降低。

在实际搜索过程中，存在每个查询点终止条件不同的情况，即有些查询点只需要很小的终止条件α1就可以检索到最近邻，而一些查询点需要更大的终止条件α2才能搜索到最近邻，其中α2＞α1。对于这种情况，为了满足搜索精度的要求，终止条件的设置需要保证绝大部分查询点搜索到最近邻，即终止条件大于α2。由于所有的查询点使用相同的终止条件，则导致“容易”搜索到最近邻的查询点花费时间搜索不必要的数据点，造成了平均搜索时间升高的问题。

由于IVF-HNSW 算法在查询阶段使用固定的终止条件进行搜索，因此本文采用k-means 特征，动态预测每个查询点的终止条件，并使得每个查询点在对应的终止条件下停止搜索，实现了适应性搜索，降低了平均查询时间。

2.2 算法实现

本文在IVF-HNSW 算法上的优化包括以下步骤：收集数据集的特征、训练模型、预测查询点的停止条件、建立IVF-HNSW 索引并整合模型。

2.2.1 收集数据集的特征

数据集特征包括训练集的输入特征和输出特征两部分。输入特征表示训练集中每个数据点的kmeans 特征，输出特征指训练集中每个数据点在IVF-HNSW 算法中真实的停止条件。收集k-means特征首先利用k-means 方法，将训练集聚到一万个类聚类中心，计算每个数据点最近的50 个聚类中心。选取特征见表1。

其中，t表示训练集中任一数据点，dist（t，ith nearest coarse cluster centroid）表示数据点和其第i个聚类中心的距离，因此选取的特征共10 个，包括数据点到其第5、10、15 等聚类中心与数据点到最近的聚类中心的距离的比值。

收集输出特征是在查找过程中，判断每个数据点是否搜索到其真实最近邻，如果搜索到真实最近邻，则记录搜索的倒排列表的个数。由于数据库向量中存在重复的向量，因此每个数据点可能会有多个距离相同的真实最近邻，于是在收集输出特征的过程中，只要数据点搜索到其真实最近邻中的一个，则认为此数据点搜索到真实最近邻并记录下最小访问点的个数。

2.2.2 训练模型

将每个数据点的k-means 特征作为输入，对应的真实停止条件作为输出，选择神经网络模型对数据进行回归拟合。神经网络回归模型的输入层为数据的10 个k-means 特征；隐藏层的个数为2，其神经元个数设置为100；输出层个数为1，即神经网络预测的数据点的终止条件。当训练次数为50 次时，模型训练完成。

2.2.3 预测查询点的停止条件

首先收集查询集中每个查询点的k-means 特征，计算每个查询点的110 个聚类中心，选取查询点到其最近的聚类中心的距离和查询点到其第5、10、15 等聚类中心的距离的比值，作为10 个k-means特征。查询点的k-means 特征作为神经网络回归模型的输入，预测其终止条件，即需要搜索的倒排列表的个数和候选节点的个数。

2.2.4 建立IVF-HNSW 索引并进行适应性搜索

将训练集聚类到一百万个粗聚类中心后，建立相应的倒排索引并根据粗聚类中心建立HNSW 索引。在IVF-HNSW 索引的基础上，加载每个查询点的停止条件，并将nprobe 和efsearch 参数设置为对应的终止条件，保证每个查询点进行适应性搜索。

3 实验

本文采用sift1B、deep1B 以及spacev1B 3 个公开的数据集。每个数据集包括3 部分：数据集、训练集和查询集。训练集用于训练回归模型，数据集和查询集用于评估最近邻搜索的准确度。 spacev1B 数据集包含的训练集是从数据库集中切分的一千万条向量，所以数据库集仅包含九亿九千万条向量。有关数据集的详情见表2。

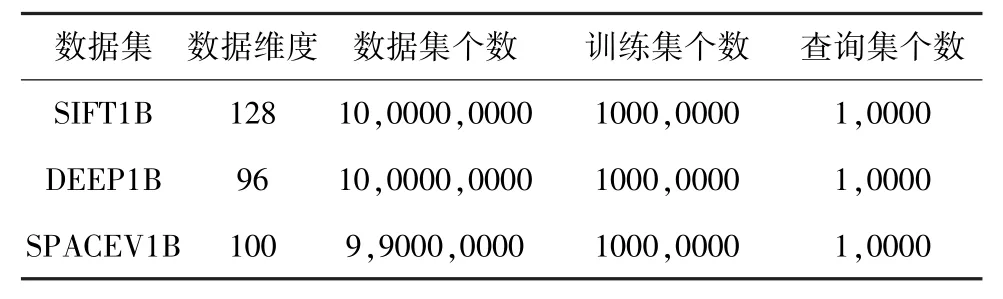
表2 数据集Tab. 2 Datasets

SIFT 数据集是从图像中提取的局部特征描述符，每张图片的描述符组成128 维的特征向量，其中每个坐标为0 ～128 的整数；DEEP 数据集是由自然图像经过CNN 后生成的96 维特征向量，其中每个坐标的取值范围为-1 ～1 的浮点数；SPACEV 数据集是微软必应最先发布的数据集，由Microsoft SpaceV 模型生成的数据库向量和查询向量，其中每条向量的维度为100 维，每个坐标的取值范围为-128～128 的整数。

本文采用召回率recall1＠100 衡量搜索最近邻的准确度，即搜索结果的第1 最近邻在其前100 个真实最近邻中的查询点个数占所有查询点个数的比例。召回率越高，表示搜索的准确度越高。在比较原始的IVF-HNSW 算法和本文优化的算法时，采用控制变量法，即达到相同的召回率时，对比两种算法的平均查询时间。在相同的召回率下，平均查询时间越短，证明算法的性能越好。

原始的IVF-HNSW 算法和本文优化的自适应搜索算法在sift1B、deep1B 和spacev1B 3 个数据集上得到的实验结果如图1 ～图3 所示。其中纵轴表示算法达到的召回率recall1＠100，横轴表示在对应的召回率下，算法对于所有查询点的平均查询时间（以ms 为单位）。蓝色的实线表示基准的IVFHNSW 算法，红色的实线表示基于IVF-HNSW 算法的自适应搜索算法。

图1 平均查询时间-召回率（SIFT1B）Fig. 1 Average query time-Recall （SIFT1B）

图2 平均查询时间-召回率（DEEP1B）Fig. 2 Average query time-Recall （DEEP1B）

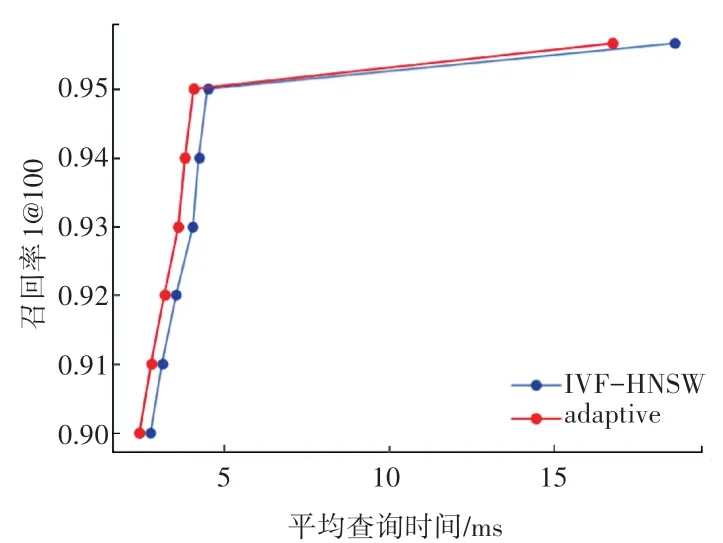
图3 平均查询时间-召回率（SPACEV1B）Fig. 3 Average query time-Recall （SPACEV1B）

从中可以看出，自适应搜索算法在低召回率和高召回率下的平均查询时间均低于IVF-HNSW 算法，并且随着召回率的升高，减少的查询时间越多。在SIFT1B 数据集上，当两种算法的搜索准确度都达到最高召回率0.958 6 时，IVF-HNSW 算法的平均查询时间为6.03 ms，而自适应搜索算法的平均查询时间为5.15 ms，在原始算法的基础上降低了14.6%；当两种算法的召回率为0.95 时，基准算法的平均查询时间为3.78 ms，而自适应搜索算法的平均查询时间为2.52 ms，下降了33%。结果表明，在SIFT 数据集上，高召回率下的时间下降更多。

然而在DEEP1B 数据集上，两种算法达到最高召回率0.948 9 时，IVF-HNSW 算法的平均查询时间为5.13 ms，而自适应优化算法的平均查询时间为3.75 ms，降低了27%；在召回率0.90 下，IVF-HNSW算法的平均查询时间为1.94 ms；而自适应优化算法的平均查询时间为1.52 ms，降低了21%。说明随着召回率的升高，平均查询时间在原始IVF-HNSW 算法的基础上下降的幅度更大。

对于SPACEV1B 数据集，在低召回率下两者没有区别，但是在最高召回率0.956 6的情况下，平均查询时间从17.42 ms 降低到15.25 ms，降低了12.5%，说明自适应算法在高召回率下具有更高的优势。

从实验结果分析可以看出，本文优化后的自适应搜索算法的性能全面高于原始的IVF-HNSW 算法，在相同的召回率下，进一步降低了平均查询时间。由于不同数据集生成特征向量的方式不同，所以同一种算法在不同的数据集上表现不同。在sift数据集上，自适应搜索算法在低召回率上更有优势；在deep 数据集的高召回率下，查询时间下降的百分比更多；在spacev 数据集上，自适应算法在低召回率下的表现几乎和原始的IVF-HNSW 算法重合，但是在高召回率下的查询时间有很大程度的降低。