鞋底喷胶轨迹自动生成算法研究

周栋锋， 李俊峰

（浙江理工大学信息科学与工程学院， 杭州 310018）

0 引 言

目前，国内外的鞋底喷胶系统都向智能化、自动化、可视化的多功能数控集成系统的方向发展，但很多鞋业的片底涂胶还采用人工的方式。 机器视觉可以代替人眼对目标进行检测和分析，并做出相应的处理，现在的视觉喷胶技术大都集中在高帮鞋型，通过3D 点云的方式提取点［1］。 对点云进行处理不仅十分费时，且对片底来说，采用线激光或结构光提取轮廓精度不会很高。

在边缘提取算法上，郭琳琴等［2］提出了基于分数阶微分算子的图像边缘检测方法，通过构造微分算子去计算x方向与y方向上的分数阶算子，此方法的计算复杂度比较高，且只计算了两个方向的梯度，在边缘准确性上不太高；Feng Lin 等［3］提出了基于模糊径向基数神经网络的图像边缘检测算法，黄胜等［4］提出了基于语义信息的精细化边缘检测方法，郑恩壮等［5］提出了各向异性的多尺度边缘检测算法，这3 种方法均需要对目标图片进行人工标注边缘，对于工业生产来说既费时又不能保证稳定性；田贝乐等［6］提出一种改进的小波变换法替代高斯滤波，实现对图像的降噪，采用改进的迭代算法对高低阈值进行计算，虽然增加了鲁棒性，但边缘的细化程度并不是很高；Hao［7］在普通Sobel 算法基础上增加了其它方向上的梯度检测，但这种只增加边缘检测，不做边缘细化会产生边缘断开的情况；Orhei Ciprian 等［8］在图像滤波上采用扩张滤波器，对边缘会有比较好的保留效果，但对于背景复杂度不高的图片来说会增加边缘的宽度，导致精度有所下降；G.Domínguez-Rodríguez 等［9］提出了新的边缘细化方法，计算x、y方向上的梯度并通过循环方式与原图进行卷积，将卷积结果与设定阈值进行比较，在保留边缘的情况下细化边缘，整个处理过程中不仅要保证边缘提取的准确性，还要保证处理速度不能过慢。

完成边缘提取后，对边缘进行进一步处理得到喷胶轨迹点，再通过标定的方式将图像坐标转变为机械坐标。 在标定上，Kenji Koide 等［10］都提出了手眼标定的方式，这些手眼标定的方式需要计算许多的转换矩阵，计算复杂度比较高，且多次转换计算有可能导致最终的误差偏大。

为解决3D 相机成本过高且边缘检测精度不高的问题，本文提出采用2D 相机采集图像并使用改进Sobel 算法提取片底边缘轮廓的方式来代替3D相机进行边缘提取。 为解决普通九点标定算法引入过多转换矩阵导致转换误差过大问题，本文提出新的标定方式，直接对图像坐标与机器人世界坐标系进行转换，通过将得到的图像坐标系的坐标数据与转换矩阵相乘来得到世界坐标系实际数据。

本文首先使用自动掩膜生成算法去除背景干扰，再通过改进Sobel 算法提取边缘，对提取的边缘进行进一步处理得到喷胶点位，最后通过本文使用的新的标定算法对点位进行转换，所有步骤结合即为本文鞋底喷胶轨迹自动生成算法。

最后，本文对改进Sobel 算法边缘提取精度与普通Sobel 算法边缘提取精度进行对比实验，发现改进Sobel 算法边缘提取精度高于普通Sobel 算法边缘提取精度；此外，本文又对鞋底喷胶轨迹自动生成算法执行时间进行实验，发现鞋底喷胶轨迹自动生成算法执行时间均小于1 s，符合生产节拍需求；实际喷胶测试，总体喷胶合格率在96%左右。 符合生产需求。

1 系统总体方案

本文所处理的片底样式有两种，分别是16Q328与16Q329，如图1 所示。 每一种片底样式存在35 ～39 四个鞋码与左右脚，总共8 种不同的情况。

图1 片底样式Fig. 1 Sheet bottom style

2 边缘提取算法

2.1 图像预处理

图像预处理过程流程如图2 所示。

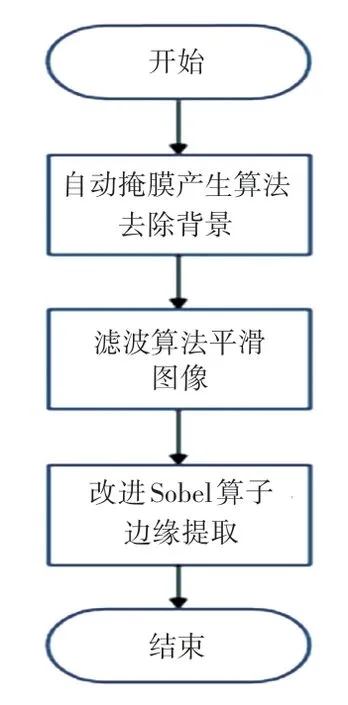
图2 图像预处理过程流程图Fig. 2 Flow chart of the image preprocessing process

由于相机采集得到的图像的背景比较复杂，对边缘提取会产生很多的干扰。 本文提出自动掩膜生成，在覆盖所需片底的情况下尽可能减少图片的背景。 由于片底的颜色为黑色，与周围环境的像素值有较大的差异，通过大量的测试数据发现片底区域的像素分布在0～150 范围内，而背景区域的像素分布在151～255 的范围内。 故通过像素分布的特征，设计自动掩膜生成特征区域，使得掩膜部分可以完全包括片底。

设原图像为G，产生掩膜图像M步骤如下：

Step 1设置一个筛选的最小与最大的像素阈值，本文选择像素阈值范围为（0＜Pixel＜150）；

Step 2对满足像素阈值范围的点进行分析，计算出所有点行的最小值、列的最小值、行的最大值及列的最大值；

Step 3将行的最大值与行的最小值相减再除以2，将行的最大值与列的最小值相减再除以2，得到掩膜矩形的中心点坐标；

Step 4将行的最大值与行的最小值相减后的值加上60 作为矩形掩膜的长，将列的最大值与列的最小值相减后的值加上60 作为矩形掩膜的宽（加上60 是为了保证矩形掩膜可以覆盖整个片底区域）；

通过自动掩膜生成的方式产生一个矩形掩膜，将矩形掩膜图像与原图进行或运算，或运算得到结果图记为O，或运算的计算，式（1）：

为使片底区域与背景的对比度更大，方便后续的边缘提取，先将或运算后图像中鞋底的区域进行填充，将原先像素分布在0 ～150 范围之内的像素点都填充为0。 填充步骤如下：

Step 1计算图像中像素在0～150 的点；

Step 2将满足Step1 的点的像素都变为0。

将填充后图像记为F，填充后图像如图3 所示。

图3 填充后图像FFig. 3 Post-fill image F

2.2 边缘提取

为得到准确的片底边缘信息，本文对传统的Sobel 算子做了改进，在边缘提取之前增加滤波操作来平滑片底边缘。 在边缘提取过程中采用8 个不同的卷积算子对图像8 个方向进行卷积操作，以防止图像的边缘出现断裂情况。 完成边缘提取后，增加边缘细化操作，将多余的边缘像素剔除掉，以便得到更加细致光滑的边缘。

2.2.1 均值滤波

对预处理后的图像F使用均值滤波器进行均值滤波，使得鞋底边缘更加平滑，以便于后续边缘提取的准确性。 采用以下3×3 卷积核对图像进行滤波操作，将滤波后图像记为G。 将目标矩阵与卷积核相乘得到新的矩阵卷积矩阵G（x，y），式（2）：

其中，F（x，y） 是填充后图像F中目标点与目标点周围8 个点，共9 个点组成的目标矩阵。

将得到的G（x，y） 矩阵中的9 个元素取出相加后取平均值即为目标点像素值。 通过计算得到所有点滤波后像素值即可组成新的滤波后图像G。 为了便于边缘提取，将滤波后图像中周围黑色无关部分进行了剔除，滤波后图像如图4 所示。

图4 滤波后图像GFig. 4 Filtered image G

2.2.2 8 方向边缘检测

本文共使用8 个方向的边缘检测算子，从不同的方向进行数据提取，每个方向的卷积算子卷积核如式（3）～式（10）所示，8 方向边缘检测结果如图5所示。

图5 8 方向边缘检测结果Fig. 5 Eight-way edge detection results

因为整个图像采用8 个方向的检测值，用原有方法计算各个方向梯度的时间复杂度比较高。 为了减少计算量，本文采用式（11）计算某一个点的像素值S（x，y）：

2.2.3 边缘细化

为得到更加细致的边缘，本文对Sobel 算子得到的边缘进一步边缘。 图像像素点8 连通域如图6所示。

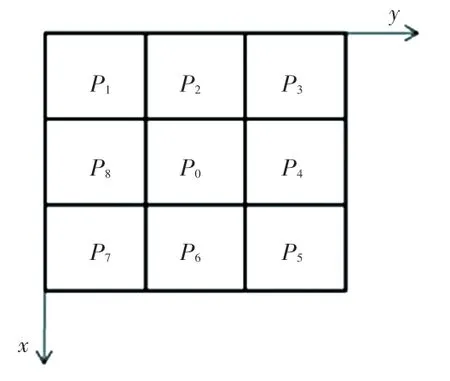
图6 8 连通域Fig. 6 Eight-linked domain

在完成边缘提取后得到的图像中，边缘部分像素为255，其他地方像素均为0，对Sobel 算法所提取的所有边缘点P0进行细化的步骤如下（E（P0） 表示P0周围像素为0 的点的个数）：

Step 1首先检查边缘点P0周围8 个点像素是否全为0，若E（P0）＝0，则判定这个点为离散点，直接剔除；

Step 2若满足如下条件，则标记P0为待剔除边缘点；

（1） 1 ≤E（P0） ≤7；

（2）P1＋P7＋P8≠0，P1＋P2＋P3≠0，P3＋P4＋P5≠0 且P5＋P6＋P7≠0；

Step 3一次循环遍历后，将标记为待剔除点像素置0，将其剔除。

Step1 与Step2 两步构成一次循环，多次循环执行Step1 与Step2 直到没有满足标记的条件为止。

在经过边缘细化后的边缘相比之前会变得更加细致，连续性也更高。

边缘提取结果如图7 所示，最终的边缘细化结果如图8 所示。

图7 边缘提取结果Fig. 7 Edge extraction results

图8 边缘细化结果Fig. 8 Edge refinement results

3 边缘点提取与转换

片底边缘细化后，对边缘特征点进行进一步的提取并转换，并将边缘点信息转变为机器人循迹所需要的实际点位信息。 具体的边缘点提取与转换步骤流程如图9 所示。

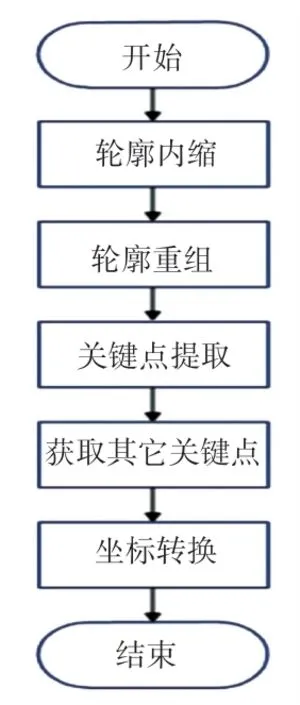
图9 边缘点提取与转换流程图Fig. 9 Edge point extraction and transformation flowchart

3.1 内缩轮廓

轮廓内缩需要将得到的轮廓以相同的距离往内侧收缩，形成一个新的内缩轮廓。 以边缘提取得到的轮廓中的每一个点为圆心，以自定义内缩半径为圆半径绘制圆形，将所有圆形区域所包含的所有点组成一张新的图像。 圆形公式（12）：

其中，（X0，Y0） 是圆心坐标，R为圆半径。

由于圆具有8 分对称性，圆心位于原点的圆有4 条对称轴X＝0、Y＝0、X＝Y和X＝-Y，若已知圆弧上一点P（X，Y），就可以得到其关于4 条对称轴的7 个对称点：（X，-Y）、（-X，Y）、（-X，-Y）、（Y，X）、（Y，-X）、（-Y，X）、（-Y，-X），这种性质称为8 分对称性。 因此只要能画出1／8 的圆弧，就可以利用对称性的原理得到整个圆。

假设轮廓上某个点为（0，0），圆半径大小为R，那么以这个（0，0） 点为圆心，R为半径的圆上的1／8弧上的点可以通过以下方式求得，这里以（0，R） 点作为起始点，顺时针计算1／8 圆弧。

圆函数如式（13）所示，将平面区域分成圆内和圆外，如图10 所示。

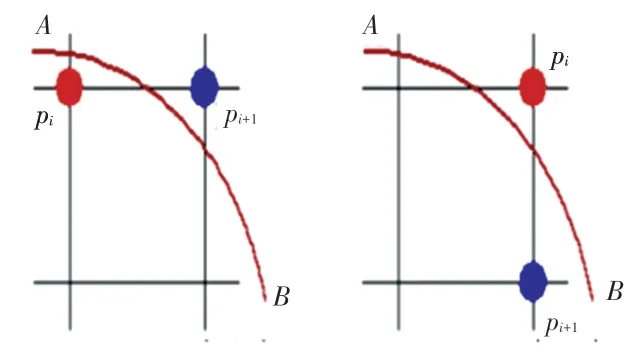
图10 圆内圆外示意图Fig. 10 Schematic diagram of the inside and outside of the circle

假设圆弧的生成方向是从A到B方向，当某个点Pi被确定以后，Pi的下一个点Pi＋1的取值就根据F（Xi，Yi） 的值进行判定，判定的原则：

（1）当F（Xi，Yi） ≤0 时，取Xi＋1＝Xi＋1，Yi＋1＝Yi，从圆内走向圆外；

（2）当F（Xi，Yi）＞0 时，取Xi＋1＝Xi，Yi＋1＝Yi-1，从圆外走向圆内。

对于判别式F（xi，yi） 的递推公式，也要分两种情况分别推算：

（1）当F（Xi，Yi） ≤0 时，Pi的下一个点Pi＋1取Xi＋1＝Xi＋1，Yi＋1＝Yi，判别式F（Xi＋1，Yi＋1） 的推算过程如式（14）所示；

（2）当F（Xi，Yi）＞0 时，Pi的下一个点Pi＋1取Xi＋1＝Xi，Yi＋1＝Yi- 1，判别式F（Xi＋1，Yi＋1） 的推算过程如式（15）所示。

在得到1／8 圆弧后，通过圆的8 分对称性即可得到整个圆所包含的点的信息。

通过循环的方式多次绘制外接圆，将每一个外接圆都进行填充变为一个区域，再求取每一个外接圆，形成区域的并集形成新的区域，新的拼接区域如图11 所示。 在得到新的拼接区域后，通过边缘提取算子可以得到新区域的内外轮廓，内外轮廓如图12所示。 通过比较两个轮廓的实际长度，长度较小的轮廓即为所需要的内缩轮廓。

图11 拼接区域Fig. 11 Splicing area

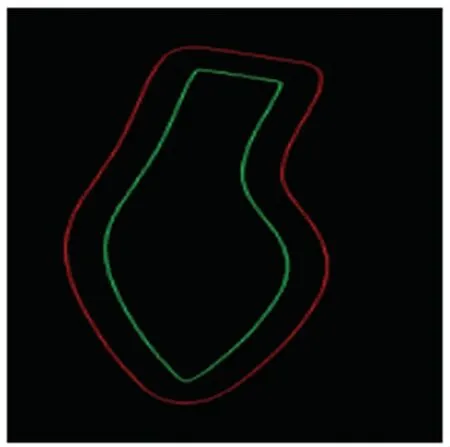
图12 内外轮廓Fig. 12 Inner and outer contours

3.2 轮廓重组

每一个内缩轮廓由多个离散的点拟合而成，经过测试发现不同角度鞋底图片得到的点的起始位置是不确定的，导致轮廓信息存在不确定性。 因为轮廓的起点无法确定，所以在执行后续处理算法前增加了将轮廓重组操作，轮廓重组以整个轮廓行最小值位置为起点，最小点基本处于鞋尖位置，故通过轮廓重组后的轮廓数组均可以鞋尖位置作为起点。

轮廓重组过程：假设原轮廓行数据数组为［TR0…TRend］，通过轮廓重组后得到的行数据数组为［TRmin…TRend…TR0］，其中［TRmin是行数据数组轮廓［TR0…TRend］ 中最小值所在索引位置，同样轮廓重组后得到列数据数组为［TCmin…TCend…TC0］ 。

通过重组操作不管鞋底角度如何变化，原轮廓起点在什么位置，新的轮廓的起点都确定在鞋尖位置。

3.3 关键点提取

在每一次轨迹生成时，都需要知道鞋底、鞋跟两个点的位置与鞋尖点的位置，这3 个点为整个轮廓的转折点，需要提前取得。 通过绘制内缩轮廓外接圆的方式可以得到内缩轮廓的外接圆，再求取外接圆与内缩轮廓的交点，其中一个交点为鞋尖点，另一个交点为左侧鞋跟交点。 由于在实际操作时确定了鞋底来料的大致方向，所以在图像窗口中鞋底永远在上方，可以保证鞋底点的行坐标永远都是小于鞋尖点的行坐标，通过比较两个交点的行坐标即可确定鞋尖点和鞋跟点。

通过大量测试轮廓总点数与鞋跟两侧所隔点数的关系可以获得一个拟合方程，式（16）：

其中，［Distance］ 是取整后的距离，PointT是外轮廓点数。

通过计算得到鞋跟右侧交点与左侧交点所隔点的数量，从而在轮廓数组中找到右侧交点。 得到的3 个关键点如图13 所示。

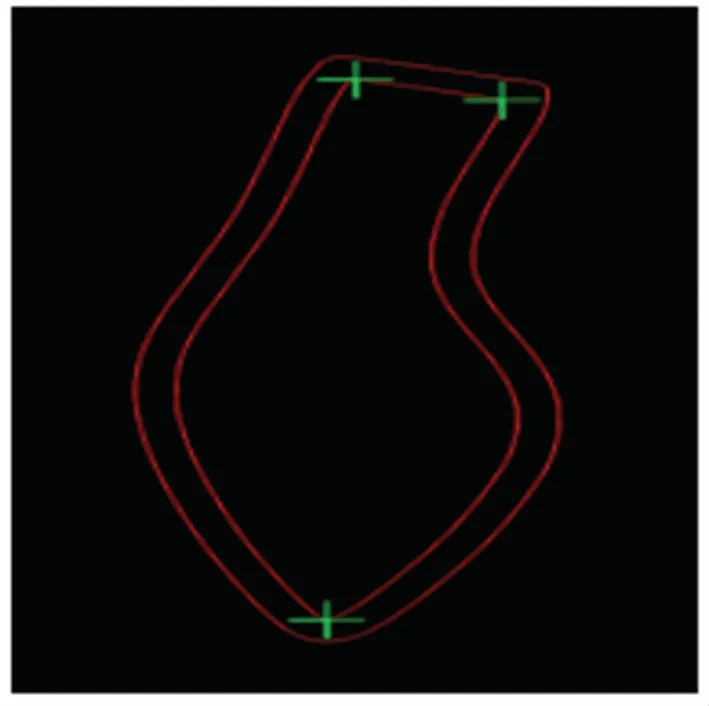
图13 3 个关键点Fig. 13 Three key points

3.4 获取其他关键点

在得到了3 个关键点之后，通过其在轮廓数组中的索引的位置即可得到其它位置轨迹点的信息，将轨迹点进行组合就可以得到完整的轨迹信息，得到的轨迹如图14 所示。

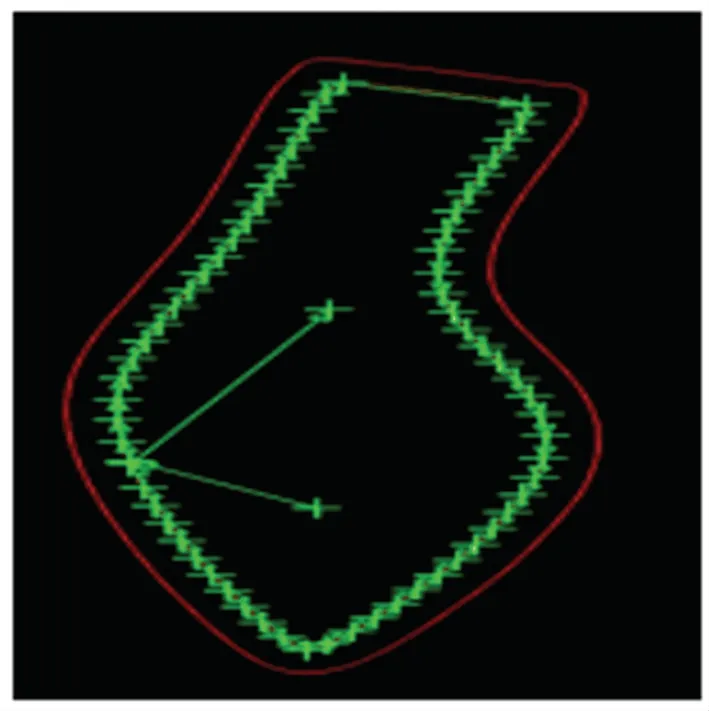
图14 全部点与轨迹Fig. 14 All points and trajectories

3.5 坐标转换

首先在鞋底中绘制9 个固定点，将鞋底放置在相机下进行图像采集。 在图像坐标中找到之前手动绘制的9 个固定点，并记录下9 个点的行列坐标值，再将机器人移至9 个固定点，记录实际机器人TCP（Tool Center Position）的X／Y值。

通过式（17）即可计算得到图像坐标系中点位与实际机器人坐标系之间的转换关系。 本文为了使得转换矩阵更加的准确，在标定过程中选择9 个点作为标定点。

通过计算式（17）即可得到转换矩阵H，有了转换矩阵H就可以把图像坐标系上任意一个点坐标变为实际的机器人世界坐标系下的点坐标。

4 实验

实验所使用的计算机配置为：工控机CPU 为AMD Ryzen5 4600H，内存条为两个Hynix 的8 GB内存条，频率为4 600 MHz，软件使用编译器为VS2019，框架为NET 4.6.1。

4.1 改进Sobel 算子边缘精度实验

对普通Sobel 算法与本文所提出的改进Sobel算法的边缘检测准确性进行比较，将提取的边缘点数据进行坐标转换后转为实际机器人可以使用的实际坐标，并通过移动机器人比较两个算法的准确性。

本文做边缘准确度实验所取的边缘点数均为40 个，每一次的误差值是所有40 个点中每个点到真实边缘距离的平均值。 测试方式为机器人走至算法给出的边缘点，再通过人为操作机器人控制器将机器人TCP（Tool Center Position）移至实际边缘记录算法给出的Xf／ Yf值与控制器上实际边缘的Xr／Yr值。 通过计算得出每一个点的误差值，式（18）：

本文总共进行了100 次对比实验，普通Sobel算法边缘提取与改进后Sobel 算法边缘准确度对比如图15 所示。

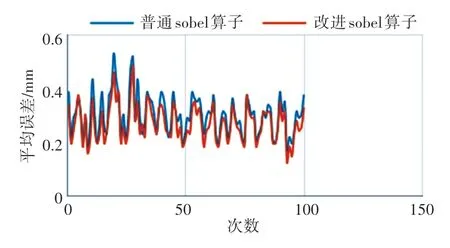
图15 边缘检测准确度对比图Fig. 15 Edge detection accuracy comparison chart

实验结果表明，普通Sobel 算法的平均边缘提取误差为0.248 3，而改进后Sebel 算法的平均边缘提取误差为0.223 8，更加符合精度需求。

4.2 算法执行时间实验

对不同鞋型鞋码的片底进行随意旋转（旋转角度控制在0°～180°之间），对不同位置与角度的片底进行轨迹提取。 本文总共对1 000 张不同样式角度的鞋底进行轨迹提取，算法运行时间统计如图16 所示，在1 000次算法执行实验中算法执行最长耗时为0.990 s，最短耗时为0.416 s，大多数算法执行时间在0.4～0.8 s 之内，提取结果算法均十分理想，且所有算法执行时间都控制在1 s 之内，经计算1 000算法执行的平均时间为0.661 1 s，符合生产所需要速度要求。

图16 算法运行时间结果Fig. 16 Algorithm runtime results

部分轨迹提取结果如图17 所示。

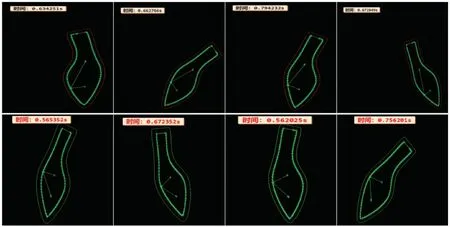
图17 部分轨迹提取结果Fig. 17 Partial trajectory extraction results

4.3 实际喷胶实验

本文对片底进行了实际喷胶测试。 经过500 次喷胶测试，在500次的喷胶结果中合格样品数量达到480 只，总体的合格率高达96%符合生产要求。

5 结束语

本文针对当前3D 相机处理片底价格昂贵且边缘提取精度不高的问题，提出了通过使用2D 相机的方式来提取轨迹。 通过改进边缘提取算法得到准确度更高的边缘轮廓，并通过边缘点提取算法从边缘轮廓中获取喷胶点位数据；最后，通过坐标转换算法将图像点位数据转为实际机器人喷胶点位。

在不影响精度的情况下，如果可以找到更快速得到内缩轮廓的方式，可以使得轨迹生成的速度控制在0.5 s 之内。 目前的执行速度已经可以满足生产的要求，从算法执行时间的测试数据来看，每一次的算法执行速度都控制在了1 s 之内，加上皮带运行时间和机器人加工时间，全自动喷胶的总体速度也可以控制在5 s 之内，且最终的喷胶稳定性也符合生产要求，相比人工有很大的提升。