应用于MMC 换流阀的新型子模块电容电压波动抑制策略

杨银国，于珍，李力，刘洋，陆秋瑜

（广东电网有限责任公司电力调度控制中心，广州 510030）

0 引言

近年来，海上风电因其资源丰富、利用效率高、不占用土地资源等优点而备受关注，海上风电在中国得到迅速发展［1-5］。在远距离输电场景下，考虑到电缆的电容电流，传统的交流输电在技术上和经济上都不具有吸引力。因此高压直流输电被认为是大容量远海风电并网最合适的选择［6-9］。

模块化多电平换流器（multilevel modular converter，MMC）具有控制灵活、运行损耗低、无换相失败、谐波畸变率小等优点，适用于高压大功率的远海风电并网等场景。目前，基于MMC 的高压直流输电技术，即柔性直流输电已被长距离的海上风电并网所采用，国内外已有多条海上风电柔直送出工程建成投运。然而，MMC 换流阀中子模块电容占子模块体积的50%以上、成本的40%左右，使得目前建成的海上换流站的重量在14 500~25 000 t之间，导致了较高的建造和维护成本［10-11］。子模块电容容值的大小与电容电压波动幅值的大小密切相关，在此背景下，研究适用于海上风电场景下的MMC 子模块电容电压波动抑制策略，降低对电容容值的需求，从而减小海上换流平台的体积和成本，具有重大的工程意义。

目前，国内外专家学者对于半桥MMC 电容电压波动抑制策略的研究已取得一定成果［12-14］。对于环流抑制类，文献［15］设计了稳态下的环流抑制控制器，有效地抑制了桥臂上的二倍频环流。文献［16］提出了一种通用的环流抑制策略，适用于稳态和三相不平衡的工况，但其控制难度增加，控制精度有所降低。文献［17］设计了基于PR 控制器的环流抑制环节，但其稳定性有待提高。环流抑制类方案是通过将桥臂的二倍频环流抑制到零来降低子模块的电容电压波动，其抑制效果较为有限。对于环流注入类，文献［18］通过离线优化计算得到电容电压波动最小时的二倍频环流幅和相角。文献［19］通过消去桥臂功率的二次谐波分量，计算得到经典的二倍频环流参考值，有效降低了子模块电容电压波动。文献［20］提出了一种利用瞬时信息在线计算环流参考值的方法，避免了查表法确定环流注入量，提高了其工况适应能力。对于三次谐波注入类，文献［21］提出在桥臂参考波上注入三次谐波电压可以降低参考波峰值，提高了直流电压利用率和调制比m，从而抑制电容电压波动，并推导得出了三次谐波电压注入的幅值和相角。文献［22］分析了三次谐波电压注入对MMC 运行特性的影响，并优化了注入的幅值和相角参数，但只考虑稳态工况，未考虑其他工况下策略的适用性。文献［23］提出了适用于单相接地故障的三次谐波注入方法，但是该方法需要利用全桥子模块的负电平输出能力，不适用于半桥MMC 拓扑。然而，三次谐波电压的注入会很大程度地影响二倍频环流的注入参数，且MMC 桥臂电流与电压调制波的交互过程较为复杂，这两类抑制策略之间具有强耦合性，加之离线计算谐波注入参数的方式不适合海上风电工况频繁变化的场景，需要对两者的协同注入方法以及谐波注入对MMC运行特性的影响展开研究。

本文针对半桥MMC 提出了一种抑制子模块电容电压波动的谐波协同注入策略。首先分析了二倍频环流和三次谐波电压协同注入对子模块电容电压波动和MMC 运行特性的影响，并根据半桥MMC的调制比范围和桥臂损耗给出注入参数的约束条件。基于对子模块电容电压的基频和二倍频波动分量的分析，给出了谐波协同注入参数的优化结果。最后，依靠PSCAD 平台搭建了仿真模型，验证了理论分析的正确性和所提策略的有效性。

1 谐波协同注入对子模块电容电压波动的影响

半桥型MMC拓扑结构如图1所示。其中，每相上下桥臂各有N个半桥子模块，uj（j=a，b，c）为AC侧相电压，Udc为DC侧电压，ipj和inj分别为每相上下桥臂电流，upj和unj分别为每相上下桥臂电压，Idc为直流电流，Rarm和Larm分别为桥臂电阻和桥臂电感。

图1 半桥型MMC拓扑Fig. 1 Topology of the half-bridge MMC

谐波协同注入方法是指在桥臂电流上注入二倍频环流且在AC 侧注入三次谐波电压。二倍频环流和三次谐波电压将会影响MMC 原本的电压电流特性，从而影响子模块电容电压波动。根据图1 的参考正方向，以A 相为例，注入二倍频环流后，桥臂电流中包含直流分量Idc、基频分量Im1以及二倍频分量Im2，表达式如下。

式中：ω为基波角频率；Im1为基频电流分量幅值；Im2为注入的二倍频电流分量幅值；φ2为二倍频电流相角。

注入三次谐波电压后，调制波的波形会发生改变，A相调制波的表达式为：

式中：m=2Um1/Udc，定义为电压调制比；m3=2Um3/Udc，定义为三次谐波电压调制比；Um1和Um3分别为交流测相电压幅值和三次谐波电压幅值；φ和φ3分别为功率因数角和三次谐波电压相角。

根据KVL，A 相上下桥臂参考电压的表达式如下。

定义Spa和Sna分别为A 相上下桥臂的开关函数［24］，开关函数的表达式如式（4）所示。

假设MMC 各子模块之间的均压良好，则桥臂电流、开关函数与子模块电容电压平均值之间有以下关系。

式中：C为子模块电容容值；upa_ave和una_ave分别为A相上桥臂和下桥臂的子模块电容电压平均值。

由于二倍频环流和三次谐波电压的注入，子模块的电容电压会增加额外的谐波分量。以上桥臂为例，将式（1）、（4）代入式（5）中，可以得到桥臂子模块的电容电压平均值的具体表达式如式（6）所示，其中N为桥臂模块个数。由于子模块电容能量不能无线累积，式（6）中上下桥臂子模块电容电压的直流分量应该为0，由此可以得到交直流侧电流的关系，如式（7）所示。

观察式（6）可以发现，二倍频环流和三次谐波电压的协同注入能够影响子模块电容电压的基频和二倍频波动，并额外产生了更高次的谐波分量。其中，上下桥臂的奇数次波动量方向相反，交流侧电压会产生对应频率的波动；上下桥臂的偶数次波动量方向相同，且三相间具有正序关系，因此在MMC 每相桥臂会产生对应频率的正序环流，因而直流侧电压也会产生对应频率的波动。由于谐波协同注入的幅值较小，高次谐波分量频率较大，所以电容电压的波动主要是由基频和二倍频分量组成，且高阶偶数次环流频率较大，桥臂电感的电抗较大，因此高阶环流的幅值较小，不会对MMC 的稳态运行造成大的影响。

2 谐波协同注入对MMC 运行的影响及约束条件

第1 节主要分析了谐波协同注入后对子模块电容电压的影响，本节针对谐波协同注入后的调制波和桥臂电流的变化，对注入参数的约束条件进行分析。

由于半桥子模块不具备全桥子模块的负电平输出能力，因此半桥MMC 稳态运行时的电压调制比范围一般为0.8~1［25］，考虑到半桥MMC 正常运行的调制范围约束，需要对注入三次谐波电压的幅值进行讨论。图2 为三次谐波电压注入后的调制波波形。

图2 调制波波形Fig. 2 Waveforms of the modulated waves

从图2 可以看出，若三次谐波电压的注入幅值选取不合适，就会导致调制波超出约束范围，影响MMC 的正常运行，以上桥臂为例，本文对三次谐波电压调制比m3的约束如下。

根据式（3），三次谐波电压注入前，桥臂参考电压的正负峰值Upa_max和Upa_min如式（8）所示。

注入三次谐波电压之后，桥臂参考电压的正负峰值Upa3_max和Upa3_min变为：

桥臂参考电压达到峰值等同于开关函数达到峰值，其对应的时间tmax的求解过程如式（10）所示。

令式（10）等于0即可求得峰值时刻tmax，在系统稳态运行时，tmax为m3和φ3的函数，将tmax代入式（3）即可得到桥臂参考电压的正峰值和负峰值。

桥臂参考电压不能超出半桥MMC的运行范围，因此，三次谐波电压调制比m3应满足的关系为：

对二倍频环流注入参数的约束主要是考虑换流阀损耗和系统稳定性的问题，环流较大时会增大桥臂的电流应力，引起直流侧的振荡，同时也会增加换流阀的损耗。

图3 为二倍频环流注入前后的桥臂环流。若注入的环流参数不合适，桥臂环流甚至会大于不采用策略时系统本身的环流，对MMC 的运行也会造成一定的影响。本文以此为约束条件，即环流注入的幅值Im2不大于不采用策略时系统的环流［22］。

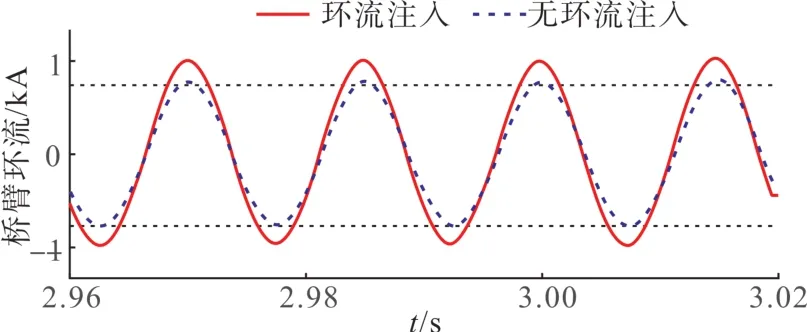
图3 桥臂环流Fig. 3 Circulating current of the bridge arm

式中：Larm为桥臂电抗；I2f为系统环流。

需要说明的是，受到半桥MMC 调制比范围的限制，三次谐波电压的约束条件必须满足，否则会影响MMC 的正常运行，而二倍频环流的约束主要考虑的是桥臂损耗增加的问题，在进行合理的经济性评估后可适当放宽。

3 谐波协同注入优化策略

3.1 建立优化目标函数

根据式（6）—（7），上桥臂子模块电容电压波动的基频和二倍频分量upa_ave1和upa_ave2可以表示为：

式中m2=Im2/Im1定义为二倍频环流注入系数。

为了使得电容电压波动最小，应满足基频和二倍频波动分量为0，即：

通过分析第2 节给出的注入参数的约束条件以及半桥MMC 调制比的限制，对于基频波动分量，无法将其抑制到0。因此，本文选择的抑制策略是将二倍频分量抑制为0 的基础上，尽可能地抑制基频分量。为了将二倍频分量抑制为0，协同注入参数需要满足以下关系。

在满足子模块电容电压二倍频分量抑制到0 的同时，要保证基频分量最小，此时的基频波动分量upa_ave1为：

将上式通过三角变换，可以改写为：

式中M1和M2为正余弦系数，具体的表达式如下。

由式（18）可以得到电容电压基频波动的幅值|upa_ave1|为：

考虑到约束条件的限制，以最小化电容电压基频波动幅值为目标，构建目标函数如式（20）所示。

3.2 参数优化结果

根据式（20）可知，对目标函数g（m2）的优化过程是针对二倍频环流注入参数m2进行的。为了验证本文策略对不同工况的适用范围，本节列举了MMC 多种运行工况下环流注入参数的优化结果，如表1所示。

表1 环流注入参数优化结果Tab. 1 Optimization results of circulating current injection parameters

从表1 的优化结果可以看出，功率因数影响环流注入参数的大小，功率因数越大，最优的环流注入参数相对越小，而电压调制比对于参数的优化结果基本没有影响。由于MMC 在实际运行时功率因数接近于1，因此谐波协同注入的参数值设置如下。

从式（21）可以看出，谐波协同注入的幅值参数为定值，从而避免了由于功率因数变化需要重新计算谐波注入参数的情况，对于工况多变的场景更具有适用性。

谐波协同注入的控制框图如图4 所示。根据式（21）的参数优化结果，生成对应的二倍频环流和三次谐波电压参考信号，最终通过改变调制波，实现谐波协同注入。

图4 谐波协同注入控制框图Fig. 4 Control block diagram of coordinated harmonic injection

4 仿真分析

4.1 系统参数

为了验证所提的谐波协同注入策略的有效性，在PSCAD 仿真平台搭建了双端MMC 模型，MMC具体参数见表2。

表2 仿真模型参数Tab. 2 Parameters of the simulation model

4.2 仿真结果

首先以运行工况m=0.8，cosφ=1为例进行仿真分析。2 s 之前投入文献［15］中的环流抑制策略，2 s 时投入本文的谐波协同注入策略，仿真结果如图5所示。

图5 仿真结果（m=0.8，cosφ=1）Fig. 5 Simulation results （m=0.8, cosφ=1）

图5（a）为MMC 网侧交流电压，由于海上换流站联接变一般采用（网侧）Yn/d11（阀侧）接线方式，阀侧注入的三次谐波电压不会影响网侧电压，因此谐波注入前后网侧交流电压波形保持不变。图5（b）所示的是MMC 阀侧交流电压，三次谐波电压的注入重塑了交流电压的波形。图5（c）是MMC 三相上桥臂的子模块导通个数，2 s 投入谐波协同注入策略后，没有出现子模块负投入的情况，说明所提策略能够满足半桥MMC 的调制比约束范围，不会影响其正常的调制过程。图5（d）所示的是三相上桥臂电流，策略投入后，桥臂电流中增加了二倍频的环流分量。图5（e）所示的是三相子模块电容电压的平均值，从图中可以看出，应用环流抑制策略时，电容电压波动的峰值为470 V，而应用本文的协同注入策略之后，其峰值降为335 V，相较于经典的环流抑制策略，能进一步抑制28.72%的电容电压波动。

表1 所示的优化结果表明，电压调制比m不会影响注入参数的选取，且当功率因数较大时，谐波注入的参数也相同，下面通过仿真来验证本文策略对不同运行工况的适用性。图6 和图7 所示的分别是电压调制比和功率因数对所提策略的影响分析。

图6 电压调制比影响分析Fig. 6 Effects analysis of voltage modulation indexes

图7 功率因数影响分析Fig. 7 Effects analysis of power factors

图6 所示为功率因数相同，调制比不同的4 种运行工况下的子模块电容电压平均值。图6（a）为m=0.8，cosφ=1，根据前文分析，相较于环流抑制策略，此工况可进一步抑制28.72%的电容电压波动。图6（b）为m=0.85，cosφ=1，应用环流抑制策略时，电容电压波动的峰值为405 V，而应用本文的协同注入策略之后，其峰值降为290 V，能进一步抑制28.40%的电容电压波动。图6（c）为m=0.9，cosφ=1，应用环流抑制策略时，电容电压波动的峰值为385 V，而应用本文的协同注入策略之后，其峰值降为245 V，能进一步抑制36.36%的电容电压波动。图6（d）为m=0.95，cosφ=1，应用环流抑制策略时，电容电压波动的峰值为345 V，而应用本文的协同注入策略之后，其峰值降为220 V，能进一步抑制36.23%的电容电压波动。经过对比发现，本文策略在不同的电压调制比下都具有很好的电容电压波动抑制效果，电压调制比越大，其抑制效果越明显。

图7 所示的为电压调制比相同，功率因数不同的4 种运行工况下的子模块电容电压平均值。图7（a）为m=0.8，cosφ=1，相较环流抑制策略，此工况可进一步抑制28.72%的电容电压波动。图7（b）为m=0.8，cosφ=0.95，应用本文的协同注入策略之后，能进一步抑制28.85%的电容电压波动。图7（c）为m=0.8，cosφ=0.9，应用本文的协同注入策略之后，能进一步抑制24.56%的电容电压波动。图7（d）为m=0.8，cosφ=0.8，应用本文的协同注入策略之后，能进一步抑制18.25%的电容电压波动。经过对比发现，本文策略在不同的功率因数下都具有很好的电容电压波动抑制效果，功率因数越大，其抑制效果越好。

图8 给出了两种策略下子模块电容电压的频谱分析结果。可以看出基频和二倍频分量是电容电压波动的主要影响因素，本文策略能够进一步抑制电容电压的基频和二倍频波动分量。谐波协同注入的同时，也会产生三次及三次以上高次谐波分量，但其幅值相对于基频和二倍频分量较小，可以忽略，与式（6）的理论分析结果一致。

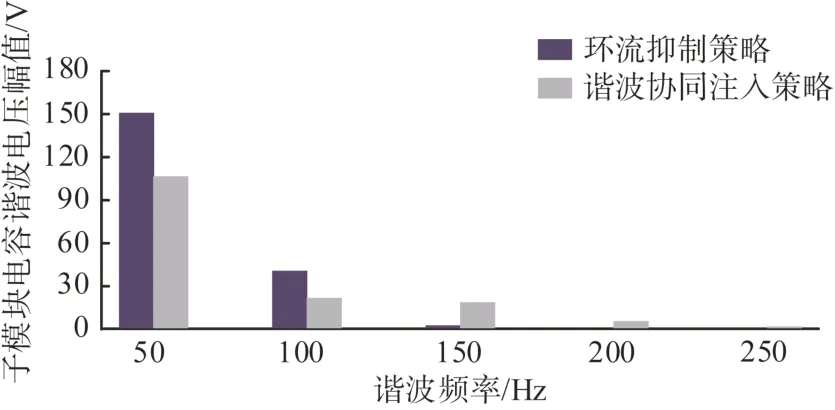
图8 子模块电容电压频谱图Fig. 8 Spectrum diagram of sub-module capacitor voltage

5 结论

本文针对半桥MMC 提出了一种抑制子模块电容电压波动的谐波协同注入策略，得到结论如下。

1） 所提谐波协同注入策略能够有效抑制子模块的电容电压波动，同时仅产生幅值很小的高阶谐波分量，对MMC其他的运行特性影响很小。

2） 所提策略的谐波协同注入的参数是定值，当工况发生变化时不需要重新计算谐波注入参数，适用于功率变化频繁的场景。

3） 所提策略对于不同的运行工况有较强的适应能力，在多种不同的电压调制比和功率因数的工况下都能有效地抑制子模块电容电压的波动。

与目前已有的谐波注入策略相比，所提策略的局限性总结如下。

1） 所提策略是针对半桥型MMC 提出的，考虑了其运行调制比的限制；当拓扑类型为混合型或全桥型MMC 时，需要放宽其调制比约束并重新计算注入参数。

2） 所提策略为稳态下的注入参数，当系统发生故障时，需进一步研究所提策略的适用性，分析暂态和稳态特性之间的差异，推导计算暂态下的注入参数。