风电经柔性直流组网系统受端交流故障过电压分析及穿越策略

王振浩，王欣铎，李金伦，李国庆

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林 吉林 132012）

0 引言

基于模块化多电平换流器（modular multilevel converter， MMC）的柔性直流（以下简称“柔直”）输电具备控制方式灵活、无需强电网支撑以及可实现多电源供电和多落点受电等独特的技术优势［1］，成为大规模风电多区域汇集、远距离输送的有效方案。

近年来，大规模风电经柔直组网外送方案因其供电可靠性高，单位输电成本低，受到了广泛的关注，但由于其网架互联特性，局部故障反而更加容易通过线路扩散到整个系统［2-3］。一旦系统发生受端交流故障，柔直电网的功率送出能力大幅度降低，由于风电场在故障期间仍会持续向柔直电网注入功率，柔直电网将持续累积不平衡能量，导致直流电压在数十毫秒内越过安全界限，触发过电压保护，进而导致换流站闭锁，对整个系统造成较大冲击。因此，提出有效策略使系统在受端交流故障期间安全稳定地持续运行是风电经柔直组网外送方案面临的关键问题之一。

目前针对受端交流故障穿越策略的研究主要包括配备耗能装置和风电场降载两种方法，其中最直接有效的解决方法就是配备耗能装置。交流耗能装置［4-5］一般采用反并联晶闸管与耗能电阻串联组成，经降压变分组安装在送端换流站的交流侧，其单组容量越小，功率控制精度越高，电阻投切对直流电压的冲击越小，但工程成本也会相应提高。早期的直流耗能装置［6-7］一般采用多个绝缘栅双极型晶体管（IGBT）与耗能电阻串联组成，装设在直流线路上，通过设定直流电压上下阈值的方式来控制其投切以耗散故障导致的不平衡能量，但随着直流电网电压等级的提高，对IGBT串联阀提出更高的技术要求。为了解决IGBT直接串联带来的技术问题，文献［8-9］提出了模块化耗能装置的方案，每一个耗能装置模块都可独立投切，提高了耗能装置的可靠性，但该方案提高了耗能装置的造价。文献［10］将耗能电阻分置在各子模块中，该方法虽能节省占地成本，但该方法增大了子模块的制造难度，而且耗能电阻的投切控制较复杂。近年来，针对风电场降载控制策略的研究也取得较大进展。文献［11-12］提出基于快速通信法的风电场降载控制策略，但该策略对通信系统的可靠性、快速性提出更高要求，通信成本较高。文献［13-14］提出了降低风电场侧电压和升高风电场侧频率两种无需通信的风电场降载控制策略，当送端换流站采用交流电压单闭环控制时，降压法可以快速响应，但该策略下风电场快速降载可能会导致换流站闭锁；而升频法要求风电机组具有快速的频率响应特性，且频率的快速变化可能造成风电场脱网［15］。文献［16］在提出故障后提高风机转子转速降低机组有功出力的控制策略，但因风力机惯性较大，该控制策略难以快速降载，在面对严重的故障场景时，难以单独完成故障穿越。

综上所述，配备耗能装置虽能够满足大多数工况下受端交流故障的穿越要求，但其工程造价、占地面积、散热成本都是该方法面临的主要问题。风电场降载控制策略虽能够节约造价和占地，但一般存在响应时间较长、降载效果有限的缺陷，难以单独完成受端交流故障的穿越。因此，针对大规模风电经柔直组网的场景，需要提出一种既能满足大多数工况下受端交流故障的穿越要求，又可以降低部分成本的受端交流故障穿越策略。

在此背景下，本文基于MMC的基本工作原理，首先从能量平衡的角度详细分析了受端交流故障下柔直电网的暂态过电压机理，其次根据故障期间直流电压的表达式提出一种具备限压功能的自适应最近电平逼近策略（adaptive nearest level modulation，ANLM）策略，并将其与传统最近电平逼近策略（nearest level modulation， NLM）策略进行了对比分析；随后给出ANLM策略与风电机组内部斩波电阻协同配合的受端交流故障穿越策略。与其他故障穿越策略相比，所提策略仅利用换流站的储能潜力和风电机组的自身响应，不增设额外设备，大大地降低了穿越成本。最后，在PSCAD 仿真软件中，构建了风电经四端柔直组网系统的仿真模型，对所提策略的有效性进行了验证。

1 大规模风电经柔直组网系统结构和MMC基本工作原理

1.1 大规模风电经柔直组网系统结构

基于永磁同步发电机（permanent magnet synchronous generators，PMSG）的大规模风电场经柔直组网系统采用运行方式灵活的四端真双极环形接线，各换流站信息如表1 所示。系统结构如图1所示。

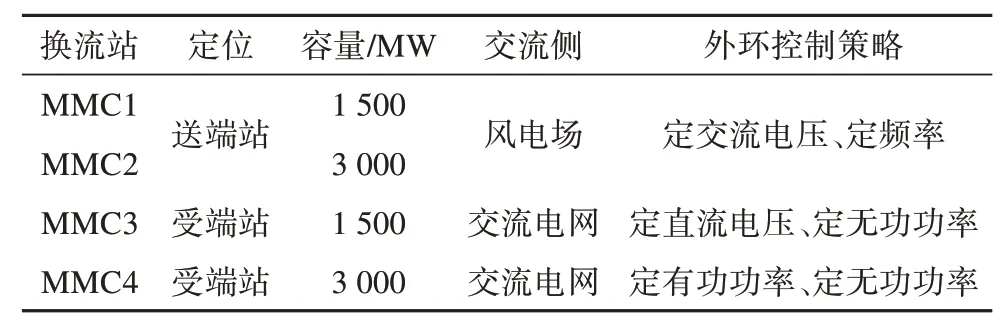
表1 各换流站的基本信息Tab. 1 Basic information for each converter station

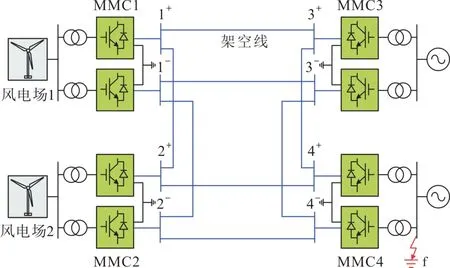
图1 大规模风电经柔直组网系统结构Fig1 System structure of large-scale wind power connected to flexible HVDC grid

1.2 半桥型MMC基本工作原理

柔直工程中常用的半桥型MMC 结构如图2所示。

图2 MMC基本结构图Fig. 2 Basic structure of modular multilevel converter

每相上、下桥臂均由N个半桥子模块（halfbridge sub-module，HBSM）、一个桥臂电阻和一个桥臂电抗串联组成。半桥型MMC多采用NLM 策略作为其调制方式。首先，NLM 策略控制MMC 单相桥臂投入的子模块数量始终为N，确保MMC 直流侧电压Ud大小恒定。其次，NLM 策略通过控制桥臂子模块的投切生成相应的交流侧三相电压波形。MMC的交直流侧电压满足式（1）。

式中：M为MMC 输出的调制比；usm为MMC 交流侧输出电压的目标值，只有当M在0~1 区间内时，MMC交流侧才会输出理想的交流电压。

2 风电经柔直组网系统受端交流故障暂态过电压机理分析

2.1 系统稳态运行分析

设存在一个由m（m≥3）端换流站构成的柔直电网，各站均采用矢量电流控制，各站可实现交流侧有功功率和无功功率的独立控制［17］。对于大规模风电经柔直组网的场景，稳态运行时，送端换流站需为风电场并网提供可靠的电压，即交流侧电压v的d、q轴分量在送端站的控制下保持不变，其汇集的风电功率仅与风电场出口电流i有关，如式（2）所示；受端换流站交流侧电压由其连接的交流电网给定，本身可以通过控制id，RE和iq，RE实现对其交流侧有功功率p的主动控制，如式（3）所示。

式中：pSE和pRE分别为送端换流站和受端换流站的交流侧有功功率；qSE和qRE分别为送端换流站和受端换流站的交流侧无功功率；vd，SE、vq，SE分别为送端换流站交流侧电压v的d、q轴分量；id，WF、iq，WF分别为风电场出口电流的d、q轴分量；vd，GS、vq，GS分别为受端交流电网交流侧电压v的d、q轴分量；id，RE、iq，RE分别为受端换流站交流侧电流的d、q轴分量。

系统稳态运行时，各换流站的储能保持动态平衡，各站交直流侧与子模块之间进行周期性的电能存储与释放，仅为其交直流侧提供了一个能量相互交换的场所，在一个交流电压周波T内，整个柔直电网能量平衡表达式（4）所示。

式中：Pi为各换流站直流侧功率，i=1，2，3，…，m；pi为各换流站交流侧功率；Ploss为柔直电网的网损。

2.2 暂态过电压机理

当系统发生受端交流故障后，其送出有功功率会持续下降，由式（4）可知，若期间送端换流站交流侧持续汇集的有功功率大于受端换流站剩余的功率传输极限，柔直电网内会持续累积不平衡能量，换流站作为柔直电网内的主要储能装置，承担起暂时存储不平衡能量的任务。

受端交流故障期间，与子模块电容储能变化相比，换流站中桥臂电感的储能变化极小，为简化分析，可将换流站储能近似为子模块电容的储能［18］。

在受端交流故障期间，电容电压排序与均压算法的共同作用，各站内6N个子模块交替投切，子模块电压轮流升高，最终实现对不平衡能量的吸纳。

设t=0 时刻故障发生，则在故障期间柔直电网内的子模块电容电压持续抬升过程的表达式如式（5）所示。

式中：ΔP∑为整个柔直电网中的不平衡功率；N为子模块数量；m为换流站数量；子模块C0i为各换流站的子模块电容值；UC(t)为t时刻子模块电容电压；UC(0)为t=0时刻子模块电容初始电压。

由于定直流电压站的调节速度慢于子模块电容的充电速度，故可假设故障期间整个柔直电网的不平衡功率是个定值ΔP［19］，式（5）可进一步化为：

在传统NLM 策略的作用下，直流电压由N个子模块电压支撑，故进一步得到不平衡能量引起直流电压抬升的过程如式（7）所示。

式中：Ceq为整个柔直电网的等效电容；Ud(t)为t时刻MMC 直流侧电压；Ud(t)为t=0 时MMC 直流侧初始电压。

在不考虑系统受端均发生交流短路故障这种极端情况下，最严重的故障情景即为容量较大的受端换流站MMC4发生近区三相交流短路故障，考虑定直流电压站的调节作用，系统单极回路中的不平衡功率约为1 300 MW。图3 给出该故障情景下，柔直电网的直流电压计算值与仿真值对比。

图3 理论计算与仿真直流电压对比Fig.3 Comparison between theoretical calculation and simulation of DC voltage

将表2 的参数代入式（7）中得到：在故障发生后75 ms时，直流电压就会越过650 kV（1.3 p.u.），导致柔直电网闭锁，与图2所示的仿真结果（72 ms）十分接近，验证了公式推导的合理性。

表2 换流站仿真参数Tab. 2 Parameters of MMC

3 ANLM策略研究

由式（7）可知，若能增大换流站子模块电容值或者减少换流站投入子模块数量，就能够抑制因输入输出能量暂时性不平衡而导致的直流过电压。在实际工程中，在故障期间增大子模块电容值难以实现。故本节提出ANLM 策略，在传统NLM 策略的基础上引入了一个自适应限压系数α，将换流站的阀级控制器输出的桥臂单元投入子模块数量乘以系数α，α由限压控制器给出，其取值范围为［0，1］。在受端站发生故障导致直流电压快速上升时，采用附加的限压控制器给出限压系数α来降低同一时刻换流站投入的子模块数量，增大换流站的等效电容值，限制直流电压的同时，也充分挖掘了换流站的储能潜力。

3.1 限压控制器设计

设m端柔直电网中有n端换流站采用ANLM 策略，此时，柔直电网的等效电容值计算如式（8）所示。

式中：Ceq(t)为t时刻整个柔直电网的等效电容；α为限压系数，由限压控制器给出。

设t=0时刻故障发生，t=tA时刻，子模块数量开始自适应减少以限制柔直电网的直流电压，t=tB时刻故障恢复或不平衡功率被切除，子模块数量开始逐渐恢复，t=tC时刻子模块数量恢复至额定值。

在0—tC内，直流电压均满足式（9）。

式中：ΔP为0—tC内柔直电网的不平衡功率；Ceq(0)为t=0 时刻柔直电网的等效电容。为使直流电压在tA—tC期间被限制在AUd（0）附近，Ceq（t）需要满足式（10）。

式中A为直流电压目标值与稳态值的比值。

联立式（6）和式（7），式（10）可化为：

进而得到，若要直流电压tA—tC期间被限制在AUd（0）附近，限压系数α需要满足：

式中：B（t）=UC（t）/UC（0），可由式（6）和式（9）联立求得。

特别地，当m=n，k1=1，k2=0时，有：

由式（15）可知，当柔直电网内各换流站均采用ANLM 策略时，只要求限压系数α能自适应于柔直电网子模块电容电压平均值的变化，直流电压就会被限制在目标值附近。且此时可认为故障期间柔直电网的子模块电容电压都近似等于Ud（t）/αN，这使得限压控制器的设计更为方便。

基于上述分析，柔直电网中各换流站均采用ANLM 策略时，ANLM 策略的实现方式如图4所示。

图4 ANLM策略的实现方式Fig.4 Realization method of ANLM strategy

图4中：系数KG的大小取决于子模块数量自适应变化期间直流电压的目标值，受端交流故障期间，柔直电网需要通过增大受端站的有功电流分量以提高功率送出能力，故直流电压目标值的选取应大于直流电压稳态值，且应低于直流电压的安全界限值。

由式（1）可知，在ANLM 策略限制直流电压期间，只要健全站交流电压目标值在0~A区间，换流站输出的调制比就不会越限，依旧在可调制范围内，不会影响健全站交流侧运行安全。

3.2 子模块数量恢复过程分析

tB时刻，不平衡功率被清除，子模块电容储能开始逐渐释放，各换流站子模块投入数量逐渐恢复。在tB—tC内，整个柔直电网的能量变化满足式（16）。

式中：α(tB)为tB时刻的限压控制器输出的限压系数；KG为比例系数，其大小取决于故障期间直流电压的目标值；EN0i为换流站i稳态运行时的储能。

稳态时，由于换流站能量的产生与消耗是个动态平衡的过程，故可认为此时换流站i的储能是一个大小为EN0i的定值。

由式（16）可以看出，子模块数量恢复过程所需时间的长短取决于柔直电网输出输入功率的差值。

3.3 ANLM策略与传统NLM策略的对比分析

在故障期间，若α为1 且保持不变，则直流电压和子模块电容电压的上升趋势保持一致，为了保证直流电压增量不超过最大允许值ΔUdmax，单个子模块电容的储能增量ΔECmax1有如下限制。

式中ΔUdmax为直流电压增量最大允许值。

同时，其还受子模块电容耐压约束ΔECmax2的限制。

式中：ΔUCmax为子模块电容电压增量最大允许值；UC0为子模块电容电压额定值。

故在柔直电网功率不平衡期间，传统NLM 策略下，单个子模块电容的储能增量约束ΔEC如式（19）所示。

但若在故障期间，α可根据子模块电容电压平均值的抬升而自适应变化，将直流电压限制稳定，子模块电容储能只需满足式（18）约束即可。

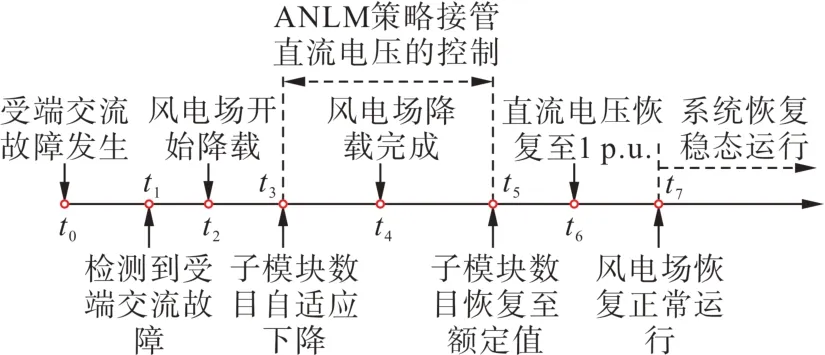
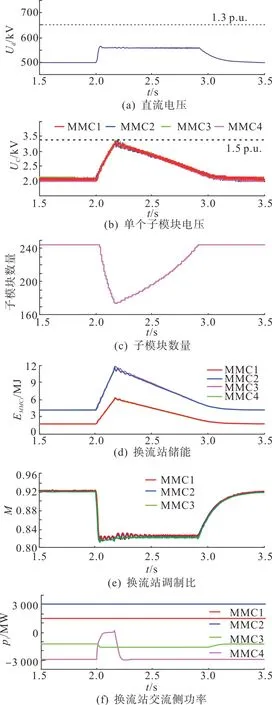
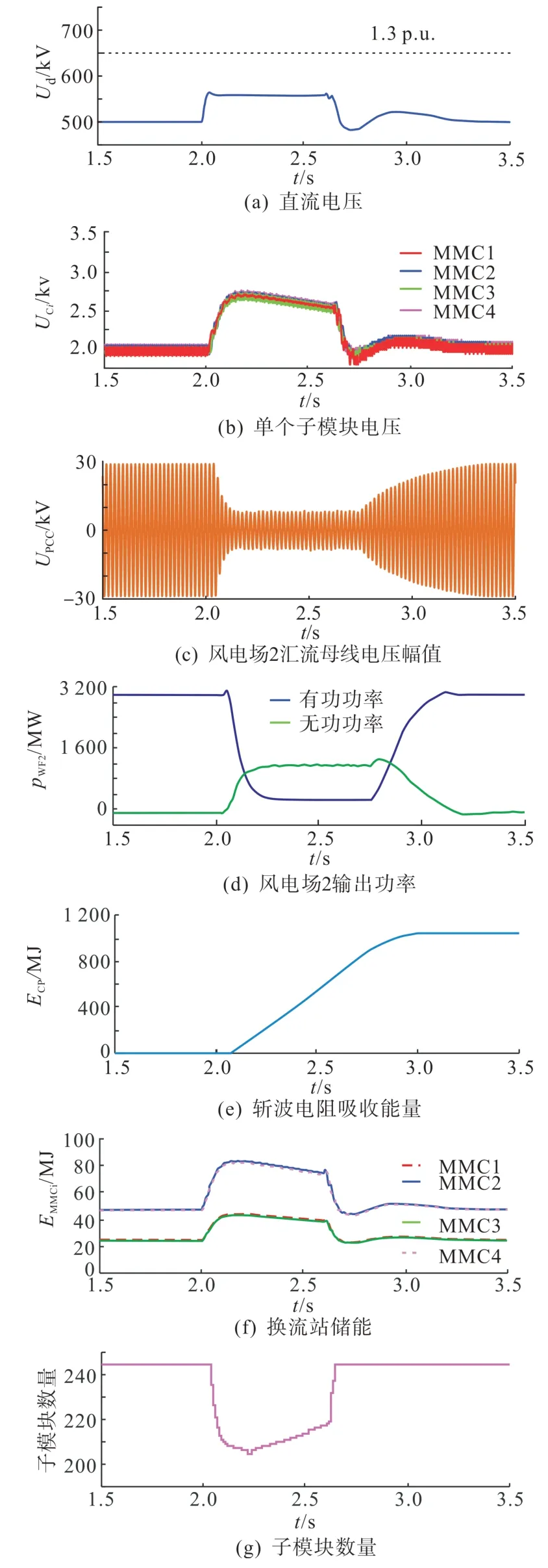
在实际工程中，子模块电容和IGBT 的耐压倍数大于系统直流电压安全界限值，即ΔUdmax

进而得到，ANLM 策略可为系统处理故障争取的最少时间t'表达式如式（21）所示。

式中ΔPmax为故障导致的最大不平衡功率。

综合上述分析，ANLM 策略与传统NLM 策略相比有如下优势。

1） 从能量利用率角度考虑。ANLM 策略在不超出子模块耐压的情况下通过减少各站子模块数量的方式适当地提高子模块电压，充分利用子模块的电压裕度吸纳受端交流故障导致的不平衡能量。在受端恢复正常后，将子模块电容吸纳的不平衡能量平稳地释放到受端电网中，提高了能量的利用效率。

2） 从故障处理时间角度考虑。ANLM 策略为精确投切耗能装置和风电场降载争取了更充裕的时间，提升了系统的故障穿越能力。

直流电压的安全界限值为1.3p.u.，而子模块通常具有2p.u. 的耐压极限［20］，但由于在故障结束瞬间子模块电压会出现较大波动，故将其安全界限值设为1.5p. u. 更为合适。将表2 的参数代入式（20）和（21）中可得到：与传统NLM 策略相比，ANLM 策略使得柔直电网的储能上限提高了约128 MJ，同时可以为系统至少争取约为98 ms 的故障处理时间。即在ANLM策略下，柔直电网的储能上限约为270 MJ，可以实现持续时间不超过170 ms 的任意类型受端交流故障的穿越。

但若受端交流故障持续时间较长，导致子模块因吸纳过多不平衡能量其电压上升至安全边界值，则子模块会被损坏，威胁换流站运行安全，此时所提出的ANLM策略无法单独实现不平衡能量引起直流过电压的故障穿越，需与其他控制策略协同配合才能完成。

4 ANLM 策略与风电机组内部斩波电阻协同配合的受端交流故障穿越策略

4.1 风电场快速降载控制策略

由式（2）可知，通过降低风电场汇流母线电压的d轴分量，就可以实现风电场快速降载。为避免因降压速率过快而导致送端换流站闭锁，工程中多采用交流电压-交流电流双闭环控制结构，附加降交流电压环节的送端换流站控制器设计如图5所示。

图5 附加降交流电压环节的送端换流站控制器Fig.5 With an additional control for AC voltage drop of sendingend converter

图5 中：uWF，abc、iWF，abc分别为风电场汇流母线的电压和电流；uWF，d、uWF，q分别为风电场汇流母线电压的d轴分量和q轴分量；iWF，d，ref、iWF，q，ref、iWF，d、iWF，q分别为风电场汇流母线电流的d轴目标值、q轴目标值、d轴分量及q轴分量；ω为风电场汇流母线电压的角频率；θ为风电场汇流母线电压的相位；L为送端换流站出口处的电感；M、Md、Mq分别为换流站的调制比、调制比的d轴分量和q轴分量，T为一阶低通滤波器的时间常数。

当滞环比较器检测到直流电压快速升高时，控制器判定受端交流故障发生，将通过调低风电场汇流母线的电压目标值来降低风电场馈入至柔直电网的不平衡能量。

uWF，q在送端换流站的控制下接近于0，可近似认为uWF，d为风电场汇流母线电压，按照最严重的故障情景考虑，汇流母线电压需逐渐下降至0.2p.u. 附近才能让风电场不再向柔直电网馈入不平衡能量。在汇流母线电压下降过程中，为了让电压快速跟踪目标值，iWF，d的绝对值会一直增加，但是由于内环电流限幅环节的存在，最终|iWF，d|=iSE，max，其中iSE，max为送端换流站的限流幅值，风电场汇流母线电压的变化近似满足式（22）。

式中：uWF为风电场母线电压；CWF为风电场聚合在风电场汇流母线上的等效电容；iWF，d0为稳态时风电场出口电流的d轴分量。

当风电场满载运行时，iWF，d0为1 p.u.。换流站通常拥有1.1 倍的过负荷运行能力，即iSE，max为1.1 p.u.。

因此可得风电场汇流母线电压变化0.8p.u. 所需时间计算如式（23）所示。

式中ub和ib分别为风电场汇流母线电压与电流的基准值。

取电压和电流的基准值如式（24）所示。

式中Sb为风电场的功率基准值。

联立式（23）和式（24），可以计算出满载运行的风电场汇流母线电压变化0.8 p.u. 所需的时间大约为150 ms 左右，考虑30 ms 的控制器延时，汇流母线电压下降至0.2 p.u. 所需时间约为180 ms。

4.2 风电机组的低电压穿越控制

基于PMSG 的大规模风电场内部机组常见结构如图6所示。

图6 永磁直驱风电机组结构Fig.6 Structure of PMSG

风电场中的每个PMSG 都经一个全功率变换器（full power converter， FPC）连接到柔直电网，每个FPC 都由机侧电压源型换流器（machine side VSC，MSVSC）和网侧电压源型换流器（grid side VSC，GSVSC）构成，MSVSC 采用最大功率点跟踪（maximum power point tracking， MPPT）控制，控制目标是希望其作为一个PV 节点，与变桨距控制配合，确保PMSG 输出功率恒定，GSVSC 采用定直流电压控制，稳定FPC 的直流电压的同时也对无功功率进行控制。为保证风电场具备低电压穿越的能力，在每个FPC 的直流线路正负极之间均需装设斩波电阻R。

当风电场汇流母线电压下降至0.9 p. u. 以下时，风电机组进入低电压穿越模式，GSVSC 需运行在无功电流优先的限流控制模式，在整个降压过程中，GSVSC 的无功电流目标值iqref如式（25）所示［21］。

式中：uWF，N为风电场汇流母线电压的额定值；imax为GSVSC可承受的最大电流。

同时，GSVSC 的有功电流目标值idref如式（26）所示。

由式（26）可知，随着风电场汇流母线电压的下降，GSVSC 输出有功将大幅度降低，而期间MSVSC持续汇集电能，因此会有大量的不平衡能量累积在FPC的直流母线上，使得直流母线电压Udc，WT快速升高。此时需要装设在FPC 正负极母线上的斩波电阻投入使用，吸收风电机组内部的不平衡能量，抑制FPC直流过电压，保证风电机组稳定运行。

工程上通过设定FPC 直流母线电压上下阈值的方式控制斩波电阻的投切，设其上限阈值为Udc，WT，max（本文选为1.15 倍的额定直流电压），则斩波电阻R的大小设计如式（27）所示。

式中PWT，max为风电机组可发出的最大功率。

4.3 故障穿越的时序逻辑

通过ANLM策略及风电场降载控制策略的协同配合可以确保在故障穿越的规定时间内系统安全稳定地持续运行，时序逻辑如图7所示。

图7 故障穿越时序逻辑Fig.7 Sequential logic of fault ride-through

设系统发生受端交流故障（t=t0），导致柔直电网的直流电压持续上升，直至送端换流站检测到受端交流故障（t=t1）后，送端换流站将汇流母线电压的目标值设为0.2 p.u.，短暂的控制延迟后，送端换流站配合风电机组内部斩波电阻开始实现风电场降载（t=t2），在风电场降载完成（t=t4）前，风电场持续向柔直电网注入不平衡能量，若不采取措施的话，可能会导致直流过电压，而本文提出的ANLM策略可抑制不平衡能量导致的直流过电压。为避免送端换流站误认为故障已恢复，ANLM 策略接管直流电压控制期间（t3-t5）的目标电压值应大于1.05 p.u.。若在规定时间内受端交流故障恢复，则子模块数量和直流电压会逐渐恢复至额定值（t4—t6），为确保子模块电容储能快速地释放，需要送端换流站控制器中的滞环比较器检测到直流电压恢复至1 p. u. 后，再逐渐升高风电场汇流母线电压的目标值，使风电场恢复正常运行，随后整个系统会逐渐恢复至稳态运行。若在规定时间内受端交流故障未恢复，则送端换流站断开其交流侧断路器，随后风电场会脱网并停止运行。

在所提策略作用的过程中，故障导致的不平衡能量由换流站存储逐渐转由各风电机组内部斩波电阻吸收。为使风电机组具备应对故障风险的能力，每个机组内部均会装设斩波电阻，而ANLM策略也仅利用子模块的电压裕度使得换流站暂时吸纳不平衡能量，因此该策略无需增设额外设备，不增加额外成本。而且斩波电阻是分置在各风电机组中的，其大小通常为2~5 Ω［22-23］，体积很小，与直接配备耗能装置相比，可降低占地成本，同时因为阻值小，也可有效缓解散热压力。

根据柔性直流一次设备的当前研制进展，换流站阀控系统控制子模块投切的时间响应尺度约为180~315 μs［24-25］，足够匹配直流故障过电压的暂态响应，而且斩波电阻的投切也仅依赖风电机组的本地信号，不需要远距离通信，所提策略的可靠性和快速性也满足要求。

5 仿真分析

在PSCAD 中搭建了图1 所示的风电经四端柔直组网系统仿真模型。各站的详细仿真参数见表2，风电场1 和2 分别由750 台和1 500 台额定功率为2 MW 的等值风电机组采用单机倍乘法聚合而成，风电机组结构如图6 所示。为确保仿真精度，本文将仿真步长和控制步长分别设置为25 μs和200 μs。

本节以MMC4发生持续时长不同的近区三相交流短路故障为例，对3 种不同的受端交流故障穿越策略进行了仿真和对比分析。

5.1 仅采用ANLM策略

该仿真工况中柔直电网中各换流站的阀级控制策略均采用ANLM策略，子模块自适应变化期间直流电压的目标值选为1.12 p.u.。设置故障开始时间为t=2.0 s，持续时长为170 ms。仿真结果见图8。

图8 ANLM策略仿真结果Fig.8 Simulation results of adaptive NLM strategy

由图8（a）—（c）可以看出，在故障穿越期间ANLM 策略通过子模块自适应投切的方式将柔直电网的直流电压限制在560 kV（1.12 p. u.）附近。且期间各站子模块电压均不超过3.3 kV（1.5 p. u.），远低于耐压极限，不会被损坏。由图8（d）可以看出，在整个故障过程中，柔直电网依靠换流站持续吸纳了约为268 MJ 的不平衡能量。由图8（e）、（f）可以看出，故障穿越期间健全站的调制比均在可调制范围内，健全站交流侧电压会保持稳定，ANLM策略并不会影响健全交流侧的功率传输。图8 的仿真结果与本文3.3 小节的推论基本一致。但若故障持续时间更长，子模块有被损坏的风险。综上，ANLM 策略通过子模块短时储能可实现短时受端交流故障的穿越，但不能单独实现持续时间较长的受端交流故障穿越。

5.2 仅采用风电场快速降载控制策略

该仿真工况中，MMC2控制器设计如图5所示，各站阀级控制策略均为传统NLM策略。设置故障开始时间为t=2.0 s，持续时长为600 ms，考虑风电场和送端站的控制延迟为30 ms。仿真结果见图9。

图9 风电场降载控制策略仿真结果Fig.9 Simulation results of the power reduction control of wind farm

由图9 可以看出，由于电流环的限制以及控制延时的影响，本文4.1—4.2 节提出的风电场降载控制策略无法在故障初期及时降载。在风电场大幅度降载前，柔直电网仍会持续累积不平衡能量，导致直流电压超过安全阈值650 kV（1.3 p. u.）。因此，4.1—4.2节提出的风电场降载控制不能单独实现系统程度较深地受端交流故障的穿越。

5.3 采用本文所提出的协同配合故障穿越策略

该仿真工况采用4.3 小节提出的协同配合故障穿越策略，MMC2 控制器设计如图5 所示，各换流站的阀级控制策略均采用ANLM策略。故障情景及风电场和送端站的控制延迟与5.2 小节一致。仿真结果见图10。

图10 所提故障穿越策略的仿真结果Fig.10 Simulation result of the proposed fault ride-through strategy

由图10（a）可以看出，在整个故障穿越过程中，所提策略将直流电压限制在650 kV（1.3 p. u.）以下。由图10（d）—（g）可以看出，仅在风电场大幅度降载前，ANLM 策略通过减少子模块数量增大换流站等效电容的方式吸纳柔直电网累积的不平衡能量，为风电场降载争取时间。2.20 s 后，不平衡能量基本由风机内部的斩波电阻吸收，风电场不再向柔直电网馈入不平衡能量。

对比图10（b）和图8（b）可以看出，所提协同配合策略中，故障期间各站的子模块电容电压峰值较低，且故障结束后，子模块释能由风电场2 和MMC3 共同调节，子模块电压快速恢复至额定值，与单独采用ANLM策略相比，所提协同配合穿越策略对子模块电容的耐压要求较低。

图11给出了图10（c）与图9（c）、图10（d）与图9（d）的仿真对比图。

图11 仿真结果对比Fig.11 Comparison of simulation results

由图11 可以看出，ANLM 策略虽略微影响风电场汇流母线电压的波形质量，但未影响其幅值，因此ANLM 策略几乎未对本文4.1—4.2 节提出的风电场降载控制效果产生影响。

综上，本文4.3 节所提出的协同配合穿越策略能够实现持续时间长、故障程度深地受端交流故障的穿越，能够满足大多数工况下受端交流故障的穿越要求。

6 结论

本文从能量平衡的角度详细分析了风电经柔直组网系统受端交流故障下直流过电压机理，得到故障期间直流电压的表达式，得出结论如下。

提出了可以实现直流电压紧急限制的ANLM策略，采用ANLM 策略的换流站有着更高的储能上限，能为系统处理故障争取更充裕的时间，提高系统故障穿越的能力。

提出了ANLM策略与风电机组内部斩波电阻协同配合的受端交流故障穿越策略。所提策略能够满足大多数工况下受端交流故障穿越的要求，同时该策略不依赖于远距离通信，其可靠性取决于原风电经柔直组网统的控保系统，没有引入额外的不可靠因素，且该穿越策略不需要增设额外的设备，充分利用换流站的储能潜力和风电机组的自身响应，能够减少故障穿越的成本。