计及用户响应度的电动汽车充放电优化调度策略
2023-09-21李军梁嘉诚刘克天韩伟梁宵李鑫
李军,梁嘉诚,刘克天,韩伟,梁宵,李鑫
(1. 南京工程学院电力工程学院,南京 211167;2. 国网江苏省电力有限公司淮安供电分公司,江苏 淮安 223001)
0 引言
截至2021年底,全国电动汽车(electric vehicles,EV)保有量达到784 万辆,其中纯电动汽车保有量640 万辆,占新能源汽车总量的81.63%[1],随着“双碳”政策的推行,能够实现“电能替代”的EV 数量将会得到快速增长。EV 作为一种新型的电力负荷,其充电行为具有随机性强、波动性大的特点。大规模EV 并网时,将会影响电网安全稳定运行。因此,有必要通过合理的手段引导EV 进行有序地充电放电,在一定程度上减少对电网造成的负担[2-4],进而实现削峰填谷[5]、促进新能源消纳[4]、减少系统电压偏差和网损[7]等目标。
有关EV 有序充放电控制策略主要可以分为控制性策略和引导性策略两种。控制性策略是指通过对充放电策略的制定,直接控制EV的充放电过程,包括充放电开始时间、持续时长、功率大小等参数,实现对EV 充放电全过程的控制。文献[8]提出了充电边界曲线的概念,通过调节边界曲线改变EV 的充放电状态,实现对各时刻EV 集群充电容量需求的控制。文献[9]基于可控系数的概念建立EV迟滞控制模型,缓解其无序充电造成的负荷尖峰上升的问题。文献[10]基于TOPSIS 排序算法,根据能够反映EV 充电行为特征的3 个指标,对EV 的充电需求进行量化分析,形成EV 充电需求优先级。文献[11-13]提出了分层控制的策略对电动汽车的充放电调度进行优化。但这类研究在控制过程中往往忽略对用户参与积极性以及可调度容量的评估,在实际应用过程中,随着EV 规模的逐渐扩大,研究可能与实际结果存在一定的差距。
进而有部分研究者提出了引导性的控制策略,通过制定合理的充放电价,引导用户的充放电行为并激励用户参与到充放电调度过程中,也需要考虑调度过程中各方收益的平衡。文献[14]在考虑了各电动汽车聚合商(electric vehicles aggregator,EVA)之间相互竞争博弈关系的基础上,通过实时分布式算法求解各EVA 之间的非合作动态博弈模型。文献[15]通过非合作博弈的方式,解决停车场中EV的充电调度问题。文献[16]基于对用户出行规律的分析,提出了一种计及用户满意度的电动汽车动态分时充电电价制定策略,引导 EV 用户转移充电负荷实现削峰填谷。文献[17-20]在分时电价策略下,以系统负荷方差、用户充电成本、电池损耗成本等为目标函数,建立了电动汽车充电的多目标优化调度模型。上述研究主要针对价格补偿机制下的分时电价和动态电价的制定策略展开研究,但在电价制定过程中往往默认用户全部参与调度过程,未能充分考虑用户的响应度对电价制定过程的影响。
文献[21-24]在对EV用户响应特性进行研究的基础上,通过不同的量化方法,提出相应的EV 用户需求响应度模型,并基于模型进行充放电电价制定方面的研究。但上述研究中,通常将用户响应度设为定值或是认为用户响应度仅受充放电电价这一单一因素的影响,但在EV用户实际的响应过程中,响应度不仅受充放电电价的影响,同时与当前时刻车辆自身荷电状态(state of charge,SOC)相关,例如即使当前时段的放电电价很高,但若车辆自身SOC 很低,用户仍不会选择在该时段放电,而会优先考虑在出行前充电电价更低的时段及时充电以满足出行需求。
因此,本文在研究电动汽车用户出行数据的基础上,综合考虑聚合商充放电价和车辆荷电状态(SOC)对电动汽车用户充放电响应度的影响,建立基于韦伯-费希纳定律的电动汽车用户响应度模型,获取各时刻电动汽车集群的响应容量;统筹考虑电网、聚合商以及电动汽车用户的三方收益,以配电网负荷波动最小、用户充电成本最小和聚合商收益最大为目标,采用粒子群优化算法求解该优化问题。
1 电动汽车充电负荷模型
家用电动汽车一般只在早晚高峰时段使用,全天大部分时间处于闲置状态,本文以家用电动车作为研究对象,选取2017 年美国开展的全美家用车辆的调查数据(NHTS2017)作为基础数据,通过函数拟合,EV 的日行驶里程服从对数正态分布,概率密度函数为[25]:
式中:x为电动汽车日行驶里程;μd、σd分别为均值和方差,σd= 0.87、μd= 3.31。
EV 接入电网和离开电网的时间均满足正态分布,其概率密度函数如下[25]。
式中:ta、tl分别为电动汽车接入和离开电网的时间;σa、μa、σl、μl分别为对应的均值和方差,σa= 3.4、μa= 17.6、σl= 3.2、μl= 8.9。
为避免深度充电对电池造成损伤,本文假设所有EV 在离开电网时的期望荷电状态为Sl,Sl< 1。根据每辆EV 的日行驶里程d和行驶效率χ,可以计算出其接入电网时的初始荷电状态Sa为:
式中:χ为EV 每消耗1 kWh 的电能所能行驶的里程,km/kWh;E为EV的电池容量。
2 基于韦伯-费希纳定律的用户响应度建模
在传统的用户响应度模型中,往往将用户的响应度作为确定量来处理,或是将用户响应度与充放电价格相关联。但是在实际响应过程中,用户的响应度不仅受电价的影响,而且与车辆当前荷电状态(SOC)相关。
当电网处于负荷高峰时,电动汽车聚合商可以通过设置更高的充放电价引导用户主动削减髙峰时段的充电负荷,甚至可以作为电源提供一定量的放电功率;当电网处于负荷低谷时,电动汽车聚合商可以通过设置更低的充电电价吸引用户充电,实现削峰填谷,提高电网效率,延缓电网投资,同时降低电动汽车用户的充电成本。电动汽车用户充/放电的响应度主要受充/放电价、电动汽车电池荷电状态(SOC)的影响。充电电价越高/低,用户的充电响应度就越低/高,充电负荷量就越小/大;放电电价越高/低,用户的放电响应度就越高/低,放电量就越大/小;车辆当前时刻的荷电状态(SOC)越高/低,用户的充电响应度越低/高,放电响应度越高/低。
韦伯-费希纳定律是一种表征心理量和物理量之间关系的定律。该定律指出:用户对某项投资或消费价格变动的感受更多取决于其变动的百分比,而非变动的绝对值,并且这一变动需在一定的界限范围内[26]。因此,使用韦伯-费希纳定律表示用户对于充放电价格和SOC的响应程度为:
式中:Qc(g,s)、Qd(g,s)分别为电价为g、车辆SOC 为s时的用户充电和放电响应度;r1、r2、r3、r4为用户响应度系数;c1、c2为用户响应度常数。
本文建立基于韦伯-费希纳定律的电动汽车充放电响应度曲面如图1所示。
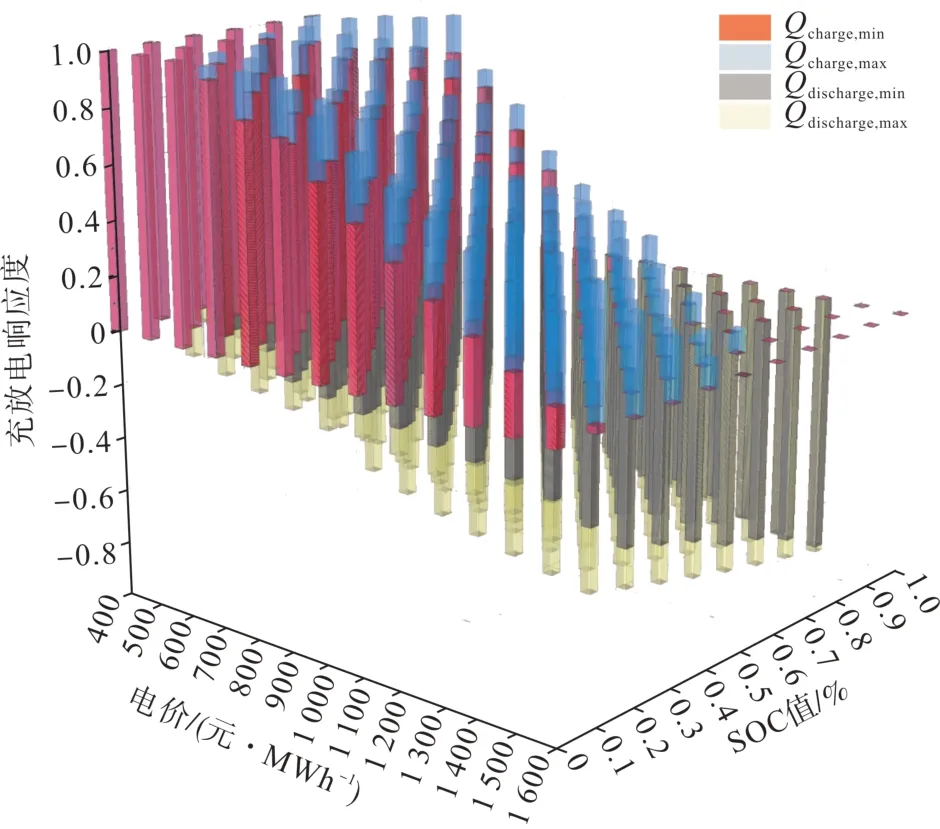
图1 电动汽车充放电响应度曲面Fig. 1 Electric vehicle charging and discharging responsivity curved surface
图1 中,Qcharge,max、Qcharge,min、Qdischarge,max、Qdischarge,min分别为电动汽车参与调度的充响应度上限、充电响应度下限、放电响应度上限、放电响应度下限。
如图1 所示,当某时刻聚合商设定的充电电价为g,车辆荷电状态为s,则EV 用户进行充电响应的比例在Qcharge,max和Qcharge,min之间均匀分布,同理当聚合商设定的放电电价为g,车辆荷电状态为s,则EV 用户进行放电响应的比例也满足Qdischarge,max和Qdischarge,min之间的均匀分布。因此通过EV 接入和离开电网的时间确定各时刻可调度电动汽车的数量,结合所有车辆各时刻的SOC状态和聚合商设定的充放电价求取电动汽车集群实时可充电容量和可放电容量为:
式中:Ec(t)、Ed(t)分别为t时刻充放电价为g时,电动汽车集群实时可充电和可放电容量;N为当前时段可调度电动汽车数量;Pi,c,max、Pi,d,max分别为第i辆电动汽车的最大充电功率和放电功率。
3 计及用户响应度的电动汽车充放电优化模型
3.1 目标函数
为了避免大规模EV 无序充电造成的“峰上加峰”现象并且在一定程度上保证电动汽车聚合商及EV 用户的利益,基于动态电价,以减小负荷峰谷差率、降低EV 用户充电成本和最大化电动汽车聚合商收益为目标,以各时段聚合商向电动汽车用户开设的充放电价和每辆车在每个时间段的充放电功率为优化变量,建立优化调度模型。
1) 使用负荷曲线方差指数来表示一天内电网负荷的波动大小,负荷曲线方差越大,说明负荷波动越大,反之则越小,因此目标函数为:
式中:T为在调度时段数,本文取为24;Pt为t时段叠加电动汽车集群充放电负荷后的系统负荷;-P为系统平均负荷。
2) 基于动态电价,用户参与充放电调度,通过在负荷低谷充电电价较低时充电,在负荷高峰放电电价较高时放电,赚取收益以降低总体充电成本,因此目标函数为:
式中:N为模型中的EV 数量;Pi,c,t、Pi,d,t为t时刻第i辆EV 的充电功率和放电功率;Hi,c,t、Hi,d,t为t时刻第i辆EV 的充电和放电标志位,若为0 则表示EV 当前时刻不充电/放电,若为1则表示EV 当前时刻进行充电/放电;Cc(t)和Cd(t)分别为t时刻聚合商向用户设定的充电和放电电价。
3) EV 聚合商作为中间商通过设定充放电价,提供服务并赚取差价,为满足自身收益要求,以最大化EV聚合商利润为目标函数为:
式中:CG(t)和CCS(t)分别为t时刻聚合商从电网购电的电价和向电网售电的电价。
由于负荷波动、聚合商收益以及用户充电成本的量纲和数量级不同,且聚合商以利润最大为目标,进行归一化处理,并采用线性加权的方法,将多目标优化求解问题转变为单目标问题,为:
式中:F为处理后的目标函数;F1.max为负荷曲线的最大峰谷差的平方;F2.max为用户总充电成本的最大值,通过设定所有车辆均在负荷高峰时段充电且不参与放电求得;F3.max为EV 聚合商利润的最大值,通过设定聚合商购电电价始终保持最低值,售电电价始终保持最高值求得;λ1、λ2、λ3分别为单目标函数F1、F2、F3的权重系数,对于不同利益主体的应用场景,λ1、λ2、λ3可取不同权重系数,本文取λ1=λ2=λ3= 1/3。
3.2 约束条件
1) 可调度容量约束
电动汽车集群的实时充放电调度容量需满足计及用户响应度的可充放电容量约束,具体为:
式中:Ec,EV(t)、Ed,EV(t)分别为t时刻电动汽车集群的充放电调度容量。
2) 离开电网时刻的SOC约束
为保证用户的出行需求,EV 在离开电网时需满足式(12)的约束。
式中:Si,leave为车辆离开时刻的荷电状态;Si,exp为车辆离开电网时的期望荷电状态。为了使电池保持良好的性能,满足用户的出行需求,同时避免频繁的深度充电对于电池的损伤,本文取为0.9。
3) 调度过程的SOC约束
在调度过程中,每辆电动汽车在下一时段的荷电状态需满足式(13),同时为避免深度充放电对电池造成额外损伤,在所有时刻每辆电动汽车的荷电状态需满足式(14)。
式中:Si,t为t时刻电动汽车i的荷电状态;Smin、Smax分别为电动汽车荷电状态(SOC)的下限和上限。
4) 充放电状态约束
为避免EV 在某一时刻同时执行充电和放电的调度指令,需满足式(15)。
5) 充放电电价约束
考虑聚合商的运营成本及用户的承受能力,聚合商设定的充放电价的上下限为:
3.3 模型求解
粒子群算法(particle swarm optimization,PSO)由于结构简单,参数设置较少,收敛速度快等特点,被广泛运用到各个领域。
设粒子群中粒子的总数为popsize= 30,粒子的维数为M,最大迭代次数为itermax= 100,粒子i在第k次迭代时的位置和速度可以表示为xi,k、vi,k。
式中:xiM,k,viM,k分别为粒子i在第k次迭代时在第M维的位置和速度。
每次迭代过程中,所有粒子通过追踪自身的局部最优解pbi,k和全局最优解gbi,k的方式,在搜索空间中寻找最优解。
式中:xim,k为第k次迭代时粒子i在第m维的位置;vim,k为第k次迭代时粒子i在第m维的速度;w为惯性权重,取为0.8,c1、c2称为学习因子,本文均取为2;r1和r2为[0,1]之间均匀分布的随机数;pbim,k粒子i在第k次迭代时在第m维的局部最优位置;gbim,k为粒子i在第k次迭代时在第m维的全局最优位置。
本文以1 h 为时间尺度,将全天分为24 个可调度时段,则粒子位置和速度的维数可表示为:
式中:NEV为参与调度的电动汽车数量;V为每个时段的决策变量数量。
决策变量可具体表示为:[Pi,d,t,Pi,c,t,Pt,Si,t,Hi,d,t,Hi,c,t,Cc(t),Cd(t)](22)求解流程如图2所示。
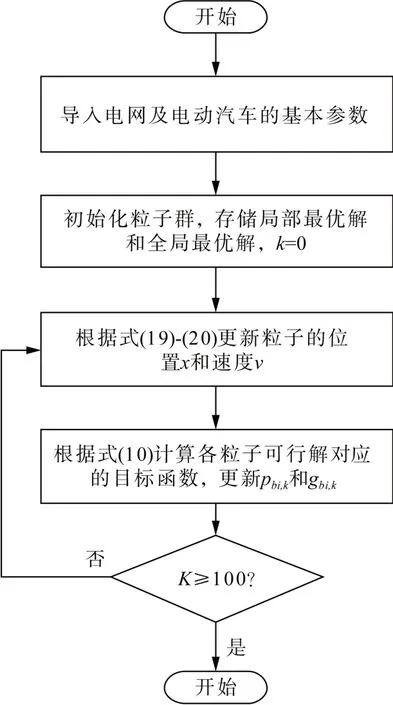
图2 PSO算法流程图Fig. 2 Flow chart of PSO algorithm
4 算例分析
4.1 参数设定
以某一地区的配电网为例,该地区基础负荷采用文献[27]中的数据,配电网选用S13 型变压器,额定容量为1 250 kVA,假设该区域内可参与调度的EV数量为200辆,具体相关参数如表1所示。

表1 电动汽车参数Tab. 1 Electric vehicle parameters
聚合商从电网购电价格和向电网售电价格采用表2给出的分时电价。
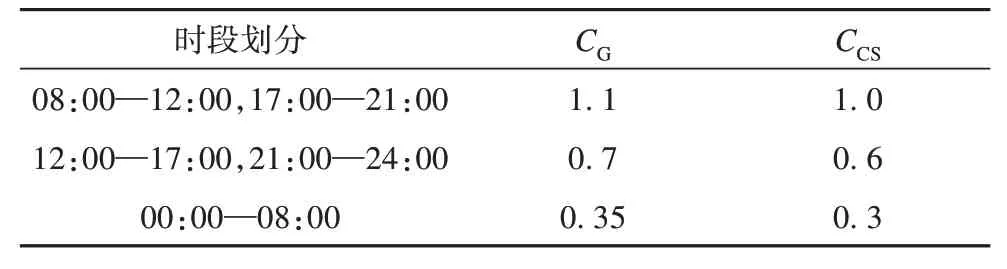
表2 聚合商购售电电价Tab. 2 Purchase and sell electricity prices of aggregators元/kWh
基于已知的聚合商购电和售电电价,算例中假定当充电最高电价为1 600元/MWh,车辆荷电状态SOC 值为0.5 时,充电响应上界中有用户开始响应,而响应度下界中当SOC 值为0.1 时才有用户开始响应;当充电电价为1 100元/MWh,车辆荷电状态SOC 值为0.5时,充电响应上界中有35%的用户响应,充电响应下界中有10%的用户响应;充电电价降至400 元/MWh 时,若SOC 值位于[0,0.4]之间,充电响应上界和下界中的所有用户均参与响应。设最低放电电价为500 元/MWh,即充电电价为电池损耗成本和平均充电成本之和,当SOC值为0.3 时,放电响应下界有用户开始响应,放电响应上界中有15%用户响应放电;当放电电价上涨至900 元/MWh,SOC 值为0.5 时,放电响应下界有50%的用户响应,放电响应上界中有75%的用户参与调度;当放电电价上涨至最高1 100 元/MWh,SOC 值为1 时,几乎所有用户均参与放电响应。因此,聚合商设定的充放电价格、车辆自身荷电状态(SOC)与用户充放电响应度之间的关系仿真结果如图3—4所示。
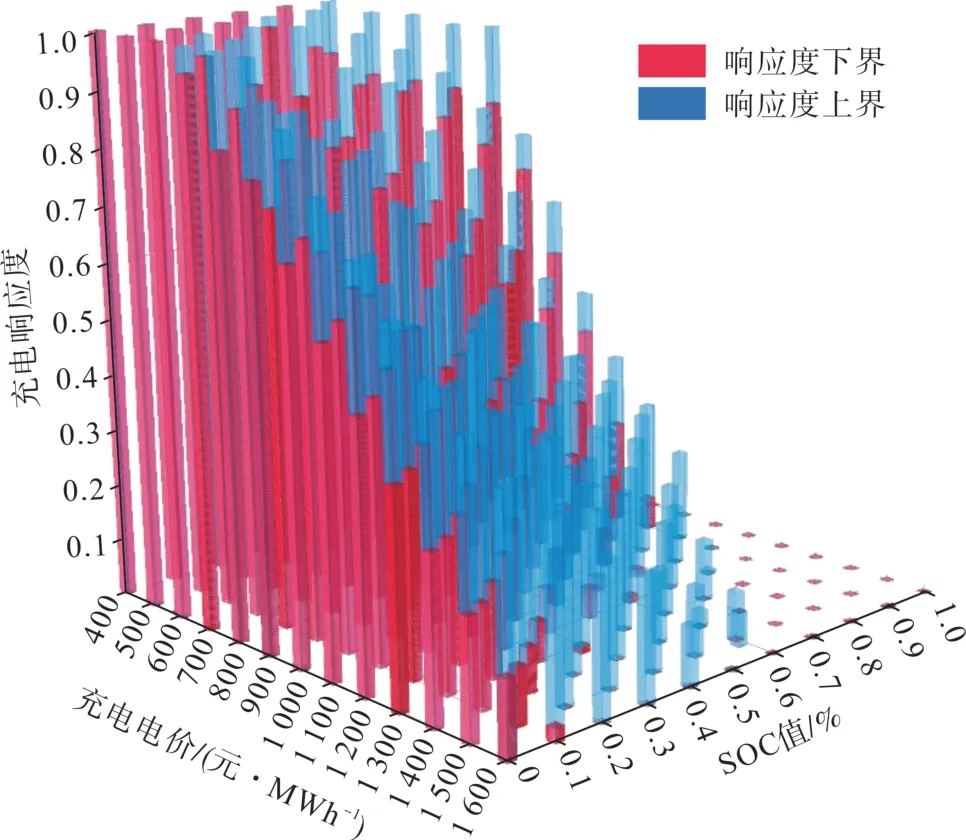
图3 用户充电响应度曲面Fig. 3 User charging responsiveness curved surface
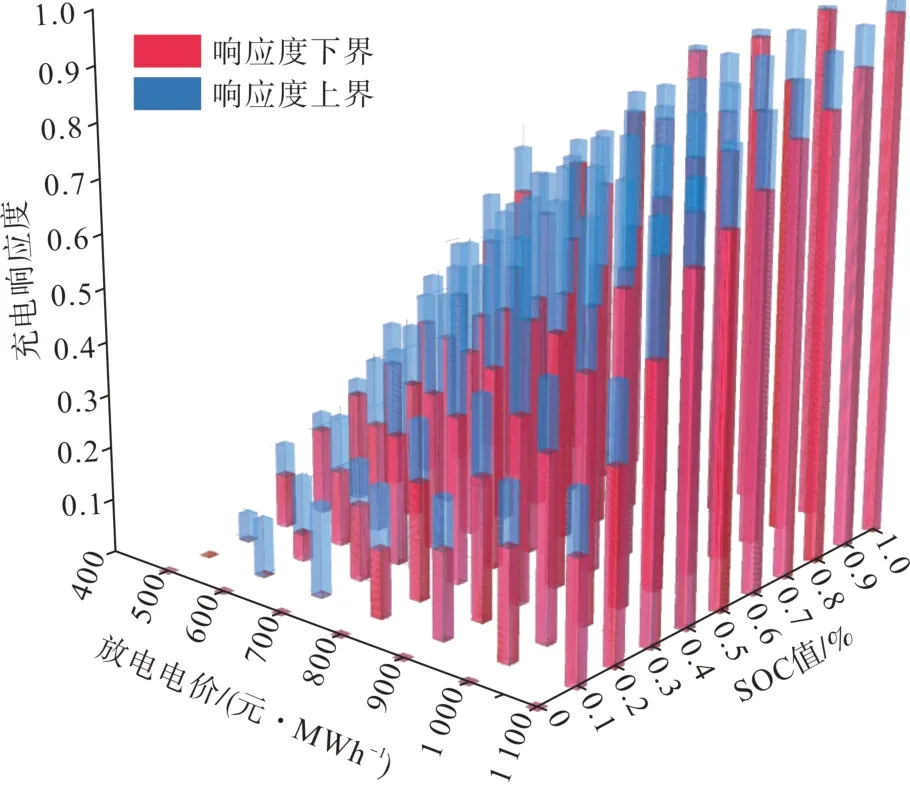
图4 用户放电响应度曲面Fig. 4 User discharging responsiveness curved surface
如图3—4 所示,相同的充放电价和SOC 情况下,用户对充放电具有不同的响应度,但用户对于参与充放电调度进行充电和放电的响应都有较为明显的上下限,且充电响应度都随着充电电价的增加而减小,放电响应度都随着放电电价的增加而增大。
4.2 动态电价下的有序充放电仿真
采用动态电价,选择100 辆EV 进行充放电调度,通过PSO 算法对模型求解,无序充电、有序充电和有序充放电模式下的结果如图5所示。
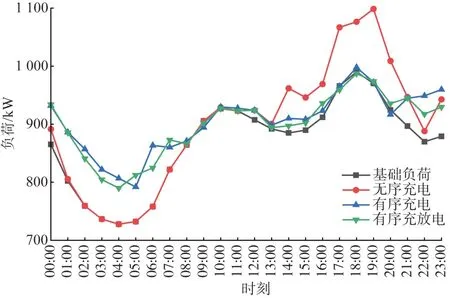
图5 不同充放电策略下的负荷曲线Fig.5 Load curves under different charging and discharging strategies
1) 无序充电:EV 不参与充放电调度,即认为EV 从接入电网时刻起就以最大充电功率充电,直到达到期望荷电状态后停止充电;
2) 有序充电:用户只参与充电调度,即认为用户在任何时刻的放电响应度均为0,EV 在满足充电响应度约束的条件下,以既定的目标函数参与充电调度;
3) 有序充放电:用户参与充放电调度,即认为EV 在满足充放电响应度约束的条件下,以既定的目标函数参与充放电调度。
由图5 可以看出:无序充电策略下,电动汽车集中在17:00—20:00 时结束当天行程接入电网,电网的负荷高峰时段往往会出现“峰上加峰”的现象,变压器存在过载的风险;有序充电策略下,更多的电动汽车用户选择在21:00 时之后开始充电,虽然能够避免负荷高峰对电网的冲击,但会在22:00—23:00时形成了新的负荷尖峰;有序充放电策略下,部分电动汽车用户选择在电网负荷高峰时段(17:00—19:00时)向电网反向送电,以降低负荷高峰,负荷曲线更加光滑。
动态分时电价下分别选择 50、100、200 辆EV进行有序充放电调度,仿真结果如图6所示。
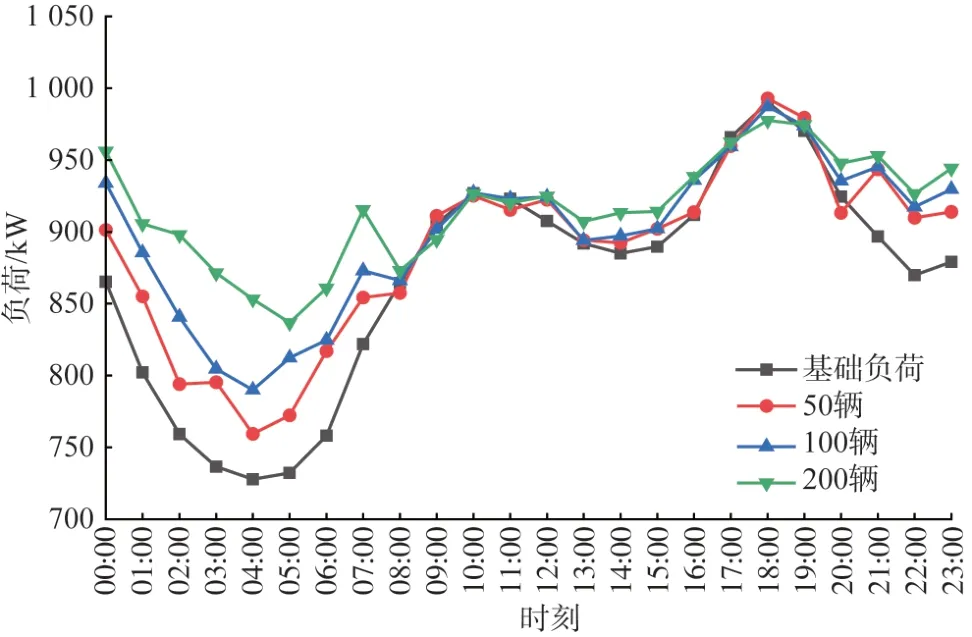
图6 不同EV数量下的负荷曲线Fig.6 Load curves under different EV numbers
由图6可以看出:EV 具有“源-荷”切换的特性,可以起到了削峰填谷的作用。在负荷高峰18:00时,50 辆EV 场景下,负荷曲线高于基础负荷曲线,有部分电动汽车用户因为出行需求选择充电,而在100 辆和200 辆EV 场景下,负荷曲线均低于基础负荷,有更多的用户在此时选择放电以平衡充电成本,随着EV数量的增加“削峰”的效果更加显著;与之相反,在夜间负荷低谷时段,100 和200 辆EV场景下的负荷曲线明显高于50 辆EV 时的负荷曲线,“填谷”效果更佳显著。
综合以上,得出不同充放电策略及不同EV 数量场景下的负荷峰谷差、用户平均充电成本、聚合商收益如表3所示。
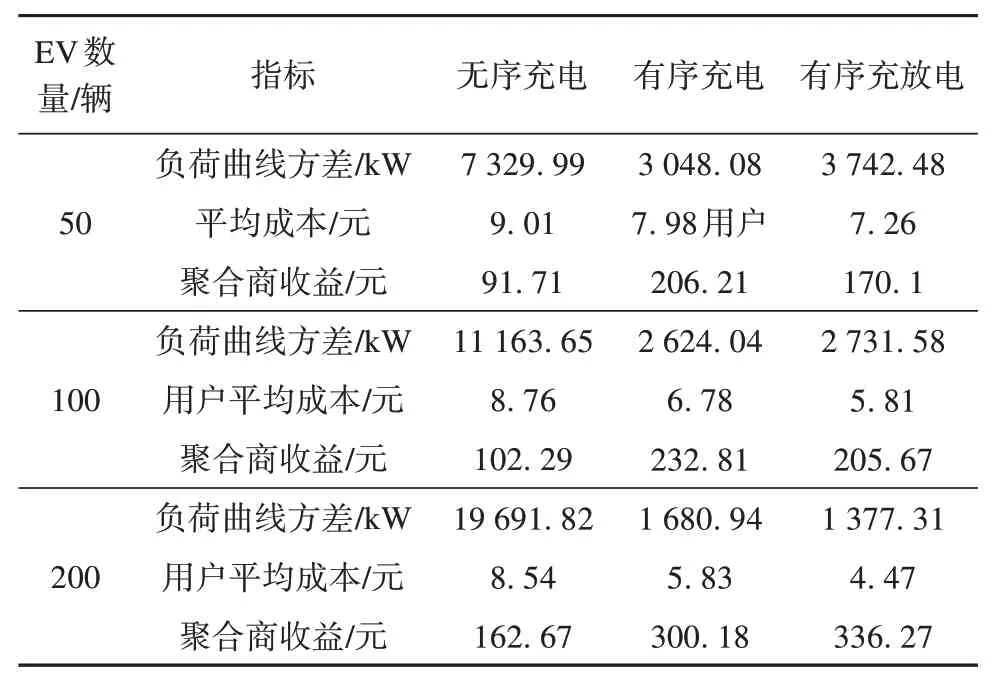
表3 不同策略不同EV数量下的试验指标Tab.3 Test indicators under different strategies and different EV numbers
如表3 所示,在无序充电策略下,随着参与调度EV 数量的增加,系统负荷曲线方差增大,大多数用户在负荷高峰时段接入电网充电,造成峰上加峰的现象,电动汽车用户的平均充电成本也不会随着参与调度EV 数量的增加而明显降低,聚合商的收益难以保证。相较而言在有序充电和有序充放电策略下,以50 辆EV 场景为例,负荷曲线方差分别减少了58.42%和48.94%,用户平均充电成本分别降低了11.43%和19.42%,聚合商收益分别提高了124.85%和85.47%,满足电网、用户和聚合商三方的期望。纵向对比,在有序充电和有序充放电策略下,随着参与调度EV 数量的增加,负荷曲线更加平滑,用户平均充电成本降低的同时,聚合商的日收益逐渐提高,由此可见随着EV 规模的持续扩大,这类调度模式能够有效引导EV的充放电行为,具有良好的应用前景。
图7 为实时电价背景下聚合商的充放电电价曲线,在所有调度时刻聚合商的充电电价始终高于其从电网购电的价格,同理其放电电价也始终低于其向电网售电的价格,聚合商通过在早晚负荷高峰时段设置较高的放电电价,引导用户在此期间向电网反向送电,并在夜晚负荷较低时设置较低的充电电价,引导用户在此期间充电,降低负荷曲线峰谷差,通过电动汽车用户频繁的充放电行为获取服务差价;用户通过类似“低买高卖”的方式,在低谷时段充电高峰时段放电,降低总体充电成本。
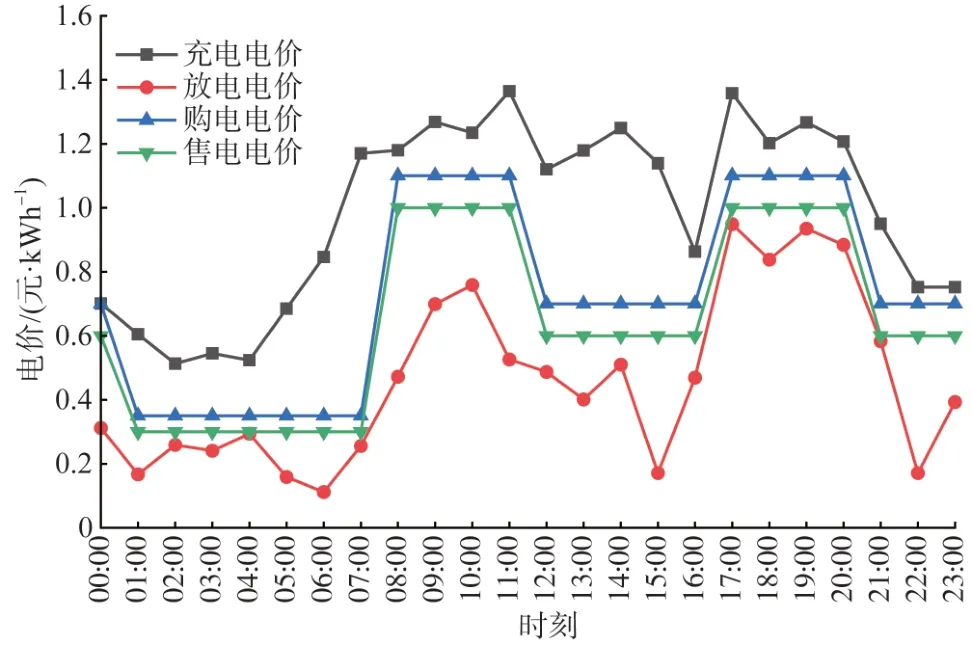
图7 聚合商实时电价曲线Fig.7 Real-time electricity price curves of the aggregator
4.3 分时电价下的有序充放电仿真
在实际调度过程中,车辆的荷电状态(SOC)会随充放电过程发生变化,伴随着充放电价格的实时变化,会导致用户响应度的频繁波动,在一定程度上会降低用户参与充放电调度的积极性,因此,在动态电价的基础上提出了一种分时电价策略,参考当前电网峰谷平电价的制定机制,将全天分为5 个时段,在每个时段内分别保持充电和放电价格的一致,避免用户积极性降低的情况。
基于分时电价,选择100 辆EV 进行有序充放电调度,通过PSO 算法得到优化后的聚合商电价曲线如图8所示。
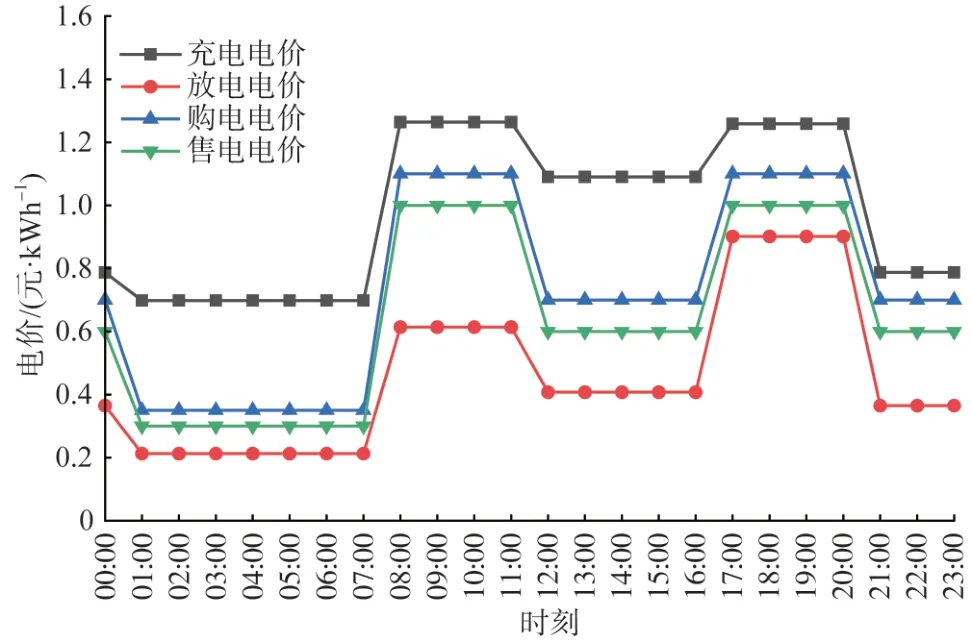
图8 聚合商分时电价曲线Fig.8 Segmented electricity price curves of the aggregator
由图8 可以看出:采用分时电价定价策略,充电电价在峰谷时段的价差小于动态电价场景,用户对于在负荷高峰期参与充电的价格灵敏度降低,进而影响削峰填谷的效果;高峰时段的放电电价依旧高于其在低谷时段的充电电价,保证用户参与充放电调度能有效降低其平均充电成本。
表4 为两种电价定价策略下的实验指标,在分时电价的定价策略下,负荷曲线方差增加了19.06%,由于在既定时间段内的充电电价相同,在低电价时间段的开始时刻往往形成新的充电负荷尖峰,从而增大负荷曲线方差,用户的平均充电成本与动态电价策略相比增加了7.60%,聚合商的收益增加了8.65%,可见采用分时电价策略在保证用户参与积极性的情况下,可以在一定程度上提高聚合商的收益。
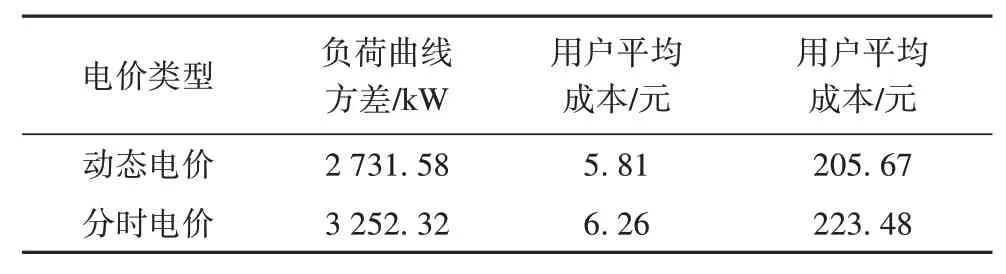
表4 两种电价定价策略下的试验指标Tab.4 Test indicators under two electricity pricing strategies
5 结论
本文通过对用户充放电响应度的分析,考虑聚合商设定的充放电电价、车辆自身SOC对用户参与充放电过程的影响,提出了一种充放电调度策略,以某一地区配电网为案例做仿真分析,得到以下结论。
1) 本文提出的计及用户响应度的电动汽车充放电优化调度策略能够在减小系统负荷波动的同时,降低用户的每日平均充电成本,提高聚合商的收益。
2) 随着参与调度EV 数量增加,本文所提的调度策略能使负荷曲线更为平滑,用户充电成本更低,聚合商收益更高,具有良好的应用前景。
3) 与采用分时电价相比,采用动态电价可以得到更好的调度效果,但其频繁变化的电价会影响用户参与调度的积极性,也会对EV 电池造成额外损伤,在定价过程中需要做出取舍。
在本文研究的基础上,可以考虑电网、电动汽车用户与聚合商不同利益主体之间的博弈模型,进而为研究聚合商参与电力市场报价提供基础。
