基于自适应熵权法的建材装备集团分布式制造资源配置

2023-09-20郭晨,梁爽

数字制造科学 2023年3期

郭晨,梁爽

(1.武汉理工大学安全科学与应急管理学院,湖北武汉 430070,2.湖北省数字制造重点实验室,湖北武汉 430070)

随着工业互联网与智能制造等技术的发展及实践,建材装备制造、汽车制造等传统大型设备制造业呈现出新的特点,包括信息化、智能化、敏捷化等,对于全产业链数据的互联互通和智能决策提出了新的要求[1]。因此国内设备制造业行业结构调整,已形成若干以集团领导为主的分布式制造模式设备制造集团[2]。各集团下属若干子公司之间共享生产、物流资源,子公司同时承接集团总部揽接的生产任务和自主订单[3]。

传统的资源配置研究方向较多关注静态模型、一次性调度中的配置模型和方法优化,如刘晓阳等[4]针对网络化制造问题,引入多色集合理论评估多目标配置策略。Zhang等[5]提出了基于群体进化的制造资源优化配置总体框架,使用灰度分析等建立资源匹配社区。再调度、动态资源配置、自适应等策略逐渐受到关注,如高新勤等[6]采用混合交叉策略对交叉变异概率进行自适应调节,优化算法的稳定性和求解效率。吴书强等[7]提出使用引入了惯性权重机制的鲸鱼优化算法对目标为成本、时间、质量、服务的模型进行求解。Wang等[8]提出一种基于物联网的低碳车间实时调度,将无限次博弈与实时制造数据相结合,改进了现有实时调度。Kim等[9]提出利用贝叶斯算法求解优化问题,自动调整算法的内部参数。上述研究对于解决集团制造模式下的实时资源配置问题做出了许多贡献,但是针对大型设备制造集团的实时调度问题的研究仍有所不足。

笔者基于建材装备集团等大型设备制造企业集团的生产模式离散、需要动态配置、项目周期较长、可靠性要求较高等特点,建立多订单实时资源调度模型,采用引入可靠性因子的自适应熵权机制的配置方法进行优化求解。

1 问题描述及数学模型

1.1 问题描述

因实际运营情况较复杂,做出以下假设:

(1)订单由总公司统一接受、分解成任务再分派给下属生产企业,不考虑自行承接订单的情况。

(2)不考虑总公司和下属企业利益冲突和分配。

(3)需要计算最后交付客户时产生的运输成本。

(4)假设每个下属制造企业同时只承接一个任务。任务一旦开始则无法中断。

1.2 数学模型

考虑到不同的企业地理位置分散,且大型设备制造集团普遍存在生产周期长、参与资源多、边设计边制造、扰动较多等因素,应该主要考虑资源配置方案的成本、工期、可靠性等目标。

目标函数1(成本函数):

(1)

CL(ijmn,i(j+1)uv))

(2)

(3)

CL(ijmn,i(j+1)uv)=Dis(ijmn,i(j+1)uv)/va×

cl(ijmn,i(j+1)uv)

(4)

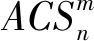
目标函数2(时间函数):

minT=maxTFi

(5)

Dis(ijmn,i(j+1)uv)/va}

(6)

式(5)表示选择最小化最大完工时间TFi作为资源配置的工期目标,式(6)的含义是所有订单中,最后一项任务加工完成时刻TOijmn加上运输到客户指定地点所需时间的最大值。

目标函数3(可靠度函数):

(7)

(8)

上下文中使用的几个决策变量意义为:

(9)

(10)

(11)

(12)

(13)

式(12)、式(13)表示生产资源约束,同一时刻同一资源只能加工一个订单的单个任务,同时同一订单的单个任务只能被单一资源加工。

2 自适应熵权法的两阶段求解

2.1 自适应两阶段模型及实时求解方法

传统实时资源配置问题求解方法中的一种思路是建立任务池,根据一定的触发机制和调度规则实时决定后续的配置方案,可能忽视一定的优化空间。因此可先依据初始订单情况使用NSGA-II(nondominated sorting genetic algorithms-II)算法进行迭代寻优,得到预调度方案,然后在预调度方案的基础上再进行实时调度。

2.2 基于自适应机制的可靠性急迫度与权值

(14)

式(14)为t时刻订单i即所加工任务Oia及所有后置任务的预计平均剩余加工时间等于当前任务开始时未加工任务的预期平均期望加工时间之和。其中Tijmn为任务Oij在下属企业m的资源n上的加工时间。由于生产资源在实际生产中容易遇到扰动,式(15)将历史延期时间和历史产品质量评价加入自适应因子的计算过程。

(15)

(16)

预计物流时间如式(17)所示,表示时刻t时订单预计剩余物流距离,即为运输到当前所选定资源位置、未来所有预计平均物流距离和交货距离之和。另外当j=1时该距离为0;当j=n时,Dist(ijmn,i(j+1)uv)表示最终加工下属企业到交货地点距离。

(17)

(18)

(19)

(20)

2.3 算法流程

该算法分为NSGA-II预调度阶段和实时资源配置阶段。总体流程如图1所示。

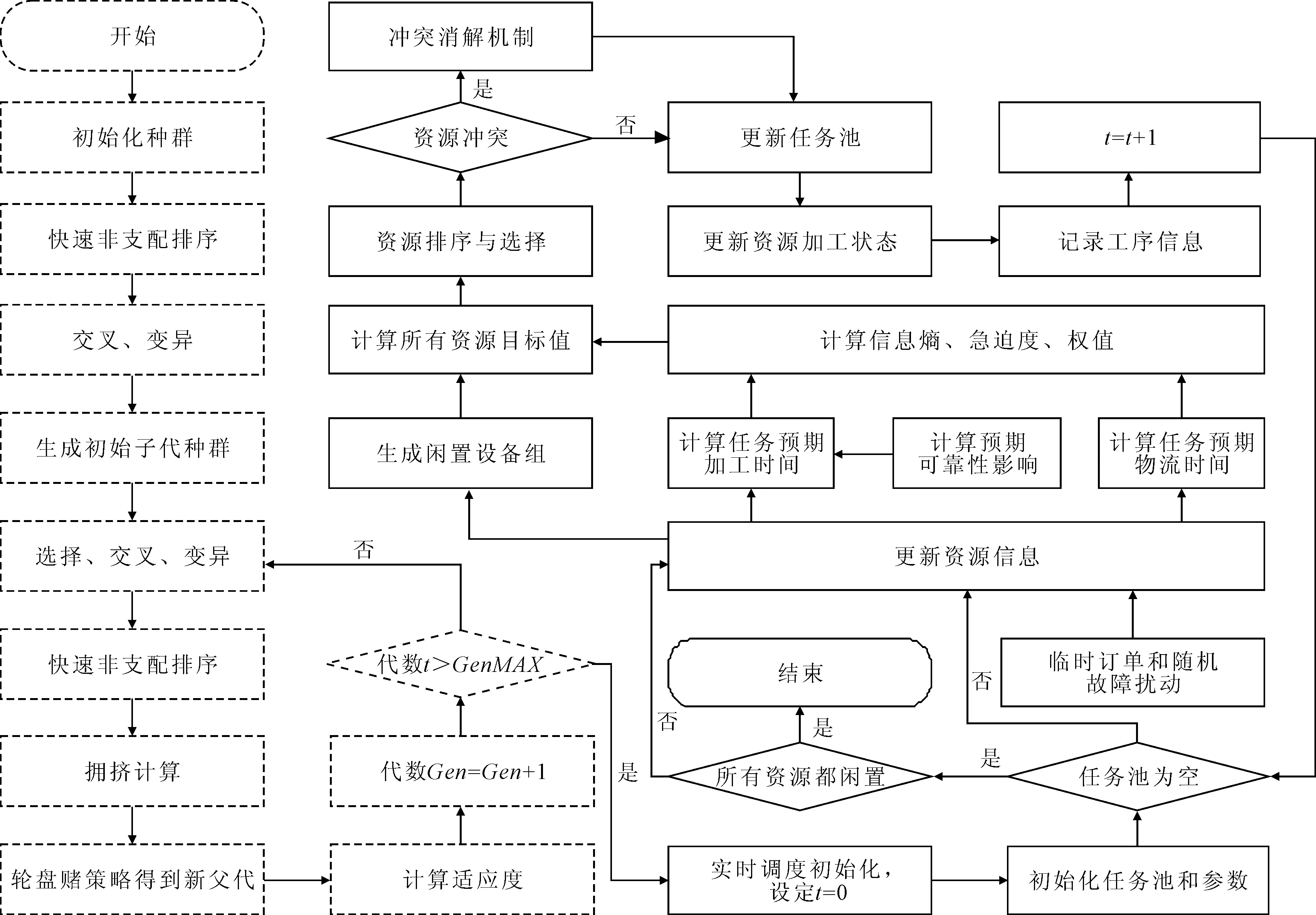
图1 自适应权值两阶段资源配置求解流程

(1)NSGA-II预调度阶段流程如下:

步骤1：初始化种群并计算适应度。

步骤2：对种群进行非支配排序。

步骤3：进化代数+1,通过交叉、遗传、变异得到子代,合并父代子代。

步骤4：对种群进行非支配排序并计算拥挤度。

步骤5：采用轮盘赌策略得到新的父代。

步骤6：检查当前迭代次数是否达到最大代数GenMAX,若达到,则进入实时资源配置阶段,否则进入步骤3。

(2)实时资源配置阶段流程如下:

步骤1：初始化任务池和资源状态,t=0。

步骤2：检查任务池是否为空,若为空则进入步骤7,否则进入步骤3。

步骤3：更新资源信息。

步骤4：计算所有闲置资源与待加工任务匹配时的适应度并排序。

步骤5：按照排序确定最终资源选择,检查是否出现资源冲突现象,若冲突则采用随机分配方式消解,并进入下一步,否则直接进入下一步。

步骤6：返回未得到资源分配的任务到任务池,将已分配任务替换为其后续任务,记录分配结果,使t=t+1,返回步骤2。

步骤7：检查是否所有资源都处于闲置状态,若是则加工完成,否则进入步骤3。

3 实验仿真与分析

3.1 实验设计

以某建材装备生产龙头集团为例进行实验仿真与对比分析。该集团拥有10个下属制造企业,将所有下属制造企业的服务资源封装为30个制造服务单元。每个制造服务单元对各任务的处理速度、成本、历史平均延期比例和历史平均质量评价如表1、表2所示。各下属制造企业之间的距离和物流设备速度、成本各不相同,导致其运输时间各不相同,如表3所示。各订单所属客户、到达时间、交货期限和任务的工作量等如表4所示。

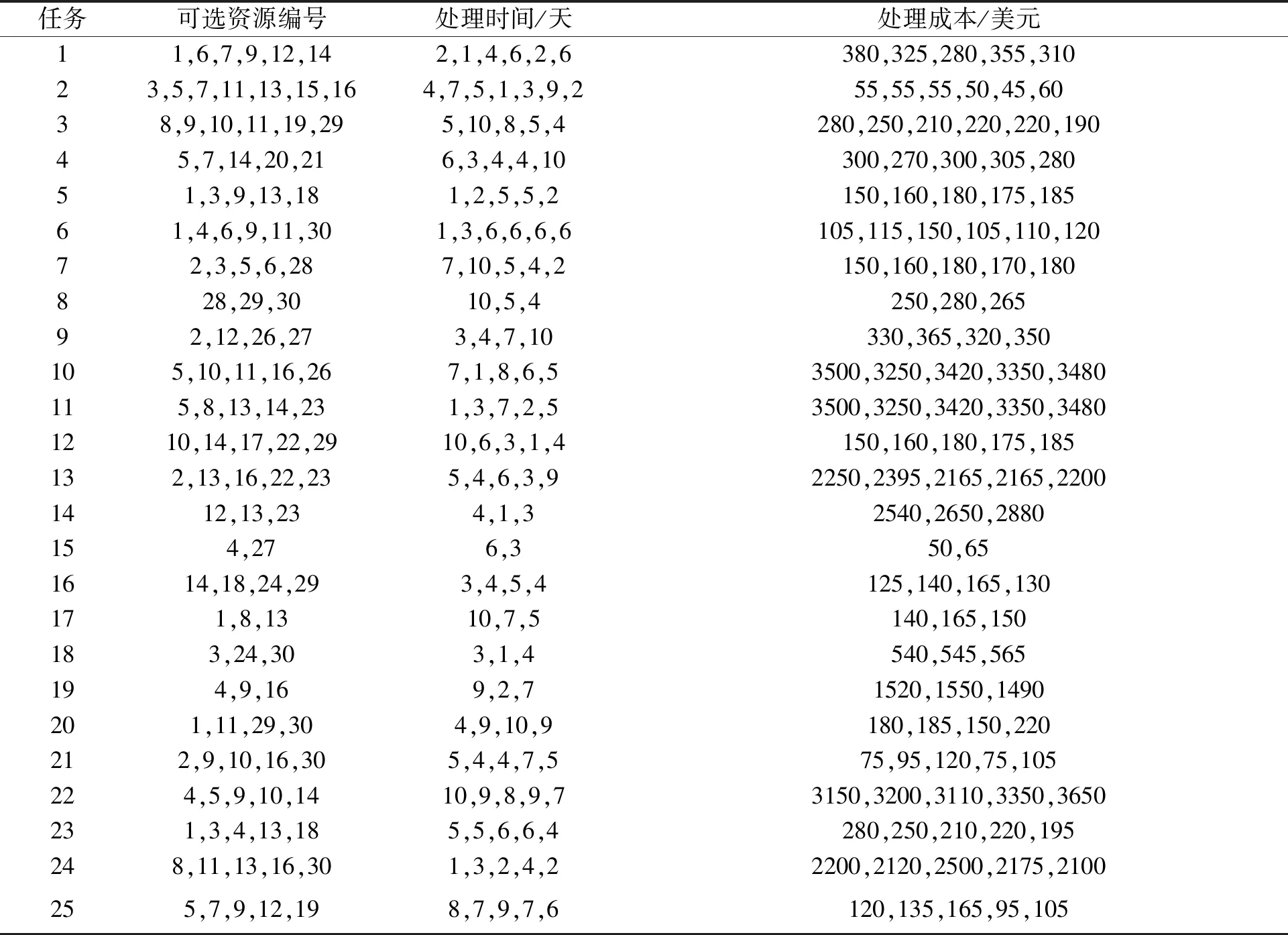
表1 各任务匹配制造资源时处理时间及成本

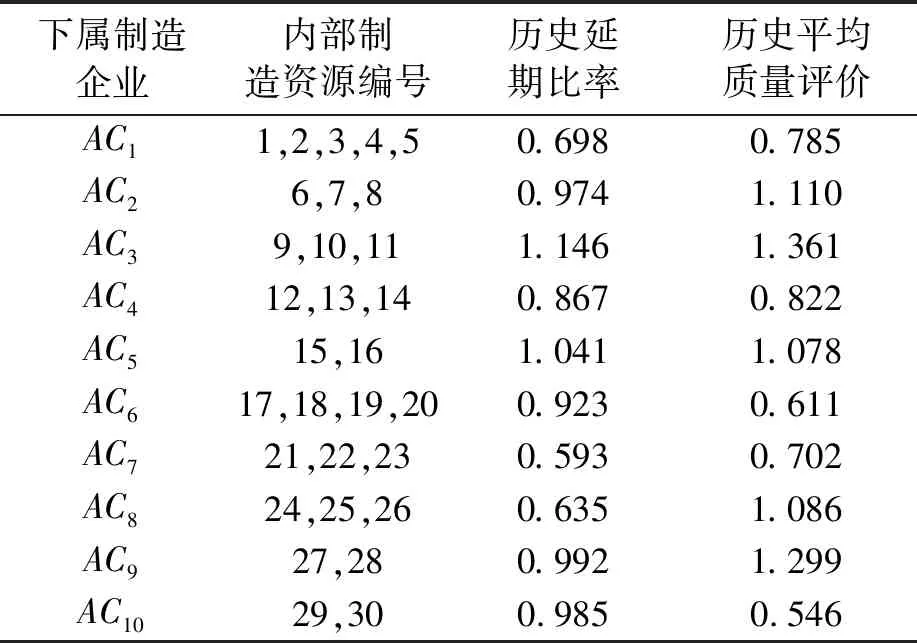
表2 下属制造企业信息

表3 各下属企业之间物流时间天

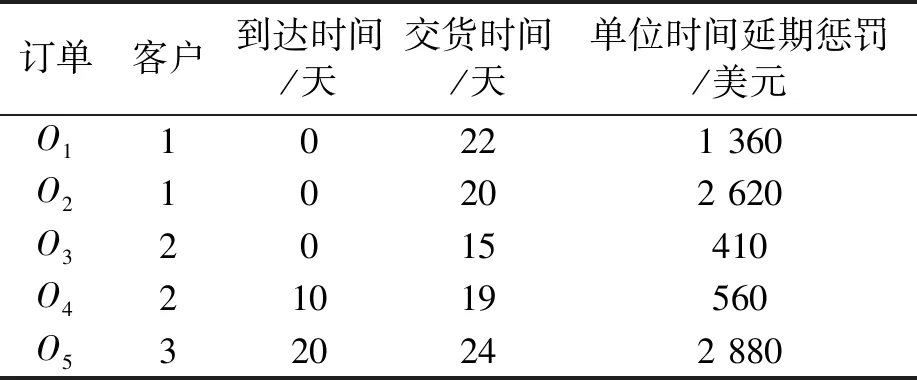
表4 客户订单信息

3.2 实验结果

为了使仿真实验结果具有更强的说明性,将本文中所用配置方法与FIFO(first input first output)、NSGA-II和SCM(slef-adaptive collaboration method)调度算法相对比,结果对比如图2所示。

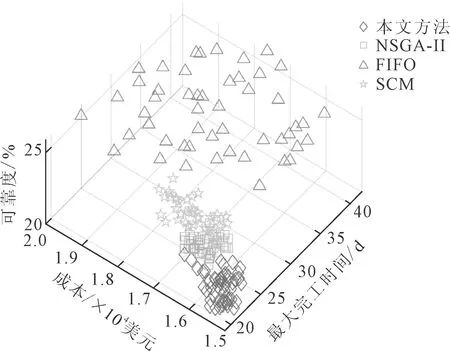
图2 算法结果对比

从图2可知,总体评价中本文所采用的配置方法的总体评价最高,其次是采用NSGA-II算法直接进行资源配置。对于成本函数水平,在不考虑延期惩罚时NSGA-II、SCM和本方法基本持平,FIFO则需要消耗较多的成本。当延期惩罚引入时,SCM和本方法的表现更好。对于时间水平,总体而言时间消耗上本方法

从表5的实验结果可知,由于本配置方法将基于信息熵机制的自适应因子纳入实时配置中,相比于经典调度方法如FIFO等,按期交货的概率获得了较大的提升,同时由于额外将可靠度的影响纳入自适应因子,相比于普通的SCM也能在一定程度上避免故障等扰动对正常生产计划的干扰。相比之下,在不考虑随机扰动或惩罚函数的情况下NSGA-II可以获得更好的结果,但是其抵抗干扰的能力较差。可以认为相比于NSGA-II等传统方法,在大型设备集团制造资源配置过程中本方法更加优越。