立式磁悬浮搅拌器叶频振动控制仿真研究
2023-09-20王海丰
朱 生,陈 圭,王海丰
(温州市博奥机械制造有限公司,浙江 温州 325000)
磁力搅拌器采用同性相斥、异性相吸作用磁场实现无接触磁力传动,能较好地解决生产过程中反应釜的密封问题[1],因此被大量应用于药品、食品、生物医药等领域。目前搅拌器一般使用陶瓷轴承支承转子,设备运行过程中的机械摩擦会产生磨粒[2],污染药品食品。磁悬浮轴承由于具有无接触、无润滑、支承可控可调等特点,在超净环境具有广泛应用前景[3]。
搅拌器作为一种典型的流体机械,在工作时叶轮将会受到周期性的流体反作用力产生流激振动[4],流体力的主频以叶轮叶频为主,这种周期性的外部扰动会传递到转子上,使转子产生较大振动,由于磁悬浮轴承的支承刚度相对机械轴承偏小,若不进行控制可能会导致转子与定子碰摩[5],影响搅拌器的工作稳定性。
国内外学者对磁悬浮转子周期性振动的抑制开展了研究,尤其是针对不平衡振动。Zhou等[6]利用最小均方差算法与影响系数法相结合,对磁悬浮转子的在线不平衡抑制进行了研究。Tiwari等[7]提出了一种基于模型的动态辨识算法,可以同时估计动态参数和不平衡量并进行振动抑制,具有较强鲁棒性。Jiang等[8]提出了一种针对变转速工况下自动提取不平衡质量位置的算法,从而产生相应的控制信号进行抑制。Zhang等[9]设计了一种非线性自适应方法对谐波干扰进行抑制,并在低速下获得了较好的效果。崔培玲等[10]提出了一种通用选择分数阶重复控制方法,可以在任意转速下对谐波振动进行抑制。Gao等[11]在自适应步长最小均方差算法的基础上引入H∞算法,提高系统鲁棒性的同时抑制了不平衡振动。综上所述,目前大部分研究都是针对不平衡振动进行抑制,对于磁悬浮搅拌器来说,其转速并不高,不平衡振动不够突出,而其叶频振动更需关注和控制。
笔者针对立式磁悬浮搅拌器的叶频振动控制进行了研究,首先介绍了磁悬浮搅拌器的支承结构并建立了磁悬浮搅拌器转子动力学模型,然后研究了陷波滤波器并引入相位补偿角来稳定闭环系统,最后搭建控制仿真模型对振动抑制效果进行了分析,验证了叶频振动控制的有效性。
1 磁悬浮搅拌器转子动力学模型建立
立式磁悬浮搅拌器的转子轴系属于长悬臂轴系,同时叶轮处受到的径向力大,故要求转子的径向支承力较大,而叶轮轴向的位移对搅拌器工作影响不大。因此,所研究的立式磁悬浮搅拌器中,径向支承采用主动磁悬浮轴承,轴向支承采用被动永磁轴承。转子的旋转由外部电机和磁力耦合器驱动,为密封设计提供了方便。搅拌器叶轮转子系统结构如图1所示。由于转子在径向4自由度和轴向单自由度的运动可以解耦,而且轴向由被动永磁轴承支承,无需控制,故只考虑叶轮转子在径向4自由度上的运动及振动控制。

图1 立式磁悬浮搅拌器布局示意图
搅拌器整体结构为立式,靠近磁力耦合器端的磁悬浮轴承标记为A端,另一磁悬浮轴承靠近叶轮,标记为B端,叶轮记为C端。以转子质心O为坐标原点建立直角坐标系Oxyz,其中l为A端轴承与B端轴承之间的距离,la、lb、lc分别为A端轴承、B端轴承和叶轮到质心O的距离。A端轴承、B端轴承处转子所受电磁力分解在Ox轴与Oy轴方向上分别为Fax、Fay、Fbx、Fby,C端叶轮所受到的径向力分解为Fcx、Fcy。
由于搅拌器转速一般不高,因此转子可以看作刚性转子。对搅拌器叶轮转子进行受力分析,可得叶轮转子的运动微分方程:
(1)
式中:u=[xa,xb,ya,yb]T为转子位移向量;i=[ixa,ixb,iya,iyb]T为各方向轴向线圈中的控制电流向量;M为质量矩阵;C为阻尼矩阵;Ku为位移刚度矩阵;Ki为电流刚度矩阵;f为外部载荷向量。
各矩阵表达式如下:
(2)
(3)
(4)
(5)
f=[FcxFcylcFcxlcFcy]T
(6)
式中:m为转子质量;Ω为转速;Jp、Jd分别为转子的极转动惯量和直径转动惯量;ki为磁悬浮轴承的电流刚度系数;ku为位移刚度系数。
将式(1)改写为状态空间方程形式:
(7)
式中:f为叶频载荷作用力;O为坐标原点。
搅拌器转子系统的基本参数如表1所示。

表1 搅拌器转子系统基本参数
2 搅拌器叶频振动控制器设计
主动磁悬浮轴承为开环不稳定系统,一般使用PID(proportional integral derivative)控制器使转子稳定悬浮。但磁悬浮搅拌器在搅拌液体时,转子还会受到以叶轮叶频为主频的外部流体力作用,造成转子振动增大,因此还需要额外设计控制器对转子振动进行抑制。实际上搅拌器转子轴系在被搅拌液体内的受力情况非常复杂,但本文不考虑转子轴系所受的外力和弯矩,仅考虑叶轮叶频振动受力。
为了抑制叶轮转子振动,可以用陷波滤波器对周期性的扰动进行滤除,从而使得转子的振动位移减小。因此可以在PID控制器前串联一个陷波滤波器,控制框图如图2所示,其传递函数N0(s)为:

图2 带陷波滤波器的PID控制框图
(8)
式中:ω为叶频,即转速Ω的6倍(由于叶轮有6个叶片组成);λ为调整陷波性能的常数。
由于N0(s)与PID控制器串联,将会改变闭环系统的零极点,会带来稳定性的问题,尤其是在搅拌器工作的低转速工况下。
在转速Ω从0到300 r/min条件下,绘制闭环系统的根轨迹,如图3所示。

图3 闭环系统根轨迹
从图3可知,在搅拌器工作的低转速范围内,复平面的右半平面内存在极点,系统将不稳定。因此引入相位补偿角θ,得到相移陷波滤波器,其传递函数N(s)为:
(9)
由于θ角的存在,系统的相位可以得到补偿,使系统保持稳定。同样在转速Ω从0到300 r/min条件下,绘制含有相位补偿角θ=-100°时,闭环系统的根轨迹如图4所示。

图4 含有相位补偿角θ时的闭环系统根轨迹
从图4可知,由于相位补偿角θ的存在,系统的极点全部移动到左半平面,系统可以保持稳定。
3 搅拌器振动控制数值仿真
为了验证本文算法对叶轮转子振动的控制效果,在MATLAB和Simulink中搭建模型进行仿真分析,如图5所示,模型参数如表1所示。
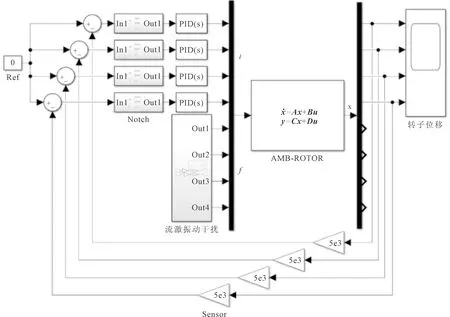
图5 磁悬浮搅拌器仿真模型
设转子转速Ω为100 r/min和300 r/min,则叶轮叶频ω为600 r/min和1 800 r/min,在相移陷波滤波器控制前后绘制转子轨迹如图6和图7所示。

图6 转子转速100 r/min时振动控制前后转子轨迹
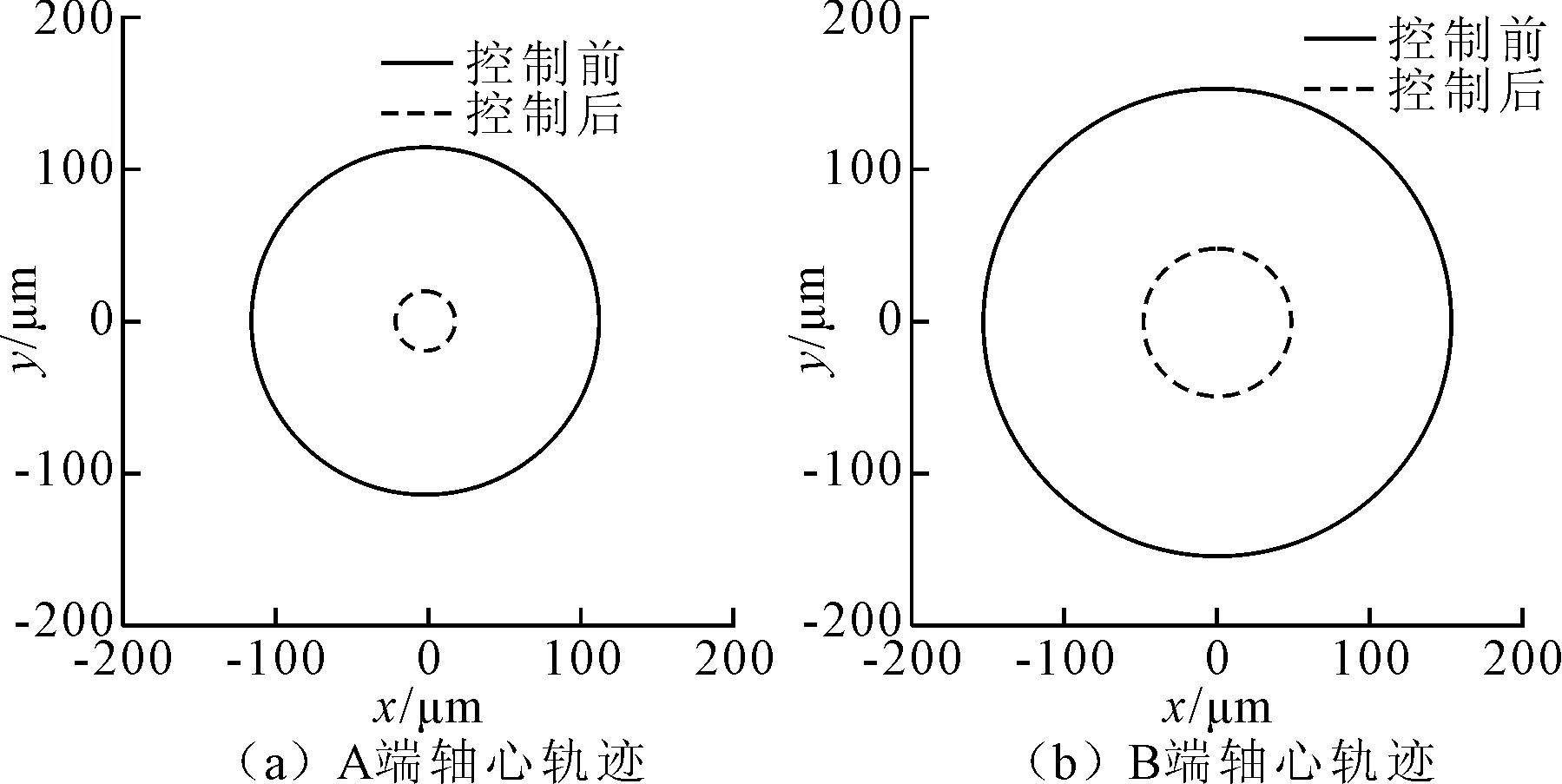
图7 转子转速300 r/min时振动控制前后转子轨迹
从图6和图7可知,由于搅拌器转子轴系为长悬臂轴系,质心落在两个磁悬浮轴承的外侧,因此B端磁悬浮轴承处的轨迹更大。在最高转速300 r/min时,控制前后A、B两端的转子轨迹幅值分别为±113 μm和±153 μm,而在控制后轨迹幅值降低到了±18 μm和±47 μm;转子转速为100 r/min时,振动控制效果更佳,证明了相移陷波滤波器对于叶频振动具有良好的抑制效果。
4 结论
(1)通过转子径向和轴向运动解耦,建立了立式磁悬浮搅拌器4自由度转子动力学模型。
(2)研究了一种相移陷波滤波器叶频振动控制算法,探讨了相位补偿角的有效性。
(3)基于MATLAB和Simulink软件搭建仿真模型,验证所提振动控制算法的效果及有效性。
通过仿真研究初步证明了所提算法的有效性,后续将在对应工况下进行试验研究。此外,由于条件所限,所提出的叶频振动控制未涉及液体的耦合作用力,后续将进一步研究。
