喷漆室空调内部流场分析与结构优化

2023-09-20李泽晨

数字制造科学 2023年3期

吴飞,李泽晨

(武汉理工大学机电工程学院,湖北武汉 430070)

涂装是汽车制造四大工艺之一,由于喷漆室对于作业环境的特殊要求,需要喷漆室空调能够稳定高效的运转。近年来随着涂装工艺设备的发展,对于喷漆室空调的研究逐渐引起学者重视,如对循环风空调系统的建设实现了节能降耗的效果[1-2]。空调系统的优化集中于节能降耗和降低空调运行成本上[3-4],同时针对空调具体的零部件结构进行优化设计[5-6],通过CFD(computational fluid dynamics)的方法对送风状态进行模拟和研究,达到提高流场分布状态的效果[7-8]。目前研究人员对于工业空调系统的研究,主要集中于厂房内部气流组织状态和空调内部的设备如换热器等部件。对于工业现场空调室体内部气流状态的CFD仿真研究较少。

笔者将研究喷漆室空调的结构组成及功能,通过仿真计算对室体内部流场存在的问题进行研究,实验证明仿真方法的可行性,最后提出优化评判指标并进行结构优化设计。

1 空调流场分析与实验验证

1.1 空调模型建立和流场评价指标

以喷漆室循环风空调为研究对象,其布局及结构如图1所示。右侧风机为空调的入风风机,空气由此进入空调室体内,左侧风机为出风风机,将空调处理后的空气送入喷漆室。循环风空调主要组成部件包括:空调室体、供风风机及电机、风管、风阀、表冷器、表热器和温度传感器等。经过对空调室体结构尺寸的实地测量,建立三维模型,其示意图如图2所示。将模型导入到前处理软件ICEM(integrated computer-aided engineering manufacturing)中进行网格划分,最大网格单元尺寸为70 mm,共有网格数量623 344个,网格节点数为583 202,网格正交质量最小值为1,最大横纵比为2,最小角度为85°,整体网格质量(Quality)较好,可以用于后续的流场计算。

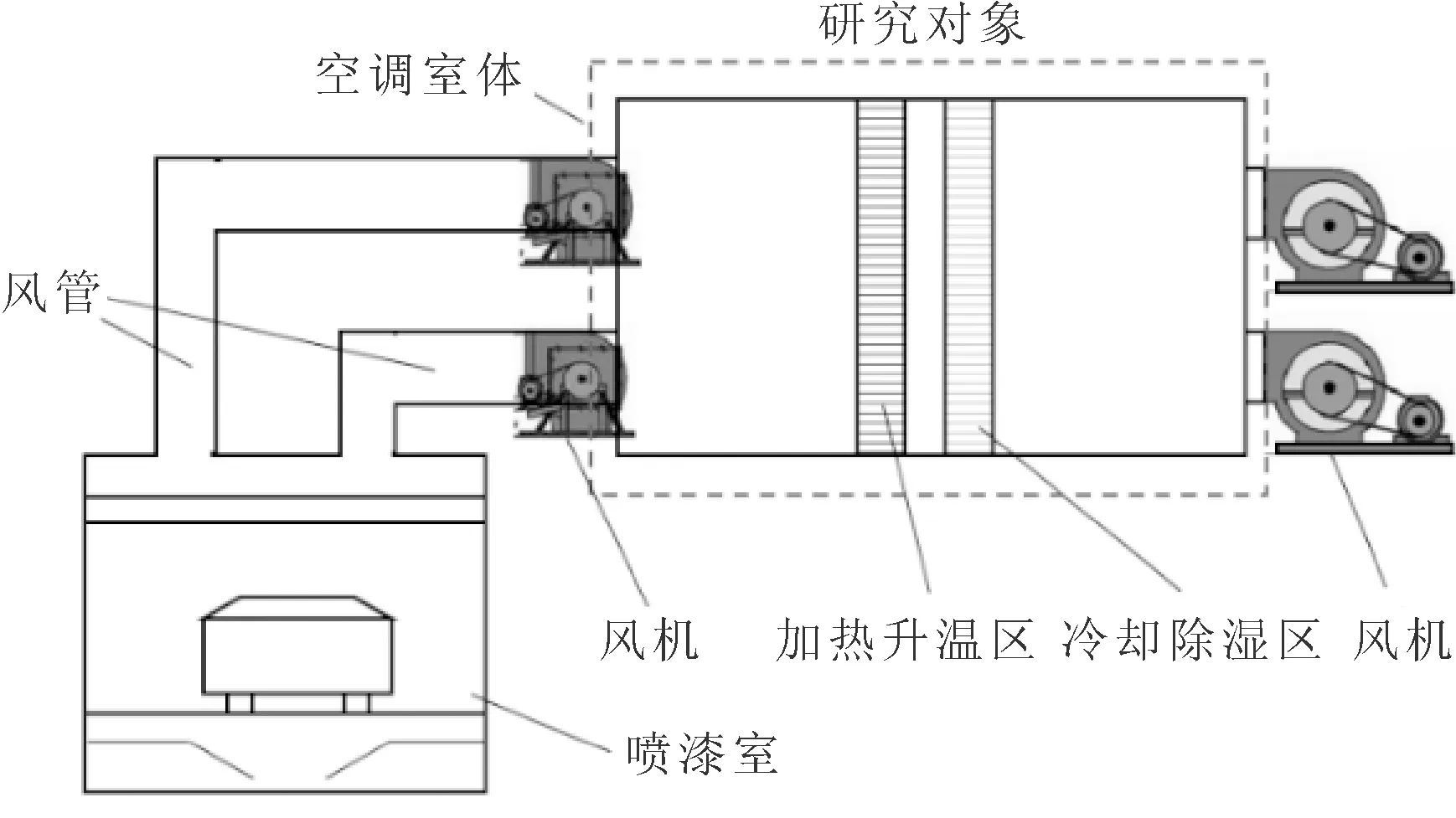
图1 喷漆室循环风空调结构布局

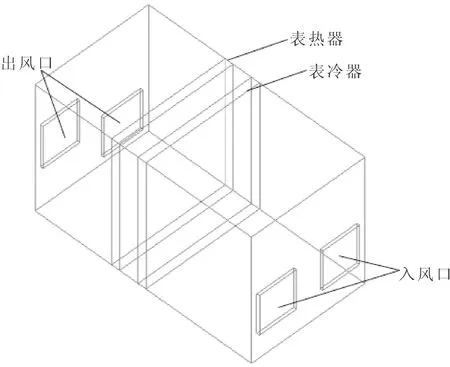
图2 空调室体模型示意图

根据空调室体的结构特点,从温度和速度均匀性角度来梳理相关评价指标,采用的评价方法为相对均方根法[9],其表达式如下:

(1)

将式(1)中温度换为速度,即可表示为速度均匀性指标Uv。当UT越大时表示各测点温度与设定值偏差越大,均匀性程度越差;UT越小时,均匀性程度越好。

1.2 仿真计算与流场分析

使用Fluent软件对流场进行定常模拟,设置入口边界条件,由实测结果可得入口温度为22.8℃,入口速度为8 m/s,其速度方向用矢量表示为(-1,0,0)。湍流模型选择Realizable k-ε双方程模型,近壁面处理方法采用标准壁面函数,模拟计算使用SIMPLEC求解算法,同时启用能量方程和重力选项。表冷器和表热器采用多孔介质模型模拟。

选取具有代表性的截面进行温度和速度云图分析。首先选取合适的分析截面位置如图3所示,选择通过左侧出风口中点的水平截面,入风口和出风口均经过该水平截面。竖直截面也选择通过左侧出风口中点的截面,该截面直接联接出入风口。另外在竖直截面上选择不同高度的4条直线,从低到高依次为y1～y4,在水平截面上选择不同位置的3条直线,按照z坐标由小到大依次定义为z1～z3。将此两个截面和7条直线作为研究对象,分析其流场状态的分布情况。

经过计算得到流场状态的分布结果,空调室体内部竖直截面温度分布云图如图4所示。室体竖直方向的中部位置与室体上下两端温度断层分布。在表冷器与表热器之间的空间内,由于空气经过冷却但尚未加热,故此处为室体内温度最低的区域,温度为22.6℃左右,空气经过表热器加热后达到23.2℃。在空调室体表热器的上部存在局部高温区域,中心温度可达30℃左右。

图4 竖直截面温度分布云图

直线y1～y4温度分布趋势如图5所示。从图5可知,y3与y4曲线的温度比y1与y2的温度高,同时y3与y4存在明显的温度峰值。从图5可以明显看到各条直线上温度分布并不均匀。利用CFD-Post软件在竖直截面上均匀取样点1 000次,求得该截面的平均温度为25.14℃,温度均匀度指标为65.24。

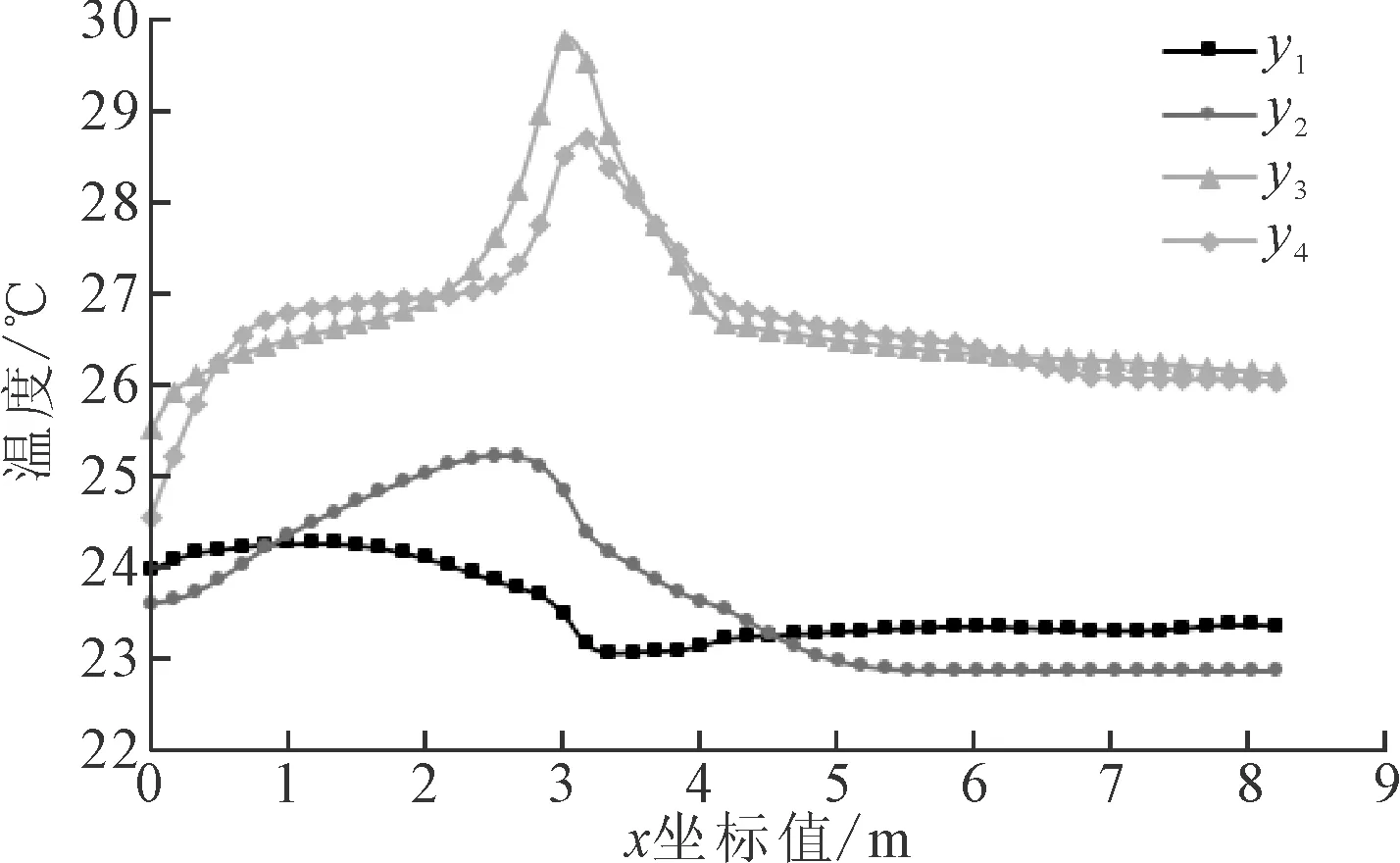
图5 直线y1～y4温度分布趋势图

水平方向的温度云图如图6所示。水平方向上的温度分布均匀性较竖直方向有所改善,大部分区域在23.1℃到25.4℃之间。这是由于两个入风口呈水平方向左右布置,送到空调室体中的主流在水平方向上占较大的比例。两道主流之间的区域温度梯度较大,存在部分温度分布不均匀现象。直线z1～z3温度分布趋势图如图7所示,可以得到不同直线上温度随着x值变化的趋势。经过计算得到该截面内的平均温度为23.44℃,温度均匀度指标为7.72。

图6 水平截面温度分布云图

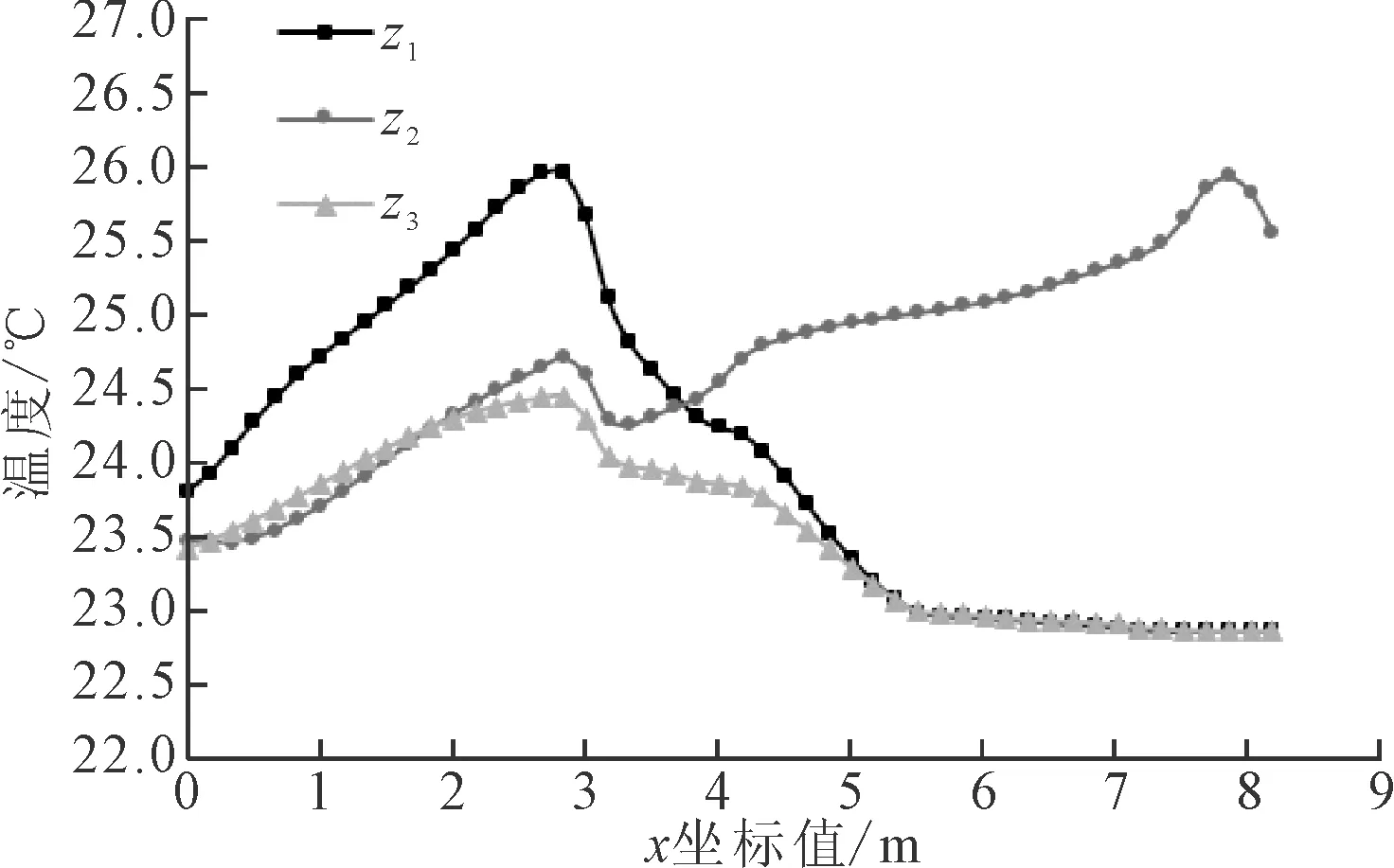
图7 直线z1～z3温度分布趋势图

空调室体内部流场的速度分布状态同样存在不均匀现象,图8为速度分布云图和直线上的速度分布趋势图。速度和温度分布存在明显的关联性:速度大的区域温度较低,速度低的区域则温度偏高。由于空调室体入口和出口直线联通区域附近的空气流速较大,空气并未在表热器充分加热就流出室体,导致空调室体的出风温度较低。

计算得到空调室体内部的各个状态指标值如表1所示,温度和速度均匀度指标存在正相关的关系。水平截面的平均速度最大,且流场均匀性最好。竖直截面由于局部高温区域的存在,其平均温度最高,且流场均匀性较差,整体出口平均温度为24.12℃。

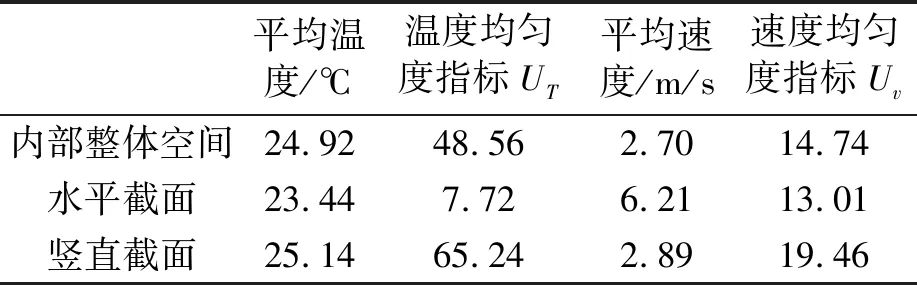
表1 空调室体内部流场状态指标

1.3 仿真结果的实验验证

CFD仿真结果的准确性需要实验测量进行验证,为得到空调室体在整体断面的空气分布状态,采用如图9所示的方式进行测量点布置,测点位置遍布于整个截面,可以全面判断模拟仿真结果的准确性。测量时用探头对各位置逐一测量,由于探头体积较小,可忽略其对流场状态的影响。

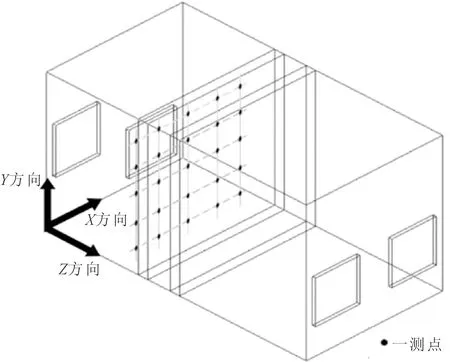
图9 测量点位置示意图

经过测量并记录各点的温度和速度值,其温度曲线如图10所示。仿真值与实测值的变化趋势基本一致,将实测值与仿真计算结果进行对比,计算得到温度场的最大偏差为2.7%,速度场的最大偏差为4.6%,偏差值在5%以内,说明仿真计算结果与实际流场相差较小,证明了仿真结果的准确性,同时说明设定的仿真参数可行。

2 喷漆室空调结构优化

2.1 参数选取与实验设计

采用响应面法拟合出待优化参数与优化目标之间的二阶回归方程,首先选取待优化参数。空调室体的总高度为H,总体长度为L,入风口、出风口距离地面的高度分别为m、n,在优化设计中将保持表冷器与表热器相对位置不变,改变其整体在室体中的位置,其位置用表冷器与入风口之间的距离l表示。各尺寸定义示意图如图11所示。

图11 各尺寸定义示意图

将ε、η和φ作为待优化参数,其定义如式(2)～式(4)所示。

ε=m/H

(2)

η=n/Η

(3)

φ=l/L

(4)

优化设计的目的是提高室体内空气均匀程度,并提高送风温度。空气均匀程度用流场均匀度指标Uv表示,优化目标即为降低流场均匀度指标Uv。考虑到空调入风口与出风口处风管的安装结构,在其上下极限位置分别预留0.2 m的余量,据此极限位置可计算得出ε和η的取值范围为0.042～0.646。由于表冷器与表热器需要进行设备检修,因此其距离入风口(出风口)壁面的距离需要预留宽度不小于1.0 m的空间,由此计算出φ取值范围为0.122～0.720。

使用Design-Expert软件生成每组实验的各个参数值列表,采用BBD(box-behnken design)法进行实验次数和各参数的设定[10]。对每组参数所确定的空调结构重新构建模型,进行CFD计算得到仿真结果。参数值与仿真计算结果如表2所示。

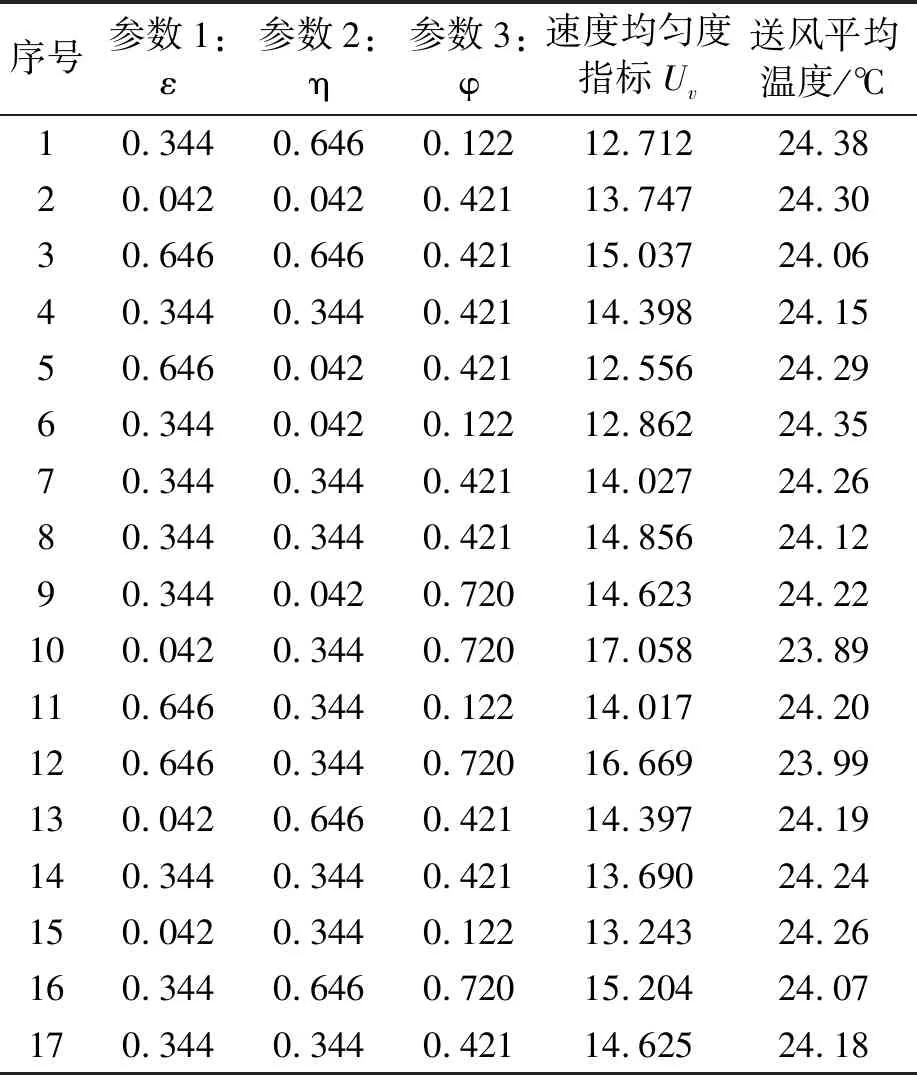
表2 参数设定值与优化结果表

2.2 回归方程的建立与优化模型的求解

采用线性回归模型,进行优化目标Uv与三因素之间回归方程的拟合,得到二阶回归方程:

Uv=12.71-4.25ε+5.61η+0.92φ+5.02εη-

3.22εφ+2.02ηφ+5.55ε2-9.77η2+4.72φ2

(5)

分析响应面图像如图12和图13所示,在参数取值范围内不存在极值点,三维响应面图形呈现马鞍形,无法通过图像判断目标函数为最值时各因素的取值,需要通过软件优化筛选。

图12 三维响应面云图

图13 二维响应面图

通过Design-Expert功能进行优化分析,设置优化目标Uv的优化方向为取极小值,通过计算得到Uv的极小值为12.230,即空调室体内的速度分布最均匀的状态,此时3个因素ε、η和φ的取值分别为0.400、0.042、0.122。由此根据3个因素的定义计算出对应的空调室体结构m、n、l的参数值分别为1.92 m、0.20 m和1.00 m。

重新建立模型并进行仿真验证,计算出均匀度指标和送风平均温度如表3所示,本次优化速度均匀度指标上提高16.8%,出风口温度提高0.23℃,能量利用率有所提高,流场状态得到改善。