基于倾斜阵的距离与方位联合估计

王卓越 张博 李宇

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院先进水下信息技术重点实验室 北京 100190)

(3 中国科学院大学 北京 100049)

0 引言

阵不变量方法是一种利用浅海环境中宽带信号频散效应实现声源定位的方法[1]。与波导不变量相比，阵不变量方法不用形成声强的干涉结构就可以实现对声源距离的估计[2]，具有实时性和鲁棒性，因此，成为国内外关注的热点。

阵不变量方法具有实时稳健的优点，但该方法不能直接应用于宽带连续信号声源的定位问题上，宽带连续信号的多径到达混叠在一起，提取出相互分离的波束到达角难度大，无法实现阵不变量的解算。盲反卷积技术的提出使阵不变量方法成功应用在信号类型未知的声源定位场景中[3]。文献[4]研究了阵列倾斜对该方法定位精度的影响，发现阵列倾斜会严重影响该方法的定位效果；提出了一种自校正算法，用来改善二维平面内由阵列倾斜角度引起的定位精度下降的问题。文献[5]利用未知阵列倾斜角度的倾斜阵列研究了匹配场方法和阵不变量方法的定位效果，发现利用浅海频散效应进行定位的无源定位方法都对阵列倾斜非常敏感，匹配场方法由于不具备对阵列倾斜角度的校正能力，在阵列倾斜且阵列倾角度未知的情况下无法实现有效的定位，阵不变量方法可以利用自校正能力对垂直阵的阵列倾斜进行实时的修正。文献[6]利用倾斜角度已知的阵列研究了倾斜阵匹配场方法的定位效果，发现在阵元与孔径相同的条件下，倾斜阵由于具有等效的水平孔径，定位精度明显优于垂直阵。文献[7]利用螺旋线阵和倾斜阵实现了匹配场方法的三维定位。

在已有的利用倾斜阵阵不变量方法定位的研究中仅分析了声源与阵列倾斜平面共面时的简单情况，对阵列倾斜平面与声源非共面情况下的研究仍非常欠缺。在前人的研究中，自校正算法仅能对声源距离进行估计，无法获得声源的方位信息。针对上述问题，本文在阵不变量的自校正算法的基础上，构建倾斜阵被动定位的三维模型，并提出一种基于倾斜阵的方位距离联合估计算法，算法首先利用倾斜阵给出目标的初步距离估计值，利用代价函数匹配补偿阵列倾角在声源-接收平面的投影量，修正测距误差的同时用过阵列倾角投影量反向估计声源方位，利用倾斜阵同时对声源目标的方位和距离要素进行估计。这种方法的优点是简单易行，具有较好的实时性，利用垂直阵产生的较小倾斜角度实现了声源方位的有效估计，这对垂直阵的声源定位有着重要意义。

1 基本模型

阵不变量方法是一种不需要前向计算模型且具有鲁棒性的被动定位方法。该方法利用平面波波束形成技术获取波束角度和传播时间上相互分离的多径相干到达，从中提取声源的距离信息，已有研究中忽略了声源与倾斜阵存在夹角的复杂情况，仅针对二维平面内的简单模型研究自校正算法的性能。现将该问题扩展到三维模型，本节首先介绍三维空间内倾斜阵基于盲反卷积技术的阵不变量方法。

1.1 倾斜阵定位模型

倾斜阵与声源位置的几何模型如图1 所示。阵列不发生倾斜时，阵列与坐标轴z轴重合，坐标原点O定义为阵列倾斜角度Δθ为0 时阵列延长线与水面的交点。设阵元数为N，阵元间距为d，倾斜阵的中心阵元位于z轴上，坐标为(0,0,zc)，假设阵列在水流流速作用下发生倾斜，阵列倾斜角度为Δθ，θ为阵列的观测角度，观测角度θ以顺时针为正，阵列倾斜角Δθ以逆时针为正。宽带连续声源位于x轴正半轴，其坐标为(x0,0,0)。声源距离rs是声源目标相对于倾斜阵的中心参考阵元的水平距离，声源方位φ从倾斜阵端射方向开始计算，以逆时针方向为正，如图1所示。

将z轴与x轴形成的平面称为“声源-接收平面”，倾斜阵张成的平面与x轴形成的夹角记为声源方位角φ，阵列倾斜角在声源-接收平面内的投影记为ΔΘ，当阵列倾斜角度较小时(如Δθ ＜30°)，ΔΘ满足[4-5]：

阵元n的编号满足n ∈[1,N]，设m=(N+1)/2-n，则倾斜阵第n个阵元的坐标可以表示为

1.2 倾斜阵阵不变量方法

浅海波导中，坐标为rs=(x0,0,0)的点声源辐射一个信号s(t)的傅里叶变换表示为[8]

其中，φs(ω)是声源信号的未知相位分量。此时，倾斜阵第n个阵元接收信号pn(t)的频域信号Pn(ω)为

其中，G(rn,rs,ω)为声源与倾斜阵(1 ≤n≤N)的第n阵元之间时域格林函数g(rn,rs,t)的傅里叶变换。将波束转向特定方向θ提取声源信号，并捕获其相位分量φs(ω)，波束输出的频域表达式为

其中，τn(θ)表示阵元n接收到的来自θ方向入射路径的相对时延，T(θ)为入射角度为θ的多径到达传播到参考阵元的传播时延，利用波束输出的相位消除阵列接收信号Pn(ω)中声源信号的未知相位分量，通过归一化得到频域格林函数的估计值：

其中，声速取c=1500 m/s，在浅水环境中β ≈1，公式(8)可化简为ˆrt=-c/χt。通过波束-时间域的不同到达值解算出倾斜阵阵不变量χt：

2 方位与距离联合估计方法

基于倾斜阵的方位与距离联合估计方法主要由倾斜阵的阵不变量定位方法和三维模型下的自校正方位距离联合估计算法两部分组成。算法首先通过倾斜阵的阵不变量方法对声源距离进行初步估计，初步估计结果通常存在较大的估计误差，利用自校正方位距离联合估计算法修正初步测距结果，得到声源距离估计的精确值。并利用代价函数给出阵列倾角投影量的估计值Δ ˆΘ，结合传感器估计出的阵列倾角Δˆθ，实现对目标方位进行反向求解。图2 为基于倾斜阵的方位与距离联合估计算法流程图。后文中统一简称为“联合估计算法”。

2.1 波束峰值点分段搜索算法

利用倾斜阵波束-时间偏移图中的波束峰值点估计阵不变量，至少需要得到4 组相互独立的波束-时间数据(sinθi,ti)，利用分段峰值搜索的方式找出波束-时间偏移图中的多个峰值点。

从波束随时间的偏移图像上可以总结出规律，一般情况下，每个波束峰值点都在该波束亮点的中央，将半个波束亮点的时间长度记为Δthalf，下面对波束峰值点的分段搜索算法进行简要描述：

第一步：对所有的波束-时间数据进行全局搜索，找出全部波束数据的峰值点记为(sinθ1,t1)，波束峰值点计数值i=2。

第二步：在所有满足t ＞ti+2Δthalf的波束-时间数据中重新搜索峰值点记为(sinθi,ti)，波束峰值点计数值i=i+1。

第三步：重复第二步，直至所有的波束峰值点全部被找出，结束搜索。利用多组波束-时间数据计算阵不变量，根据式(8)对声源目标的距离初步估计。

2.2 自校正方位距离联合估计算法

在文献[4]提出的自校正算法的基础上，本文提出了一种自校正方位距离联合估计算法，改善了文献[4]中自校正算法仅能对声源距离信息进行解算的问题，实现了对声源方位与距离的同步估计。根据图1 所构建的三维模型，自校正方位距离联合估计算法的具体步骤可以描述为

步骤一：在阵列角度搜索范围内选取一个阵列倾角Δθ，并计算调整后的波束角度在声源-接收平面内的投影：

步骤二：采用最小二乘估计方法对修正后波束角度计算阵不变量：

T=[(t1,t2,···,tK)T1T]，1 是1× K维 的向量，1=[1,1,···,1]，波束-时间数据可以利用2.1 节提到的分段搜索方法获得。

步骤三：再利用修正后阵不变量估计值反向求解波束角度投影量：

其中，K是波束偏移图中波束峰值点的个数。

结合式(1)和式(16)，可以推出：

步骤六：利用传感器对阵列倾角Δθ进行估计，假设通过传感器估计出的阵列倾角的无偏估计量为Δˆθ，此时目标的方位的估计值也可以求解：

3 系统仿真与性能分析

本节使用仿真验证联合估计算法的有效性和合理性，预先假设利用传感器估计出的阵列倾角是无偏估计量，在此基础上对联合估计算法性能进行分析。首先通过仿真验证算法的有效性，随后研究阵列倾斜角度对测距精度的影响以及阵列倾斜角度和声源方位对联合估计算法的影响。

3.1 联合估计算法性能验证

使用KRAKEN 对典型浅水环境下倾斜阵的情况进行仿真，浅海波导的参数如图3 所示。采用Pekeries 模型，水深H=100 m，声速cw=1500 m/s，密度ρw=1000 kg/m3，海底介质声速cb=1700 m/s，密度ρb=1900 kg/m3。

图3 典型浅水环境参数Fig.3 Typical shallow water environmental parameters

声源信号采用400～1200 Hz 的宽带连续噪声信号，采样频率为20 kHz，带内信噪比为20 dB。声源坐标为(2000,0,0)，声源到坐标原点O的距离r0为2000 m，接收阵列阵元数为25，阵元间距设为2 m。阵元分布在26～74 m 深度处，倾斜阵的中心参考阵元坐标为(0,0,50)，垂直阵的倾斜角度为5°。声源与倾斜阵平面构成的夹角φ为60°。图4(a)是声源方位角为60°时阵列接收到的格林函数理论值，图4(b)是声源方位角为60°时通过盲反卷积提取到的格林函数图像，图4(c) 是利用图4(b)格林函数得到的波束-时间偏移图像。

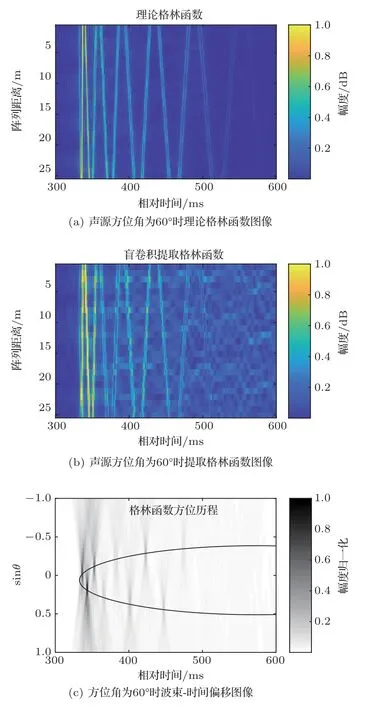
图4 阵列倾斜平面与声源成60°夹角时格林函数图像和波束-时间偏移图Fig.4 Green’s function and beam-time migration diagram when the incline angle between array inclined plane and sound source is 60°

图4(c)前4 个波束峰值点时间分别是337 ms、343 ms、353 ms、423 ms，对应阵列观测角正弦值-0.031、0.164、-0.122、0.306。通过最小二乘方法估计阵不变量χt并解算声源距离。直接利用倾斜阵进行测距的估计结果为2911 m，相对误差为45%。

通过自校正方位距离联合估计算法对阵列倾角在声源-接收平面内的投影值进行估计，估计结果如图5 所示，Δθcosφ的估计值为2.5°，经过算法校正后距离估计值r为2171 m，相对误差降低到8.6%，比校正前减少了36.4%。在已知阵列倾角为Δθ为5°的情况下，求得方位角的估计值ˆφ为60°。由于倾斜阵存在固有的左右舷模糊问题，此处仅考虑声源方位为0°～180°之间的情况。

图5 方位角为60° 时联合自校正算法的代价函数Fig.5 The cost function of self-calibrate algorithm at azimuth angle of 60 degrees

3.2 联合估计算法定位精度影响因素的定量分析

联合估计算法的影响因素主要包括阵列的倾斜程度和声源的方位角，本节首先分析了阵列倾斜角度对测距精度的影响，随后分别研究了阵列倾斜角度和声源方位这两个影响因素对联合估计算法的影响，对比处在不同倾斜角度的阵列估计来自不同方位的声源位置时联合估计算法性能的优劣。

3.2.1 阵列倾斜程度对测距精度影响的定量分析

自校正算法的测距性能仅与阵列倾角有关，本小节主要分析当声源方位角为0°时阵列倾斜程度对测距精度产生的影响，图6 分别是倾斜角度Δθ为0°、1°、3°、5°、10°、20°时倾斜阵接收到的波束-时间偏移图像。图6的各子图中红色的点是波束-时间偏移图中波束峰值点的实际位置，蓝色的点是修正后波束峰值点的位置，黑实线为修正前的拟合曲线(通过红色点拟合出的椭圆曲线)，黑色虚线是修正之后的拟合曲线(通过蓝色点拟合出的椭圆曲线)。可见，随着阵列倾斜角度的增大，修正前的拟合曲线(黑实线)对称轴逐渐偏离sinθ=0，经过自校正算法的校正，拟合曲线(黑虚线)重新回归sinθ=0 这条对称轴。

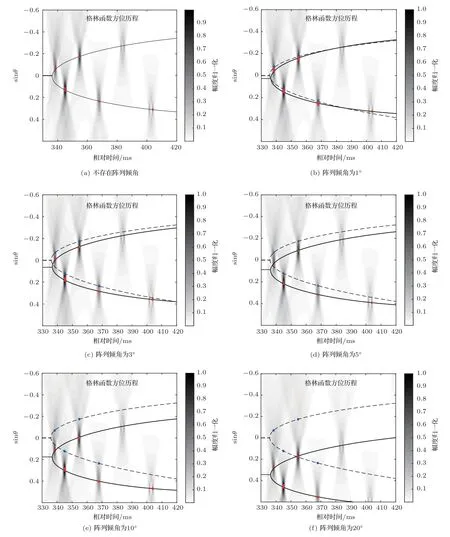
图6 阵列倾斜程度对波束时间偏移图的影响Fig.6 Effect of array tilt on beam-time migration pattern

表1 汇总了不同阵列倾斜角度下校正前后的测距精度。从表1 中结果可以看出，10°以内阵列倾角经过自校正算法处理之后，声源距离估计精度有较为明显的提高，测距相对误差稳定在10%以内。若不对阵列倾角进行修正，随着阵列倾角增大，引起的测距误差也会逐渐增大。当阵列倾角为70°时，测距误差高达90.1%，通过算法修正之后恢复到24.6%。当阵列倾角超过70°时，自校正算法失效。

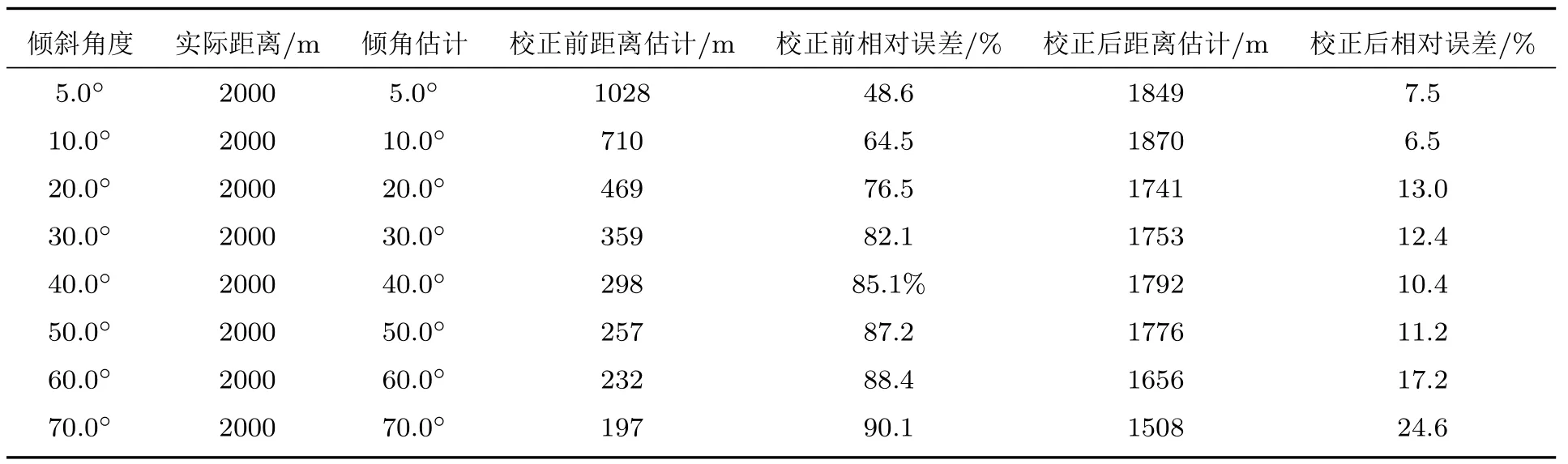
表1 阵列倾斜角度对测距精度的影响Table 1 Influence of tilt angle on ranging accuracy

3.2.2 声源方位对联合估计算法的影响的定量分析

在声源距离为2 km、阵列倾角Δθ为5°的情况下，分析声源位于不同方位角时联合估计算法的精度，结果如表2 所示。当φ处在[30°,80°]区间内，直接利用倾斜阵测距存在较大的估计误差，且无法估计声源的方位。通过自校正方位距离联合估计算法能够使声源距离的相对估计误差稳定在15%以内，方位角的估计误差稳定在3.5°以内，实现了对声源方位的有效估计。当φ处在[0°,30°]和[80°,90°] 区间内时，方位角估计质量显著下降，存在较大误差。

表2 声源方位角对联合估计算法的影响Table 2 Influence of sound source azimuth on joint range and azimuth estimation method

当倾斜阵平面旋转至靠近y轴(即φ ＞80°)或旋转至靠近x轴(即φ ＜30°)时，都会存在方位估计误差较大的问题，特别是在当方位角较小(φ ＜30°)时，方位角的估计精度明显下降，这是由cosφ趋近于1 时方位角φ的分辨率较低导致的。当φ ＞80°时，cosφ趋近于0，阵列倾斜角度在x轴的投影值也趋近0°，方位角的估计精度也随之下降。

图7 分别是方位角为20°、40°、60°、80°时联合估计的结果。由于利用倾斜阵直接测距无法获得声源的方位信息，因此假定目标在倾斜阵的延展平面内。图7 各子图中绿色虚线就是倾斜阵平面与水面xOy平面相交线的延长线，黑色十字代表目标的真实位置，蓝色圆点代表直接用倾斜阵阵不变量方法对目标位置的估计值，红色圆点表示联合估计算法的位置估计值。可以看出联合估计算法能够对不同方位角度目标实现有效的位置估计。

图7 阵列倾斜角度为5° 时方位与距离联合估计结果Fig.7 Joint estimation results of azimuth and range when array tilt angle is 5°

3.2.3 阵列倾斜角度对联合估计算法的影响的定量分析

在声源距离为2000 m、方位角φ为30°的条件下，分析当阵列的倾角不同时联合估计算法的精度。仿真结果如表3 所示。当阵列倾斜角度较小时(如Δθ ＜40°)，方位角的估计误差较小，稳定在2°以内，同时声源距离估计的相对误差稳定在15%以内。随着阵列倾斜角度的不断增加，阵列倾斜角度的投影量ΔΘ逐渐无法满足ΔΘ ≈Δθcosφ的近似表达式，因此当阵列倾角Δθ ＞40°时，自校正方位距离联合估计算法对方位角余弦值cosφ的估计值会存在较大误差，方位估计精度明显下降。当阵列倾斜角度Δθ≥60°时，联合自校正算法无法准确定位，测距精度明显降低，声源方位估计也出现较大偏差。

表3 阵列倾斜角度对联合估计算法的影响Table 3 Influence of tilt angle on joint range and azimuth estimation method

图8 表示的是在不同阵列倾斜角度下联合估计算法的定位效果。根据表3 中多组仿真实验结果和图8 中的定位效果可以得出结论，当阵列倾斜角度在40°以内时，联合估计算法对声源二维平面内的位置都具有较高精度的估计。

图8 声源方位角为30°时方位与距离联合估计结果Fig.8 Joint estimation results of azimuth and range when the source azimuth is 30°

4 结论

在浅海环境下，阵不变量方法的定位精度受到阵列倾斜角度限制，当阵列阵元数一定的情况下，阵列倾斜角度越大，波束时间偏移图中波束峰值点的移动越严重，声源距离的估计误差越大。自校正算法利用波束时间偏移图中波束峰值点随阵列倾角移动的物理规律对阵列倾角进行有效的估计和补偿，改善倾斜阵测距效果不佳的问题。在该文的仿真条件下，自校正算法能够对70°以内的阵列倾角进行有效修正，提高了倾斜阵声源测距的准确性和稳健性。

另外，本文提出了一种基于三维模型的自校正方位距离联合估计算法，结合阵不变量方法实现了对宽带连续信号声源的定位，能够同时获得声源的方位和距离要素，但定位性能受到阵列倾斜角度和声源方位的影响。为此，本文基于简正波理论，利用KRAKEN 仿真分析了阵列倾斜程度和声源方位对基于倾斜阵的联合估计方法定位效果的影响。仿真表明，方位与距离的联合估计算法利用小角度倾斜的垂直阵实现了二维平面声源位置的估计，且具有较高的定位精度。