基于局部线性嵌入的特征融合方法在岩石破裂状态分类的应用*

杨丽荣 江川 黎嘉骏 曹冲 周俊

(1 江西理工大学机电工程学院 赣州 341000)

(2 江西省矿冶机电工程研究中心 赣州 341000)

0 引言

在外界各种因素作用下，岩石内部会产生应力集中现象，但是这种应力集中的状态是不稳定的，因此应力会向稳定的低能状态进行过度，在过程中应变能会采用弹性波的形式向外扩散，即声发射现象[1-2]。声发射技术[3]可以预测被测对象的内部变化，是当前最佳的矿井安全检测技术[4]，且可以适用于岩石失稳的预测，提前发现危险状况。在实际监测过程中，能够准确获知挖矿过程中岩石的破裂状态，就能更快更多减少矿井安全事故发生[5-6]。岩石破裂状态的获取，需要对岩石破裂过程中的历史数据进行准确的特征向量提取。为了保留特征信号中的有用信息并对大量的数据特征进行简约，需要对特征数据进行降维处理。因此融合特征下数据降维算法的好坏对于岩石破裂状态分类及失稳预测具有重要意义。

针对原始数据特征存在大量的冗余信息、数据的数维偏高及区分性不强等问题，国内外学者对此提出了不同的解决方法。Ibrhim等[7]抽取声发射信号与力信号的各种统计参数，然后利用主元分析法(Principal component analysis,PCA)剔除冗余或与刀具磨损相关性小的信息，发现声发射信号的均值、标准偏差和力信号在三个方向分量的最大值与刀具磨损相关性最大，达到降维的目的。刘开南等[8]提出了一种用于图像分类的Mod-局部线性嵌入(Locally linear embedding,LLE)算法，通过对图像数据集进行测试，结果表明图像分类的精度较高且降维性能良好。Cheng等[9]提出了一种增量LLE算法，通过对卫星的遥测数据进行特征降维来实现故障检测，其仿真的结果表明该方案的有效性。刘杏芳等[10]通过对3D 地震数据的层问属性进行特征提取，比较LLE 和PCA 两种降维方法的聚类效果，实例应用表明LLE 算法较好地保持了原始数据的结构特征，具有更高的特征提取能力。王玥[11]使用LLE、PCA、多维缩放(Multiple dimensional scaling,MDS)几种降维算法对股票的收盘价数据进行特征简约再预测分析，并和几种直接回归预测方法进行对比，结果表明经过LLE 算法降维后的预测精度提高显著，更加精确。

通过以上分析，比较各种特征数据降维方法的优劣，发现LLE 和PCA 算法作为主流的数据处理方法已经广泛应用于科研的方方面面。通过对高维的数据进行特征简约，保留了原始数据的重要特征，使得简单模型在小数据集上有更强的鲁棒性。本文通过PCA与LLE算法的降维融合特征实验对比，分析4 个状态下融合特征的聚类效果，选取聚类效果更集中的算法作为岩石破裂信号特征数据的降维方法，为分析岩体失稳状态提供一定的理论依据和基础。

1 LLE算法原理及特点分析

针对PCA忽略原始信号的局部信息的问题，一种无监督的非线性局部嵌入算法被提出，LLE 算法的主要思想是对局部邻域线性化处理，通过将原始数据从高维映射到低维特征空间，从而使数据可视化[12]。该算法通过不同邻域的不同数据点的线性重构权值，得到局部邻域中的每个数据点，再将其映射到低维空间，同时要保证局部邻域与重构权值的关系，这样得到的低维嵌入空间的样本点线性重构权值和高维空间中表示的线性权值相同[13]。计算过程为以下3个步骤：

(1) 近邻域选择

若想要得到高维数据集X=[x1,x2,···,xn]∈RD×N各数据点的最近邻点，可以利用各数据点之间的欧氏距离来寻找，其中，点xi的k个最近邻点集合为R(xi)={xi1,xi2,···,xik}。

(2) 计算数据点局部最优近邻线性重构权值

对数据集X=[x1,x2,···,xn]∈RD×N中的所有点，给予约束条件：若是xi的近邻点，即xj ∈R(xi)，则线性重构权值表示为wij；若xj不是xi的近邻点，即xj/∈R(xi)，则wij=0。因此，可用最小二乘重构误差极小化原则来处理最佳线性重构权值矩阵：

数据点xj对xi在重构过程中的贡献为权值wij。各数据点与其近邻点之间的局部几何关系为重构权值矩阵W={wij}。由于数据点的近邻线性重构权值不会发生改变，因此当数据集发生各种变化时，重构权值矩阵都不会改变，因此，式(1)可以表达成如下形式：

(3) 求解原始信号在低维空间下的坐标

低维嵌入空间下的坐标及其近邻点的计算，必须保持高维数据空间点之间的重构权值固定不变，利用极小化误差函数求低维嵌入坐标。即：

式(3)中，yi为低维嵌入坐标；Y={yi}为低维嵌入坐标矩阵。低维坐标矩阵在进行旋转、平移要想保持不变，必须满足条件：

则计算低维嵌入坐标的极小化误差函数，式(3)可以用如下形式表示：

同理，将式(6)进行推导，把低维嵌入坐标Y求解转化为最小特征值的求解问题，即

式(6)～(7)中，M=(I -W)T(I -W)为n×n的矩阵；矩阵元素I表示单位矩阵；λ表示矩阵的特征值。M的最小d+1个特征值对应的特征向量[γ2,γ3,···,γd+1]为低维嵌入坐标Y，可表示为

根据分析LLE 算法计算步骤可知，由于低维嵌入坐标的准确性会随着k值发生变化，因此该算法的前提是需要设定每个样本点的近邻参数k，同时，近邻点数过多会导致原始数据中的非近邻点也被纳入近邻区域；近邻点个数过少会使高维原始数据集中的内在结构发生扭曲且近邻域不连通。

2 砂岩单轴压缩试验设计

2.1 岩样选择与制备

试验中的红砂岩采自两地矿山以确保实验结果的泛化能力。红砂岩G采用赣州某地质脆性粗粒红砂岩，红砂岩R 取自广西某锡矿。为达到本次试验的预期目标，将取回的岩体由钻孔取样机得到柱状岩芯，经岩体自动切割机进行分割，最后得到标准岩样50 mm×100 mm为两个端面被打磨后的岩样，具体如表1和图1所示。

图1 不同红砂岩试验岩样Fig.1 Different red sandstone test samples

表1 试验岩样规格Tabel 1 Test rock sample specifications

2.2 试验装置与参数设置

试验采用RMT-150C 型加载系统，该加载系统在刚度、静态特性和动态特性方面具有优势。伺服控制系统由液压动力源提供稳定输出，可通过行程、位移、荷载以及不同组合形式、不同加载速率的控制方式，实现单轴、三轴、间接拉伸及剪切试验等多种试验。控制模式采用位移加载，加载速率0.002 mm/s，力终点200 kN，力极限250 kN，位移终点2 mm，位移极限2.5 mm。本次实验加载如图2所示。

图2 RMT-150C 型岩石力学试验系统Fig.2 RMT-150C rock mechanics test system

多传感器集合成的应力应变采集系统包含测量垂直液压缸活塞杆的行程传感器、两种测量垂直液压缸输出力的力传感器、测量试件轴向变形轴向位移传感器。声发射传感器放置在试件中部轴线位置，试件和传感器接触部位采用真空脂作为耦合剂，最后采用透明胶布进行固定，传感器布局如图3 所示。1000 kN力传感器置于液压缸内；轴向位移传感器放置在传感器夹持器上，与上压头表面相互接触。各传感器量程范围赫尔精度如表2所示。

图3 声发射传感器布局Fig.3 Acoustic emission sensor layout

表2 应力应变采集传感器性能参数Tabel 2 Stress and strain acquisition sensor performance parameters

2.3 红砂岩破裂全过程的应力-应变特征分析

红砂岩失稳过程中垂直力和垂直形变随时间变化的数据保存在RMT-150C 型岩石力学试验系统中，通过式(9)可计算红砂岩破裂失稳过程的应力值和应变值随时间变化的关系：

式(9)中，σ为应力，MPa；F为垂直力，kN；S为横截面积，mm2。

根据式(9)绘制单轴压缩试验下红砂岩R10 和G15的应力-应变曲线如图4所示。

图4 单轴压缩下不同红砂岩应力-应变曲线Fig.4 Stress-strain curves of different red sandstones under uniaxial compression

由图4(a)可以看出，R10 岩样在应力前期，应变变化率减小，岩石内部相对变形率在应力达到12.1 MPa时逐渐保持不变，试件被破坏产生大量新的微裂纹汇合贯通的应力为45.7 MPa，轴向应变率增大。

从图4(b)可知，在预加载时，G15 岩样在未发生应变时就有一定的轴应力，此后先向上凹，斜率由小变大，在应变为0.0014、斜率为直线时应力为5.9 MPa，试件所能承受的极限为28.2 MPa，破坏后蠕变过程产生可能是加载应力和加载的持续时间导致的。

综上由R10 和G15 的应力-应变曲线可知，单轴破坏过程表现为4 个阶段。压密接阶段(OA)：岩体内部存在微小裂纹、空隙，等初始损伤受压闭合，曲线呈现上凹形状，斜率逐渐增大。弹性变形阶段(AB)：岩体由不连续状态进入连续状态，曲线呈现线性增长趋势，斜率保持不变。塑性变形阶段(BC)：曲线斜率逐渐减小到零。失稳破坏阶段(CD)：岩体强度大大降低，宏观破裂基本形成，但破裂面存在一定摩擦，且具备一定承载能力。

2.4 砂岩声发射信号时域特征提取

对于时间序列模型，目前存在的主要问题是仅对平稳过程具有较好的分析效果，对非平稳过程则表现得无能为力。而岩石破裂过程中产生的声发射信号表现为较强的非平稳过程，直接进行AR 建模效果不太理想，而经过改进的集合经验模态分解(Ensemble empirical mode decomposition,EEMD)正好解决了这一问题。因此本文在建立AR模型之前先采用改进EEMD 对岩石声发射信号进行预处理，将其分解为若干个有效的平稳的本征模态函数(Intrinsic mode function,IMF)分量，然后对各IMF 分量采用AIC 准则函数确定模型的最佳阶次，建立各个IMF 分量的AR模型，提取AR模型的自回归参数构成特征向量。

采用改进的EEMD 算法对第一破裂阶段下连续声发射时域波形进行分解，取前8 个IMF 波形如图5 所示。可以看出，IMF5～IMF8分量是原始信号中分解出的时间尺度最长、频率较低的分量，代表信号中的低频成分。

图5 改进的EEMD 算法分解后8 个IMF 波形Fig.5 Eight IMF waveforms decomposed by the improved EEMD algorithm

为了更加清晰地了解阈值选取的普遍性，采用改进的EEMD 算法分别对10 组不同岩石破裂状态下声发射信号进行分解，并求取分解出的各分量与原始信号的云相似值，最后取每组的前6 个分量的云相似值进行曲线拟合，如图6所示。

图6 各样本前6 个分量的云相似值拟合曲线图Fig.6 The fitting curve of cloud similarity value of the first 6 components of each sample

从图6 可知，前3 个分量(IMF1～MF3)的云相似值都很大。由云模型理论可知，云相似值越大则其含有原始信号的信息量越多，与原始信号的关联性更强，可以完全反映原始信号的特征。而IMF4～IMF6 的值相对较小，说明是与原始信号无关的噪声。根据多组信号统计分析，将IMF1、IMF2、IMF3确定为有效分量。

为了消除其它因素对模型的影响，建模前采用式(10)对各IMF分量进行能量归一化处理：

式(10)中，ci(t)(i=1,2,3)为改进的EEMD处理后得到的前3 个IMF 分量；ˆci(t) 为能量归一化后的IMF分量。

对砂岩同一破裂及不同破裂阶段信号经改进的EEMD分解的各IMF 分量进行AR建模，得到各分量的准则函数AIC值随模型阶次的变化。对各阶IMF分量，模型阶次n ＞5 时，AIC值变化很小而且小于n为1～5的AIC值，因此AR模型的最佳阶次为5，可建立5 阶AR 模型，提取各IMF 分量模型系数，构造15维特征向量，如式(11)：

式(11)中，φmn表示信号经改进的EEMD分解后第m个IMF分量的第n阶模型系数。

2.5 砂岩声发射信号频域特征提取

岩石破碎过程中，一些不确定因素以及岩石材料密度不均匀，导致得到的声发射信号具有较强的非线性特征。在实际工程应用中，不仅需要信号的幅度信息，还需要信号的相位信息，双谱不仅能够检测到信号的幅值，还可以得到信号的相位信息。均值为零的高斯过程，其三阶累积量、双谱均为零，因此双谱分析法能很好地消除高斯噪声。基于此，将砂岩不同破裂阶段下的信号进行双谱分析，为了消除其他条件变化对采样信号的影响，在应用双谱分析之前先对采样数据进行去均值及归一化处理，如式(12)所示：

分别对岩石不同破裂阶段下声发射信号进行双谱分析，结果如图7 所示。由图7 可知，随着轴应力的增加，声发射信号逐渐向低频扩散聚集，相比于第一破裂阶段，第二阶段在低频逐渐聚集成块，频带范围也较宽。在第三破坏阶段下，频带范围最宽，低频高频都有，且高频信息聚集；在岩样破坏后第四阶段，应力值逐渐减小，但仍具有声发射现象，但强度较弱，高频信号消失，频率主要又转向低频聚集。

图7 岩石不同破裂阶段下声发射信号的双谱图Fig.7 Bispectral images of acoustic emission signals at different fracture stages of rocks

也可直观地看出，信号经去均值及归一化处理后，砂岩声发射信号的双谱特征可以较好地区分岩石不同破裂阶段，但最终是得到双谱高阶矩阵，数据量的维数较大，不适于机器识别，因此应用奇异值分解理论对高阶矩阵进行处理，提取出多个奇异值作为最具代表性的特征向量，以便进行智能识别。

在矩阵的奇异值中，根据奇异值的大小可判断信号的种类，较大奇异值反映的是信号中的主要特征，剩余较小的部分为噪声信号。由此定义奇异谱：

式(13)中，pi表示各个状态变量在整个系统中所占能量的相对关系，也称为由矩阵A经奇异值分解得到的奇异谱。通常筛选前s个奇异谱累计贡献率大于85%的分量作为特征向量并降维，即：

经过大量数据处理发现，砂岩出于不同破裂状态时，其累积贡献率大于85%的奇异谱数量是不同的，但都分布在4～10 之间。因此，为了使构造的特征向量维数一致，统一选取前10个奇异谱构成特征向量Tho∈R1×10，

式(15)中，pi为由矩阵A经奇异值分解得到的奇异谱。

为了说明提取砂岩破裂声发射信号奇异值特征的聚类效果，将奇异谱p1、p2和p1、p3的二维分布绘成散度图，如图8 和图9 所示；结合两图分析可以看出，采用双谱奇异值分解提取的砂岩破裂各阶段特征的聚类效果明显，可以较好地区分开4 个阶段，为后续分类与识别提供依据。

图8 奇异谱p1和p2 的散度图Fig.8 Divergence plots for singular spectra p1 and p2

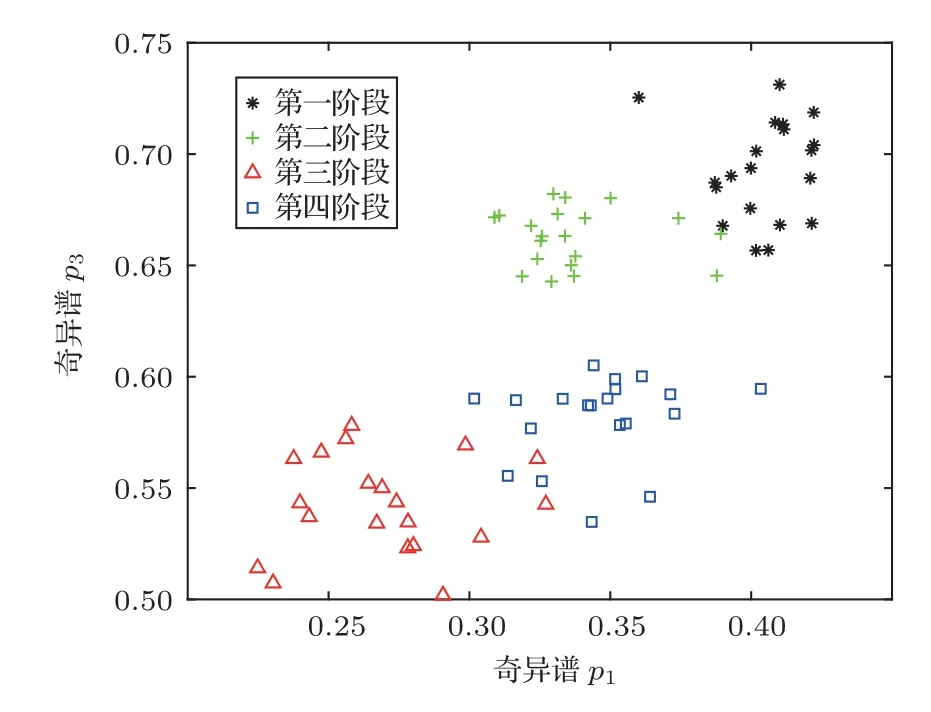
图9 奇异谱p1和p3 散度图Fig.9 Divergence plots for singular spectra p1 and p3

3 融合特征向量提取

3.1 构造联合多特征向量

(1) 采集红砂岩破裂全过程的实时数据，根据砂岩不同破裂阶段的特点来划分所采集到的声发射信号，同时读取该声发射信号所对应的应力值，构建岩石破裂状态和声发射信号之间相互对应的关系。

(2) 将实验选取的各阶段下的75组信号进行特征提取。①采用EEMD 和云相似度结合的岩石声发射信号预处理方法，由时域特征提取各IMF 分量的AR模型系数，构造15维特征向量Tar。②将砂岩不同破裂阶段下的信号进行双谱分析，并对双谱高阶矩阵进行奇异值分解，将提取的多个奇异谱值作为砂岩声发射信号频域特征向量，构造10维奇异谱特征向量Tho。

(3)将步骤(2)中 ①、②小步构造的特征向量进行首尾相连，构造如式(16)所示的联合多特征向量：

联合多特征向量T为同一个样本信号，采用不同的信号分析方法提取多个域的特征，组合为一个25维特征向量。

(4) 选取相同或不同阶段下的样本数据，重复进行步骤(2)、步骤(3)的处理，提取出对应应力此时声发射信号的联合多特征向量。

3.2 融合特征提取对比实验验证

3.2.1 PCA算法的降维特征融合实验

根据红砂岩破裂状态分类(表3)，在每个破裂阶段下，间隔均匀地选取75 组不同的数据，例如第一阶段，其应力值范围为：0～12.1 MPa，提取的样本数据对应的应力值应该尽量均匀地分布在0～12.1 MPa 下，那么将总共选取的300 组样本采用上述方法提取联合多特征向量，构成一个300×25的特征矩阵M，每个样本的联合多特征表示为矩阵的每一行。

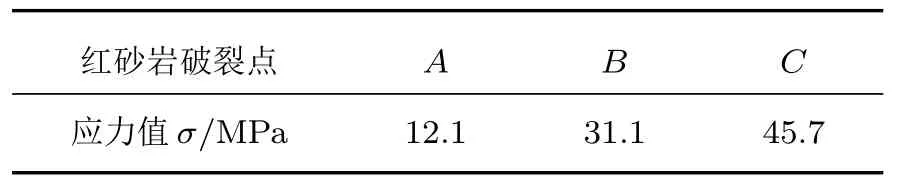
表3 R10 红砂岩破裂临界点应力值Tabel 3 R10 red sandstone fracture critical point stress value

采用PCA 对矩阵M进行特征降维，得到主元系数矩阵Coeff，即

在Coeff 矩阵中，第i列表示第i个主元成分的系数向量。此外，PCA 同时还获得了样本协方差矩阵latent，它是由15 个按降序排列的特征值构成的列向量，它们代表了每个主元对整体的贡献。所选取的主元个数按照累积贡献率大于85%的准则来确定。图10 为各主元的贡献率及累积贡献率的变化趋势。

图10 各主元贡献率及累积贡献率Fig.10 Contribution rate and cumulative contribution rate of each main element

图10 中红色柱状图代表贡献率，蓝色的曲线代表累积贡献率。从图10 中可以看出：前3 个特征值相对较大，最大为0.126；后4 个特征值趋于平稳，特征值为0.037；并且前7 个主元的累积贡献率达到88%，超过85%。因此，选取前7个主元，这样主元成分系数就变为式(18)：

对于一个新的样本，同样按照联合特征向量的方法，构造出15 维联合特征向量，然后向新的主元投影，得到降维后的特征向量Tnew∈R1×7。图11分别为提取的融合特征向量Tnew中不同主元的二维和三维分布图。

分析图11(a)和图11(b)可清晰地看出，PCA1和PCA2 主元区分的4 种状态分布较开，4 个状态有较多的混叠，且在第一状态和第四状态下会出现一个样本判别不了，而PCA1 和PCA3 主元区分的4 种状态，在第一和第二状态分布较为紧凑，第一、第三及第四状态都出现了部分样本判别不了。结合图11(c)进一步分析可知，通过使用PCA 降维后，4 种状态的三维特征分布较开，各状态有交叉混叠，然而在第一状态下，数据样本错判及漏判严重。

3.2.2 LLE算法的降维特征融合实验

采用LLE 算法对矩阵M进行特征降维，由于LLE 算法受低维子空间维数d和近邻参数k选取的影响，本文采用极大似然估计法确定砂岩破裂各状态特征数据集的低维子空间维数d。通过构建近邻间距离的似然函数，可得到全局数据结构的低维特征。

设xi为Rm独立同步的观察样本，yi为Rd中呈光滑密度f嵌入流形，则存在xi=g(yi)。假定Sx(t)是以x为球心、t为半径的小球体，构造二项式非其次过程，即

式(19)中，I{xi ∈Sx(r)}为示性函数，用泊松分布近似该过程可得

式(20)中，V(d)为d维空间下球的体积函数。令θ=lg(f(x))，则N(t)的似然函数可表示为

式(23)中，Tk(xi)是样本点xi与第k个近邻点的欧式距离。分别求解每个样本点对应的特征维数，并计算其平均值，将其当作全局特征维数d，即

通过上述极大似然估计法计算砂岩声发射信号特征数据集的低维子空间维数d=4，因此，利用LLE算法对样本数据降维后得到4维的融合特征向量。

由于不同近邻参数取值会对所得融合特征产生影响，为分析其不同取值的影响效果，先选择固定本征维数d=4，然后改变近邻参数k的取值，利用支持向量机(Support vector machines,SVM)对融合特征向量进行特征识别，评价标准为各个阶段的识别准确率。图12为不同近邻参数k下各阶段识别率曲线关系。

图12 不同近邻参数下各融合特征的敏感度之和Fig.12 The sum of the sensitivities of each fusion feature under different neighbor parameters

由图12 中可以看出：随着k值的变化，降维后所得到的融合特征经SVM 识别后，识别率发生较大波动，第二阶段下识别率明显偏高，且当k=5时，4 个阶段的识别率都达到最大，分别为0.84、0.88、0.84、0.8。因此确定近邻参数k=5，此时LLE 算法降维后融合特征的聚类效果如图13所示。

图13 LLE 算法降维后的融合特征的聚类效果Fig.13 Clustering effect of fusion features after dimension reduction of LLE algorithm

从图13(a)和图13(b)可以看出：dim1 和dim2特征区分得第一阶段与后三个阶段分布相隔较远，而dim1 和dim3 特征区分的4 种状态分布都靠的比较近，呈一条水平线趋势，且各状态交叉混叠数目较少，只有在第四状态下存在一个样本判别不了。结合图13(c)可以看出，第一状态没有一个样本错判，且4 个状态相比于PCA降维后的聚类效果更集中。

4 两种算法融合特征值的敏感度对比分析

为了更好地比较两种降维方法的优劣，利用散步矩阵法计算PCA 及LLE 算法在d=4、k=5参数下对矩阵M降维后的融合特征的敏感度之和。散布矩阵包含类间和类内两种散布矩阵，特征的散布值可由这两个矩阵分析得到。设有M类破裂状态，每种状态的样本数为N。原始特征向量x=(x1,x2,···,xD)，原始特征向量的维数用D表示。

类间散布矩阵：定义一个Sb，表达式如式(25)所示。特征的类间散布值越大，其类间辨识度则越好。

式(25)中，ui表示第i类特征值的均值；uo表示总体样本的全局均值向量。

类内散布矩阵：同理定义一个Sw，表达式如式(26)所示。特征的类内散布值的大小，代表特征的类内聚集度好坏，越小代表聚集度越好。

根据这两种矩阵的分布特性，定义评价特征优劣的敏感度算法，如式(27)所示：

式(27)中，tr(Sb)和tr(Sw)分别表示Sb和Sw的迹。当Sb越大或Sw越小时，φ也越大，表明该特征对砂岩破裂状态分类性能越强，反之则越弱。通过式(27)计算两种算法下各融合特征的敏感度，结果如表4 所示。

表4 两种算法降维后融合特征的敏感度之和Tabel 4 The sum of the sensitivities of the fusion features after dimensionality reduction of the two algorithms

由表4 可以看出：经过LLE 算法降维得到的融合特征值的敏感度比PCA算法近乎两倍大。前3个特征值的敏感度逐渐减小，第四个特征的敏感度增加，与PCA算法得到的融合特征值的敏感度的变化趋势几乎一样，呈现先减小后增大，且融合特征敏感度之和远远大于PCA 算法，说明经过LLE 算法降维后得到的融合特征更多地表征了原始信号包含的局部信息。图11(c)和13(c)也证明了LLE算法相比PCA算法具有更好的聚类效果，为后续砂岩破裂状态识别分类的准确性提供了有利的验证。

5 LLE特征融合下的砂岩破裂状态分类实验验证

分别将得到的时域、频域及融合特征向量分为两组，用于训练和验证。训练样本数为300 个，每类样本为75 个；测试样本数为100 个，每类样本为25个。使用训练样本的特征集训练基于PSO-LSSVM分类器，并优化LSSVM 中参数σ和γ，设定PSO 算法中的局部搜索能力c1为1.5，全局搜索能力为c2为1.7，种群数量为50，迭代次数为200，迭代曲线如图14所示。

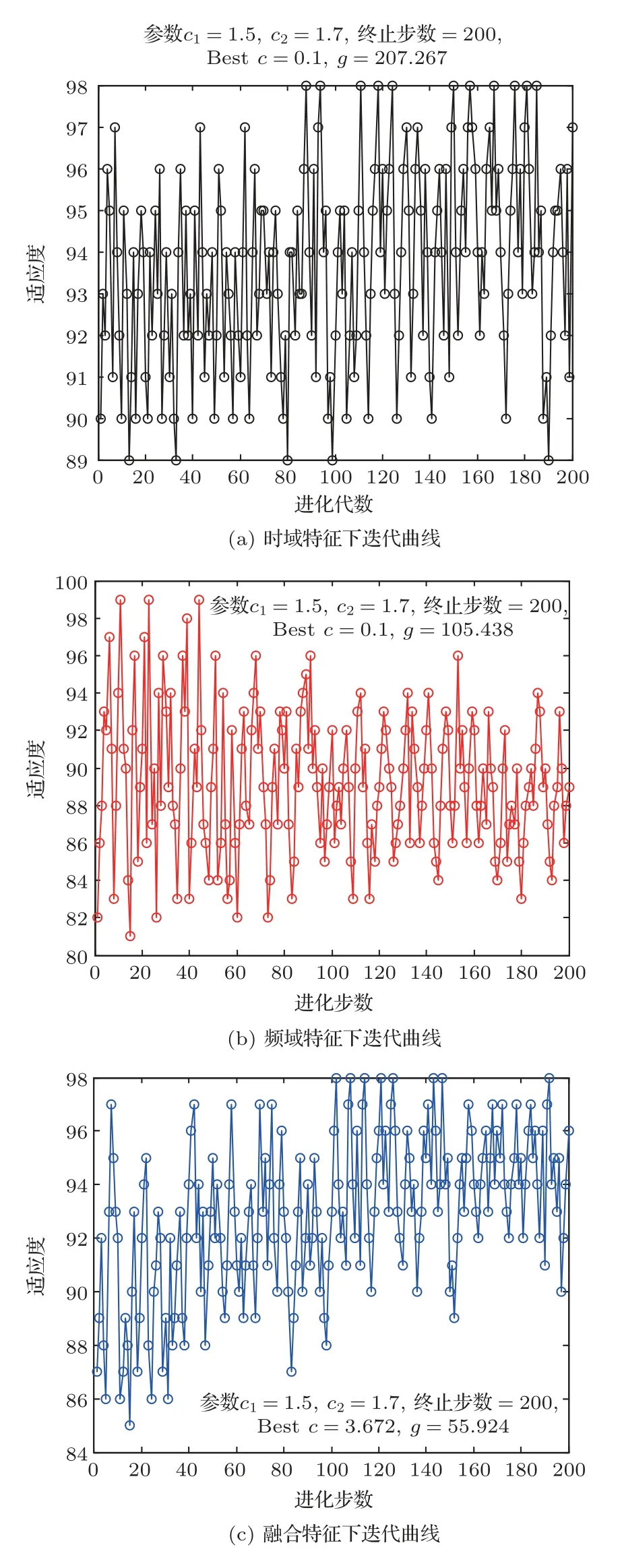
图14 各域特征迭代曲线图Fig.14 Iterative graph of each domain feature

由图14 可知，在时域特征集下搜索到的最佳惩罚因子γ=0.1，σ=207.267；在频域特征集下搜索到的最佳惩罚因子γ=0.1，σ=105.438；在融合特征集下搜索到的最佳惩罚因子γ=3.672，σ=55.924。进一步对比分析得到融合特征下迭代适应度更集中，分布在90～98之间。

将测试样本特征集放入训练好的PSO-LSSVM多模式分类器中进行分类预测。由分类器的输出值来确定岩石破裂状态类型。设定1 表示压密阶段，2表示弹性阶段，3 表示失稳破坏阶段，4 表示失稳破坏后阶段。图15 为时域、频域及融合特征向量集经PSO-LSSVM算法分类的结果图。

图15 各域特优化后的结果分类图Fig.15 Result classification diagram after optimization of each domain

图15 中蓝色*型和红色°型分别表示测试样本预测与实际类别。由图15 可知：各域特征集经PSO-LSSVM 优化分类，只出现少数样本错分，而LLE 降维后得到的融合特征集经PSO-LSSVM 优化后识别效果最理想，计算各阶段的分类识别率如表5所示。

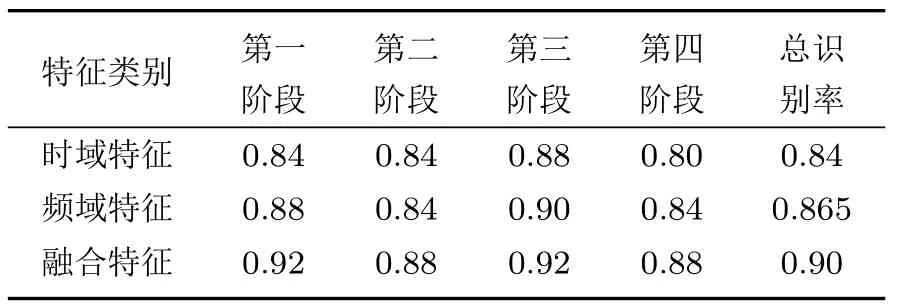
表5 不同特征的识别率比较Tabel 5 Comparison of recognition rates of different features

对比时域特征、频域特征及融合两域特征的识别率，采用融合特征下的总识别率为90%，较单一的时域特征识别提高了6%，可知，使用LLE 算法对信号的联合特征进行数据降维用于岩石破裂状态分类可以有效提高系统识别率。同时该方法可以将特征中次要成分去掉，降低了特征向量的维数，大大减少了后续训练及识别的时间，避免了“维数灾难”的发生。

6 结论

(1) 通过单轴压缩试验，计算红砂岩破裂失稳过程的应力值和应变值随时间变化的关系，得到不同砂岩失稳过程的应力应变曲线，通过比较分析，将砂岩破裂失稳划分为4 个阶段，并分析各阶段下岩石内部状态变化，为预测砂岩破坏失稳提供依据。

(2) 将构造的时、频域联合多维特征向量采用PCA 方法和流形学习LLE 算法进行特征约简，比较发现LLE 算法降维后融合特征向量的聚类效果更好，样本错判漏判现象较少，且LLE 算法降维后的融合特征的敏感度之和远大于PCA方法，表明该融合特征更多地包含了原始信号的局部特征信息。

(3) 利用粒子群优化最小二乘支持向量机算法进行岩石破裂状态分类，比较分析基于粒子群改进的最小二乘支持向量机算法对单一特征与经LLE算法降维融合特征下的分类识别率，可以得出采用融合特征后的分类识别率显著提高且识别的效果明显要优于单一特征识别。表明，充分考虑多个域特征向量之间相互制约和影响的关系相较于单一特征向量，在岩石破裂状态分类方面具有更为准确的预测结果。