嵌入物理约束的3D CNN在流场预测中的应用

张 洋,秦文瑾,李 庆,董 雪*

(1. 上海交通大学中英国际低碳学院,上海 201306;2. 上海理工大学机械工程学院,上海 200093)

1 引言

在航空[1]、医疗、工业燃烧等研究领域中,流动[2]起着重要的作用。Duraisamy等[3]指出湍流建模数值模拟发展的过程中,机器学习提供了有效的策略来构建大型数据集和目标变量之间的映射,机器学习可以作为“黑盒子”来与现有的模型进行结合以提供后验校正。

现有的深度学习模型往往采用模拟数据对神经网络进行有监督训练,然而实际工程应用中往往难以获得流场和压力场等信息作为模型监督[4]。Navier-Stokes方程组(简称N-S方程组)描述了流体的浓度、流速、压力、特征长度、动力粘度等物理量之间的关系,对于欠约束的物理场景,可以借力于N-S方程组,对神经网络进行约束。

但目前基于物理约束的研究多数局限在多层感知器(Muti-Layer Perception,MLP)或者使用二维卷积神经网络(Convolution Neural Network, CNN)研究稳态问题。Raissi等人[5]提出了Hidden fluid mechanics(HFM)的概念,借助N-S方程组,通过MLP的反馈特性,实现了压力场和速度场的预测。但在约束方程中雷诺数和佩克莱数在网络中被限制为一个常数,而实际上这两个无量纲数为时空变量,因此在对应参数变化大的场景中将表现出较差的适用性。另外MLP的计算效率较低,譬如随着流场区域的变大,MLP的训练参数将会急剧增大,且MLP会丢失图像(二维物理场)的空间特征。对于使用传统的2D CNN的方法,由于湍流流动中在时间维度上也需要获得连续性信息,如果仅能在图像的长和宽两个维度获取梯度信息,不足以将含有时序信息的微分方程约束嵌入神经网络中。

而有时序的流场信息可以看作是三通道输入数据,对三通道输入数据使用三维卷积核在三个方向进行卷积可以有效获取特征图对时间的导数。综上,此本研究将开发一种基于三维卷积神经网络的弱监督学习模型,并对DNS算例中的流场散点数据进行均匀网格化、无量纲化处理,以将其转换为可进行卷积操作的数据集。该模型将以N-S方程组为物理约束,对神经网络进行构建,以实现对流场从浓度场到速度、压力场的映射。

2 研究方法和实验准备

2.1 物理约束方程

计算流体力学常用的控制方程有传质方程、动量守恒方程、连续性方程,对这些控制方程进行无量纲化可以简化问题,并减少所需考虑的参数的数量,并使得神经网络在学习过程中聚焦于特征长度、特征速度等无量纲量,从而减少神经网络对具体案例数据的依赖,有利于增强神经网络的泛化能力。

借由雷诺运输方程,传质方程可以写成如下的无量纲形式

ct+ucx+vcy+wcz=Pe-1(cxx+cyy+czz)

(1)

同样借由无量纲化的动量守恒方程和连续性方程,可以得到:

ut+uux+vuy+wuz=-px+Re-1(uxx+uyy+uzz)

vt+uvx+vvy+wvz=-py+Re-1(vxx+vyy+vzz)

wt+uwx+vwy+wwz=-pz+Re-1(wxx+wyy+wzz)

ux+vy+wz=0

(2)

Re和Pe分别代表雷诺数和佩克莱数,分别由UL/v和UL/k定义,其中U和L分别是特征速度和特征长度,v和k分别是动力粘度和质量扩散系数。可以通过神经网络和建立残差标准完成如下映射

(t,x,y,z)→(c,u,v,w,p)

(3)

其中残差标准的一个参考形式如下

e1=ct+ucx+vcy+wcz-Pe-1(cxx+cyy+czz)

e2=ut+uux+vuy+wuz+px-Re-1(uxx+uyy+uzz)

e3=vt+uvx+vvy+wvz+py-Re-1(vxx+vyy+vzz)

e4=wt+uwx+vwy+wwz+pz-Re-1(wxx+wyy+wzz)

e5=ux+vy+wz

(4)

上述残差中所需要的偏导数可以通过神经网络中自微分的链式法则或差分形式的固定卷积核进行求取。故对于映射目标的c,u,v,w,p,可以以最小化上述残差e1,e2,e3,e4,e5的均方差为目标进行网络训练。

2.2 实验数据准备

本研究的实验数据,二维圆柱绕流算例的设计思路来自Raissi[5]的HFM文献,本研究采用OpenFOAM对流场数据进行复现。流场在x方向取切片[-2.5,7.5],y方向取切片[-2.5,2.5],空间分辨率为0.05m,时间分辨率为0.08s。圆柱圆心与坐标系原点重合,半径为0.5m。雷诺数取100。并假设无量纲自由流速度为U=1,运动粘度ν=0.01,系统表现出周期性稳态行为,其特征在于尾流中的不对称涡旋脱落模式。为了使用数值求解器生成数据,本研究在圆柱壁上使用零滑移和零浓度边界条件。对于佩克莱数,本研究设定为100,因为对于以烟雾为主体的空气流动[6]而言,雷诺数和佩克莱数是大体相等的。

2.3 实验数据预处理

对于实验数据的预处理主要包括如下两个部分:

1)无量纲化

基于数据无量纲化的要求,对OpenFOAM生成的数据需进行无量纲化处理,特征速度取入口处速度,特征长度取单位1,特征密度取实验温度下流体平均密度。参考如下公式进行无量纲化

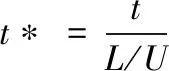
(5)

2)均匀网格化和补零

对于传统的计算流体力学研究而言,生成的流场数据通常是散点数据。研究中常常需要根据感兴趣区域对数据的空间分辨率做调整,这意味着它不能直接被应用于卷积神经网络里,因为卷积神经网络的输入数据一般要求是均匀网格化的图片数据。所以对于已经获取的流场散点数据,需要对其进行均匀网格化处理。原始数据由直角坐标系下的低分辨率数据和圆柱边界附近极坐标系的高分辨率数据组成,为了使数据能直接输入到卷积神经网络中进行训练,对极坐标系下的加密数据进行去除。同时因为原始数据中并没有圆柱内部的流场分布,为了形成的完整的网格化数据,需要对圆柱内部进行补零操作。

3 基于三维卷积的流场预测神经网络

3.1 神经网络设计与数据集准备

式(4)中多次用到了特征图对时间和长宽三个维度的偏导数,由于2D CNN无法直接获得时间维度上的导数,故本研究选用三维卷积神经网络进行训练。本研究所设计的3D CNN神经网络结构如图1所示,分为编码和解码过程。编码过程使用多帧连续的浓度场信息作为输入,并采用50%重叠的采样进行DataLoader定义。模型输入为一个三维张量,可以表示为si,j,k=D(i,j,k),其中i=201,j=101,k=8。本研究的数据集包括201帧图像,故总数据量分割后共有50个样本。卷积过程采用三维卷积。编码特征向量hvec(s)可以表示为式(6)[7]

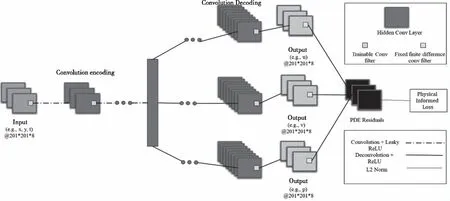
图1 3DCNN网络示意图

hvec(s)=ConvNN(s)

(6)

其中ConvNN(s)表示使用多个3D卷积层和最后的全连接层实现的从输入si,j,k到特征图的映射。每个卷积层后都会采用BatchNorm实现正则化,随后以LeakyReLU作为激活函数。

解码过程则是通过反卷积操作来构建多个堆叠的解码层。因为输出分别是U,V,P三个独立的场,所以采用三个独立的解码器来实现从特征图到预测分布的映射。解码过程可以表示为式(7)

(7)

对于CNN的求导,本网络中采用差分形式的卷积核对网络预测的U,V,P通过固定卷积进行导数求取[9]。

对于中心点,采用四阶中心差分进行导数求取,如式(8)所示。

(8)

对于边界点,采用三阶单边迎风/逆风差分公式进行求取,如式(9),所示。

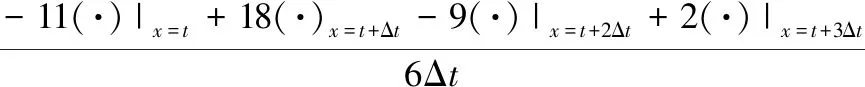
(9)

3.2 训练与预测

网络的损失函数将由多个部分组成,分别是真值监督、边界条件约束、物理边界约束、物理方程约束。各个部分均采用均方误差函数(Mean Squared Error, MSE)作为评估标准,MSE的原理如式(10)所示

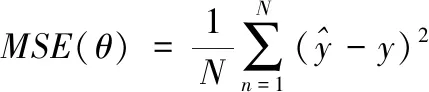
(10)

其中真值监督使用U的实验模拟数据作为监督,边界条件使用图像四条边框的真值作为监督,边框厚度为10个像素。物理边界约束使用圆柱边界厚度为10个像素的真值作为约束,物理方程约束采用式(4)的残差作为约束,故损失函数可以用式(11)进行表示

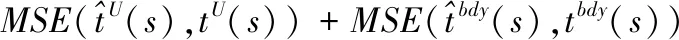
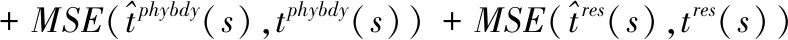
(11)

网络训练后的权重将可以从输入的多帧浓度场计算出对应帧的速度场和压力场。

词语的文化义多是词义、语素义、语境义演变的结果，反映民族的认知，“柳”文化内涵丰富，与中华民族的生理——心理认知、修辞认知、转喻、对自然的崇拜和外来文化的影响密切相关。

3.3 实验条件与评价指标

本文中深度学习网络的训练环境为CentOS 7.4,使用Pytorch框架进行训练;算力为4块NVIDIA GeForce GTX 2080Ti GPU显卡。本文中网络训练使用标准的Adam训练模型,基础学习率为1e-5,批量大小(Batch Size)设置为16,训练20000个epoch。

对模型效果的评估采用均方误差(MSE),结构相似性(SSIM),峰值信噪比(PSNR)三种方案对结果进行评估,其评估方式分别如下所示。

(12)

(13)

4 结果及分析

4.1 模型预测结果及与MLP对比

本文提出的3D CNN网络总参数量为159,242,310,参数内存为607.46MB。如图2所示,网络在10000个epoch后已经收敛。时间效率上,MLP算法训练此算例所需时间为40h,而本文算法训练此算例所需时间为24h,效率提升了40%。

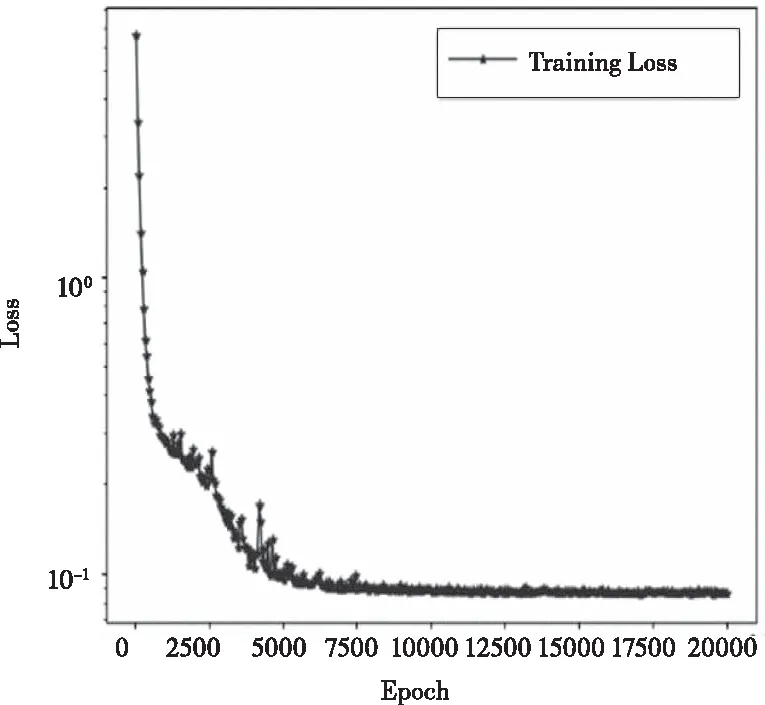
图2 网络训练的收敛曲线

三维卷积神经网络预测结果的准确率分析如表1所示。模型的MSE误差分布上,U场因为是强监督,最接近真实值,V场和P场则次之。SSIM的结果分布也符合此规律,但是SSIM的结果却明显比MSE优异,这是因为MSE对于局部较大噪声所产生的误差惩罚很为严重。PSNR的结果也说明模型的整体预测结果良好,同时PSNR在P场预测结果的优异性,说明了在P场的预测结果也具有说服力和有效性。由此可见,本文的预测结果误差较小,这是因为3D CNN能够很好的利用原始数据在时间维度上的分布信息。

表1 三维卷积神经网络预测结果的准确率分析(浓度场输入,U场强监督)

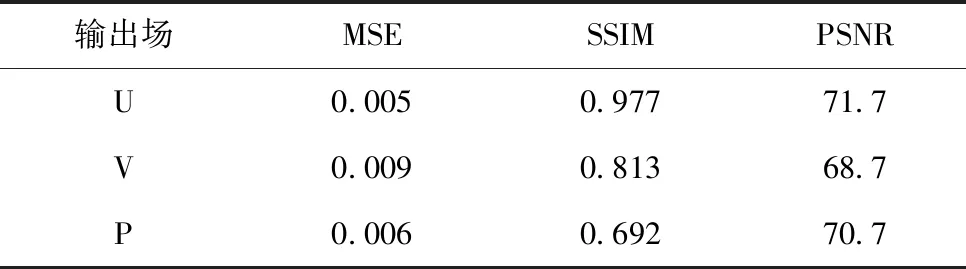
输出场MSESSIMPSNRU0.0050.97771.7V0.0090.81368.7P0.0060.69270.7

4.2 预测结果在时间分布上的分析

由于二维圆柱绕流时间上呈周期性,将预测结果的误差在时间维度的分布进行描述有利于验证时间分布的连续性和周期性。本算例的时间分辨率为0.08s,预测的结果如图3所示。

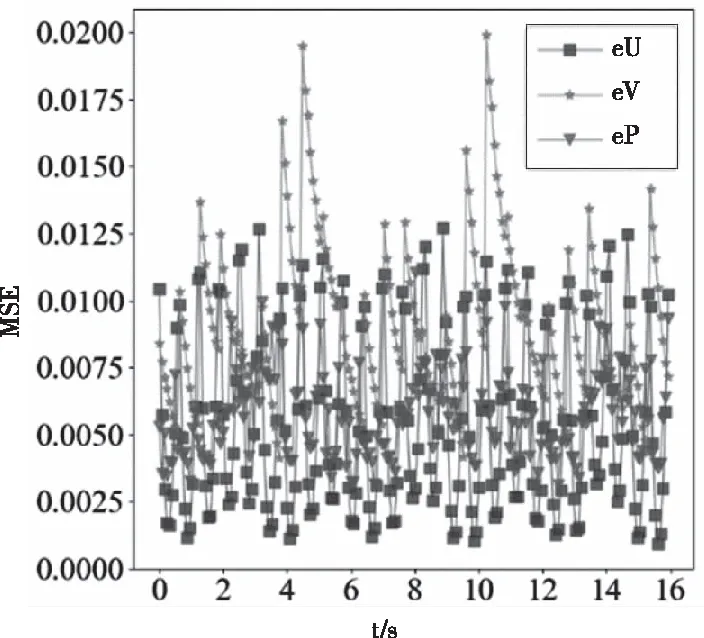
图3 预测U,V,P场的MSE随时间分布情况(输入为浓度场,强监督为U场)

结果显示,预测的结果在U,V,P场的分布均具有周期性,周期约为5s。权钲杰[10]指出以MSE为损失函数的预测方法对复杂样本中存在的噪声无法进行有效的剔除,预测结果周期性的性能下降也可能是由于原始数据周期性的噪声。

4.3 预测结果在空间分布上的分析

对于二维圆柱绕流算例,研究更关注的是圆柱附近的流动情况,对预测结果进行空间分割将有利于评测结果的准确性在空间上的分布。算例中的圆柱位于(0,0)位置,半径为0.5m。

在X轴方向上的误差分布中,如图4所示,速度场和压力场在圆柱附近和右侧都出现了较高的预测误差,这与前文中可视化的结果是一致的。其中圆柱附近的误差主要是由于出现了速度场和压力场的边界骤变,在神经网络的学习中,更复杂的场景需要更高分辨率的数据集。而右侧边界中对于圆柱绕流算例的研究并不重要,对于结果的整体影响可以忽略。且可以明显看出造成V场MSE结果较差的原因就在于V场右侧的误差突变。

图4 预测结果MSE沿X轴方向的分布情况 (输入为浓度场,强监督为U场)

因为该算例的流体主要流动方向为X方向,所以其在Y轴方向上的分布上具有一定的对称性,如图5所示。U场在圆柱边界的误差会更大,这是由于流动在此处此方向上变化最剧烈。

图5 预测结果MSE沿Y轴方向的分布情况 (输入为浓度场,强监督为U场)

5 结论

对于流动的建模一直是流体力学中的重要部分,相比计算流体力学,结合机器学习方法的数值建模方法具有更强的时间效率。本文针对现有神经网络建模模型所存在的不足,提出了嵌入物理约束的三维卷积神经网络结构。

通过本文的研究和分析可以得出如下主要结论:

1)现有的神经网络模型在湍流预测中依然存在较大的不足和局限性,主要体现在基于MLP的网络结构计算效率的不足和以基于2D CNN的网络结构无法很好的利用时序信息。

2)本文所开发的3D CNN,能够在利用时序信息的同时发挥CNN在神经网络学习中的优势。其在二维圆柱绕流算例上的结果在MSE,SSIM和PSNR三个独立指标下呈现的准确性和效率说明了该理论的可行性。3D CNN的训练时间效率相较于MLP提升了40%,是更为高效的算法。

未来,本文将研究如何提高模型的泛化能力,提高边界预测的准确性。