高速钢轨RCF裂纹涡流检测仿真系统及应用

于亚婷,袁 飞,熊龙辉,田贵云

(1. 电子科技大学机械与电气工程学院,四川 成都 6117312. 中国铁道科学研究院集团有限公司基础设施检测研究所,北京 100081;3. 电子科技大学自动化工程学院,四川 成都 611731)

1 引言

中国高铁规划建设起步较晚,但从2003年第一条高铁—“秦沈客运专线”建成到2020年底,我国铁路运营总里程预计将达到14.6万千米,最高时速可达到350千米/时[1-2]。高速铁路的快速发展满足了人民群众出行、运输需求,顺应我国经济快速发展要求。然而,高铁事故的发生直接危害到生命财产安全,所以对高速轨道服役期间的损伤进行快速定期检测和维护工作是重中之重[3]。目前常见的高铁钢轨伤损有滚动接触疲劳损伤、内部核伤、腐蚀裂纹等。其中,钢轨滚动接触疲劳(Rolling Contact Fatigue:RCF)伤损最为常见,其包括轨头表面的斜裂纹、轨头内部隐伤和轨头的剥离掉块三种类型[4]。

目前,我国高速钢轨常用的材料为U71Mn、U75V和U76CrRE三种钢种,不同钢种的化学成分占比不同,其中,U76CrRE的主要成分包括C、Si、Mn、Cr等[5],该合金钢具有很强的导电性和导磁性。针对高导电性和高导磁性材料,电磁无损检测被证明是最有效和最适合的方法[6]。但是针对高速钢轨疲劳接触裂纹的电涡流无损检测技术中涉及动态/静态问题、电场和磁场的耦合问题,还需开展进一步的研究。

目前针对在静态情形下的电磁无损检测电磁场的计算,Dodd和Deeds、Theodoulidis、李勇等[7-12]基于电磁场理论建立不同的解析模型,结合分离变量法和截断区域法等数学方法得到解析表达式。然而建立的解析模型大都是针对无裂纹的金属构件展开的。为了对高铁轨道疲劳接触裂纹的检测提供理论支持,作者和Theodoulidis等人推导了含有圆柱裂纹、椭圆柱裂纹和矩形裂纹的金属构件电磁无损检测电磁场解析计算表达式[13-14],然而电磁场的解析计算涉及电磁场、数学、数值计算等多学科基础理论,因此计算过程繁复。

同时,针对高速运行情况下钢轨裂纹的无损检测,作者等提出基于动生涡流的直流电磁无损检测方法是实现金属构件中裂纹快速检测的可行方法[15]。对高速运行下含裂纹钢轨的直流电磁无损检测的电磁场进行数值模拟是认识和理解在运动情形下钢轨中电磁场分布的重要手段。然而,基于动生涡流的直流电磁无损检测电磁场仿真建模过程因涉及瞬态分析、涉及多个物理场,所以建模过程较为复杂,计算时间较长。

为此,为深入理解电涡流无损检测中电场和磁场的耦合关系,理解静态和高速运行状态下高速钢轨中电磁场的分布,有必要构建高速钢轨疲劳接触裂纹电涡流检测评估仿真系统,降低电涡流无损检测中静态电磁场解析计算复杂程度以及动态电磁场的建模难度。提升获取静态电磁场和动态电磁场分布的效率,为提出高铁钢轨中疲劳接触裂纹的定量无损检测方法提供支撑。为此,本文基于.NET技术设计了静态和动态情形下高速钢轨滚动疲劳裂纹的电涡流无损检测评估仿真系统,旨在避免复杂推导过程和复杂建模过程的情形下,充分理解含有裂纹的金属构件在动/静态电磁无损检测中电场和磁场的耦合规律,最后将该系统应用于确定动/静态情形下电磁场的分布和RCF参数之间的定量关系。

2 基础理论

2.1 含裂纹金属构件电涡流无损检测静态电磁场计算方法

涡流检测技术是利用电磁感应原理,通过测定被检工件内感生涡流的变化来无损评定导电材料及其工件的某些性能,或发现裂纹的无损检测。在涡流检测技术中,当线圈中通入交流电后线圈周围将会产生磁场,变化的磁场感应被测的金属试件表面产生涡流,变化的涡流产生二次感应磁场与原磁场叠加使线圈的复阻抗发生变化,当金属试件有裂纹时,通过检测线圈的复阻抗的变化或者磁传感器电压的变化检测该试件的裂纹参数,其检测原理过程如图1所示。

图1 电磁涡流检测基本原理

为模拟钢轨中的真实裂纹,作者建立了含有矩形裂纹的金属构件的电磁无损检测电磁场解析计算模型[13]。主要思路如图2所示。首先计算含有圆柱裂纹的金属构件的电磁无损检测电磁场解析计算表达式。然后通过最小误差法将其扩展到含椭圆柱裂纹的电磁无损检测电磁场解析计算表达式。最后通过面积相等、裂纹长、宽与椭圆长轴和短轴成比例的等效方法获得含有矩形裂纹的金属构件电磁无损检测电磁场半解析计算模型。其中含有柱状裂纹的金属构件的电磁涡流电磁场计算是获取含矩形裂纹金属构件电磁无损检测电磁场计算关键。

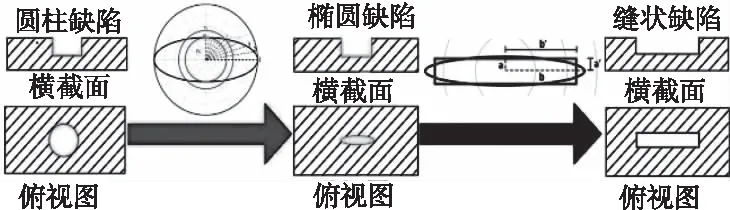
图2 含矩形裂纹的金属构件电磁无损检测电磁场计算思路

2.2 基于直流电磁激励动生涡流的钢轨RFC裂纹检测原理

动生涡流是指当电磁检测装置(探头)与金属构件之间存在相对运动时,金属构件表面所产生的涡流。根据法拉第电磁感应定律,金属构件表面的动生涡流可表示为

Jm=σv×B

(1)

动生涡流检测技术是指在激励线圈中通入直流电产生恒定磁场,通过探头与金属构件(例如钢轨)之间的相对运动在金属构件表面产生的动生涡流而对金属表面裂纹进行检测,如图3所示。在动生涡流检测系统中,根据麦克斯韦方程组以及式(1),探头与运动金属构件的控制方程可写为:

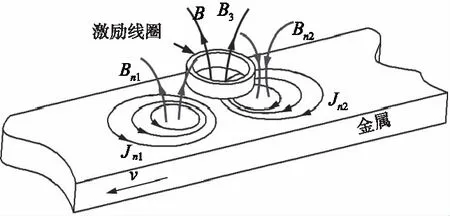
图3 动生涡流裂纹检测磁场图

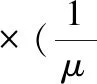
(2)

式中,μ为金属构件的磁导率,A为磁矢量势(B=∇×A),J0为激励线圈所产生的恒定磁场。

根据楞次定律,图3中动生涡流Jm可表示为Jn1和Jn2,Jn1和Jn2方向相反。Jn1和Jn2产生磁场分别为Bn1和Bn2,其方向由安培定律确定。如金属构件为钢轨等铁磁性材料,铁磁性材料将会被检测系统内部的磁场磁化而产生磁化场,记为B3。因此,根据式(2),当金属构件表面不存在裂纹时,动生涡流检测系统中的综合磁场Bc可表示为

Bc=B+Bn1+Bn2+B3

(3)

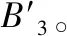
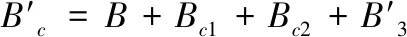
(4)

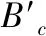
3 仿真系统结构

3.1 仿真系统需求分析

自然基金委重大仪器专项采用低速精检和高速巡检的方案实现对高速钢轨中疲劳接触裂纹的检测与评估。为此,一方面需要从理论上深入理解在静态/准静态情形下,电场与磁场相互作用的物理基础理论,实现电磁场的解析计算;另一方面需要深入了解在高速运动状态下,钢轨中含RCF裂纹时,动生涡流的分布规律及RCF裂纹对磁场的影响。为此,需要构建动静态电涡流无损检测评估仿真系统,为RCF裂纹的定量检测评估、探头设计以及试验验证提供支持。另一方面,通过理论分析和文献[18]可看出,对于静态电磁场,当金属构件存在裂纹时,其计算精度较高,且计算效率得到大大提升(约为数值计算的30倍),但其计算过程较为复杂、涉及电磁场和数学知识众多,晦涩难懂。为此有必要通过电涡流检测评估仿真系统将整个计算过程封装,降低计算难度,并在保证计算精度的情况下可快速地获取不同裂纹参数下的磁场。

高速运行下产生的动生涡流可用于钢轨表面裂纹的快速定量检测,但目前对运动状态下动生涡流的分布、电磁场的分布等缺乏直观认识。虽采用ANSYS Maxwell可实现运动情形下的电磁场仿真,但瞬态分析所需时间长,建模过程复杂,对分析人员的数值建模理论要求较高,为此有必要简便快捷地可视化展示运动速度和钢轨疲劳裂纹参数对电磁场分布的影响,帮助设计人员理解运动速度对检测的影响。

3.2 电涡流无损检测评估仿真系统体系结构设计

结合3.1节的系统需求分析,构建钢轨滚动RCF裂纹的电涡流无损检测评估仿真系统的框架,如图4所示。

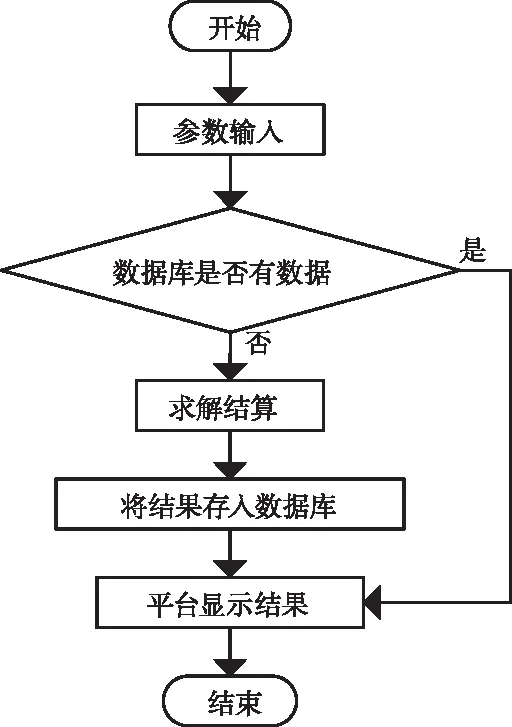
图4 电涡流无损检测系统框架

该仿真系统由高速钢轨RCF裂纹的电磁场静态计算模块、直流无损检测2D仿真模块和直流无损检测3D仿真模块组成,分别实现对含RCF裂纹的电涡流磁场的快速解析计算及高速运行情形下电磁场和动生涡流、速度效应的计算和可视化。该系统不仅可为静态和动态下钢轨滚动RCF裂纹定量检测提供支撑,也可为涡流无损检测正向/逆向问题研究、传感器探头优化设计及试验验证提供支持。

3.3 电涡流无损检测评估仿真系统详细设计

3.3.1 含RCF裂纹钢轨静态电磁场解析计算模块

基于电涡流无损检测电磁场解析计算的基础理论,为实现电磁场的解析计算,文中将曲面钢轨简化为平面金属,将钢轨中的疲劳接触裂纹简化具有矩形截面的直裂纹,利用MATLAB编写2.2节解析计算函数代码,实现对磁矢量势的解析求解。

在实际工程中,钢轨RCF裂纹参数在一定范围内变化[16];为克服C#单独链接MATLAB编写的m文件计算效率低的问题,本文采用数据库技术将解析计算的磁矢量势、磁感应强度等保存在数据库中。当进行解析计算时,根据输入参数先通过数据库查询是否有对应的解析结果,如果有则直接调用,实现解析结果的快速调用与显示;否则,调用MATLAB编译的DLL文件计算含RCF裂纹钢轨电涡流无损检测电磁场,将解析计算结果保存于数据库并显示计算结果。该计算流程如图5所示。

在C#上调用MATLAB函数时,需先配置MATLAB运行环境变量,保证C#能在path环境变量中找到DLL文件;然后编写磁矢量势数值计算求解函数;通过MATLAB的deploytool命令将解析函数生成DLL文件(环境需选择.NET Assembly环境);创建C#项目导入编译的DLL文件,根据不同项目功能编写相应函数,实现在C#平台上对特征值的求解和钢轨RCF裂纹模型的解析计算,如图6所示。

将MATLAB的计算结果存储于数据库前需先配置相关的数据源,将数据存储于指定的数据库;链接建立完成后,执行数值插入的SQL语句;可执行SQL查询语句查看数据库调用结果,具体过程如图7所示。

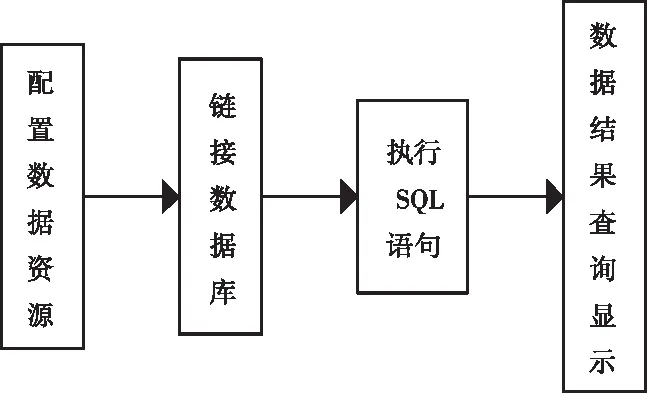
图7 MATLAB数据存储于数据库的过程

3.3.2 高速钢轨RCF裂纹直流电磁无损检测2D仿真模块

对钢轨滚动疲劳接触裂纹的动生涡流无损检测2D仿真是基于ANSYS Maxwell完成的。其中钢轨RCF裂纹类型及参数如表1所示。为实现对高速运行情况下含裂纹的钢轨疲劳裂纹的检测,分析时需设置静态区域和动态区域,其中探头和空气所在区域为静态区域,钢轨所在区域为动态区域,如图8所示。在静态区域,探头固定不动,而在动态区域内,钢轨以速度v沿X轴负向运动。在求解过程中,静态区域网格不发生变化,而在动态区域内,由于探头和裂纹的相对位置不断改变,每个时间步下动态区域内的网格都需重新划分,且各区域磁场在两个区域的边界处实现传递,以完成在该时间步下的磁场计算,因此,建模难度较大。为此,本文基于C#的WinForm平台结合ANSYS Maxwell搭建钢轨滚动疲劳接触裂纹电磁场的2D动态仿真模块。该模块将复杂建模过程进行封装,用户只需输入模型参数、网格参数、计算参数,就可实现对2D动态磁场仿真,避免仿真中繁琐的步骤和建模失误等对计算结果的影响。

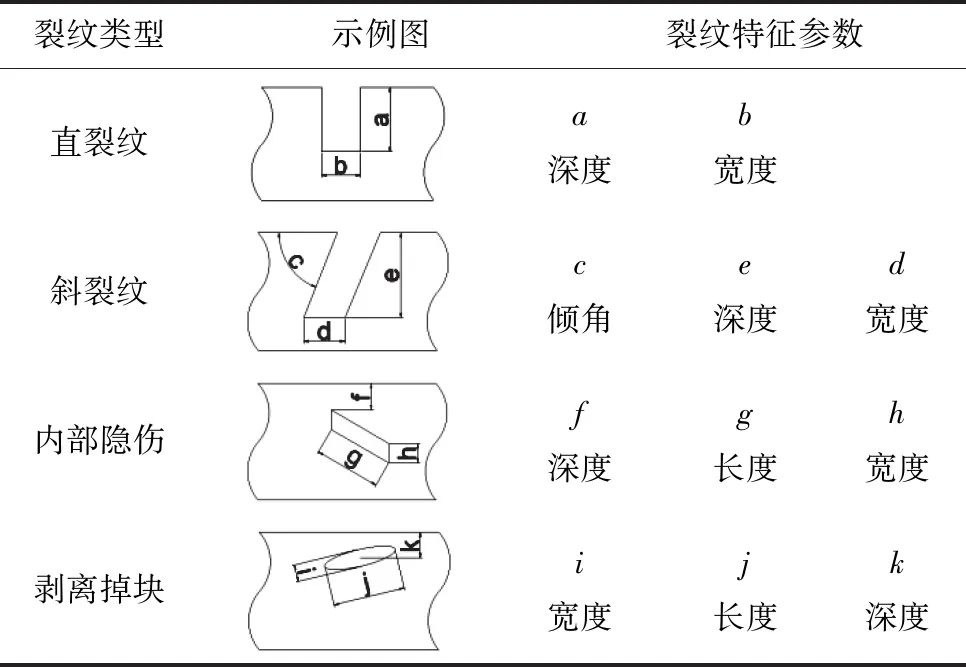
表1 钢轨RCF裂纹类型及参数

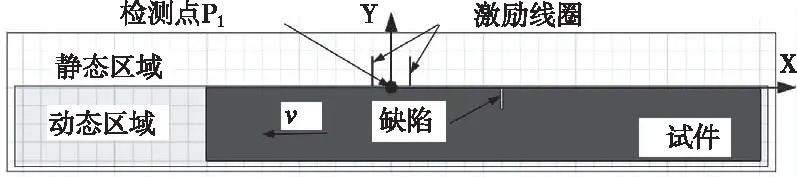
图8 动静区域划分

在该模块设计中,利用ANSYSMaxwell仿真脚本录制功能,依次完成模型建立、材料属性设置、运动设置和网格划分等功能脚本的录制。因其脚本文件不能直接用于C#编制,该模块通过修改其脚本、提取参数并设置为相应控件的输入值,从而完成脚本文件的编写过程。该模块的实现流程如图9所示。

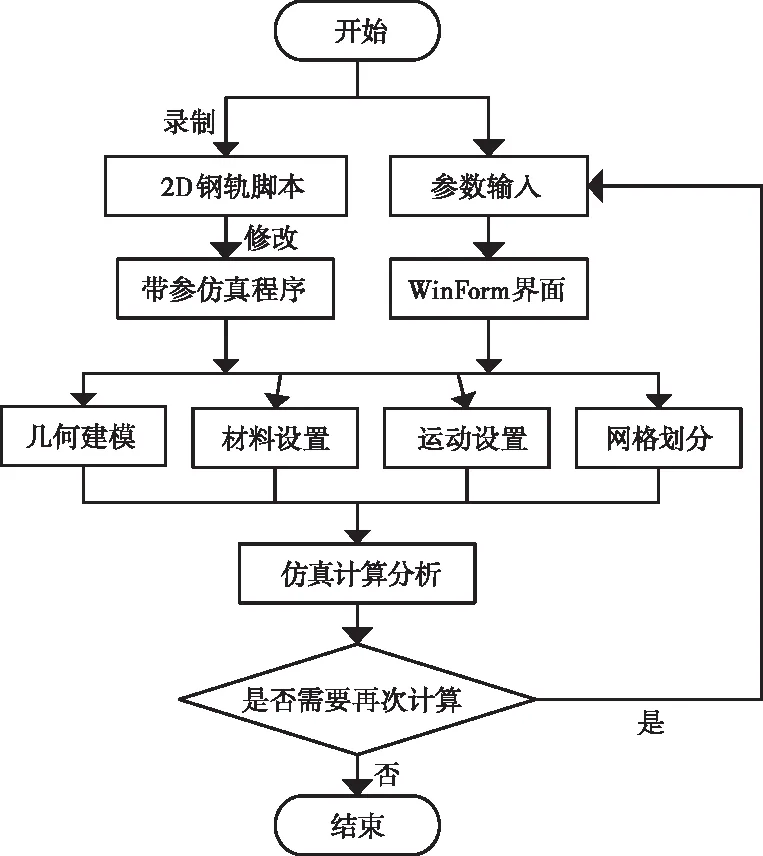
图9 2D仿真模块开发流程

3.3.3 高速钢轨RCF裂纹直流电磁无损检测3D仿真

在2D仿真平台虽然实现参数化仿真,但实际的高铁线路中钢轨具有复杂的几何结构,由轨头、轨腰、轨底构成,如图10所示。图中,WH为轨头高度;b为钢轨冠状高度;WT为轨腰高度;HF为接头夹板安装面高度;H为钢轨高度;TF为轨底边缘厚度;WF为轨底宽度。因此,2D仿真无法全面了解运动情形下含裂纹钢轨的不同视角的磁场分布,为此设计了钢轨疲劳裂纹直流电磁无损检测3D电磁场动态仿真模块。

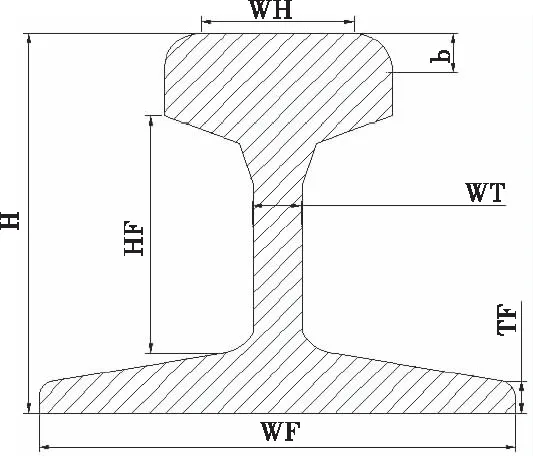
图10 高速钢轨几何结构

虽然钢轨RCF裂纹直流电磁无损检测3D仿真模块也可采用和2D仿真模块类似的方法建立。但ANSYSMaxwell中直流电磁无损检测3D仿真相比2D仿真而言,计算耗时太长(在IntelCPU为E5-2630,主频为2.40Hz,RAM为128GB的64位计算机上大概需要2个月),若要及时获取3D仿真的电磁场数据并实现数据的可视化,3.3.2小节所述的2D仿真平台的构建方法已不再适合。为此本文提出一种基于数据库的钢轨疲劳裂纹动生涡流场仿真平台构建方法。该方法分两步实现:首先建立不同的钢轨几何裂纹模型,通过ANSYSMaxwell有限元求解后,将结果数据存储于数据库中,如此循环往复,最终建立3D高速钢轨疲劳裂纹库,然后在3D仿真平台上选择不同裂纹类型跳转到相应的几何参数界面,对给定的钢轨裂纹几何参数和速度,调用3D高速钢轨疲劳裂纹库进行查询,最终将仿真结果显示于界面,开发流程如图11所示。

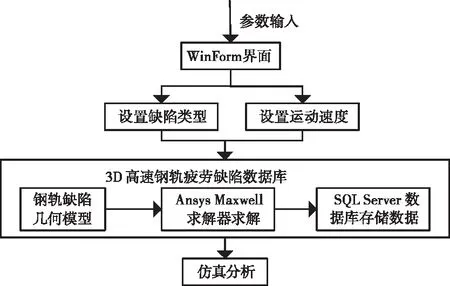
图11 三维仿真模块开发流程

在3D仿真平台构建过程中,通过查看ANSYSMaxwell的仿真文件,发现每一次仿真结果数据量非常大(>200GB),主要为仿真流程产生的数据,分别为动静态网格划分文件、磁场分布文件、仿真结果文件等,如果这些文件直接全部存储于数据库,会降低结果显示的及时性。因此通过数据获取技术,在C#程序里添加SQL查询语句,将不同速度、不同位置下的磁矢量势提取存储于数据库后,直接调用显示需要的结果数据,以此解决了存储数据量大和查询缓慢的问题。

4 仿真系统开发实例

按照上述基础理论和开发流程,以某钢轨为对象对三个模块进行实例开发。在金属构件解析计算模块中,在一定参数范围内,可根据数学模型提示输入需计算的参数裂纹参数,点击计算按钮完成计算,并将磁场计算结果存储并显示,如图12所示。钢轨疲劳裂纹无损检测2D仿真模块参照几何模型和运动模型参数化的流程建模、仿真后,通过结果显示按钮可获得仿真结果,从结果可知裂纹位置并实现对不同参数下的计算结果做对比分析,如图13所示。钢轨RCF裂纹无损检测3D仿真模块中,首先选择裂纹类型,然后输入裂纹参数、线圈参数、激励参数等,并将这些输入参数作为索引条件,通过调用数据库,将存储的数据在界面上动态显示,可实时查看不同时刻仿真结果,如图14所示。

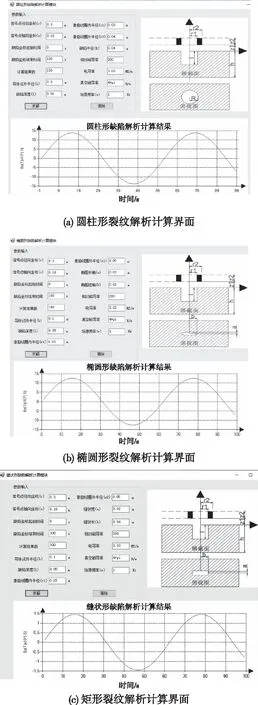
图12 金属构件解析计算模块开发实例

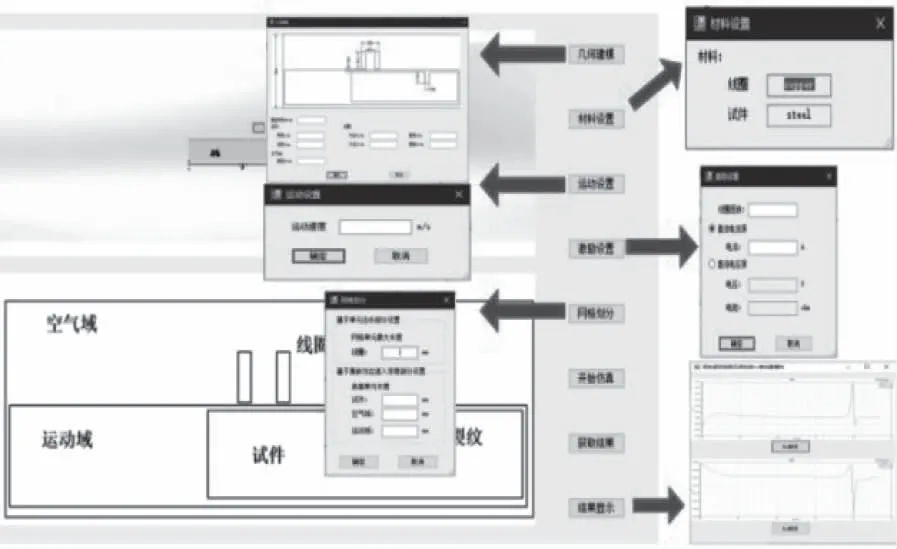
图13 钢轨RCF裂纹无损检测2D仿真模块界面

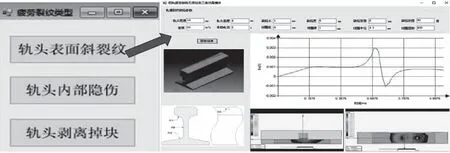
图14 钢轨RCF裂纹无损检测3D仿真模块

5 仿真系统开发实例

5.1 静态裂纹参数对电涡流磁感应强度的影响

将钢轨矩形裂纹深度设定为2mm、宽度设定为2mm时,分别设置矩形裂纹长度为2mm、4mm、6mm、8mm、10mm和12mm时,采用金属构件解析计算模块分析裂纹长度与Bz峰值的关系,如图15(a)所示。将钢轨裂纹深度设定为2mm、长度设定为2mm时,设置矩形裂纹宽度分别为2mm、4mm、6mm、8mm、10mm和12mm时,分析钢轨伤损的矩形裂纹宽度与Bz峰值的关系,如图15(b)所示。

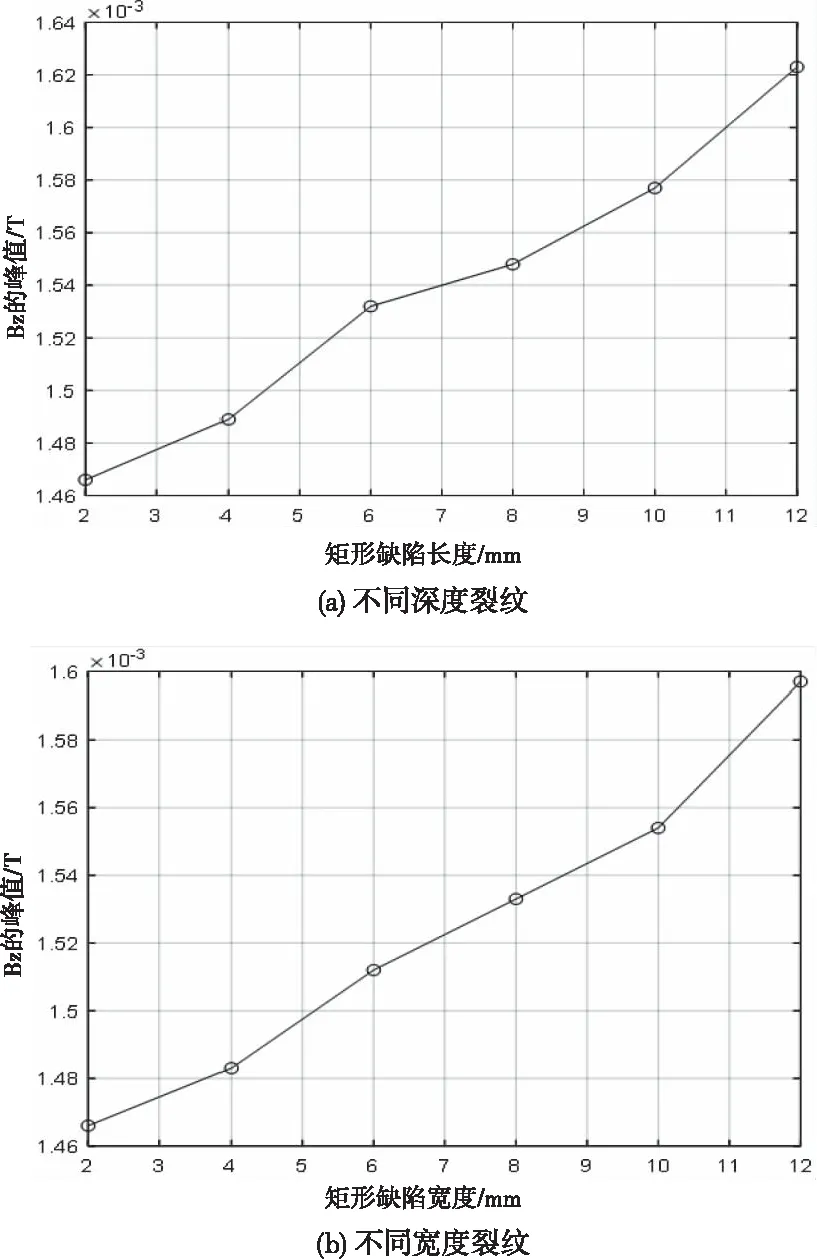
图15 矩形裂纹与Bz峰值的关系曲线

从图15(a)中可看出,当钢轨伤损中直裂纹深度为2mm、宽度为2mm时,随矩形裂纹长度增加磁感应强度Bz峰值随之增加。从图15(b)中可看出,当钢轨伤损的矩形裂纹深度为2mm、长度为2mm时,随矩形裂纹宽度增加,磁感应强度Bz的峰值也随之增加。

5.2 2D高速钢轨RCF裂纹对电涡流磁感应强度的影响

采用仿真系统中高速运行下钢轨RCF裂纹2D和3D仿真模块,可实现对动生涡流磁场分布与钢轨RCF裂纹深度与宽度的定量分析。当直流激励电压为5V,提离距离为0.5mm,线圈内径、外径和高度分别为10mm、10.5mm和8mm,线圈匝数为200匝时,得到检测速度为5m/s和20m/s时钢轨内部动生涡流分布图,如图16所示。可看出,随检测速度增加,钢轨中动生涡流越强,且趋肤效应和拖影效应越明显。

图16 动生涡流分布图

当检测速度为20m/s时,裂纹宽度为0.5mm,深度分别为1mm、2mm、4mm、5mm和6mm时,可得到P1点处(如图9所示)磁感应强度水平(X轴)分量Bx和竖直(Y轴)分量By值,裂纹深度与Bx、By关系曲线如图17所示。当裂纹深度为6mm,宽度为0.5mm、1.0mm、1.5mm和2.0mm时,同样可获取P1点处的Bx和By值,得到如图18所示裂纹宽度与磁感应强度的关系曲线。

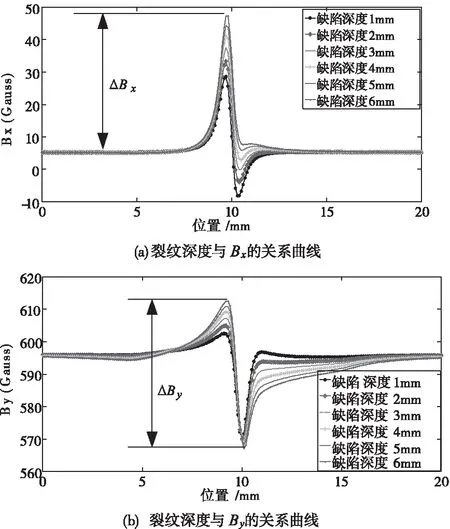
图17 不同裂纹深度与磁感应强度的关系曲线

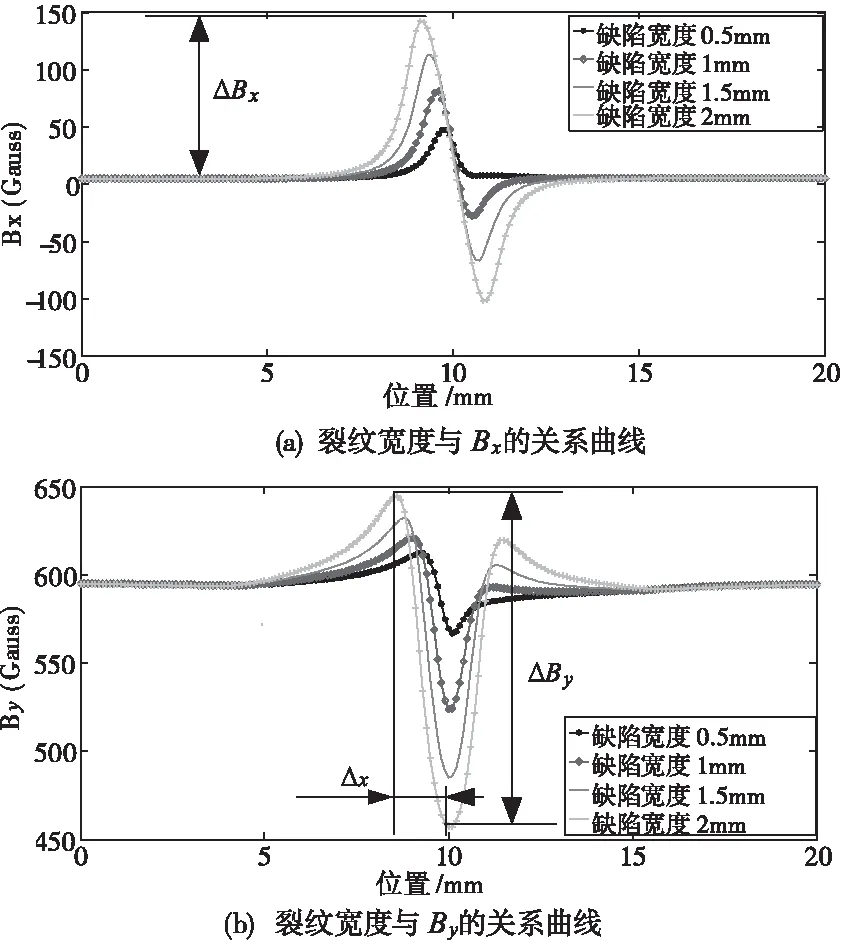
图18 不同裂纹宽度与磁感应强度的关系曲线

从图17可观察到,随裂纹深度增加,Bx峰值随之增加,而谷值逐渐减小并消失;By峰值与谷值的绝对值(即△Bx)增加。但随裂纹深度增加,By峰值和谷值的绝对值(即△By)变化趋势均减缓。因此,可通过磁感应强度Bx、By峰值和谷值对裂纹深度进行识别。从图18中同样可得出,随裂纹宽度增加,Bx和By峰值增大,By谷值的绝对值也增大。同时,如图18(b)所示,随着裂纹宽度的增加,By的峰值与谷值之间的距离△x增加。因此可通过Bx、By峰值和谷值对裂纹的深度和宽度进行识别。

5.3 3D高速钢轨RCF裂纹对电涡流磁感应强度的影响

为分析不同钢轨裂纹对磁感应强度的影响。设置巡检速度为20m/s,裂纹宽度为0.8mm,裂纹深度分别为0.5mm、1.0mm、1.5mm、2.0mm时,研究磁感应强度峰值X方向和Y方向的变化情况,其X方向、Y方向的磁感应强度的峰值随裂纹深度的变化曲线分别如图19(a)和19(b)所示。

从图19(a)的X方向磁感应强度峰值变化曲线可以看出,随着裂纹深度的增加,检测到的磁感应强度增强。从图19(b)的Y方向磁感应强度峰值变化曲线可以看出,随着裂纹深度的增加,检测到的磁感应强度增强。进一步分析对比X方向和Y方向的磁感应强度峰值的相对大小,发现X方向的磁感应强度峰值小于Y方向的磁感应强度峰值。

6 总结

本文设计开发了适用于钢轨RCF裂纹电涡流检测评估仿真系统,通过该系统可实现涡流无损检测电磁场的快速解析计算,也可对运动状态下钢轨中滚动接触疲劳裂纹的特征参数和动态电磁场的关系进行深入研究,为提出钢轨滚动接触疲劳裂纹的定量、快速无损检测方法提供支撑。此外,该系统在C#平台上联合MATLAB、ANSYSMaxwell和数据库技术,将静态电磁场的晦涩难懂的解析计算过程和动态电磁场的复杂建模过程进行封装,在降低系统的使用难度的同时,可实现含不同RCF裂纹的高速钢轨电磁场的快速计算和快速可视化。

因此该系统不仅可用于提出钢轨RCF裂纹的电涡流无损定量检测方法、正向逆向问题研究、探头优化设计和试验验证,也为进一步构建钢轨RCF裂纹的无损快速定量化检测系统对应的数字孪生系统奠定基础。