基于PCA＿HCM的UAQ影响因素及区域性研究

2023-09-21罗小玲张立倩

计算机仿真 2023年8期

刘敏,罗小玲,潘新,张立倩

(内蒙古农业大学计算机与信息工程学院,内蒙古呼和浩特 010018)

1 引言

当前,我国经济高速发展,但随之而来的是环境空气质量的下降[1-3],严重威胁人类健康,影响植物生长。《环境空气质量标准》(GB3095-2012)中规定参与环境空气质量优劣评价的主要污染物指标为SO2(二氧化硫)、N02(二氧化氮)、PM10(可吸入颗粒物)、C0(一氧化碳)、O3(臭氧)和PM2.5(细颗粒物)6项[4,5]。《环境空气质量指数(AQI)技术规定(试行)》中指出空气质量分为6个等级,6级属于严重污染,1级属于优,级别越高说明污染的情况越严重[6]。

近年来,国内外学者围绕环境空气质量的污染物指标[7-9]、预测模型[10,11]和地区差异[12,13]开展了广泛的研究,如文献[8]分析了火灾排放对地表细颗粒物浓度和空气质量的影响;文献[9]根据可吸入颗粒物、二氧化氮和臭氧对欧洲6个城市的空气污染情况进行评估;文献[10,11]基于贝叶斯模型预测和诊断城市空气质量;文献[12]研究COVID-19大流行病前后印度3个城市空气质量的差异;文献[13]采用K均值聚类法对我国113个城市的空气质量进行了区域性研究。上述文献没有结合污染物综合指标研究区域性污染,提取环境空气质量评价中的污染物综合指标既可以降低问题的复杂度,又便于环境保护部门快速了解区域性污染来源,科学制定区域性大气污染防治措施,为此,本文拟利用中国统计年鉴提供的2015-2019年全国31个主要城市环境空气质量情况的155条样本数据,采用主成分分析法(PCA)[14]研究表征环境空气质量状况的污染物综合指标,并基于综合指标结合谱系聚类法(HCM)对31个城市的环境空气质量进行分类。

2 材料与方法

2.1 数据来源

本文数据选自于《中国统计年鉴》,是关于2015年至2019年全国31个主要城市环境空气质量情况的数据,共155个样本,每个样本有9项指标,依次为:city:城市;year:年份;x1:SO2(μg/m3);x2:N02(μg/m3);x3:PM10(μg/m3);x4:C0(mg/m3);x5:O3(μg/m3);x6:PM2.5(μg/m3);y:空气质量达到及好于二级的天数(天)。使用的软件为SAS9.0,部分样本数据见表1。

表1 部分样本数据

2.2 主成分分析法

主成分分析(Principal Component Analysis)也称PCA法,是处理多个具有相关性指标的一种统计方法。该方法运用降维的思想,通过正交变换对原始指标作线性组合,获得尽可能少的互不相关的综合指标即主成分去尽可能多地反映原始指标信息[15],设有n个样品,每个样品测p项指标,原始指标观测数据阵记为X,每个观测值记为xij,i=1,2,…,n,j=1,2,…,p,计算步骤如下:

1)计算X的相关阵R

i,j=1,2,…,p

(1)

当p个原始指标取值范围彼此相差很大时,需要标准化X,记为X*,从X的相关阵出发计算主成分等价于标准化处理。

2)计算相关阵R的特征值及单位正交化特征向量

R的特征值按降序排列为:λ1≥λ2≥…λp>0,第i个主成分为Fi,λi是Fi的方差,特征值相应的正交化单位特征向量记为

X的第i个主成分为

(2)

3)选取主成分

4)解释主成分

5)计算主成分得分

计算n个样品在m个主成分上的得分

j=1,2,…,m

(3)

2.3 谱系聚类法

谱系聚类法(Hierarchical Clustering Method)也称HCM法,用来研究样品分类的一种统计方法,它的思想是用距离尺度衡量样品之间的亲疏程度并以此来实现分类[16]。设有n个样品观测值,每个观测值测p项指标(变量),得到观测数据xij,i=1,2,…,n,j=1,2,…,p,Xj=(X1j,X2j,…,Xnj)T表示第j项指标,X(i)=(Xi1,Xi2,…,Xip)表示第i个样品,基本步骤如下:

1)标准化数据

(4)

(5)

(6)

2)计算n个样品两两间的距离

可以使用明氏、兰氏或者马氏距离公式计算n个样品两两间的距离,得样品间的距离矩阵D(0)。定义样品X(i)到样品X(j)的欧氏距离为

(7)

开始每个样品自成一类,此时Dij=dij。

3)合并类间距离最小的两类为一新类

找出D(0)的非对角线最小元素,设为Dpq,则将Gp和Gq合并成一个新类Gr={Gp,Gq}。

4)计算新类Gr与其它类Gk的距离

可以使用最短距离法、类平均法、离差平方和法等方法计算新类Gr与其它类Gk的距离,以类平均法为例定义

(8)

将D(0)中第p、q行及p、q列合并成新行新列,新行新列对应Gr,此时距离阵记为D(1)。

5)对D(1)重复2)、3)两步得D(2),如此下去,直到所有的元素并成一类为止。

6)绘制谱系聚类图

以每一步合并类的最小类间距离为横轴,样品序号为纵轴,绘制横向聚类图,从聚类图上可以清晰地描述各个类的样本点。

7)决定分类个数及各类样本点

伪F统计量用于评价分为k个类的效果,设已将n个样品分为k类。

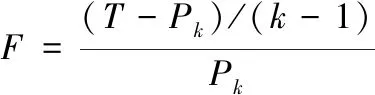
(9)

其中Pk为分类数为k个类时的总类内离差平方和,T为所有样品或变量的总离差平方和,取伪F统计量较大而类数较小的聚类水平。

3 结果与分析

3.1 不同时期环境空气质量差异的方差分析

双因素方差分析模型中选取y(空气质量达到及好于二级的天数)为观测值,year(年份)和city(城市)为因素A和因素B,这里主要分析因素A(year)对y的作用是否显著,对于因素A(year)的显著性F检验结果中,FA=10.85,p<0.0001,在0.05的显著性水平下,因素A的作用显著,说明2015年到2019年间31个城市环境空气质量有显著差异,接下来使用邓肯法进一步做组间多重比较,比较结果见表2。

表2 邓肯法组间多重比较结果

由表2可知,2019年31个城市空气质量达到及好于二级的平均天数为284天,环境空气质量与2015年至2018年显著不同,是这5年中空气质量最优的,2018年次之,2015年最差,这说明全国环境空气质量逐渐改善,呈持续向好局面,这得益于全国各地各部门积极优化产业布局,节能减排,推进煤炭清洁化利用等一系列对大气污染联防联控的措施。

3.2 使用PCA法分析环境空气质量污染物综合指标

基于方差分析的结论,PCA法选取了2019年全国31个主要城市环境空气质量的数据,样本数为31个,指标为6项,分别是x1-x6(即SO2、N02、PM10、C0、O3、PM2.5)。

1)标准化数据

由表1可知,样本数据6项指标取值范围彼此相差大,所以首先利用式(6)对样本数据进行标准化,标准化后的部分数据见表3。

2)计算相关阵R

为了验证6项污染物指标的相关性,需要利用式(1)计算原始指标pearson相关阵R,计算结果如下

根据相关阵R可知SO2(x1)与C0(x4)相关性最强,相关系数为0.66411;N02(x2)与PM10(x3)、PM2.5(x6)相关性最强,相关系数为0.76444和0.76980;PM10(x3)与PM2.5(x6)相关性最强,相关系数为0.91405,指标之间存在一定的相关性。

3)计算相关阵R特征值和特征向量

从相关阵R出发,计算特征值和特征向量,并进一步找到主成分。相关阵R的特征值和主成分贡献率见表4。

表4 相关阵的特征值和主成分贡献率

由表4可知,第一、第二主成分的贡献率分别为63.59%和21.25%,累积贡献率为84.83%。

4)选取并解释主成分

按照累积贡献率达到85%的原则,本文选取前2个主成分,这2个主成分可以反映原始指标84.84%的信息量,约等于85%。前2个主成分的特征向量见表5。

表5 前2个主成分的特征向量

由表5及式(2)可以写出主成分的表达式如下(保留3位小数):

在第一主成分F1中,x2、x3和x6的系数绝对值是最大的前三项,分别是0.446、0.491和0.466,因此F1主要综合了N02、PM10和PM2.53项污染物指标,PM10主要来自燃煤排放的烟尘、建筑工地和地面扬起的灰尘等一次污染物,PM2.5主要来自二次颗粒物[17],可以把F1称为颗粒物污染综合指标,它能反映原始指标63.59%的信息量;在第二主成分F2中,x1、x4和x5的系数绝对值分别是0.631、0.464和0.569,因此F2主要综合了SO2、C0和O33项污染物指标,二氧化硫主要来自燃烧废气,氮氧化物主要来自汽车尾气[18],可以把F2称为废气污染综合指标,它能反映原始指标21.25%的信息量。

5)计算主成分得分并绘制主成分散点图

将31个城市的6项污染物指标的观测数据标准化后分别代入两个主成分表达式,利用式(3)计算每个城市的主成分得分并按降序输出,输出结果见表6。

表6 部分主成分得分降序排列结果

由表6可知,石家庄、太原、济南、郑州和西安这5个城市主成分得分较高,排在前5名,说明这5个城市颗粒物和废气污染较严重;昆明、贵阳、福州、海口和拉萨这5个城市主成分得分较低,空气质量好。以第一主成分为纵轴,第二主成分为横轴,绘制31个城市的主成分得分散点图,如图1所示。

图1 31个城市主成分得分散点图

从图1可以看出来,散点图越靠左上角的地区,颗粒物污染越严重(以下结论给出的城市名称均按污染程度递减排序),如颗粒物污染最严重的城市有6个,分别是石家庄、太原、济南、郑州、西安和天津;较严重的城市有12个,分别是武汉、南京、北京、合肥、杭州、成都、长沙、广州、重庆、南昌、长春和上海;较轻的城市6个,分别是南宁、昆明、贵阳、福州、海口和拉萨。越靠右侧的地区,废气污染越严重,废气污染较严重的7个城市有西宁、兰州、沈阳、哈尔滨、呼和浩特、银川和乌鲁木齐。越靠右上角的地区,颗粒物废气污染越严重,相对来说,石家庄和太原这两个城市环境空气质量较差。越靠左下角的地区,颗粒物废气污染越少,环境空气质量越好,相较于其它城市,福州和海口的环境更宜人。

3.3 使用HCM法基于污染物综合指标进行聚类分析

根据前2个主成分对2019年31个城市的环境空气质量数据进行主成分聚类分析,聚类历史的输出结果见表7,在类别控制在4类以下的前提下,利用式(9)计算的伪F统计量最大和次大依次为49.4和24.5,建议分为4类或3类是较合适的;伪T2最大和次大依次为47和21,建议分为4类或2类;半偏R2最大和次大依次为0.4199和0.2162,建议分为2类或3类;R2最大和次大依次为0.846和0.636,建立分为4类或3类,综合以上统计量及主成分得分的信息,最终决定分为4类能较准确地体现城市环境空气质量的区域特性,分类结果如图2所示。

图2 31个城市类平均法横向聚类图

表7 聚类历史输出结果

在图2的聚类图上进行标识,可以看出,第一类城市群有{济南、天津、西安、郑州、石家庄、太原};第二类城市群有{哈尔滨、银川、西宁、呼和浩特、沈阳、乌鲁木齐、兰州};第三类城市群有{北京、成都、杭州、合肥、广州、长沙、重庆、南京、武汉、南昌、长春、上海};第四类城市群有{福州、海口、拉萨、贵阳、昆明、南宁},与主成分得分的散点图分析结论一致。综合比较而言,第一类城市群是大气污染的重灾区[19],这些地区在京津冀周边,属于我国内陆城市,沙尘天气多,城市大风日数较少,不利于污染物扩散,冬季通过燃煤取暖,产业结构以重工业为主,复合型大气污染比较突出,尤其是石家庄和太原两个城市,颗粒物和废弃污染问题严峻。第二类城市群大部分位于我国的西北部,气候干燥,春秋风沙大,虽然能源结构也是以煤炭为主,但是相较于前两类城市群,经济欠发达,地广人稀,汽车保有量逐年增加,目前亟需解决的是废气污染。第三类城市群中大部分城市属于长三角区域,处于我国南方,常年雨水多,对空气污染能起到一定减少的作用,但是这些地区土地面积狭小,资源消耗大,人类活动强度高,目前主要面临颗粒物污染[20]。第四类城市群环境宜人,有的城市依江面海,自然植被密集,有的城市海拔高,全年日照时间长,人口密度低,这些都有利于形成优良的城市环境空气质量。

4 结论

本文采用双因素无交互作用的方差分析法、主成分分析法(PCA)和谱系聚类法(HCM)探讨了2015-2019这五年不同时期全国环境空气质量的总体差异、影响环境空气质量的污染物综合指标以及城市环境空气质量的区域性特征,结果表明:

1)2019年全国空气质量达到及好于二级的平均天数为284天,与2015年-2018年显著不同,环境空气质量最优;2018年与2016年、2015年与2017年的环境空气质量无差异;2015年环境空气质量最差。

2)影响环境空气质量污染物的6项原始指标之间具有不同程度的相关性,经过PCA法获得了颗粒物和废气2个主成分,分别提取原始指标63.59%和21.25%的信息量,累积提取原始指标约85%的信息量;

3)基于颗粒物和废气2个主成分,使用HCM法对31个城市环境空气质量由好至差分为了4类,第一类城市群有{济南、天津、西安、郑州、石家庄、太原};第二类城市群有{哈尔滨、银川、西宁、呼和浩特、沈阳、乌鲁木齐、兰州};第三类城市群有{北京、成都、杭州、合肥、广州、长沙、重庆、南京、武汉、南昌、长春、上海};第四类城市群有{福州、海口、拉萨、贵阳、昆明、南宁}。