CRH3C 型高速动车车辆振动及平稳性分析

吴舟，赵建新，王自立，陈冬丽

（455000 河南省 安阳市 安阳职业技术学院）

0 引言

铁路运输是我国主要的运输方式，不论是客车还是货运列车都在我国国民经济中起着举足轻重的作用。21 世纪中国铁路已经跨入以“高速客运、重载货运”为特征的新时代[1]。同时人们的出行方式发生了很大改变，交通工具的种类也变得多种多样。近些年高铁动车由于其费用低、速度较快，成为很多人出行交通工具的首选。列车在铁路上运行时，由于轨道不是绝对平直和绝对刚性的，有各种形式的不平顺存在，而实际的车轮也不是标准圆形，因此轮轨之间会有不同的且不断变化的相互作用力，这会引起车辆振动，对车辆运行的平稳性、乘坐舒适性和安全性以及货物的完整性造成影响[2]。

高铁的平稳运行离不开严格控制列车运行的三大指标，即纵向稳定性、横向稳定性和垂向稳定性。不论是车体还是转向架，都在运行的过程中面临着非常严峻的振动问题。本文的研究对象是京津线上速度为300～350 km/h 的CRH3C 型高速动车，从自由振动开始，对车辆的振动系统建模，分析车辆系统的有阻尼自由振动以及有阻尼的强迫振动。通过ADAMS 进行仿真，得到车辆振动相关参数，并依照国内外相关标准进行校核。

1 车辆系统动力学模型建立

车辆建模所需的主要参数如表1 所示[3]。

表1 建模主要参数Tab.1 Main modeling parameters

经过ADAMS 建模后14 个自由度的模型整体的效果图如图1 所示。

图1 车辆整体模型效果图Fig.1 Effect drawing of overall vehicle model

2 车辆系统有阻尼自由振动

2.1 车辆系统有阻尼自由振动系统建模

有阻尼自由振动系统模型如图2 所示，在车体和转向架之间增加了垂向阻尼器以模拟真实情况。阻尼器的作用是在车辆振动过程中将车辆的振动动能转化为内能消耗，使车体快速从振动状态稳定下来，提高列车运行舒适度[4]。在实际的轨道车辆中，车辆系统的一系部位具有垂向阻尼器，二系部位没有阻尼，而是靠空气弹簧的作用实现阻尼减震作用。

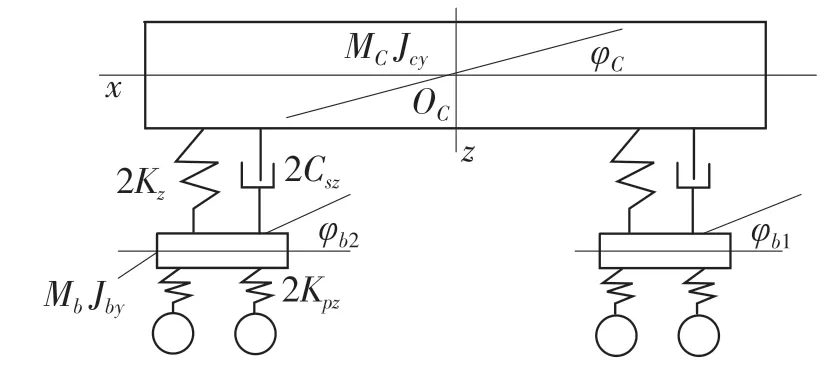
图2 有阻尼自由振系统模型Fig.2 Model of damped free vibration system

该振动系统的动力学方程为

式中：z1——前后转向架构架平均垂向位移，z1=(zb1+zb2)/2；z2——前后转向架构架垂向位移差之半，z2=(zb2-zb1)/2。

2.2 车辆有阻尼自由振动仿真及规律

（1）MATLAB 仿真

对建立的模型求解微分方程可得如下规律：由欧拉公式eipt=cospt+isinpt解得

式中：β1，β2——相位角。

式（2）说明车体和转向架的有阻尼自由振动仍然是2 种振动形式的叠加，同时高频振动和低频振动的峰值都随着幂函数衰减。相比之下，高频振动衰减的速度更快。实际的衰减过程如图3 所示。

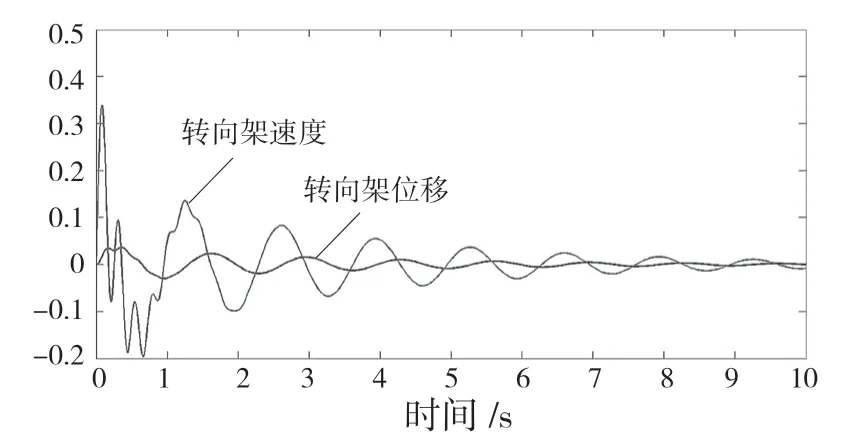
图3 有阻尼自由振动转向架位移及速度曲线Fig.3 Displacement and speed curve of damped free vibration bogie

（2）ADAMS 仿真

为了进一验证实际车辆模型的有阻尼振动过程，对模型进行动力学仿真，仿真是在车辆悬挂系统均添加相应的阻尼之后进行的，结果如图4 所示。

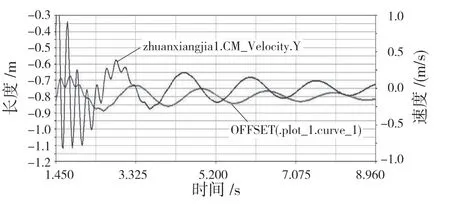
图4 有阻尼自由振动软件仿真曲线Fig.4 Software simulation curve of damped free vibration

仿真结果也验证了上文结论，即车辆有阻尼自由振动的衰减曲线仍然是由2 种频率的自由振动曲线叠加而成，高频震动叠加在低频振动上。同时2 种频率的振动在同时衰减，直到最后趋于稳定，这样就可以使车辆迅速稳定下来。

3 车辆系统有阻尼强迫振动及平稳性分析

3.1 有阻尼强迫振动系统动力学建模

有阻尼强迫振动模型的理论研究相对复杂，本文只进行简单的动力学方程的建立，未做具体的理论分析，主要采用ADAMS 建模，对车辆施加特定的轨道激扰力，以研究其振动响应以及车辆运行平稳性的相关指标。车辆有阻尼强迫振动的简化模型如图5 所示。

图5 有阻尼强迫振动系统简化模型Fig.5 Simplified model of damped forced vibration system

设线路的波形为Zi=asinωt[5]，则两系悬挂车辆的强迫振动方程为

式中：β1——第2 轮对落后于第1 轮对的相位角，β1=4πl1/Lr；β2——第3 轮对落后于第1 轮对的相位角，β2=4πl/Lr；β3——第4 轮对落后于第1 轮对的相位角，其值为β3=4π(l1+l)/Lr；Lr——轨道不平顺波长；l1——转向架轴距之半；l——车辆定距之半。

由式（3）可知，悬挂系统垂向振动可分为以下几组独立的振动：（1）车体浮沉振动与转向架浮沉平均值耦合的强迫振动；（2）车体的点头与转向架浮沉差耦合的强迫振动；（3）车体前后2 组转向架各自做单自由度的受迫振动。

3.2 有阻尼强迫振动系统动力学仿真及平稳性分析

通过ADAMS 动力学仿真计算并验证车辆的舒适度指标，主要验证Sperling 指标以及车体横向垂向加速度。

当垂向激扰为y=0.008×sin（8×PI×time），横向激扰为z=0.006×sin（8×PI×time）时，经ADAMS 仿真后，得到的车体垂向横向加速度分别如图6、图7 所示。

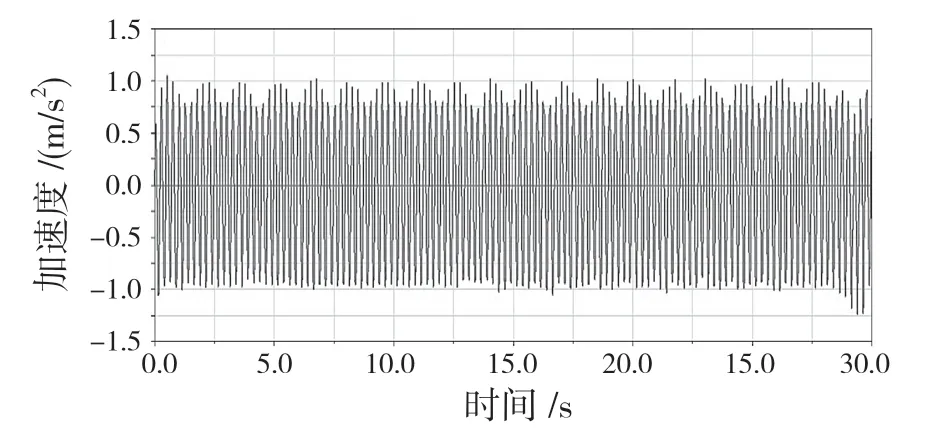
图6 车体垂向加速度Fig.6 Vertical acceleration of vehicle body

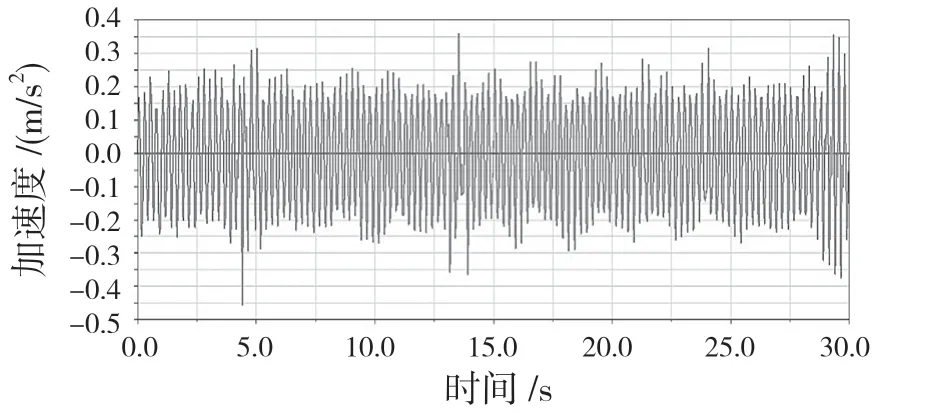
图7 车体横向加速度Fig.7 Lateral acceleration of vehicle body

（1）车体垂向、横向加速度。由图6、图7可以看出，车体垂向加速度在[-1，1]之内，而横向加速度在[-0.4，0.35]之内。根据国际铁路联盟UIC-518 标准对运行品质的评价规定中，要求垂向及横向加速度值都应小于等于2.5 m/s2，即y≤2.5 m/s2。对比发现，车体加速度小于规定限值，故在此状态下车体的平稳性是可靠的，是合格的。

（2）Sperling 指标[6]。用平稳性指标评价车辆运行性能的方法在国际上获得广泛应用。Sperling平稳性指标是基于大量实验制定的平稳性指标，用于评定车辆本身的运行品质和旅客乘坐舒适性，认为运行品质由车辆本身衡量，舒适度还与乘客对周围振动环境的敏感度有关系。

我国制定的GB 5599-1985《机车车辆动力学性能评定及试验鉴定规范》基本上与Sperling 平稳性指标评价方法相同[7]。对于数据的后处理，GB 5599-1985 推荐如下计算步骤：（1）将测试数据经A/D 转换并计算，得到用实际物理量表示的离散数据；（2）将得到的数据进行FFT 变换并计算其频谱；（3）对振动频率为20 Hz 以下的所有频率进行计算，求出平稳性指标W。

由于Sperling 指标是针对舒适度的，因此横向和垂向舒适度指标都可以用Sperling 指标来表征。将车体垂向加速度曲线经FFT 变换[8]得到加速度随频率的变化曲线，如图8 所示。

图8 加速度随频率的变化曲线Fig.8 Acceleration versus frequency curve

由图8 可知，当f=1 Hz 及f=4 Hz 时，加速度出现极大值。根据Sperling 指标的计算公式可得

当f=1 Hz 时

当f=4 Hz 时

将2 种频率的W合成为

由W的值可以发现，虽然W是由W1和W2合成，但是W的值受W2的影响最大，受W1的影响微乎其微。所以在合成W时，并不需要代入很多的点去计算，因为其他点算得的W值比W1更小，对合成W的值影响可以忽略不计。所以，对比平稳性指标评定参考值可知，2.75＜Spering 指标值＜3，平稳等级为3 级，评定为合格。

综合Sperling 指标和横向、垂向加速度的值，车体都是处于平稳状态，即振动较小，对人的影响在可接受范围内。

4 结语

针对当前快速发展的高铁动车，提出列车行车平稳运行参数化的评价体系。首先运用ADAMS 软件、以CRH3C 型号的动车组为参考建立整体为14个自由度的车辆系统振动模型；其次，在车辆振动性研究方面，从有阻尼自由振动系统研究开始，建立理论力学模型，利用MATLAB 软件进行微分方程的建立与求解，运用数学方法对车辆系统的振动性进行分析；最后，参照Sperling 及车体横向垂向加速度值等指标，通过ADAMS 的动力学仿真对车辆运行的平稳性进行了综合分析与对照验证，为今后展开该方面的研究提供了数据参考和理论支撑。