基于新型趋近律的PMSM 模糊自适应积分滑模控制

李虎，刘泓滨

（650500 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

近年来，永磁同步电机（PMSM）凭借结构简单、输出效率高和散热快等优势被广泛应用于数控机床、航空航天以及机器人等领域。但由于PMSM是一种多变量和强耦合的非线性复杂系统，当电机受到负载干扰或参数发生改变时，系统性能无法得到有效保证。因此，所设计的各种控制器必须具有很好的稳定性以及抗负载能力。目前，常用的PMSM 调速控制策略主要有PI 控制、自适应控制、滑模变结构控制以及其他的智能控制算法。甘志涵等[1]采用传统的PI 控制算法对PMSM 进行调速，虽然PI 控制器结构简单、便于实现，但是这种控制方法很容易受到外部干扰和电机参数变化的影响，很难得到理想的控制结果；任金霞等[2]研究了模型参考自适应控制在PMSM 中的应用，当电机负载发生突变时，模型参考自适应控制效果不理想；樊英杰等[3]采用模糊PI 控制算法对PMSM 的矢量系统进行优化，由于模糊推理规则库是由专家经验规定的，所以模糊PI 控制也难以达到预期效果；张苏英等[4]基于趋近律设计了滑模变结构控制算法，这种控制算法受外界干扰以及电机参数变化的影响较小，所以具有较好的鲁棒性，但在电机控制过程中存在抖振现象，因此削弱抖振是滑模控制中需要解决的首要问题。为了克服滑模控制存在的抖振和控制精度不高的问题，很多学者进行了深入研究，并取得了大量成果。王要强等[5]、闫宏亮等[6]、郭小定等[7]对传统趋近律进行了改进，研究结果表明,新型趋近律可有效削弱系统的抖振并提高系统收敛速度。张攀等[8]结合新型趋近律设计了一种滑模控制器，在控制器中引入双曲正切函数，改善了系统抖振。

总结上述经验，本文将模糊控制和积分滑模控制相结合，设计了一种具有积分滑模面和参数自适应的滑模变结构控制器。为了研究该控制器在PMSM 速度调节系统中的控制效果，在MATLAB/Simulink 中搭建PMSM 调速系统的仿真模型并进行仿真分析，比较分析模糊自适应积分滑模控制系统与指数趋近率的滑模控制和PI 控制系统在电机负载时转速、三相电流以及电机电磁转矩的变化。

1 PMSM 的数学模型

PMSM在同步旋转坐标系d-q下的电压方程[9]为

电机磁链方程为

将式（2）代入式（1）得电机定子电压方程为

电机电磁转矩方程为

由于表贴式PMSM的d-q轴电感相等，所以转矩方程为

电机的机械运动方程为

式中：ud，uq——d-q的电压；id，iq——d-q的电流；Ld，Lq——d-q的电感；R——定子电阻；Pn——极对数；φd，φq——d-q的磁链；φf——磁链；Te——电磁转矩；TL——电机负载转矩；J——转动惯量；we——电角速度；w——机械角速度。

2 滑模变结构控制

2.1 积分型滑模面控制

常用的滑模面函数中包含转速误差的微分项，极易产生噪声以及受外部干扰导致系统抖振[10]。本文设计了积分型滑模面函数，不考虑电机转速误差的导数项。积分型滑模面可以使转矩平滑输出，有效削弱系统抖振。

滑模控制器为了保证给定转速wr和实际转速w的跟踪误差最小，定义系统的状态变量为

式中：e（t）——电机转速跟踪误差；wr——电机给定转速；w——实际转速。

选取的积分型滑模面函数为

式中：c——常数，c＞0。

对s求微分，由式（5）—式（8）可得：

2.2 趋近律的设计

采用趋近律的滑模控制算法可以有效削弱系统抖振。对PMSM 而言，常用趋近律有指数趋近律和幂次趋近律等，为提高电机的运行性能，本文结合指数趋近律和幂次趋近律提出的新型趋近律为

式中：ε＞ 0；k＞ 0；0 ＜α＜ 1；=-ks是指数项，其解为s=s（0）e-kt。

可见指数收敛至0，收敛速度取决于k值，指数项-ks能保证当s 较大时，系统状态能以较大的速度趋近于滑动模态；通过调整α值，可保证当系统状态远离滑动模态时，能快速趋近于滑动模态；当系统状态趋近滑动模态时，保证较小的控制增益，以降低抖振。

2.3 控制量的设计

由式（9）和式（11）可得

整理式（10）—式（12）得滑模控制器的控制量iq的表达式

在滑模变结构控制系统中，符号函数为不连续函数，是造成系统抖振的原因之一。为进一步减弱系统抖振，本文利用饱和函数代替符号函数[12]。饱和函数的表达式为

式中：σ——边界层。

由式（13）和式（14）整理得控制量为

稳定性验证：取Lyapunov 函数为V（x）=s2/2，对其求微分得

3 模糊自适应积分滑模控制器（FASMC）

PMSM 调速系统采用传统趋近律的滑模变结构控制器时，因电机内部参数和外部干扰的变化，很容易影响电机的动态性能，不能保证系统的稳定性，所以采用模糊控制调节新型趋近律的参数，当电机运转中受到外界干扰和内部参数发生改变时，可以在线自整定新型趋近律中的参数，提高系统的抗干扰能力和稳定性。

FASMC 主要由模糊控制器和积分滑模控制器组成。模糊控制器的输入为转速的误差E和误差变化率Ec，输出为滑模控制器中参数的修正值Δk、Δα，实现滑模控制器的实时整定。FASMC算法架构如图1 所示。

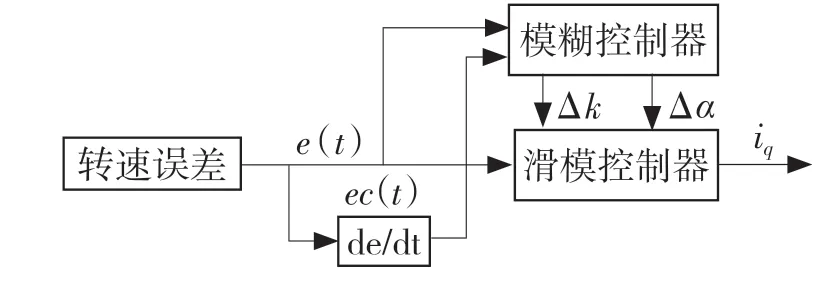
图1 FASMC 原理框图Fig.1 Schematic diagram of FASMC

则模糊自适应积分滑模控制器的参数为

式中：k、α——修正后的积分滑模控制器的参数；k1、α1——电机在未启动前参数的初始值；Δk、Δα——模糊控制根据电机运行时参数实时修正的滑模控制器参数的变化量。

在模糊逻辑控制中最重要的3 个步骤：（1）确定模糊控制器中输入输出变量的模糊集合和论域；（2）确定模糊控制器中输入输出的隶属度函数和根据专家经验得出的模糊控制规则库；（3）将输入的清晰量进行模糊化和输出的模糊量进行逆模糊化。在本文中输入和输出变量的模糊集为{负大（NB），负中（NM），负小 (NS)，零（ZE），正小（PS）,正中（PM），正大（PB）}；论域取值为：E∈[-3 3]，Ec∈[-3 3]，k∈[-3 3]，α∈[0 1]，其中模糊化的量化因子的计算和确定参考李晓丹[12]的研究。在模糊控制中2 个模糊集的隶属度函数曲线交点的值过大会导致控制系统的灵敏度降低，过小则影响控制系统的稳定性，因此该FASMC 选用三角形隶属度函数，输入和输出变量隶属度函数曲线如图2 所示。

图2 隶属度函数Fig.2 Membership function

模糊化的输入变量经过模糊推理运算得到模糊的输出变量，对模糊输出量进行逆模糊化。本文采用重心法进行逆模糊化求解，重心法的表达式为

式中：μ——逆模糊化后的清晰量；μi——各组元素的权重。

根据专家经验和实验试凑法确定模糊控制中输出变量的模糊规则表，如表1 和表2 所示。

表1 Δα 的模糊控制规则表Tab.1 Fuzzy control rules of Δα

表2 Δk 的模糊控制规则表Tab.2 Fuzzy control rules of Δk

4 MATLAB 仿真与分析

为了验证FASMC 是否能够更好地削弱电机空载运行以及电机施加负载时系统的抖振，在MATLAB 中分别对PI、SMC 以及FASMC 进行了仿真对比研究，仿真时电流环调节均采用PI 控制器且参数相同，电机速度环控制采用3 种不同的控制器[13]。仿真系统中对PMSM 的参数设置如表3 所示。

表3 永磁同步电机的参数Tab.3 Parameters of PMSM

仿真条件设置为：直流侧电压Udc=311 V，PWM 开关频率设置为10 kHz，采样周期Ts=10 μs，仿真时间为0.4 s。给定转速为wr=1 000 r/min，初始负载转矩为0，在0.2 s 时负载转矩TL=10 N·m。3种控制器参数设置如下：电流环PI 控制器参数，KP=16.4，Ki=5 750；转速环PI 控制器参数，KP=8，Ki=0.05；指数趋近律的滑模控制器参数，k=300，ε=200；FASMC 的初始参数：A=1 400，B=13 333，k1=0.01，ε=1，α1=0.5，σ=10，c=3 000。

图3 为电机在PI 控制器、传统滑模控制器和FASMC 下由启动到施加负载时的转速变化曲线。图4 是在3 种控制器下电机电磁转矩的变化曲线。图5 是在3 种控制器下电机变负载时三相电流的响应曲线。由图3 可以看出，基于FASMC 可以使电机的转速迅速到达给定值，并在0.02 s 达到稳定，而其他2 种控制器则是在0.07 s 和0.032 s 时系统达到稳定而且有较大的超调量。在0.2 s 时电机增加负载时，PI 控制器和SMC 控制器的电机转速影响较大，分别在0.22 s 和0.25 s 再次达到稳定，这说明FASMC 控制器有较强的抗干扰能力和鲁棒性。

图3 3 种控制器下变化负载时电机转速变化曲线Fig.3 Motor speed curve under three controllers with varying load

图4 3 种控制器下电磁转矩变化曲线Fig.4 Variation curves of electromagnetic torque under three controllers

图5 3 种控制器下三相电流的响应曲线Fig.5 Response curves of three-phase currents under three controllers

由图4 可知，PI 控制器在电机启动时有较大的超调量且在有干扰时电磁转矩波动较大。虽然SMC 控制器没有较大的超调量，但是电机达到稳定的时间过长，在电机增加负载时电磁转矩受影响较大；FASMC 控制器相比其余2 种控制器没有较大的超调量，且受电机负载干扰的影响较小。

由图5 电机的三相电流响应波形可知，FASMC 控制器与PI 控制相比没有较大的超调量，且受电机负载干扰较小，与SMC 控制器相比可以快速地使系统达到稳定。从电机转速、电磁转矩和三相电流的变化可以看出，FASMC 可以有效地削弱系统抖振，增强系统的抗负载干扰能力和鲁棒性。

5 结论

（1）本文提出一种基于新型趋近律模糊自适应积分滑模控制方法。首先，采用新型趋近律设计系统的滑模控制器；其次，采用饱和函数代替趋近律中的符号函数；最后，采用模糊规则控制对趋近律中的参数进行在线补偿。

（2）仿真结果表明，与传统趋近律的滑模控制和PI 控制策略相比，该控制器不仅能够有效削弱系统的抖振，而且还可以提高系统的响应速度和增强系统的抗干扰能力，同时也验证了模糊自适应积分滑模控制策略的正确性和有效性。

本文只考虑了控制方法和参数对永磁同步电机的影响，未考虑外界干扰对电机动态性能的影响。今后将进一步研究外界干扰如何影响电机的动态性能和如何对外界干扰进行补偿。