七自由度冗余机械臂运动学和动力学分析及仿真

张泽玺，熊根良，张华，许宝阳，包俊阳

（201620 上海市 上海工程技术大学 上海市大型构件智能制造机器人技术协同创新中心）

0 引言

串联机械臂在工业领域逐渐大放异彩，特别是以六自由度机械臂为代表的非冗余机械臂技术已渐趋成熟。随着工业技术的高速发展，机械臂的工作场景变得愈加复杂，人们对机械臂的工作性能也有了更高的要求。传统的低自由度非冗余机械臂渐渐难以胜任，因此需要加强对以七自由度机械臂为代表的冗余机械臂的研究。冗余机械臂最大的优势在于其具有多余的自由度，因而相较于非冗余机械臂有着更高的灵活性、容错性与可靠性，且利用其自运动的特性可以实现避障[1]、避奇异点[2]、避免关节限位、优化关节力矩[3]、适应人类动作[4]等性能指标，但随着机械臂的自由度数目的增加，机械臂的运动学与动力学求解的难度也随之提高[5]，因此对冗余机械臂进行深入的研究是非常必要的。

国内外学者对七自由度冗余机械臂的运动学及动力学研究取得许多进展。Shimizu 等[6]对七自由度机械臂进行逆运动学研究，证明将臂形角作为冗余参数可完全反应机械臂的冗余性，该方法的几何意义明显，缺点在于其普适性低，仅适用于机械臂肩部和腕部均为等效球关节的构型；赵京等[7]基于臂形角参数化方法，以最小势能指标为理论依据可以确定机械臂唯一的肘部位置，继而完成了七自由度机械臂的逆运动学求解；徐俊虎等[8]对“骨科手术辅助机器人系统”中的无偏置七自由度冗余机械臂进行运动学逆解时，提出了一种以减小最大关节位移为控制优化目标的优化方法，利用该方法可显著提升机械臂的作业效率；祖迪等[9]将梯度投影法与关节角参数化方法相结合求解冗余机械臂的逆运动学问题，在梯度投影法得到一个优化近似解的基础上，再利用关节角参数化方法得到一个更为精确的解；Fei 等[10]提出将加权最小范数法与梯度投影法相结合的思路，与仅使用加权最小范数法相比，关节速度变化更加平稳，求解更加可靠；冯玉倩等[11]基于拉格朗日方法对七轴机械臂进行动力学分析与仿真，验证了其建立模型的合理性，但其不足在于仿真没有建立在实际工况环境中；刘壮壮[12]采用牛顿-欧拉方法对冗余机械臂进行了动力学求解及仿真，并基于惯性椭球原理对机械臂的动力学性能进行了分析；陈罡等[13]基于ADAMS 与MATLAB 对七自由度机械臂进行联合仿真，分析了各关节之间控制参数的耦合性，仿真结果验证了机械臂末端执行器的动态响应可以满足实际工况的需求。

本文针对七自由度机械臂Diana V2 的运动学及动力学建模的正确性问题分别进行分析与验证。针对运动学问题，首先基于D-H 方法建立机械臂的正运动学模型，再采用梯度投影法对机械臂的逆运动学问题进行求解，利用MATLAB 机器人工具箱验证结果；针对动力学问题，在SolidWorks中建立该冗余机械臂的三维模型，采用拉格朗日方法对其进行动力学理论建模，然后将模型导入ADAMS 中，将机械臂按照规划路径进行运动，得出机械臂七个关节力矩随时间变化的仿真曲线，并将仿真得到的输出信息作为MATLAB 中动力学方程的输入，MATLAB 数值分析后绘制出的力矩曲线与ADAMS 仿真曲线进行对比，以验证动力学模型的可靠性。

1 七自由度机械臂构型分析

冗余机械臂最显著的构型特点在于其“自运动”特性，也就是在末端位姿固定的情况下可以有无数组关节角度与之对应。如今已经有很多学者对七自由度机械臂的构型问题进行了大量的研究与分析，本文所使用的Diana V2 机械臂是思灵公司生产的一款轻量化协作机械臂，其构型为带有偏置的SRS 型，具备反应快、自适应、灵敏度高等优点，适合精密装配与在狭窄空间中作业。在建立机械臂坐标系的各种方法中，D-H 方法的应用是最为广泛的，本文采用改进后的D-H 方法描述机械臂的结构参数，并建立各个连杆的坐标系，该机械手臂的模型及DH 坐标系如图1 所示，机械臂D-H 参数值如表1 所示。

表1 冗余机械臂D-H 参数值Tab.1 D-H parameter value of manipulator

图1 机械臂模型及连杆坐标系Fig.1 Manipulator model and linkage coordinate system

2 机械臂运动学分析

2.1 正运动学

2.2 逆运动学

机械臂逆运动学与正运动学的求解过程相反，相对更为困难，是已知末端位姿求解机械臂各个关节的角度值。但是由于冗余机械臂自身的冗余特性，使得同一个末端位姿可以反解出无数组解，因此需要补充相应的约束条件求得唯一解。本文采用梯度投影法求运动学逆解，该方法求得的解由特解和齐次解2 部分组成，由于特解与齐次解是正交关系，因此梯度投影法在不影响完成首要任务的同时，能对次要任务进行优化。梯度投影法的公式为

式中：——逆运动学方程=的解，可以保证机械臂末端的运动规律；k(I-J+J)——=0的齐次解，是H∇ 在零空间的投影，该部分的作用是在不影响机械臂末端位姿的前提下，通过对目标函数的优化实现关节变量的最优化；k——梯度系数，其大小与优化速度呈正相关；H∇——优化目标H的梯度。

在实际应用场景中，梯度系数k的取值是难点，k取值过大易引发震荡，k取值较小则对机械臂关节运动的约束作用不明显，可能造成关节变量超出关节极限范围。

利用MATLAB 机器人工具箱对机械臂逆运动学算法进行验证，图2 为机械臂各关节角度分别为pi/2，-pi/4，-pi/2，pi/3，pi/2，3/4pi，-3/4pi 时 的仿真模型，将关节角度代入正运动学方程计算出对应的末端位姿矩阵，并将该位姿矩阵作为逆运动学算法的输入，计算得到各关节角度与初始值误差很小，且由图3 可知逆运动学解算出的关节角连续且平滑，而且角度变化范围也在各关节的运动范围之内，因此验证了逆运动学算法的正确性。

图2 机械臂仿真模型Fig.2 Simulation model of manipulator

图3 各关节角度变化曲线Fig.3 Joint angle change curve

2.3 工作空间求解

蒙特卡洛法是基于概率统计论对随机性问题进行仿真，机械臂末端的理论工作位置并不属于随机性问题，因此先将机械臂工作空间的解设计为统计参量，再利用该方法可在MATLAB 中求解得到该七自由度机械臂的工作空间。此次定义随机采样点数为5 000。随机采样点数越大，呈现出的工作空间范围则越接近真实的工作空间，可得到该机械臂的工作空间范围接近一个椭球体，机械臂工作空间云图如图4 所示。

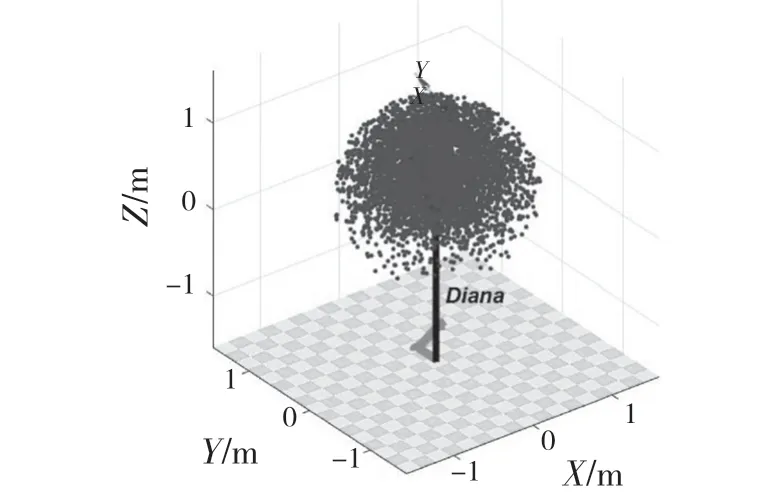
图4 机械臂工作空间云图Fig.4 Cloud map of manipulator workspace

3 机械臂动力学分析

3.1 动力学建模

动力学主要研究的是物体运动与力之间的关系，该机械臂所有关节均为旋转关节，故对其进行运动和关节力矩分析时，需要考虑各个连杆的惯性张量I。将机械臂各个连杆的质心C作为原点建立坐标系，则相对此坐标系惯性张量I 为

其中对角线元素为刚体绕坐标轴的质量惯性矩，其余元素为惯性积。机械臂各连杆的质量、质心位置、转动惯量等参数如表2 所示。

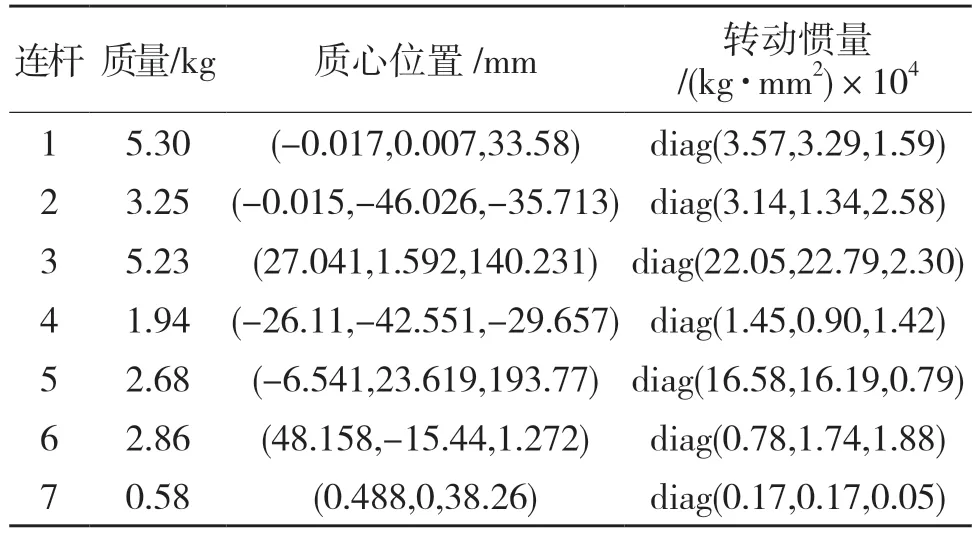
表2 机械臂属性参数Tab.2 Mechanical arm attribute parameters

研究机械臂动力学的方法有牛顿-欧拉法、拉格朗日法、旋量方法及凯恩方法等，鉴于Diana七自由度机械臂构型的复杂性，采用拉格朗日方法对其进行动力学分析。拉格朗日方法本质上是基于系统能量对时间采用微分的动力学方法，该方法基于能量平衡方程，更适合于分析同一系统中的多个连杆运动。

定义拉格朗日函数为L=K-P，其中：L——拉格朗日函数，K——机械臂系统总动能，P——系统总势能。对于Diana 七自由度机械臂而言，系统动能和势能分别为

连杆i的质心在连杆i局部坐标系中的位置为

机械臂各个关节力矩的推导方程为

式中：τi——机械臂广义力或力矩；θi——广义坐标；——广义坐标的1 阶导数。计算上述拉格朗日方程中的导数项可得新的各关节力矩表达式为

式（9）中的第1 部分代表机械臂广义加速度产生的惯性力对动力学的影响，第2 部分为科氏力和离心力项，第3 部分表示重力对关节转矩的影响。

本文以Diana 七自由度机械臂为实验平台进行动力学分析，将其动力学方程展开为

在七自由度冗余机械臂的运动过程中，科氏力与向心力对动力学的影响与转速呈正相关。通常大臂关节转速较慢，故可以忽略对动力学影响很小的科氏力与向心力，但同时小臂及腕部关节的转速相对较高，因此在求解动力学的过程中不可忽略。另外，角加速度与重力对机械臂运动的稳定性与精度有着较大的影响。故应当综合分析对机械臂动力学产生影响的因素并相应地做出简化，以得到各个关节的力矩推导公式。

3.2 动力学仿真

采用ADAMS 作为仿真平台对七自由度冗余机械臂进行动力学分析。首先基于SolidWorks 建立了冗余机械臂的三维模型，并将模型保存为Parasolid格式并导入ADAMS，需注意建立的模型应尽量简化，满足虚拟样机仿真性能的同时，构件数量尽可能少。在SolidWorks 中建立的简化模型如图5 所示。

图5 机械臂简化模型Fig.5 Simplified model of robotic arm

首先需要根据机械臂的实际需要设置仿真参数，从而预测机械臂的力矩值。将上述建立的机械臂模型导入到ADAMS 中，导入后对机械臂的属性进行定义，包括颜色、位置、名称和材料等，特别是质量信息，以确保仿真模型的质心与转动惯量与三维模型保持一致，然后再对机械臂添加约束，由于Diana 机械臂有7 个转动自由度，因此在机械臂各个关节处添加一个转动副，并在基座与大地之间添加一个固定副。设置完成后的模型如图6 所示。

图6 机械臂约束与驱动Fig.6 Constraint and drive of manipulator

为了使机械臂按照预定轨迹运动，需要对每个转动副设置相应的驱动，设置完成后的各关节初始关节角度均为0，目标关节角度依次为60，30，45，30，90，45，120。规划仿真时间为5 s，仿真步长设置为300。此时便可以求解系统中的反约束力，根据运动求作用力就是逆动力学问题。通过ADAMS 完成对机械臂的动态仿真后，从后处理模块中得到各关节仿真力矩随时间变化曲线。

另外，机械臂动力学求解包含大量的矩阵运算，因此需要在MATLAB 中对动力学理论模型进行相应的简化，将仿真得到的机械臂各关节运动物理量（角度、角速度、角加速度）作为动力学方程的输入，求出各个时间点对应的关节力矩值并拟合成相应的曲线，最后与上述仿真得到的力矩曲线进行对比。图7 为机械臂各关节理论力矩曲线和仿真力矩曲线的对比。

图7 各关节理论力矩曲线与仿真力矩曲线对比图Fig.7 Comparison diagram of theoretical torque curve and simulation torque curve of each joint

由图7 可知，相较其他关节，关节7 的驱动力矩最小，这是因为关节7 运动过程中仅有很小的负载，且负载集中在其关节轴线附近，因此即使有较大的角加速度，对驱动力矩的影响也很小；关节2的驱动力矩逐渐增大且幅值远大于其他关节，这是因为机械臂按照预定路径运动时，关节2 处所受的负载逐渐变大，且需要承受上部关节的重力和运动时产生的向心力及科氏力。通过观察各关节的力矩变化，总体可以看出各关节力矩受其余关节的耦合影响。通过机械臂各关节的力矩仿真曲线，分析各关节的动力学特性，为进一步研究机械臂控制及设备性能可靠性提供参考。

综上，七自由度机械臂按照规划路径运行时的理论与仿真力矩数据基本吻合，验证了动力学建模的准确性，因此上述建立的动力学方程可应用于后续的算法研究中，也为机械臂后续控制提供了试验基础。

4 结论

（1）采用改进D-H 法建立了冗余机械臂的连杆坐标系，推导出相应的运动学方程，基于梯度投影法求解其逆运动学问题，并利用MATLAB 机器人工具箱验证了算法的可靠性；（2）以拉格朗日方法为理论基础，建立了冗余机械臂的动力学模型，当机械臂运动时，可通过动力学方程计算出机械臂各个关节的理论力矩；（3）在SolidWorks 中建立了冗余机械臂的三维模型，将模型导入ADAMS 进行动力学仿真并绘制出仿真力矩曲线，将ADAMS仿真得到的运动信息作为MATLAB 动力学方程的输入，绘制理论力矩曲线。将两者进行对比，判断拟合程度，结果证明了动力学建模的可靠性。

本文对冗余机械臂运动学与动力学的分析研究为后续控制研究和运动优化提供了试验依据和理论基础。