大跨度悬挑桁架结构体系及稳定性研究

罗志锋， 康金明， 姚荣康， 张钧儒

（1. 华南理工大学建筑设计研究院有限公司；2. 华南理工大学土木与交通学院）

1 引言

桁架结构屋架形式一般有三种：平行弦式，梯形式，三角形式[1]。桁架结构用料经济、结构自重小、节点形式简单、刚度大、几何特性好，是最为适合用作悬挑的结构体系[2]。对于竖向不连续结构，桁架转换梁对于梁式转换在破坏形态、延性变形能力上有着显著的优势[3]。计算方法的假定、荷载作用位置、计算长度、构件截面形式、跨宽比及系杆的布置等都会对空间桁架结构体系的稳定性能产生极大的影响，也是此类结构研究设计之中的一个重点[4]。本文以某体育场看台悬挑桁架雨棚设计为例，对悬挑桁架整体稳定性进行有限元分析[5-6]。

2 工程概况

2.1 结构选型

某体育场看台雨棚共设置11榀悬挑桁架，每榀悬挑桁架由端部的四根呈W设置的斜柱支撑，悬挑跨度约为21.5m，悬挑段根部桁架高度约为2.4m，桁架高度随距离悬挑段端部距离的增大而逐渐变小，最末端桁架高度约为0.8m。桁架上下弦构件整体为上凸曲线。

2.2 材料

所有钢材材质均为Q355B。

3 悬挑桁架结构分析

3.1 悬挑桁架的基本组成

雨棚采用桁架结构，桁架上弦之间均匀设置系杆，并在雨棚四周设置连续的交叉支撑，形成整体性较强的空间网格结构。雨棚三维模型如图1所示。

屋盖结构由双向桁架结构、平面支撑及桁架之间的系杆等组成：纵向悬挑桁架，横向垂直支撑桁架，上弦平面支撑（包含与钢构件通过栓钉连接的混凝土面板），下弦平面支撑，如图2 所示。上弦平面与下弦平面在屋盖纵向两端汇交。由此，屋盖形成整体性较强的空间网格结构。

图2 屋盖整体三维模型拆解示意图

屋盖体系下方为钢管斜柱以及柱间支撑（见图3），斜柱及柱间支撑不仅能承担竖向压力和拉力，还有纵向与横向抗侧刚度，因此，结构也有较好的抗扭刚度。

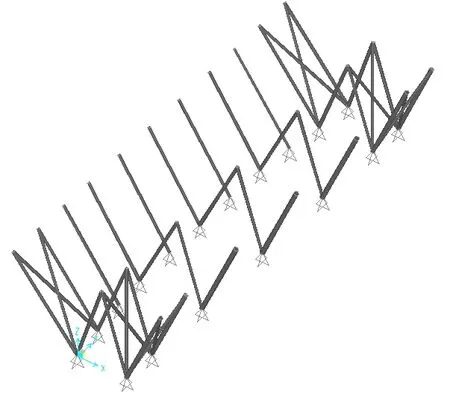
图3 钢管斜柱以及柱间支撑

3.2 纵向悬挑桁架平面内几何构成分析

下图为钢屋盖的两种平面桁架及对应力学模型示意图。从图4 的第一种桁架的力学简图来看，上部是由上弦构件、下弦构件以及腹杆组成的刚片（阴影区域），下部钢柱可简化为两根链杆A、C及一个固定铰支座B，从平面角度看，结构是几何不变体系。

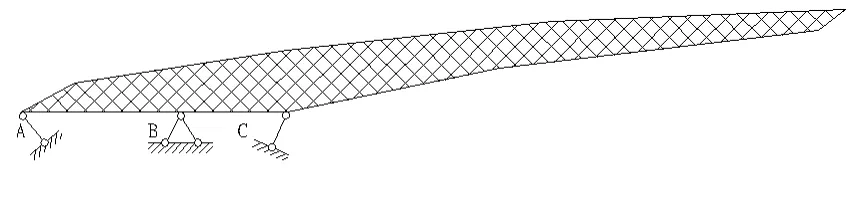
图4 钢屋盖第一种桁架形式示意图以及对应力学简图

图5为第二种桁架形式，其存在两个充当其托架梁的桁架（见图6），同第一种桁架，下部钢柱可简化为链杆A，两道托架桁架所起作用可以简化为平行的两根链杆B、C，同时上弦钢筋混凝土板的作用可以简化为平行上弦平面的链杆D。A与B、C与D不平行，从平面角度分析，结构也是几何不变体系。

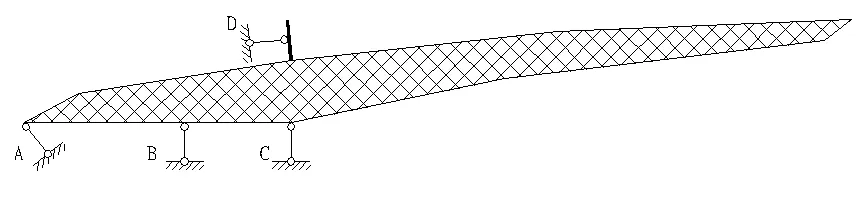
图5 钢屋盖第二种桁架形式示意图以及对应力学简图

综上，两种桁架形式从平面上分析是合理稳定的结构。

3.3 上、下弦平面几何构成分析

屋盖系统的上弦平面的D轴以上设有平面支撑，D轴以下设有现浇钢筋混凝土楼板，楼板厚度100mm，楼板与上弦构件通过栓钉固定连接（雨棚上弦结构平面图如图7所示），可保证本结构上弦平面的稳定。下弦平面上设置有两道与下部柱间支撑对应的水平支撑（雨棚下弦结构平面图如图8 所示），整体上，屋盖上下弦平面在两端连接在一起，下弦平面在纵向通过各榀悬挑架与上弦平面连接，横向通过托架桁架与上弦平面连接，同时两侧增设的水平支撑使其整个平面是稳定的，托架桁架不会受到水平外力的影响。

图7 雨棚上弦结构平面图

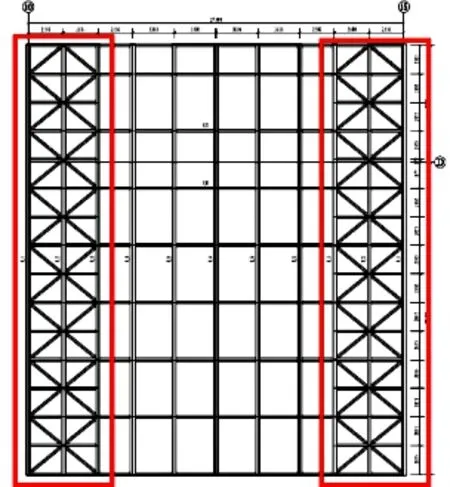
图8 雨棚下弦结构平面图

3.4 桁架整体稳定性分析

在桁架面外方面，下部柱列设置的柱间支撑可保证下部柱列的侧向稳定。为验证柱间支撑设置的必要性及合理性，文章对模型进行四种柱间支撑设置情况的整体侧向稳定性进行分析（D+L 工况），分别为：不设置柱间支撑、仅设置一道柱间支撑、设置两道柱间支撑以及设置三道柱间支撑。不设置柱间支撑时整体失稳对应屈曲因子为3.4，设置一道柱间支撑以及两道柱间支撑的分析结果如图9-图10 所示。根据分析结果可知，柱间支撑对整体侧向稳定非常重要，设置一道柱间支撑可大大提高整体侧向屈曲因子（从3.4 提高到22.3～31.1），最终模型设置三道柱间支撑，可以充分保证屋盖结构整体侧向稳定性（相应屈曲因子可达到48.87）。

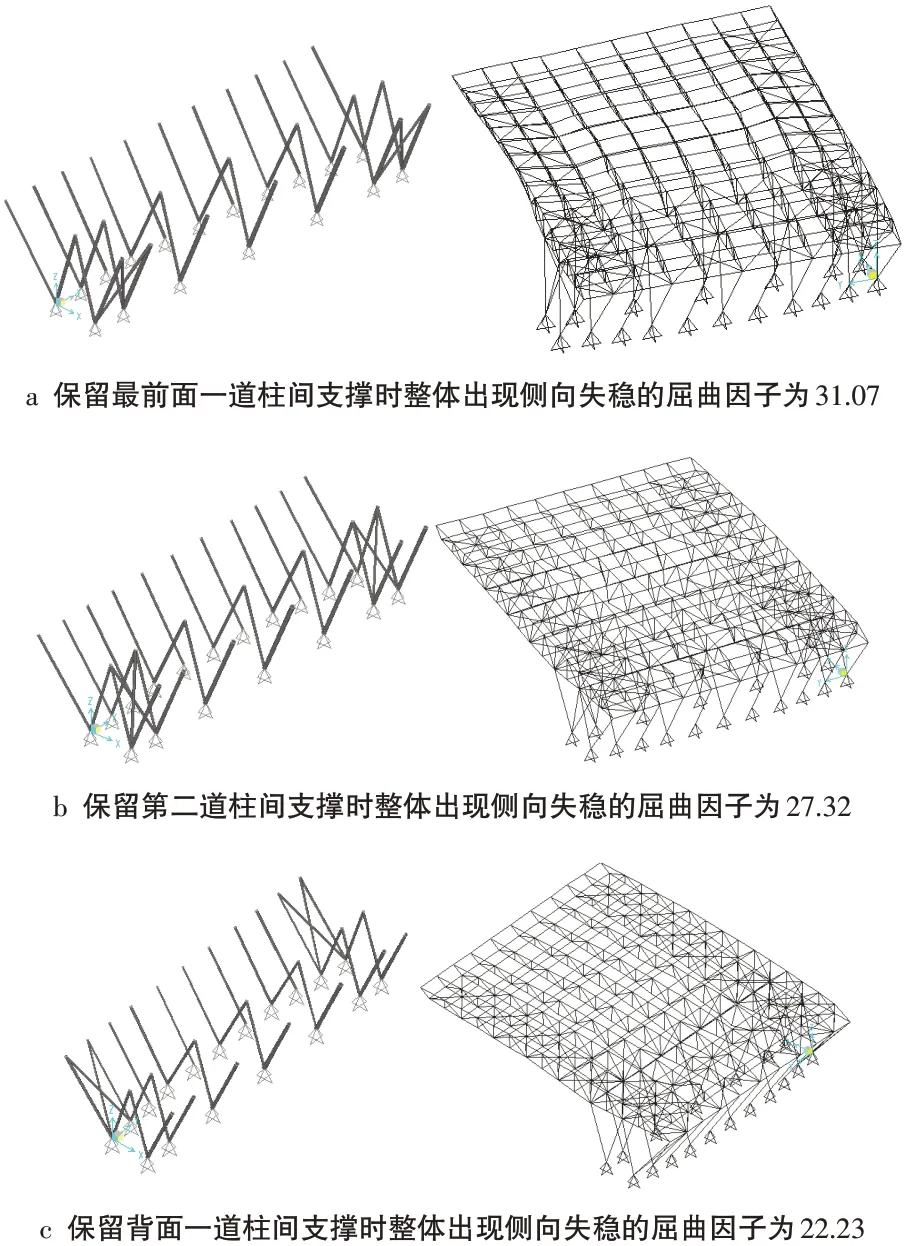
图9 当屋盖仅设置一道柱间支撑时整体稳定性

3.5 托架桁架面外受力

托架桁架的上弦构件兼作悬挑屋盖的上弦横向连系杆、下弦构件为悬挑屋盖的下弦连系杆、直腹杆同时也是悬挑桁架的直腹杆。悬挑屋盖的上、下弦平面具有很强的整体面内刚度，所以，托架桁架不会产生较大的平面外位移差。

计算时考虑了将屋盖模型中托架桁架在两榀桁架之间的杆件设置为两端刚接和两端铰接（释放两个主轴方向的弯矩约束）的情况。当托架杆件两端铰接，且屋盖上弦混凝土板的面内刚度折减一半时，托架桁架上下弦节点在竖向的位移值可控。由于悬挑桁架在竖向荷载作用下整体前倾下挠，托架存在面外的整体扭转。但此位移并不大，可为托架承担。

另外根据D+L 下悬挑架最外端竖向位移值（148mm）以及托架梁位置竖向位移值(9.6mm)可得出整体转角，根据托架梁位置到悬挑架最外端的水平距离（21.6m）以及托架梁高度（2.4m）反算得托架梁上下弦面外相对位移值理论计算约为15mm，实际分析结果相对位移值约为10mm，在可控范围之内。

3.6 悬挑架下弦杆件面外稳定

从整体屈曲计算结果可知，在D+W-的情况下，悬挑部分下弦构件稳定因子为13.37，根据下弦杆件在单倍D+W-的轴力、截面绕弱轴惯性矩以及腹杆间距范围内下弦构件的几何长度，通过欧拉公式进行反推：

式（1）中：E为弹性模量，N/M2；I为惯性矩,M4；μ为计算长度系数；l为构件几何长度；P为轴向荷载大小，Pa。

得到下弦构件面外计算长度系数为1.61。从下弦构件D+W-下的第一阶正值屈曲模态（见图11）可以看出，下弦构件反弯点间的距离约为2 倍构件长度，所以，设计时下弦构件的计算长度系数取为2，杆件仍然处于正常使用状态。

4 结语

通过对某体育场看台悬挑雨棚几何构成分析及稳定性分析，再由局部失稳到整体稳定理论分析，得出结论如下：

①大跨度悬挑空间桁架结构的设计在保证平面内、外稳定性外，应尽可能灵活布置，使力的传递更加合理，使得建筑更具艺术性；

②上弦平面增设的混凝土楼板不仅增加了上弦平面的面内刚度，还增加了雨棚的抵御风荷载作用的能力，同时加强支撑的整体性，既增强了传递侧向力的可靠性，调整上、下弦平面支撑设置位置，使上、下弦平面支撑与下部柱间支撑对齐，尽量向混凝土板一侧多设置一跨平面支撑；

③对于悬挑桁架结构，斜柱的设计能够很好承受不规则扭转的作用，同时亦可增加柱间支撑来增加悬挑桁架结构的整体稳定性；

④托架梁、托架桁架面外受力发生位移是工程中普遍存在的情况，经分析，其位移值在可控范围之内，不会对结构正常使用产生影响。