大跨度钢管混凝土系杆拱桥吊杆索力分析

王宪玉,王兴武,梁 孝,周 敏,杜永峰

(1.兰州理工大学 防震减灾研究所,兰州 730030;2.甘肃省交通规划勘察设计院股份有限公司,兰州 730030;3.西南交通大学 土木工程学院,成都 610031;4.内江师范学院,四川 内江 641000)

钢管混凝土系杆拱桥是梁-拱组合受力结构,其充分发挥拱肋受压及系梁受弯的力学特性,使得桥梁结构受力更为合理且节省施工成本[1]。其中,吊杆在梁-拱组合结构中起到连接和传力的关键作用,吊杆结构受力是否均匀直接关系到桥梁结构受力是否合理,因此准确的对吊杆索力进行分析是十分重要的。

它不仅是评估钢管混凝土系杆拱桥在设计、成桥阶段受力合理性的要素之一,也是评定运营阶段结构健康状况的重要指标。一般根据吊杆抗弯刚度的差异,将吊杆分为柔性吊杆、半刚半柔性吊杆及刚性吊杆[2]。

目前,桥梁设计阶段吊杆索力优化常用方法包括内力平衡法、零位移法、刚性支承连续梁法、弯曲能量最小法等[3-4]。桥梁成桥及运营阶段吊杆索力测量方法有压力传感器法、波动法、磁通量法、千斤顶油压法及振动频率法等,其中频率法最为实用。为准确测量和计算吊杆索力,国内外学者纷纷进行研究[5-9],其中包括吊杆边界条件、计算长度、环境温度及自身参数等因素。现阶段研究中,暂未完整的从桥梁的设计优化、成桥测试及运营测试对索力进行分析;暂未考虑索力测量位置对索力数值的影响,且未全面考虑阻尼器及自身参数的综合影响,致使测量索力仍存在一定误差。为了更好地的解决以上问题,本文结合实际工程实例应用能量法推导相应索力计算公式,并从索力的优化、索力的实测位置及日后运营维护的索力测试手段为切入点,提出相应优化及测试建议。一并提出在成桥阶段应准确测算吊杆抗弯刚度的测量方法,可有效减小在运营阶段索力测试不准的问题。

1 柔性吊杆索力模型分析

取任意倾斜柔性吊杆拉索放置在以拉索为X轴和垂直于拉索为Y轴的直角坐标系下。吊杆基本特性参数如图1所示。

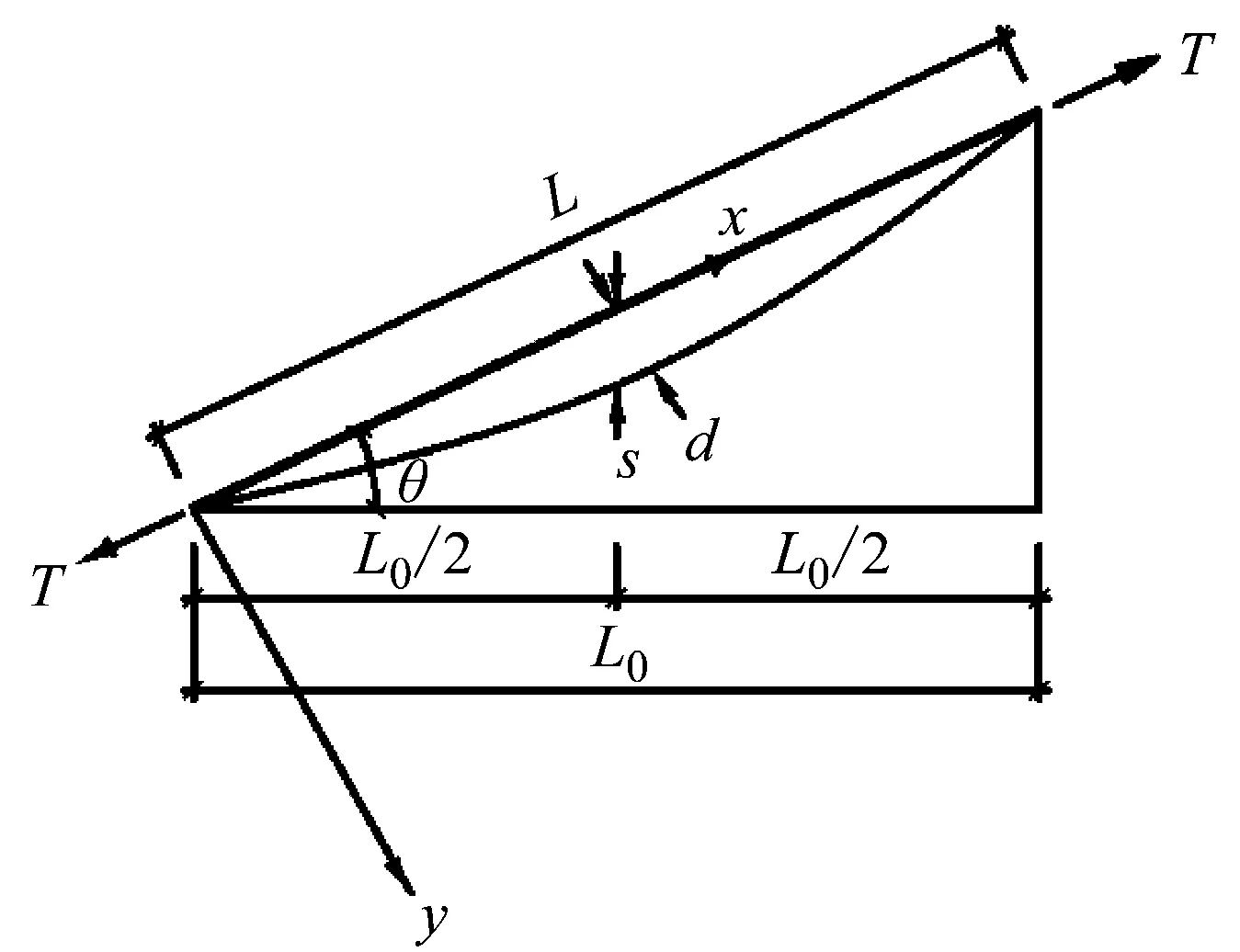
图1 吊杆基本特性参数Fig.1 Basic characteristic parameters of boom

根据能量守恒定律为基础的瑞利法[10]可以表示为

E+V=C=Emax=Vmax

(1)

进而需假设系统结构的一般振型函数[11]

y(x,t)=φ(x)cos(ωt+θ)

(2)

式中:ω为拉索振动的圆频率;θ为吊杆倾斜角。

系统结构的总动能E和总位能V表示为

(3)

(4)

式中:m为拉索的线密度;T为吊杆索力。

进而求得系统结构的最大动能Emax为

(5)

式(3)～(5)代入式(1)得

ω2=

(6)

当两端边界条件不同时,结构的振型函数也有不同,对于两端铰接、一端铰接一端固结、两端固结时的索力公式分析如下:

(1) 边界条件为两端铰接

因其阵型函数和简支结构相似,表示为

(7)

对式(7)的x求1阶和2阶导数并代入式(6),进而求得索力公式

(8)

(2) 边界条件为一端铰接一端固结

因结构的高阶振型很难求得,故设一阶阵型为[12]

(9)

将式(9)代入式(6),进而求得索力公式

(10)

(3) 两端固结

因结构的高阶振型很难求得,故设一阶阵型为

(11)

将式(11)代入式(6),进而求得索力公式

(12)

2 柔性吊杆索力优化分析

2.1 研究背景

本文以某钢管混凝土系杆拱桥为研究背景,该桥由主桥和引桥组成,总长1 254.4 m。主桥为132 m下承式钢管混凝土系杆拱桥,引桥为预应力连续梁结构。主桥拱圈计算跨度132 m,矢高26.4 m,矢跨比1/5,拱轴线采用悬链线,拱轴系数m=1.347。系杆拱整体结构体系为拱脚、桥墩墩顶和端横梁三者固结为一体,使拱圈与桥墩组成为刚架结构;主梁为纵横梁体系的结构,悬吊于拱圈下方,它两端与拱肋不连接,为漂浮体系。主拱圈水平推力由系梁中的系杆承担。

主桥采用MIDAS CIVIL进行建模模拟(共计538个节点、718个单元、46个节点弹性连接、8个弹性连接、52个刚性连接及177个一般支撑模拟。其中,主拱、纵梁、横梁、墩柱采用梁单元,吊杆、系杆采用桁架单元。)

该桥整体结构体系为拱脚、桥墩墩顶和端横梁三者固结为一体,拱圈与桥墩组成为刚架结构,故模型中建立桥墩,以模拟其纵向抗推刚度。主梁为纵横梁体系结构,悬吊于拱圈下方,两端与拱肋不连接,为漂浮体系,模型中考虑漂浮体系的影响。另外,横梁在中吊杆处为牛腿构造,设置了板式橡胶支座,此处采用释放梁端RX、RY、RZ自由度约束进行模拟。主桥模型如图2所示。

图2 主桥MIDAS模型图Fig.2 Main bridge MIDAS model diagram

主桥拱圈由一片中拱肋和两片边拱肋组成(本文选取中拱肋吊杆为研究对象),拱圈采用等截面哑铃形式,拱肋空腔内均填筑C50微膨胀混凝土。每片拱肋设吊杆21组,三片拱肋一共63组,每组吊杆都由2根钢束组成,其中边吊杆为2束12-7Φ5无黏结钢绞线,中拱肋吊杆为2束19-7Φ5无黏结钢绞线,吊杆在下端设2.5 m钢套管,拱肋内设防漏钢管,其余外套均为PVC管。本文吊杆长度均为叉耳与连接器之间的长度,文章不在赘述。主桥立面图及吊杆编号如图3所示。

图3 钢管拱混凝土系杆拱桥立面图及吊杆编号图Fig.3 Elevation drawing and derrick number drawing of arch concrete-filled steel tube tied arch bridge

2.2 吊杆索力优化分析

吊杆索力优化就是能找到一组吊杆索力,使结构体系在确定性荷载作用下,某种反映结构受力性能指标达到最优[13]。

本文主桥在服役期间需要更换吊杆,更换后的吊杆位置、吊杆根数均与原设计保持一致。应用有限元模型计算得出吊杆的初算索力,提取中拱肋吊杆在恒载状态下的索力值如表1所示。

表1 中拱肋吊杆参数及索力计算值Tab.1 Parameters of the arch rib boom and cable force calculation value

分析表1发现N2、N2′吊杆索力较大,受力过于集中,需进行索力优化。本文应用MIDAS CIVIL未知荷载系数功能,对吊杆索力进行优化,使得吊杆的受力均匀、系梁位移、拱肋弯矩合理。优化后的桥梁在恒载作用下系梁变形最大5.04 cm,拱脚截面弯矩-2 573.45 kN·m、拱顶截面弯矩2 944.22 kN·m。中拱肋优化后索力值如表2所示。索力优化前后对比图如图4所示。位移、弯矩如图5、图6所示。

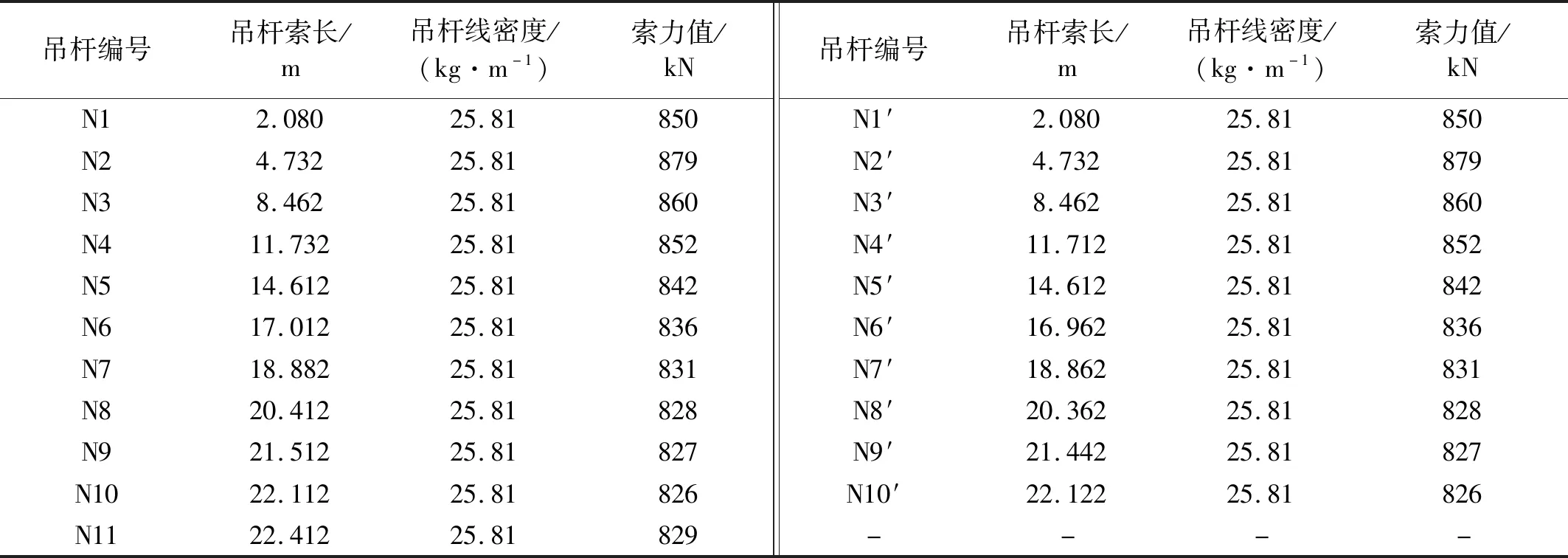
表2 中拱肋吊杆参数及优化后索力值Tab.2 Arch rib boom parameters and optimized cable force value

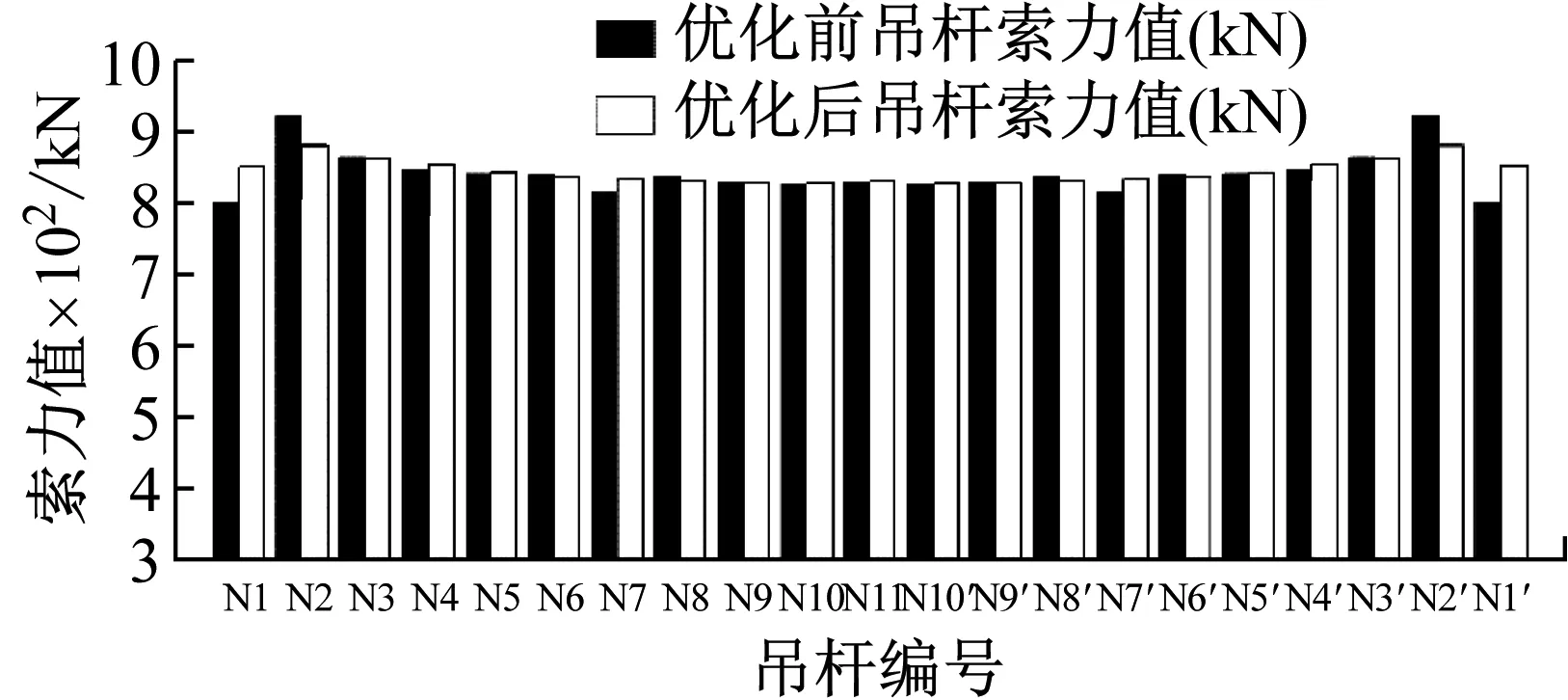
图4 吊杆索力优化前后对比图Fig.4 Comparison diagram before and after optimization of boom cable force

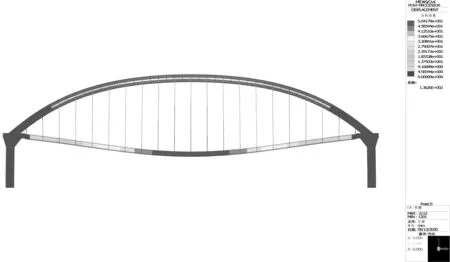
图5 吊杆索力优化后梁体位移图Fig.5 Position shift diagram of the rear beam after the suspension cable force optimization

图6 吊杆索力优化后拱肋弯矩图Fig.6 Bending moment diagram of arch rib after suspension cable force optimization

3 柔性吊杆索力(频率法)测试分析

待吊杆全部更换完成后,拆除现场桥面脚手架、模板及现场施工设备,采用DH5906W无线索力测试仪和DHDAS动态信号采集分析系统对中拱肋吊杆索力进行采集与分析。将无线索力测试仪依次绑在N7吊杆的不同位置(12等分点),分别测试在同根吊杆不同位置采集的振动频率。吊杆上、下锚头锚固形式如图7所示。测试位置如图8所示。测试结果如图9所示。现场测试照片如图10所示。

图7 上、下锚头锚固形式Fig.7 Anchorage form of upper and lower anchor heads

图8 N7吊杆索力测试位置Fig.8 Test position of N7.boom cable force

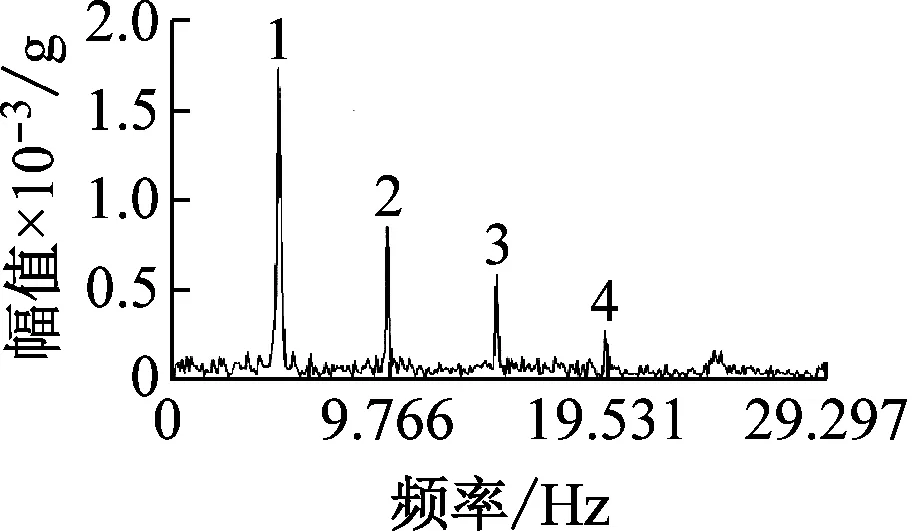
(a) 测点在L/12处

图10 吊杆索力现场实测照片Fig.10 Field measurement of boom cable force

通过对吊杆在不同位置的实测振动频谱分析得出:

(1) 不同位置传感器测得的N7吊杆振动基频为4.773～4.783 Hz(现场环境实测略有干扰),各测点传感器振动频率基本一致,但振动波形略有不同。

(2) 在靠近吊杆端头处的低阶频率识别较好,但波形处理后线型不平顺。低频信号存在干扰,现场吊杆索力实测时测点应尽可能远离吊杆端部。

(3) 对比图9(e)和(g)测点频率谱可知:对称测点的振动频率和振动波形基本一致,表明所测吊杆材质均匀且吊杆两端约束相同。因处于对称位置的吊杆振动频谱相似,故其余吊杆振动频谱未全部列出。

(4) 由图9(d)测点频率谱可以看出L/3处测点的3阶振动频率很难识别,且3阶波形附近不平顺。原因是柔性吊杆在振动的过程中3阶振型模态的节点处于吊杆的L/3及2L/3处。现场吊杆索力实测时测点应尽可能避免放在振型的模态点上。

(5) 由图9(c)、(f)测点频率谱可以看出L/4处测点4阶振动频率及L/2处测点2和4阶振动频率不明显。原因在于柔性吊杆在测试中出现“漏频”[14]现象。吊杆的L/2处是偶数阶振型的模态点,当吊杆处于偶数阶次振动时,L/2处的响应趋近于无限小(零),这种现象致使振动频谱偶数阶振动频率的峰值不明显。

(6) 根据以上第4、5点可以间接得出柔性吊杆的振动模态与简支结构振动模态相似。

(7) 测点在L/12、L/6、5L/12处(对称测点不全部列举)均能测出吊杆振动的前4频率,且振动波形图较为平顺。其中L/6及5L/12处测点振动加速度较为明显。故可以作为现场实测索力的首选点位,但考虑柔性吊杆一般较长现场测试不便,故建议现场吊杆索力实测时宜选择吊杆的L/6～L/4处进行测试。

4 柔性吊杆索力抗弯刚度识别及影响分析

桥梁在运营阶段吊杆抗弯刚度是很难准确识别的,一般通过公式近似计算,但近似计算有时误差较大,学者们为准确识别抗弯刚度纷纷进行研究[15-16]。其中学者吴海军在文献中表明,当索体长度<40 m时,不考虑抗弯刚度的影响,则会导致索力产生较大误差。因此对吊杆索力抗弯刚度准确识别是有非常必要的。

通过上节分析,现场将索力测试仪放在吊杆的L/6～L/4处进行实测。并通过下锚头预设压力环现场采集每一组吊杆实际索力值。因吊杆N1、N2、N1′、N2′索体长度均较短且索力测试仪实测吊杆频率不稳定,故本文选取吊杆N3～N11及N3’～N10’为索力研究对象,中拱肋吊杆索力及基频实测值如表3所示。

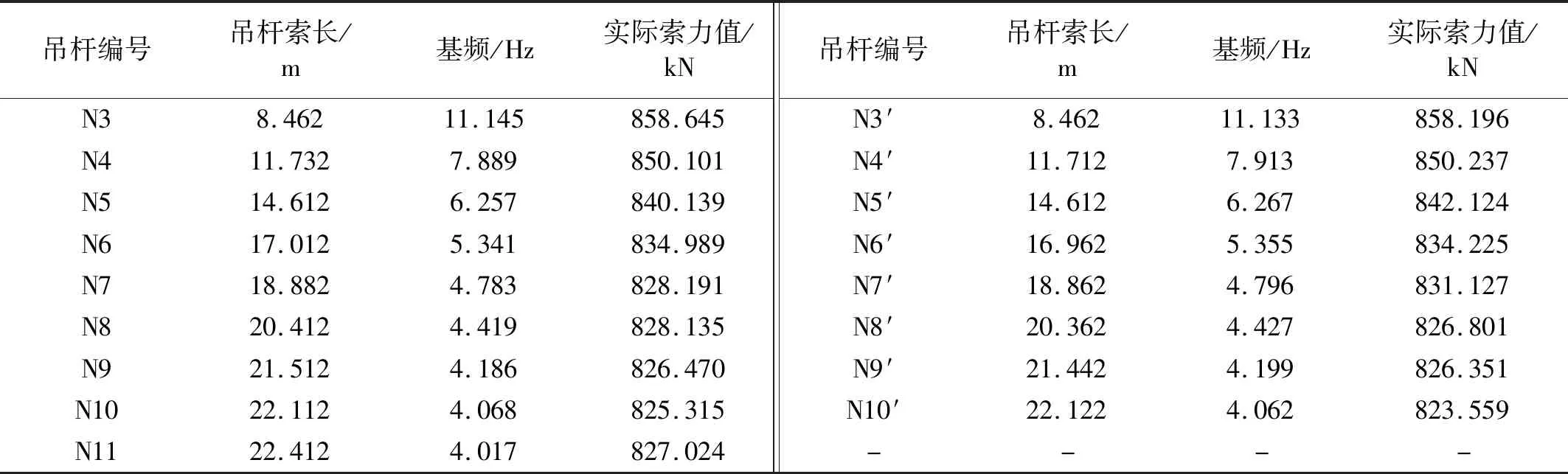
表3 中拱肋吊杆实际索力及振动频率Tab.3 Actual cable force and vibration frequency of the arch rib boom

将表3实测数据代入第1章推导的柔性吊杆索力式(8)、(10)、(12)进行反算识别,分析主桥吊杆索力两端约束形式。因吊杆处于竖直状态,故不再考虑吊杆倾角修正项。吊杆抗弯刚度计算结果如表4所示。

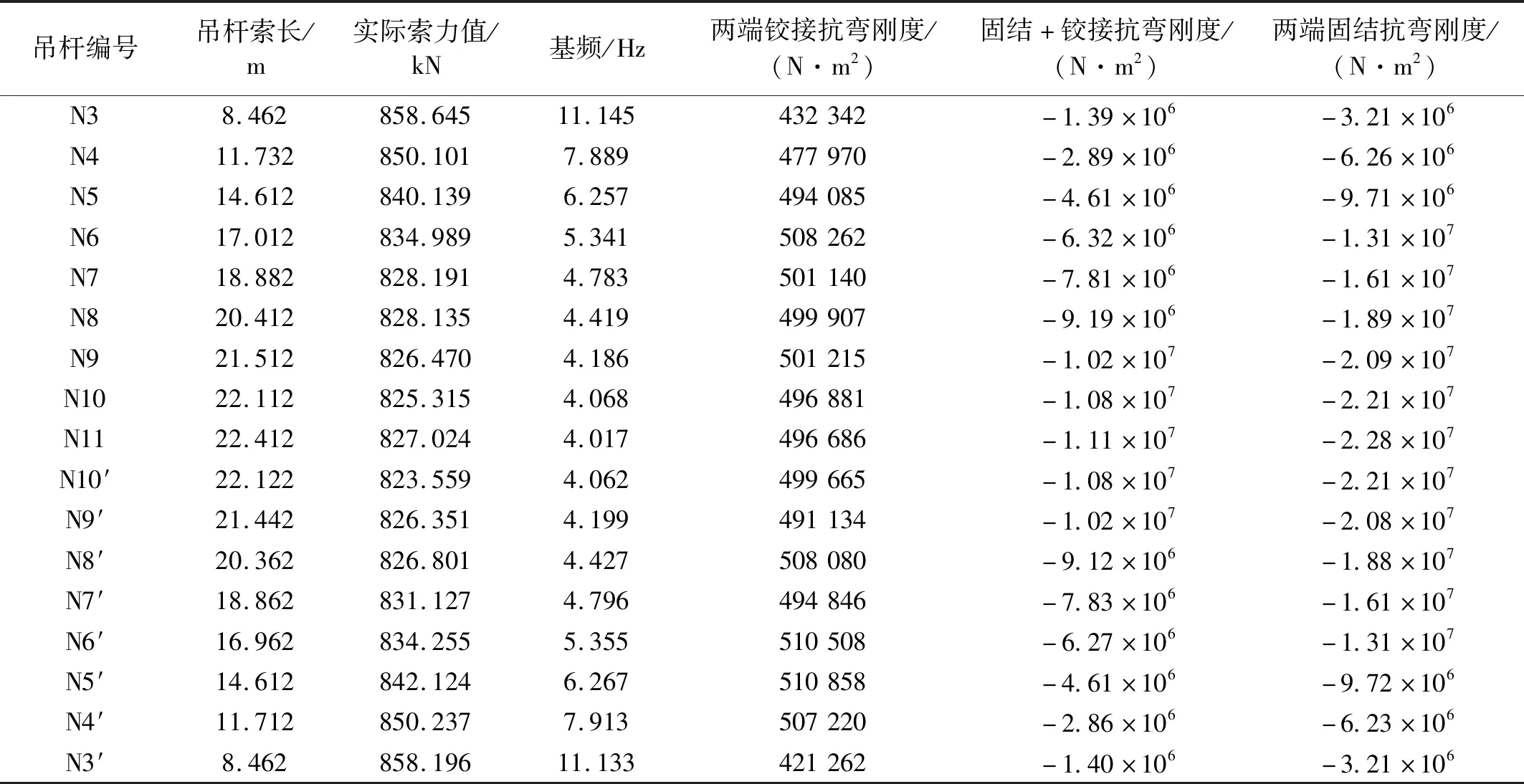
表4 中拱肋吊杆抗弯刚度识别Tab.4 Identification of bending stiffness of arch rib derrick

通过对表4的计算结果分析:本桥中拱肋吊杆上、下锚头虽为刚性锚头,但由于索体很长且两端设有叉耳及连接器,下锚头在叉耳端部表现出等效铰接。上锚头拉杆比柔性吊杆短且抗弯刚度大,在吊杆连接器端部表现出等效铰接,两铰接之间为吊杆的等效计算长度[18]。因本节重点在于提出抗弯刚度修正方法,且本文吊杆长度均为叉耳与连接器之间的长度。故取计算出的抗弯刚度平均值EI=491 298 N·m2作为中拱肋吊杆抗弯刚度识别代表值。

为准确判定抗弯刚度对索力值得影响,查阅相关规范[19]得知:钢丝束断面成正六边形或缺角六边形紧密排列。通过公式计算求得中拱肋吊杆高强钢丝束抗弯刚度EI=322 719 N·m2。可见与实际抗弯刚度还是有一定误差。

为减少抗弯刚度的影响,学者提出可用多阶频率计算索力。本文应用式(8)分别求解一阶及二阶索力公式。

(13)

(14)

同根吊杆索力相同,进而推导出索力变形公式

(15)

为定量知道抗弯刚度对索力值的影响,分别求出考虑计算抗弯刚度、不考虑抗弯刚度索力值以及应用多阶频率(选取一阶、二阶)计算的索力值,将他们与实际索力值进行对比分析。计算结果见表5、图11。其中T0为实际索力值、T1为考虑计算抗弯刚度的索力值、T2为不考虑抗弯刚度的索力值、T3为应用一阶、二阶频率计算的索力值。

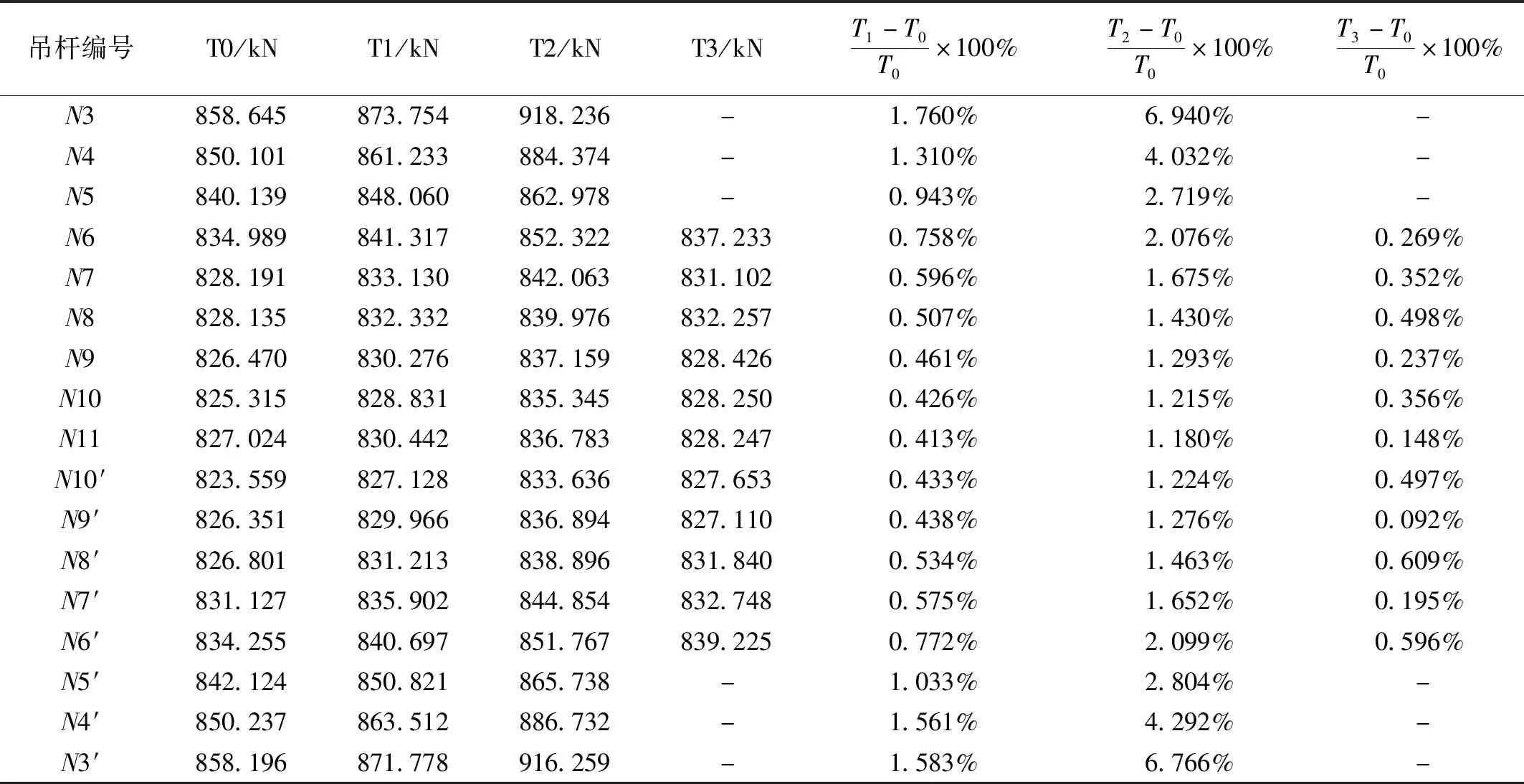
表5 吊杆抗弯刚度的影响Tab.5 Influence of bending stiffness of boom

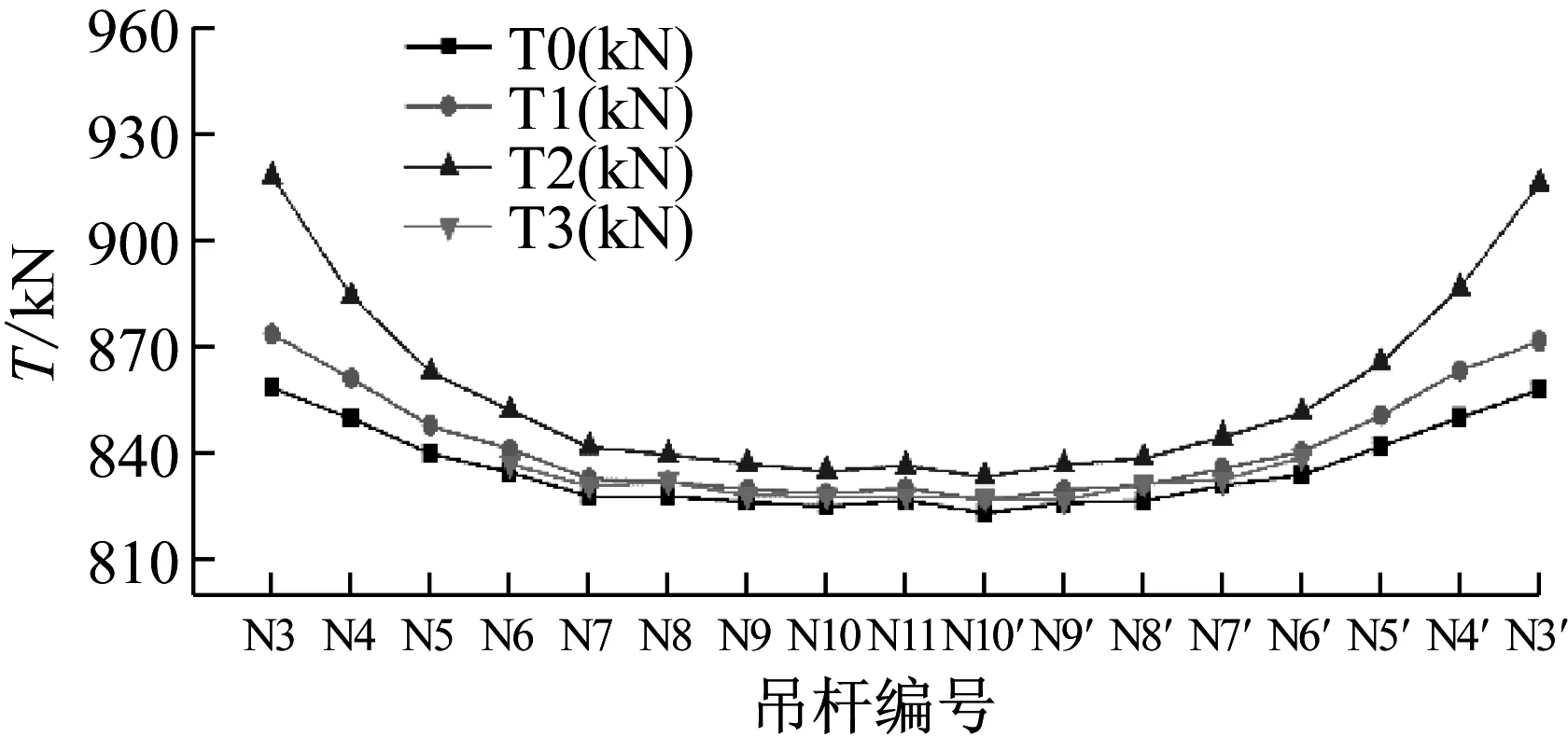
图11 索力值对比图Fig.11 Comparison of cable force values

通过对柔性吊杆索力抗弯刚度识别分析得知:

(1) 吊杆的实测抗弯刚度EI=491 298 N·m2比吊杆高强钢丝束计算抗弯刚度EI=322 719 N·m2大,原因在于计算时假定吊杆截面为圆形并仅考虑了高强钢丝束圆形截面的惯性矩。而实际中的吊杆除钢绞线外、还有防腐材质、HDPE保护套等材质、且在吊杆两端设置有阻尼装置,因此通过计算求得的抗弯刚度比实际抗弯刚度低。

(2) 由表5和图11得知:吊杆的抗弯刚度对索力值存在影响(尤其是短吊杆对抗弯刚度更为敏感),考虑计算抗弯刚度的索力值与实际值存在1.76%(最大值)的偏差率,不考虑抗弯刚度的计算索力值与实际值存在6.94%(最大值)的偏差率。因此,短吊杆索力计算应考虑抗弯刚度的影响。

(3) 应用多阶(一阶、二阶)频率计算的索力值与实际值存在0.609%(最大值)的偏差率,误差相对较小且稳定,但二阶及高阶频率现场采集有时难以测量,该方法存在一定现场测量难度。

(4) 桥梁在运营阶段经常应用频率法测试吊杆索力,故建议在成桥阶段应准确测算吊杆的抗弯刚度,为日后桥梁运营阶段索力的准确测试提供计算依据。

5 结 论

本文以大跨度钢管混凝土系杆拱桥吊杆索力为研究对象,基于能量法推导不同约束条件索力公式为基础,从设计阶段索力优化、成桥阶段索力实测及运营阶段索力刚度影响三个方面对大跨度系杆拱桥吊杆索力进行分析,得到以下结论:

(1) 应用能量法推导的索力公式是可行的。通过应用未知荷载系数法对索力进行优化,使得吊杆索力更为均匀、系梁位移更加合理。为施工阶段索力张拉及施工监控内力、位移数据监控提供基础,为同类桥型吊杆索力优化提供参考价值。

(2) 在环境激振作用下大跨度系杆拱桥柔性吊杆的振动模态与简支结构相似。建议在应用频率法测试吊杆索力时,测试点位宜放在吊杆L/6～L/4处,尽可能远离吊杆两端并避免放置在阵型的模态节点处,以减少端部低频信号对基频的影响及出现“漏频”现象。

(3) 大跨度系杆拱桥柔性吊杆的实际抗弯刚度与计算抗弯刚度存在差异,且吊杆索力值受抗弯刚度影响。其中考虑计算抗弯刚度索力值与实际值存在1.76%(最大值)的偏差率,不考虑抗弯刚度索力值与实际值存在6.940%(最大值)的偏差率,多阶(一阶、二阶)频率计算的索力值与实际值与实际值存在0.609%(最大值)的偏差率。因此为保证运营阶段吊杆索力的准确测量,提出成桥阶段应测量吊杆实际抗弯刚度的修正方法。