基于多域多尺度深度特征自适应融合的焊缝缺陷检测研究

张 睿,高美蓉,傅留虎,张鹏云,白晓露,赵 娜

(1.太原科技大学 计算机科学与技术学院,太原 030024;2.山西省机电设计研究院有限公司,太原 030009)

为满足现代制造技术高性能和功能多样化的发展需求,以奥氏体不锈钢为代表的现代制造业基础材料的应用日趋增多,在不锈钢工件焊接过程焊缝常会产生夹渣、未焊透、未熔合等缺陷。由于忽视焊接质量造成的事故屡见不鲜,因此必须加强不锈钢焊缝的质量检测,提高缺陷识别的准确率。在实际缺陷检测中,人工识别和机器识别的方法仍占据大多数,易受主观感受和经验主导且计算成本较高,目前已难以适用。随着深度学习在图像分类方面显现出的优势,人们开始尝试将深度学习技术应用于焊缝缺陷的自动化检测。

王睿等[1]提出基于轻量级倒残差结构的YOLO-M网络,采用多尺度预测机制分层预测不同缺陷特征,对X射线焊接图像中缺陷的预测精度达到93.5%。Ajmi等[2]使用改进的VGGNet网络和数据增强以及分别用Canny边缘映射和自适应高斯阈值提供的二值图像替代原焊接X射线RGB三通道图像中的通道B(蓝色)和通道G(绿色),实现了对未焊透,销孔,气孔三类焊缝缺陷较好的分类结果。黄焕东等[3]通过对焊缝缺陷的TOFD二维超声焊缝缺陷图像特征与缺陷轮廓关系的分析,提出一种基于区域卷积神经网络(Faster RCNN)的深度学习模型,在超声波衍射时差法构建的数据集基础上的实现了对裂纹、气孔、夹渣、未焊透和未熔合五类焊缝缺陷类型的自动识别。以上研究方法均在焊缝缺陷识别领域取得了一定成效,但在实际工程应用中,X射线检测方法存在安全性问题,实时检测很难实现。光学传感方法不能很好的获取到金属材料内部缺陷特征,TOFD二维成像方法又对设备超声探头横向、纵向分辨率性能以及实时性性能要求较高,较难在实际工程开展应用。

近年来,多使用超声回波法对焊缝缺陷进行检测,其检测装备价格相对便宜且更安全快捷。胡宏伟等[4]采用LBP-KPCA算法提取缺陷回波信号特征,利用基于径向基核函数的支持向量机对夹渣、气孔和未焊透三类焊缝缺陷类型的自动分类。Wang等[5]从时域和频域特征出发,在最终提取了9个特征值的情况下,对良好点焊接头、合格点焊接头和不合格点焊接头采用BP神经网络分类器和粒子群优化支持向量机方法达到了95%的识别率。Murta[6]等模拟了超声在二维介质中的传播,每个介质均包含模拟焊接接头缺陷的不同类型的模拟不连续点。采用聚类和分类(主成分分析和k-近邻)算法将每个A扫超声信号与其对应的建模缺陷关联起来,结果表明信号包络的主成分分析算法对气孔、裂纹和未焊透三类缺陷的正确分类率可达76.85%,k临近算法的成功率为73.14%。Silva等[7]提出了一种以深度极限学习机为基础的决策支持系统,将超声波衍射时差法信号分段的频谱作为训练特征,可较好地识别出焊缝未熔合、未焊透、夹渣和气孔四种缺陷类型。通过以上研究,基于超声回波信号的焊缝检测方法是具备可行性的,但仍然存在一些挑战:(1) 现有研究大多是基于时域或频域两种实数域分析所得信息开展焊缝缺陷类型检测,均忽视检测原始数据的复数域形式,仅依赖实部信息进行特征提取而忽视虚部数据的相位上的非线性信息及信号变化率,且对于一维超声信号的其余映射方式,以及映射后高维空间域中色相、明度、纯度等空间分量的互补与联立相关研究甚少。(2) 焊缝缺陷检测模型的建立不仅需要设计者具有丰富专业知识和领域知识,权衡模型大小和计算效率,还需在构建模型时反复试验以获得最佳模型参数,面对新的现实问题时往往需要重新构建模型,既耗时耗力又难以保证网络的鲁棒性和泛化性,进而制约了实际工程中焊缝缺陷检测方法的落地应用。

综上分析,本文结合实际工程应用需求,开展基于多域多尺度深度特征自适应融合的焊缝缺陷检测研究。对一维超声检测信号进行实数域、复数域等高维空间域映射,利用模型优化策略自适应寻优得到焊缝缺陷类型检测模型进行多域深度特征融合,最终通过复数全连接层实现对奥氏体不锈钢焊缝缺陷类型的识别与诊断。

本文整体框架如图1所示,主要分为三部分。第一部分是一维超声检测信号多域表征方法研究:将一维超声信号序列映射到复数域与多个候选实数域,对比效果选取特征信息表征能力强的两个实数域以及复数域作为本模型的特征域;第二部分是基于多域多尺度焊缝缺陷深度特征融合策略的焊缝缺陷类型检测模型构建(multi-domain and multi-scale fusion detection model of weld defect depth feature,MDMF):通过本文提出的深度半密集特征提取器(depth semi-dense feature extractor,PSD)充分分析检测信号的实数域和复数域特性,实现焊缝缺陷特征的完备性提取并基于多域特征融合策略将选定的特征域信息融合以实现更精确的焊缝缺陷类型识别;第三部分提出了面向卷积神经网络多维超参数自寻优的模型优化策略:基于分组通信改良的莱维混沌平衡优化器优化算法(improved Levy chaos equilibrium optimizer algorithm based on packet communication,PEO)对MDMF卷积网络模型的9个关键参数自寻优得到优化后的模型(adaptive multi-domain and multi-scale fusion detection model of weld defect depth feature,AMDMF),为不锈钢焊缝缺陷识别自适应地寻找一个效果较优的模型,并用于奥氏体不锈钢焊缝五类缺陷的识别。

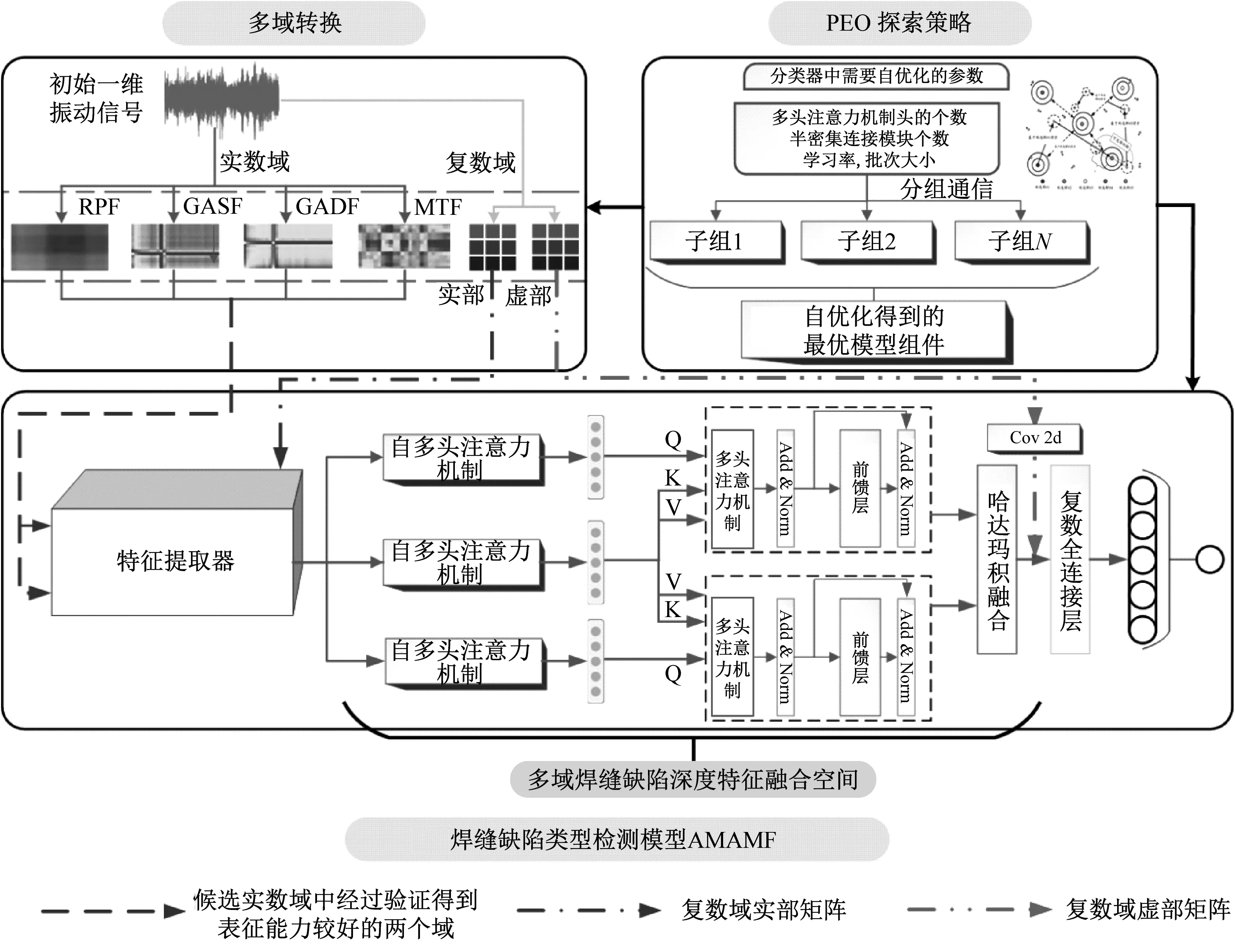
图1 模型总体架构Fig.1 Overall architecture of the model

本文的主要贡献如下:

(1) 提出面向焊缝超声检测的多域多尺度特征信息融合模型。从序列周期性、相关性、时空转换等角度出发,将一维超声信号衍生至复数域和实数域的格拉姆角场域、马尔科夫转移场域、递归域等高维空间域中,引入深度半密集特征提取器PSD提取出多域样本在时间和空间两个维度上的特征信息,基于多域焊缝缺陷深度特征融合的思想,利用不同域的特点通过多头注意力机制将复数域和实数域提取的不同特征信息相融合,得到更丰富的焊缝缺陷特征。提高焊缝缺陷类型的检测精度和数值稳定性的同时为多场景域下的信息融合提供思路。

(2) 提出面向卷积神经网络多维超参数自寻优的PEO模型优化策略。为进一步提升原始平衡优化器算法全局寻优效能以及开拓能力,依次引入莱维初始化、混沌浓度更新以及分组通信策略对其进行改良,并将改良后的PEO应用于MDMF模型中,实现9个结构参数的自适应最优化重构。增强模型设计的可解释性和泛化性,在避免模型主观经验构建的同时缩减了模型设计时所消耗的时间、人力等成本。

1 一维超声检测信号多域表征方法研究

通常对焊缝缺陷类型的诊断只利用采集到的一维超声检测信号进行分析,收集的数据样本均为一维时域序列,所包含的焊缝缺陷特征信息不明显且特征之间相关性表达不充分。为提高样本信息表达丰富性,开展一维超声检测信号多域表征方法研究,将一维超声检测信号映射入复数域和实数域的格拉姆角场域(Gramain angular field,GAF)[8]、马尔科夫转移场域(Markov transition field,MTF)[9]、递归域(recurrence plot field,RPF)[10]等高维空间域中。

1.1 复数域表征方法研究

将一维信号样本映射入复数域,其实部是信号本身的值,虚部是负变化率与角频率之比,将复数域的虚部信息引入共同作为特征向量避免了信息提取过程中的相位失配,提高了特征信息的完整性和有效性。Morlet复小波[11]具有良好的时频局部化特性,其小波系数的相位信息比较规则,因此本文使用Morlet复小波变换进行复数域映射。

设信号x(t)∈L2(R),根据小波变换的原理,将信号x(t)与小波基φa,b(t)进行卷积得到W(a,b),分别使用Real函数和Imagic函数对W(a,b)进行操作得到复数域的实部矩阵Re[W(a,b)]和虚部矩阵Im[W(a,b)]。具体如式(1)、(2)所示。

(1)

Re[W(a,b)]+jIm[W(a,b)]

(2)

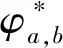
1.2 实数域表征方法研究

将一维信号样本映射入实数域即GAF、MTF和RPF等高维空间域中,以点、线、图像色彩或交叉边界等细节类描述来优化原始一维域中存在的特征单一性、相关性表达不充分等问题。实数域特征增强效果如表1所示。

表1 实数域特征增强效果图Tab.1 Real field feature enhancement rendering

GAF将时间序列在极坐标系统内进行编码,展现样本的不同信息粒度。在Gramain矩阵中的每个元素实际上是角度的三角函数值,衍生出两种不同的实现方式,即Gramain angular summation Field (GASF)与Gramain angular difference Field(GADF)。变换表达函数如式(3)与(4)。

(3)

(4)

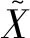
MTF是基于一阶马尔科夫链的变体,主要为解决马尔科夫转移矩阵对序列样本的时间特点的不敏感问题,转换时会优先考虑序列样本的时间位置关系。长度为n的信号序列X(t)将会被映射到每个对应的值域qj中,由qj结合每个样本紧邻的频率wij构建出相应的转移矩阵,继而由式(5)转换得到马尔科夫变迁域图像。

(5)

RPF是分析信号序列周期性、混沌性以及非平稳性的有效方法,可以分离出数据样本的内部结构、相似性以及预测性等相关知识。变换函数表达式如式(6)。

(6)

式中:Θ为Heaviside函数;ε为递归阈值。

2 面向焊缝缺陷检测的MDMF模型

为解决现有的实数域相位信息丢失、单一域焊缝缺陷特征信息不明显造成的焊缝缺陷类型检测模型准确率不高与现有模型高计算成本、高时间成本等问题。本文开展MDMF的研究。利用PSD特征提取器来提取复数域和两个实数域的深度特征,将提取的特征输入到多域多尺度焊缝缺陷深度特征融合空间,依据多域融合得到的有效特征实现不锈钢焊缝缺陷类型的高效识别。

2.1 深度半密集特征提取器

本文提出深度半密集特征提取器,包括多尺度深度可分离卷积和半密集连接[12]两个功能性模块,具体结构如图2所示,对选取出的两个实数域和复数域的特征域进行更深层次地特征提取,X∈{Xt,Xm,Xg},X表示经过特征提取器对某一焊缝缺陷问题提取到的综合特征,其中Xt,Xm,Xg分别为三个高维空间域所对应的特有特征,该方法丰富了一维缺陷信号的特征表征且更好地提取了不同域信息的内在关联性,得到更丰富的焊缝缺陷特征。为保证后续三个高维空间域特征融合操作的准确性及高效性,在特征输出时使用一维时间卷积层将特征控制在同一维度。

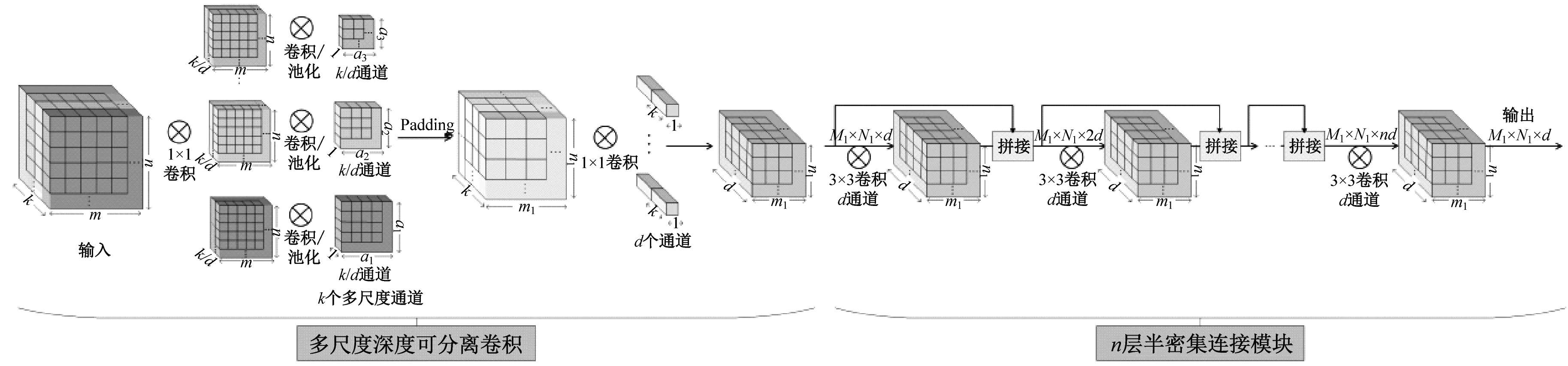
图2 深度半密集特征提取器Fig.2 Depth semi-dense feature extractor

多尺度深度可分离卷积模块在深度可分离卷积[13]的基础上被提出来,将深度卷积中的单一卷积核替换为多尺度不同大小的卷积核,扩大卷积感受野,有效提取不同尺度下的焊缝缺陷信息。

半密集连接模块基于特征重用的思想,对给定层的输出在后续层中被重用多次。给定层的输入不仅是来自上一层的输出,而且还是给定层之前的多个层的输出,可以有效避免梯度消失问题。较薄的密集网络要优于较宽的普通网络,提高了网络的参数效率。半密集连接模块的卷积层数与卷积核大小由第3章优化策略确定,其输入通道数分别为{d,2d,3d…nd},每一层的输出通道数均为d。

2.2 多域多尺度焊缝缺陷深度特征融合空间

为充分利用焊缝缺陷特征信息,MDMF拟考虑复数域和不同实数域在特征空间的关联与互补性,由基础CNN在单域上的诊断表现选取对相应数据集焊缝缺陷信息表征能力较强的两个实数域,将其与复数域共同作为特征域输入至多头注意力机制进行多域焊缝缺陷深度特征融合,构建出伴随有空间特性的特征融合空间。

MDMF将两个实数域分别作为两个特征Q,复数域实部矩阵作为特征K、V,使用多头注意力机制进行融合形成特征的实部,并将其与复数域虚部矩阵共同合成单一的复数矩阵作为复数焊缝缺陷深度特征输入复数全连接层进行分类,在融合过程中应用一种相对位置编码机制来实现状态重用,防止造成帧之间时间混乱。因使用多头注意力机制融合时需将特征图embedding[14]为一维序列,可能存在embedding后长度不同的问题,故本文通过Linear层将特征的长度转换,使其长度相同,在运算过程中必须保持embedding的长度可以整除复数多头注意力机制中头的个数。若遇到embedding为质数无法整除的情况,需将其填充0后再进行计算,并在运算结束后删除补0位置的信息。在最终两个融合部分空间特征的拼接上采用哈达玛乘积操作如式(7),区别于传统的concat以及add方式,哈达玛乘积操作可以对特征张量的时间步长信息进行保留。第i个头部的注意力如式(8)～(9)所示,复数全连接层计算为式(10)。

rept=[αt;βt;αt·βt]Wrep+brep

(7)

(8)

(9)

(10)

CReLU(W)=ReLU(Wr)+iReLU(Wi)

(11)

3 基于分组通信改良的莱维混沌平衡优化器算法

平衡优化器(equilibrium optimizer,EO)算法是由Faramarzi[15]于2020年提出的一种受控制容积强混合型动态质量平衡的物理启发式优化算法,具有需调节参数少、稳定性好等特点,目前已成功应用于约束优化问题[16]、多模态图像配准[17]等现实问题中。具体算法原理是控制体积-质量平衡模型中,粒子根据平衡候选解进行浓度更新,最终达到平衡状态。主要为种群初始化、平衡池构建和浓度更新三个阶段。更新公式如式(12)～(17)所示。

Ci=LB+Ri*(UB-LB)

(12)

(13)

Ceq,pool={Ceq1,Ceq2,Ceq3,Ceq4,Ceq(ave)}

(14)

(15)

F=a1sign(r-0.5)[e-lt-1]

(16)

(17)

式中:Ci为初始种群中第i个粒子的初始位置;Ri为[0,1]中i=1,2,…n的随机向量;UB和LB分别为搜索空间的上界和下界;Ceq1～Ceq4和Cave为当前最好的四个候选解以及它们的算术平均值共同构成平衡池Ceq,pool;C和Ceq为当前粒子和平衡候选解;λ和r为[0,1]之间的随机向量;V为单位体积;G为生成率。F为指数项。Iter和Max iter分别为粒子的当前迭代次数和最大迭代次数。a1与a2分别设置为2和1。

EO中初始个体都是在搜索空间内随机生成,难以获取较好的种群多样性,易导致算法出现收敛性能差、局部开拓能力弱等问题。对此PEO算法依次引入莱维飞行初始化、混沌浓度更新以及分组通信策略三种方式提高初始解的质量,扩大搜索区域,增强算法的全局以及局部搜索能力,构成面向卷积神经网络多维超参数自寻优的PEO模型优化策略。

莱维飞行[18]是服从莱维分布的随机搜索路径,是一种短距离搜索和偶尔长距离搜索相间的随机行走模式,可以有效提升EO种群的全局搜索能力,避免迭代后期种群中所携带的待优化参数多样性降低。结合莱维飞行具有随机性和规律性的特点来初始化种群。莱维飞行表达式如式(18)所示。将原种群初始化式(12)改进为式(19)且由于莱维飞行十分复杂,目前大多使用Mantegna算法,如式(20)～(22)所示,故式(19)可简化为式(23)。

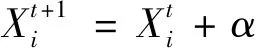
(18)

Ci=LB+Levy(β)*(UB-LB)

(19)

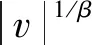
(20)

(21)

(22)

Ci=LB+s(u,v)*(UB-LB)

(23)

混沌映射[19]拥有非周期、不收敛和有界等特点,可以有效避免根据单一候选解进行浓度更新导致种群多样性流失致后期陷入局部最优的问题。在求解高维复杂问题时,标准EO的种群多样性随算法迭代而逐渐减小,故本文将Circle混沌映射融入浓度更新策略来解决多样性流失的问题。Circle映射表达式如式(24)。

(24)

式中:α为0.5;β为0.2;Xi+1为混沌序列中第i+1个粒子。将Circle混沌映射向量化后与原浓度更新公式(18)相结合,得到混沌浓度更新公式如式(25)。

(25)

分组通信策略将种群分为四组,各组独立更新,采用三种通信策略进行组间信息交换以缓解各组信息差等问题,提高了搜索能力和收敛速度,扩大了搜索区域,能更快找到最优解且避免陷入局部最优。

PEO算法三种通信策略具体如下所示:

策略一:将所有粒子分为N组,每组为二进制数。平均数量相差一位数的两组为最优平衡候选组,当前组中一些适应度值较差的粒子发生个体突变。

策略二:该策略对所有群体的全局最优值进行排序。第一组中排序后的最佳粒子替换第二组中适应度较差的粒子,第二组中的最佳粒子替换第三组中适应度较差的粒子,以此类推。最后一组用适应度值较差的粒子取代了第一组中的一些粒子。

策略三:每20代使用通信策略一,每50代使用通信策略二循环更新。

4 MDMF模型自优化

MDMF卷积模型中,卷积层结构的灵感来自于文献[20]中用于焊缝表面缺陷分类研究。但值得注意的是,此类模型大多是基于人工经验而选择的模型,确定内部参数时均依靠大量的专家经验来调试,并且由于焊缝缺陷数据采样形式的差异性,面对不同的问题很可能需要重构模型。对此本文在原EO的基础上,结合多策略优化并引入群通信思想提出了一种基于分组通信策略改良的莱维混沌EO模型优化算法(PEO),具体优化步骤如算法1所示。

经上述机制改良后的PEO将用于MDMF中9个关键参数自寻优,以减小模型设计难度同时提高模型自适应寻优能力,得到优化后的焊缝缺陷类型检测模型AMDMF。9个参数包括半密集连接模块卷积层数、学习率、批次大小、三个卷积层各自的激活函数、优化器、半密集连接模块卷积核大小和多头注意力机制头个数。根据经PEO每个粒子位置信息建立AMDMF模型,训练AMDMF模型并利用式(26)的适应度函数计算它在测试集上的性能。式中y(i)代表预测标签,t(i)为真实标签,batch为批量大小。求取出的f作为PEO中的适应度函数进行种群更新,最优个体信息会被用来建立最终的模型。

(26)

算法1 PEO算法流程

-----------------------------------------------

输入:Particles(种群大小),Max_iter(最大迭代次数),Dim(维度)

输出:Total Best(全局最优值)

初始化:G(生成速率),Particles(种群大小),P(每组种群数),Iter (当前迭代次数),Max_iter(最大迭代次数),a1,a2(勘探和开发能力).

1:for gth = 1 toNdo

2:随机更新P = Particles/N.

3:end for

4:while Iter <= Max_iter do

5:采用其中一种通信策略更新粒子.

6:for gth = 1 toNdo

7:fori= 1 to P do

8:计算每组粒子适应度值.

9:寻找每组中当前四个最好的候选解.

10:end for

11:将当前最好解作为Total Best.

12:根据公式(13)计算四个最好候选解的均值.

13:根据公式(14)构建平衡池.

14:根据公式(17)计算t.

15:fori= 1 to P do

16:从平衡池中随机选择一个候选解.

17:根据公式(25)更新粒子浓度.

18:end for

19:end for

20:Iter = Iter + 1

21:end while

5 试验与结论

5.1 试验平台环境搭建、数据采集与预处理

本文试验在Intel Core CPU I5-10500H、16 GB内存、64位Windows操作系统、PyCharm2020.1.3,并使用自制数据集。通过与山西省机电设计研究院有限公司合作,在该单位搭建试验平台(图3),制备包含夹渣、裂纹、气孔、未焊透、未熔合五类缺陷类型的试样。使用KARL DEUTSCH(ECHOGRAPH)探伤仪、Tektronix DPO 2024B示波器和2.5P 9x9 K2.5斜探头对缺陷试样进行数据采集。试验共采集了未熔合、夹渣、未焊透、裂纹和气孔五种超声A扫缺陷数据544条。

图3 试验平台Fig.3 The experiment platform

图4(a)为采集到的一维超声检测信号可视化图像,电磁耦合的起始时刻作为超声信号发射初始时刻,使用巴特沃斯滤波器进行滤波处理,得到图4(b)所示的图像。通过向无损检测领域专家进行咨询,缺陷信号可以在一次回波和二次回波时间范围内被全部采集到,因此为了避免电磁耦合信号对缺陷信号特征提取造成干扰,并保证不遗漏一维回波信号,本文分别将第一次与第二次回波对应的时间点作为起点和终点对一维超声检测信号进行截取,得到如图4(c)所示的时域数据。

(a) 原始一维检测信号可视化图像

将处理后的一维时域信号分别映射至复数域以及实数域,完成一维超声检测时域信号的多域衍生。对通过多域转换得到的各高维空间域二维图像进行相同旋转、翻转、镜像和平移等数据增强操作,为训练深度学习模型提供了一定的数据支撑以达到较好效果。各高维空间域数据集经此操作后均由544张扩充至8 160张,包含夹渣、气孔和未焊透缺陷各1 590张、裂纹1 815张、未熔合1 575张,并按照4∶1的比例划分训练集和验证集。

5.2 PEO算法性能验证

为验证PEO相较近几年其他智能优化算法的优越性,对麻雀搜索算法(sparrow search algorithm,SSA)、蜻蜓优化算法(dragonfly algorithm,DA)、灰狼优化算法(grey wolf optimizer,GWO)、粒子群优化算法(sunflower optimization,SFO)、平衡优化器算法(equilibrium optimizer,EO)五种算法在12个基准函数上进行对比仿真试验。12个基准函数包括:Sphere(F1)、SchwefelN2.22(F2)、SchwefelN1.2(F3)、SchwefelN2.21(F4)、Rosenborck(F5)、Step(F6)、Quartic(F7)七个高维单峰基准函数,以及Schwefel(F8)、Rastrigin(F9)、Ackley(F10)、Griewank(F11)、Penalized(F12)五个高维多峰基准函数。

各算法的种群规模设为100,最大迭代次数设为1 000,问题维度为30,初始参数值参照各算法原始论文的设置。为避免寻优结果的偶然性并证明PEO的稳定性,选取各基准函数独立运行30次的试验结果作为试验数据,将各个算法的平均值(Mean)和标准差(Std)作为最终评价指标,较优结果用粗黑体进行表示,单峰多峰基准函数对比结果分别如表2和表3所示。

表2 单峰基准函数试验结果Tab.2 Experimental results of single peak reference function

表3 多峰基准函数试验结果Tab.3 Experimental results of multi-peak reference function

由表2分析可知,在相同测试约束条件下,PEO对五组高维单峰基准函数的统计结果明均显优于其它5种对比算法。对于基准函数F1、F2、F3、F4,PEO均能稳定得到其理论最优解。在求解F5、F6和F7时,虽然PEO未能寻找出理论最优解,但在平均值和标准差两个评价指标上相比其它算法优越多个数量级。证明经改进后的PEO相较于其他算法能够在单峰类函数上具备较强性能和稳定性。

由表3分析可知,对高维多峰基准函数F9、F11,PEO与SSA均可稳定收敛于全局最优值。在F8、F10基准函数上,相较其它算法,PEO比其他算法有着显著的提高与优越性。在求解F12时,PEO在两项评价指标上略差于SSA,但很大程度上优于其他对比算法。因此,不论在单峰基准函数或是多峰基准函数上,PEO在多次寻优过程中,均能表现出较好的寻优性能。表明PEO具备高效的全局寻优能力和局部探索能力,能够充分高效的探寻搜索空间,且稳定性和鲁棒性较强。

由于本文对EO算法的修改较为深入,可能会出现引入的修改会带来性能下降的问题,为避免该问题,本文对EO算法的修改进行了详尽的消融试验以证明修改的可行性和正确性。PEO改进消融试验结果见表4,表中结果均为不同算法在12个基准函数运行30次的平均适应度值。

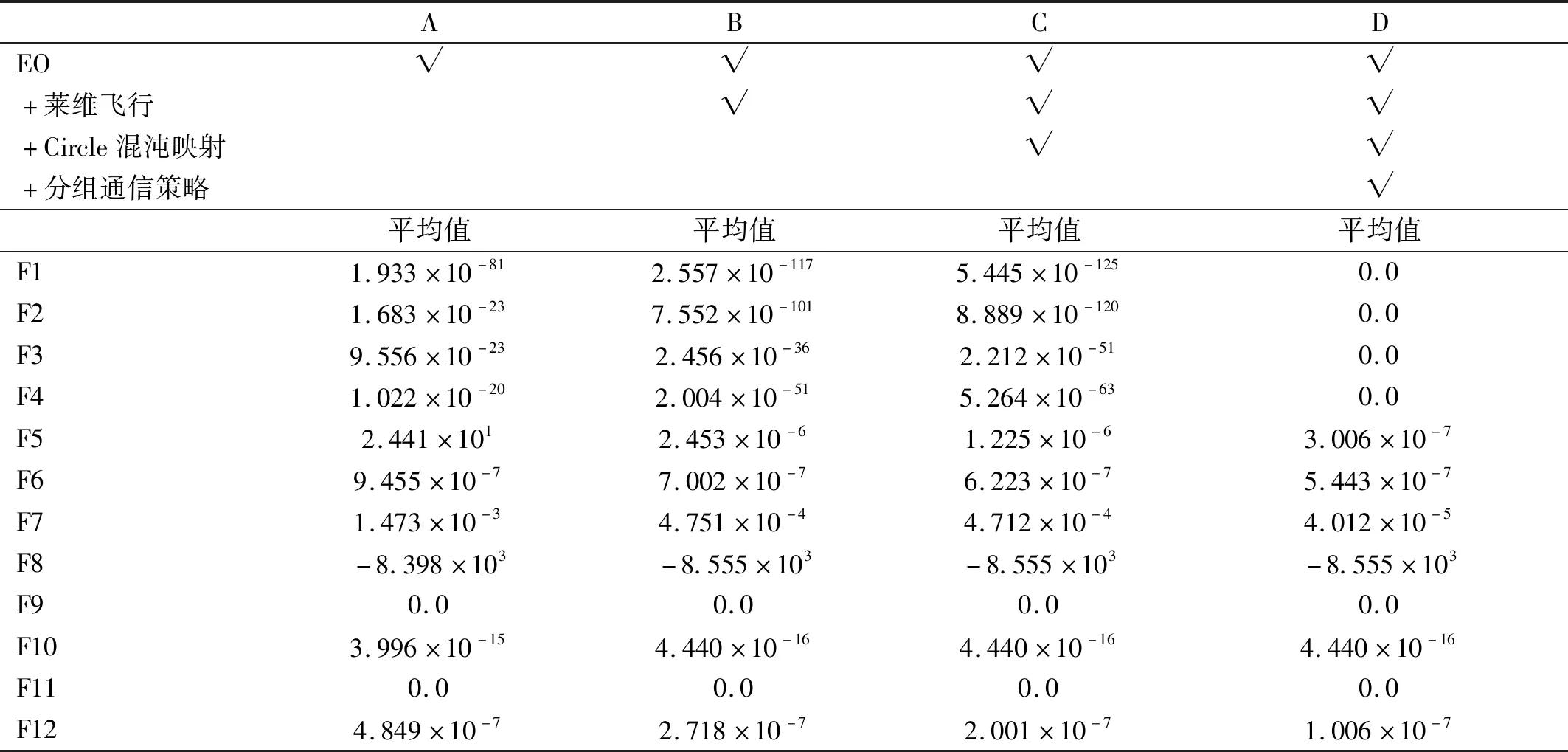
表4 PEO改进消融试验Tab.4 PEO modified ablation experiment

从消融试验中可以得出本文每次修改后的算法寻优效果对比原算法均有不同数量级的大幅提高,证明了PEO引入的各个改进策略均可以提高算法的寻优性能,且尤其引入分组通信策略后提高最高,在多个适应度函数上均搜索到理论最优解。因此该算法可以应用于本文对MDMF的自适应寻优问题中且具有较大的实用价值。

5.3 高维空间域的选取及有效性验证

为了验证缺陷样本高维空间域转换有效性,并选取出在不锈钢焊缝缺陷检测中表征能力最好的两个实数高维空间域。使用目前主流的轻量型网络MobileNetV1、MobileNetV2、MobileNetV3、ShuffleNet、SqueezeNet在原数据集上进行检测精度的比较,具体对比结果如图5所示。

图5 候选实数域在不同网络下检测精度对比图Fig.5 Comparison of detection accuracy of candidate real number fields in different networks

综上结果分析,在同一网络中,相较于时域方式,GASF、GADF、RPF和MTF各实数域映射方式取得的平均精度均有提升,证明了本文域转换方式的先进性。为将实数域之间的优势相结合,更好的应用于本文研究方法。选取上述验证试验中平均精度处于第一、二位的MTF和GADF作为2.1节所述特征融合空间的两个实数域输入。

5.4 MDMF模型参数自优化

本文利用经试验验证后的高性能PEO对MDMF模型自适应寻优,将个体的9个维度分别对应于模型MDMF的9个待定参数:半密集连接模块卷积层数、学习率、批次大小、三个卷积层各自的激活函数、优化器、半密集连接模块卷积核大小、多头注意力机制头个数。初始种群数量设置为10,最大迭代次数设置为5。基于此,构建优化后的模型AMDMF。

PEO的参数搜索范围如表5所示,使用PEO所搜寻到的最优模型(表6)与其他基线模型进行对比,在每种情况下,较优结果都用粗体号突出显示。

表5 MDMF模型待优化参数及范围Tab.5 Parameters and range of MDMF model to be optimized

表6 MDMF模型使用PEO优化后的最优模型组件Tab.6 The MDMF model uses PEO optimized optimal model components

为了充分证明本文所提方法的有效性,将SqueezeNet、MobileNetV3、ShuffleNet、MDMF与本文自适应构建的高性能AMDMF模型从参数量、时间消耗和准确率等不同角度进行比较,结果如表7所示。从表7可以看出,AMDMF相比MDMF在准确率提升2.48%的前提下,参数量、训练时长和时间消耗均大幅下降,证明了本文所提基于PEO的模型自优化方法的有效性,且AMDMF优于所有基线模型。AMDMF较性能优秀的MobileNetV3模型在准确率仅有4.74%上升情况下大幅减少了模型参数量以及时间消耗且单幅图像的检测时间仅为1 ms,可满足不锈钢焊缝缺陷在线实时识别的要求,能够为集成和便携设备的开发提供技术支持。

表7 网络模型性能对比试验Tab.7 Network model performance comparison experiment

混淆矩阵进一步展示了高性能AMDMF模型在测试集中对每个类别缺陷的识别效果,如图6所示,标签序号0～4分别代表夹渣、裂纹、气孔、未焊透、未熔合五类缺陷。从图中可以看出,模型对裂纹、未焊透、未熔合三类类缺陷有较高的识别率,分别为99.1%、97.5%、和96.7%。对夹渣和气孔两类缺陷的识别准确率略低,均为94.7%,造成这两类缺陷识别准确率较低的主要原因为夹渣缺陷是熔渣焊后残留在焊缝中形成缺陷,导致部分超声波会穿透这些熔渣到达钢板底部,损失部分缺陷信号,而部分气孔缺陷的位置靠近钢板底部,在利用超声波对焊缝缺陷检测过程中,二者易被混淆。

图6 混淆矩阵Fig.6 Confusion matrix

5.5 AMDMF模型泛化能力验证

我们选择了两个公共数据集NEU-CLS[21]和miniImageNet[22],来验证所提出的网络和方法的泛化能力,NEU-CLS是东北大学发布的热轧带钢表面缺陷图像数据集。缺陷包括裂纹 (Cr)、夹杂物(In)、斑块(Pa)、点蚀表面(PS)、轧制氧化皮(RS)和划痕(Sc)。该数据集由六种缺陷的1 800张灰度图像组成,每个图像以300个样本为例。miniImageNet是由DeepMind团队从包含2万多个类别(如“气球”、“轮胎”和“狗”等且每个类别均有不少于500张图像)的ImageNet数据集中提取而成的数据集,包含100个类别,共计60 000张彩色图像,每个样本像素值均为84×84。两个数据集分别按照4∶1的比例分为训练集和测试集,在AMDMF上进行训练。测试集的分类准确率如图7和图8所示。在NEU-CLS数据集上,AMDMF达到了98.52%的分类准确率;在miniImageNet 数据集上,AMDMF的分类准确率达到了84.31%。试验结果表明,本文所提出的方法不仅可以用于缺陷识别,而且对其他领域的复杂分类任务也具有一定的应用价值,并具有一定的泛化能力。

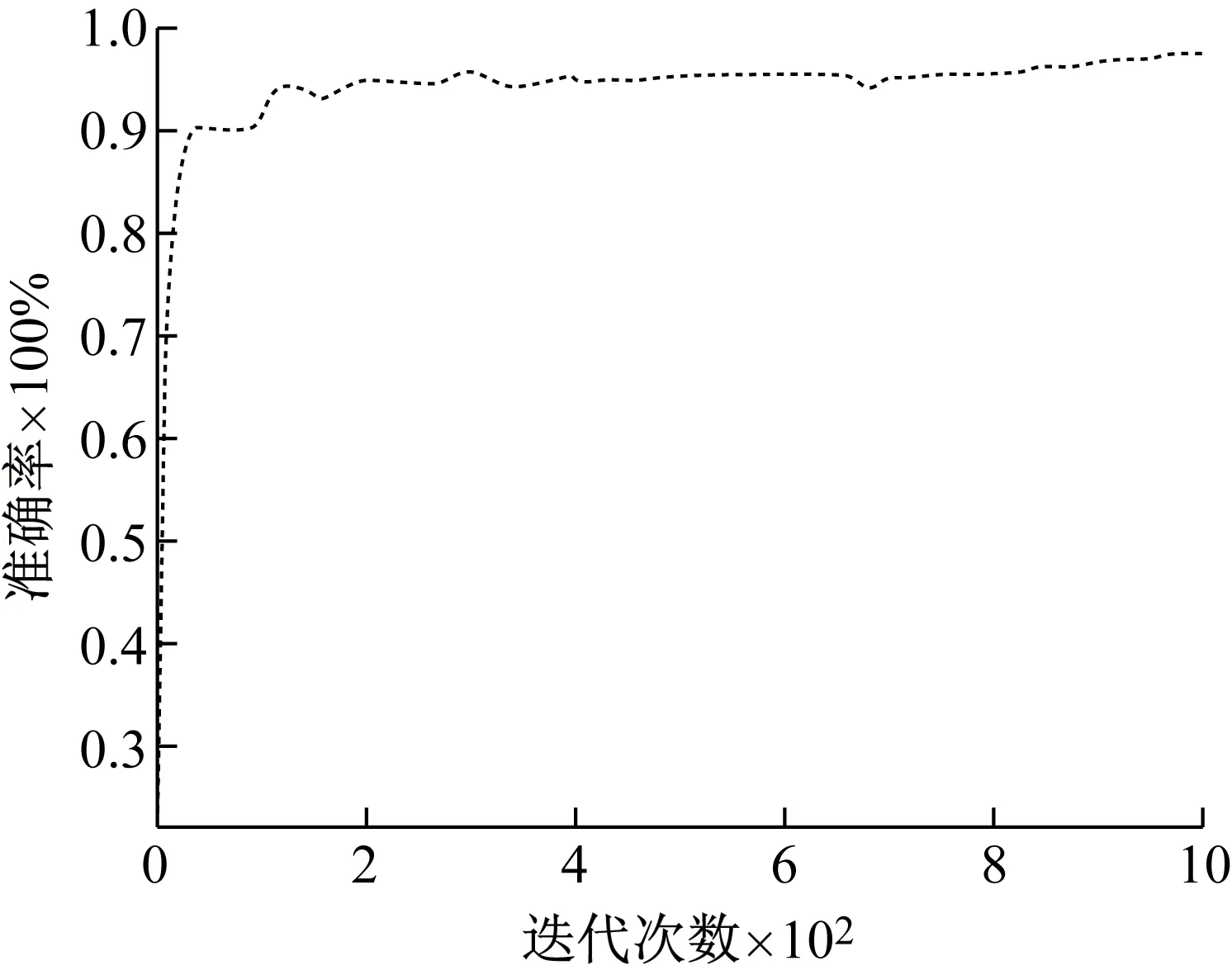
图7 NEU-CLS数据集上的分类准确率Fig.7 NEU-CLS dataset classification accuracy

图8 mimiImageNet数据集上的分类准确率Fig.8 MimiImageNet dataset classification accuracy

6 结 论

在这项研究中,我们提出了一种基于多域多尺度深度特征自适应融合的焊缝缺陷检测。通过试验分析比较,可以得出以下结论。

(1) 基于不锈钢焊缝超声检测信号开展智能化缺陷识别是具备可行性的。

(2) 将一维超声检测时域信号映射至复数域以及GAF、MTF、RPF等实数域中,由基础CNN在单域上的诊断表现选取对相应数据集焊缝缺陷信息表征能力较强的两个实数域与复数域进行多域多尺度焊缝缺陷深度特征融合,有利于找到在焊缝检测领域契合度更高的高维空间域数据集的组合。

(3) 开展面向卷积神经网络多维超参数自寻优的PEO模型优化策略对模型结构自适应压缩和参数自适应优化,可以在不损失网络精度的前提下大幅减少网络的参数量和计算量,有效确定针对特定任务的最优参数组合,避免人为调参带来的高时间成本和高计算成本。

通过多域多尺度特征融合和模型自优化,我们所设计的AMDMF模型相比其他基线模型各项指标明显提高,对五类不锈钢焊缝缺陷的识别准确率为96.54%,对单个焊缝缺陷类型识别时间为1.0 ms,可满足不锈钢焊缝缺陷在线实时识别的要求,这为实际工程应用中基于超声检测方法开展自动缺陷识别提供了一定的技术参考,为后续集成辅助诊断设备提供有利的技术保障。我们所提出的方法还具备一定的泛化能力和可靠性,除了基于序列样本的各种识别、分类、诊断和检测模型外,还可以广泛用于各种网络模型的自适应压缩和优化。我们在该领域的未来研究将侧重于多目标检测和识别,并在时间复杂度和识别性能之间取得平衡。