改进小波阈值函数和ACEWT方法的滚动轴承故障声发射信号特征提取
2023-09-20杨学广梁哲铭
于 洋,李 赟,杨 平,杨学广,梁哲铭
(1.沈阳工业大学 信息科学与工程学院,沈阳 110870;2.中国航发燃气轮机有限公司,沈阳 110168;3.中国航空工业集团公司 沈阳飞机设计研究所,沈阳 110035)
滚动轴承是旋转机械中最常用的零部件之一,也是旋转机械系统中的易损件之一[1]。据统计,旋转机械故障中轴承占比约为30%[2],严重缺陷或损伤往往会导致设备的损坏,造成经济损失。因此,对滚动轴承采取有效的故障诊断十分重要。
声发射信号灵敏度高、可实现轴承故障的早期诊断,本文采用声发射技术监测滚动轴承的故障信息。声发射技术比振动方法可以更早的获取滚动轴承故障特征。声发射信号以其信号频率高、不受结构和旋转动态振动噪声的影响等优点[3],被广泛应用。但早期的故障声发射信号易受环境噪声的影响,信噪比低,使有用的声发射信号被淹没,从而难以对故障进行有效的分析与诊断。如何提取低信噪比声发射信号中故障频率特征,一直是声发射技术监测设备健康状态与故障诊断的难点。
近年来,国内外学者应用小波变换(wavelet transform,WT)、经验模态分解(empirical mode decomposition,EMD)、变分模态分解(variation modal decomposition,VMD)的方法对轴承故障信号进行分析,但这些常用的方法会有一定的不足:WT方法受小波基的限制,缺乏自适应性;EMD方法存在模态混叠,计算量较大;VMD方法在分解分量个数时需要根据经验设置等问题[4-6]。Gilles[7]提出的一种新的构建自适应小波的方法——经验小波变换(empirical wavelet transform,EWT),EWT方法弥补了以上常用方法的不足,具有独特的优势。李志农等[8-10]采用经验小波变换方法对旋转机械,风力发电机进行了分析;王晓龙等[11]提出改进经验小波能量阶次谱的诊断方法。
工程上,机械设备复杂,轴承故障声发射信号在传递过程中故障信号要经过多个结合面造成信号衰减,并受到噪声等方面的干扰,导致声发射信号的信噪比低,轴承故障声发射信号微弱。此时,轴承故障声发射信号应用EWT方法提取故障频率特征困难,因此利用自相关运算结合经验小波变换方法来突出轴承故障弹性波强度的同时,需对采集的声发射信号进行降噪预处理。
目前,李红延等[12]提出了改进小波阈值函数方法;周风波等[13]根据Donoho阈值消噪原理,采用提升小波变换的阈值改进算法;向北平等[14]提出了一种样本熵的改进小波包阈值去噪算法;杨铮等[15]采用对数逼近函数改进阈值算法;李树勋等[16]根据指数函数改进小波阈值降噪方法;Srivastava等[17]提出基于分解层数的降噪方法。尽管许多文献大量研究信号降噪的问题,但这些小波阈值函数降噪方法都是面对振动信号而提出,根据声发射信号特性降噪的很少。声发射信号具有冲击性且快速衰减的特点,根据此特点,提出了改进小波阈值函数降噪(即衰减正弦型与指数型的小波阈值函数降噪法),更适用于低信噪比声发射信号进行降噪预处理。
在低信噪比下,本文针对经验小波变换方法对轴承故障声发射信号频率特征难提取问题,结合声发射信号特点、自相关运算和经验小波变换方法各自的优势,提出了改进小波阈值函数和ACEWT方法。将所提方法与EWT、改进小波阈值函数-EWT、MCKD-EWT方法进行对比研究,并应用到滚动轴承的故障诊断中,通过试验结果验证了所提方法的有效性,实现低信噪比下,滚动轴承故障声发射信号频率特征提取。
1 改进小波阈值函数-ACEWT方法
1.1 改进小波阈值函数降噪研究
故障声发射信号的理想模型函数是一个衰减正弦波[18],即:
x(t)=A0exp(-αt)·sin(2πf0t)
(1)
式中:A0为信号初始幅值;α为材料阻尼;f0为信号频率。根据声发射信号的衰减特性,调整衰减函数的因子,提出衰减正弦型与指数型的小波阈值函数。改进小波阈值函数的表达式如下:

(2)
式中:wn为声发射信号在第n层分解的小波系数;λn为每层小波系数所对应的阈值。当|wn|≥λn时,为了逼近真实的声发射信号特征,提出衰减正弦函数进行降噪;当|wn|<λn时,声发射信号中噪声占比较大,采用指数型函数降噪。u为阈值函数的调整因子,当u趋近于1时,改进的阈值函数近似于硬阈值函数;当u趋近于0时,改进的阈值函数近似于软阈值函数,改进的阈值函数具有连续性;因此u的取值范围为(0,1]。改进的阈值函数既保留了硬软阈值函数的优点,又克服了不足,同时对小波系数保留有用的声发射信息,具有较好的去噪效果,ξ为常数0.02。
声发射信号的小波系数在每一层分解尺度上都有所不同,会随着分解尺度的增大而减少,但是传统的阈值选取方法并没有充分考虑分解尺度对阈值的影响,因此本文采取式(3)的阈值选取方式。假如声发射信号x(t)进行小波分解,则每层小波系数所对应的阈值λn的计算[19]表达式为
(3)
式中:σn为第n个小波系数噪声标准差;N为信号长度。噪声标准差[20]σn如下
(4)
使得阈值随着分解尺度增加而减小,满足了声发射信号的小波系数随分解尺度增大而减小的特点,使其具有自适应性特点,具有更好的降噪效果。
1.2 ACEWT方法提取轴承故障特征研究
损伤的轴承在运行时,会引起接触面的弹性波冲击而产生声发射信号,此时的声发射信号频散特性复杂,模态个数多,呈非线性与非平稳性特点。EWT方法融合了经验模态分解方法的自应适分解理念和小波变换理论的紧支撑框架,非常适用于滚动轴承故障声发射信号。ACEWT方法是自相关运算与经验小波变换方法的结合,对待分析信号先进行自相关运算,后进行经验小波变换。
1.2.1 经验小波变换
EWT方法通过检测频域内的极大值点对信号的Fourier谱进行自适应的划分,并对划分得到的每个分段构建相对应的小波滤波器。首先将Fourier谱定义在[0,π]的区间范围内,并检测频域内极大值点所在位置,取相邻两个极大值点的中点作为各分段的边界点ωn,以此为依据将信号分为n段,其中ω0=0,ωn=π。每个分段可以表示为[Λn-1,Λn],根据Meyer小波的构造方法对每个分段加小波窗,得到经验尺度函数Φn(ω)和经验小波函数Ψn(ω)
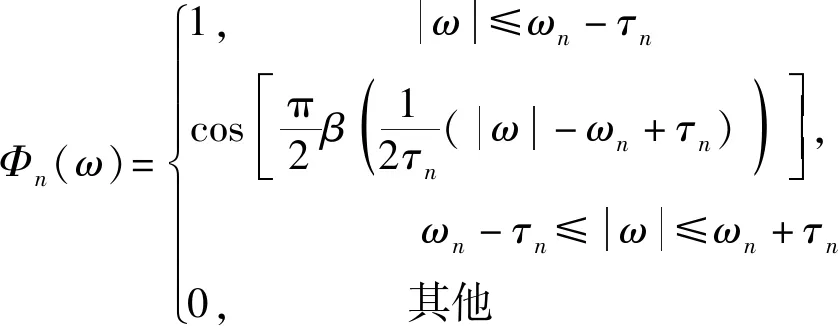
(5)

(6)
其中β(x)为[0,1]内任意满足K阶导的函数,一般选取[21]为β(x)=x4(35-84x+70x2-20x3),τn=γωn,0<γ<1。为了得到紧支撑频率框架,参数γ应满足式(7)
(7)
根据构造经典小波变换的方法构造经验小波变换,其中细节系数和近似系数分别如式(8)、式(9)所示
(8)
(9)
可以得到经验模态函数的定义如下
(10)
(11)
原始信号重建过程如下
(12)
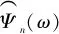
经验小波变换方法的关键在于对频谱的自应适分割,合理的分割频谱会直接影响对信号的分解效果。Gilles提出自动确定频谱极大值数量N,通过调整参数能够得到合适的N。李志农等通过预先观察待分析的信号频谱来确定合适的N,随后将检测到的极大值降序排列取前N个,对频谱进行分割。本文根据李志农等方法对声发射信号进行设置分量数目。
1.2.2 自相关运算
自相关运算可用于检测混淆在随机信号中的周期成分。因此,滚动轴承故障声发射信号进行自相关运算,可以增强轴承故障周期性弹性波冲击强度。
(13)

1.2.3 经验小波能量比-熵指标
(1) 经验小波能量比
经验小波变换中各节细节系数能量比表征各节细节系数在轴承声发射信号中所占能量的相对关系,若能量比值较大时,说明此阶细节系数包含较多的轴承故障信息,计算各阶的细节系数能量比为
(14)
式中:fi(t)为经验小波变换的第i层细节系数;n为经验小波变换中细节系数的个数,利用能量比指标筛选细节系数,对信号的重构具有一定效果。但能量比指标易受噪声的影响。
(2) 经验小波能量比-熵
为了克服经验小波能量比指标受噪声影响的不足,更好地筛选细节系数,强化重构信号中的轴承故障信息。应用经验小波能量比与经验小波能量熵结合(即经验小波能量比-熵)指标进行最优fi(t)分量筛选。经验小波能量熵值大小表示经验小波系数有序无序程度。对于损伤的轴承在运行时,会产生周期性的弹性波冲击,分解得到的细节系数弹性波脉冲若有序,则经验小波能量熵值越小,包含轴承故障信息越多。根据信息熵的思想,经验小波能量熵[22]可以定义为
(15)
式中:Ji为第i个细节系数的能量占总能量的比值,总能量是未经过ACEWT分解的信号能量;n为经验小波变换中细节系数的个数。

1.3 方法步骤
步骤1滚动轴承故障声发射信号x(t)通过改进小波阈值函数去噪。
步骤2将去噪后的声发射信号进行ACEWT方法分解,得到各阶经验小波细节系数和近似系数。


本文方法流程图如图1所示。
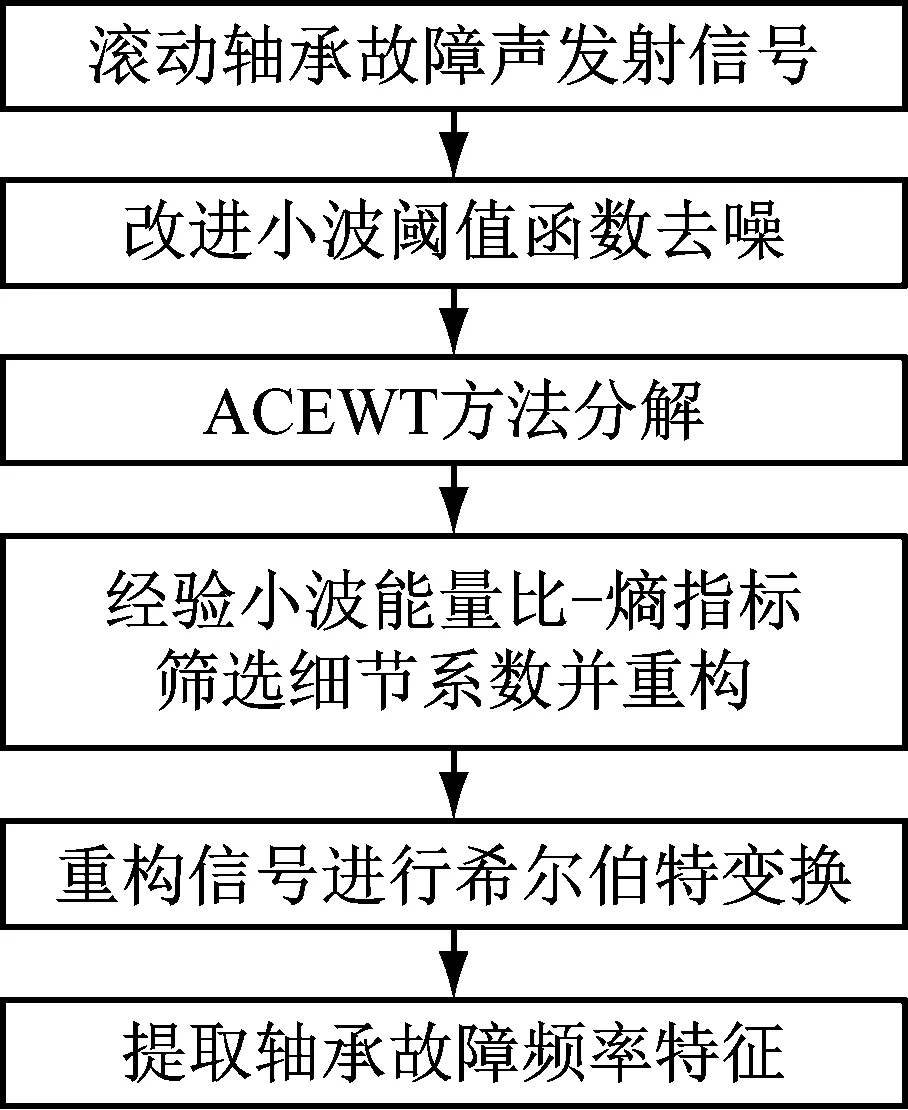
图1 本文方法流程图Fig.1 Flowchart of this article
2 仿真研究
模拟滚动轴承外圈故障产生的信号y(t)来进行讨论。为了还原真实效果,加入高斯白噪声n(t),Y(t)为含噪故障信号,故仿真信号为
y(t)=0.05sin(2π×1 000t)e-2π×80t
(16)
Y(t)=0.05sin(2π×1 000t)e-2π×80t+n(t)
(17)
仿真信号选用采样频率为1 MHz,采样长度500 001个点,分别对无噪声轴承故障仿真波形(见图2(a))和含噪声SNR=-25 dB的滚动轴承故障仿真波形(见图2(b))进行FFT频谱分析,FFT频谱分别如图3(a)、图3(b)所示。由图2(a)可知,外圈故障时间间隔为31 ms。由图3(a)可以得出滚动轴承外圈的故障频率为32 Hz。由图2(b)、图3(b)和图3(c)可知,含噪声的轴承故障仿真波形、频率特征已被噪声所覆盖,已分析不出故障频率。

(a) 轴承故障信号
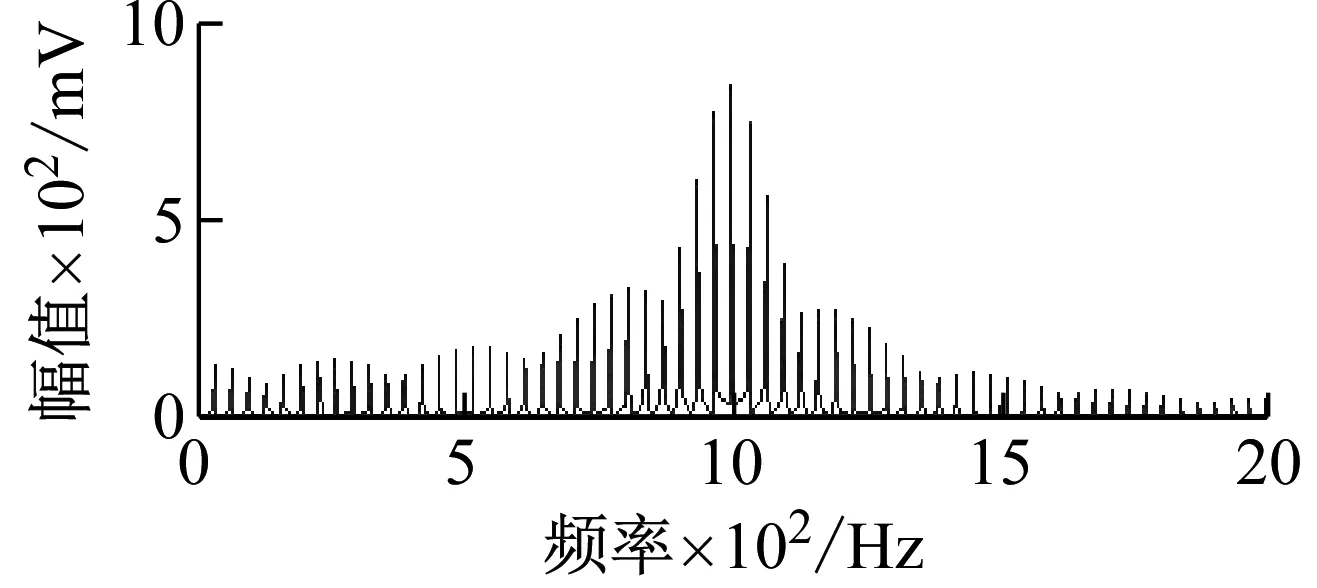
(a) 轴承故障频谱
2.1 改进小波阈值函数降噪分析
图3(c)中故障频率被噪声已覆盖,因此对图2(b)仿真信号进行降噪分析。由于声发射信号具有冲击性及快速衰减的特点,在小波分解中要求小波函数既有较短支集,亦有较高消失矩,以及一定正则性,Db8小波基函数与声发射信号较为相似,故选用Db8小波基函数进行小波分解。仿真试验经反复试算取分解层数为4层,分别采用硬、软阈值函数、本文阈值函数以及文献[12]中的方法,对仿真加噪的轴承信号进行降噪。本文阈值函数法参数选取为u=0.1。各阈值函数降噪后的波形如图4所示。从图4(c)中可以观察出冲击信号,相对于图4(a)、图4(b)及图4(d)较为明显,图4(d)中虽然也能观察出冲击信号但噪声较大。

(a) 硬阈值函数
为了对比以上四种去噪方法,本文通过信噪比、均方根误差2种性能指标对信号的去噪效果做定量分析,信噪比越大,均方根值误差越小,降噪效果越好。阈值函数去噪后的性能指标如表1所示。
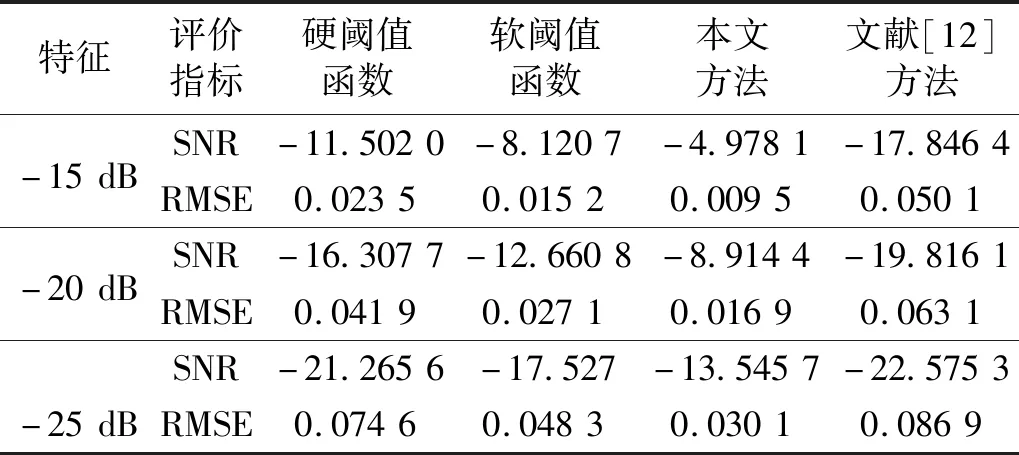
表1 各阈值函数去噪对比结果Tab.1 Different threshold method denoising comparison results
表1中分别列出SNR=-15 dB、SNR=-20 dB和SNR=-25 dB三种不同的低信噪比情况。对于 SNR=-25 dB可看出,改进的阈值函数对比硬、软阈值函数以及文献[12]阈值函数分别提高了7.719 9 dB、3.981 3 dB和9.029 6 dB;RSME分别降低0.044 5、0.018 2和0.056 8,表明改进小波阈值函数具有良好的降噪效果。纵看三种不同的信噪比,改进小波阈值函数在上述不同信噪比情况下分别提高10.021 9 dB、11.085 6 dB和11.454 3 dB,表明本文所提的改进小波阈值函数在低信噪比中效果更好。
不同取值的调节因子u,对去噪后信号的性能指标变化趋势如图5(a)、图5(b)所示,图5(a)为调节因子u值对信号降噪后SNR的变化,图5(b)为调节因子u值对信号降噪后RMSE的变化。从图5(a)、图5(b)中可知,u值越接近于1,降噪后信号的SNR越低、RMSE越大;u值越接近于0,则相反。同u值条件下,信号信噪比越低,降噪后信号的SNR提升越大、RMSE越小,表明本文改进的小波阈值函数降噪有效,并更适合应用于低信噪比信号。
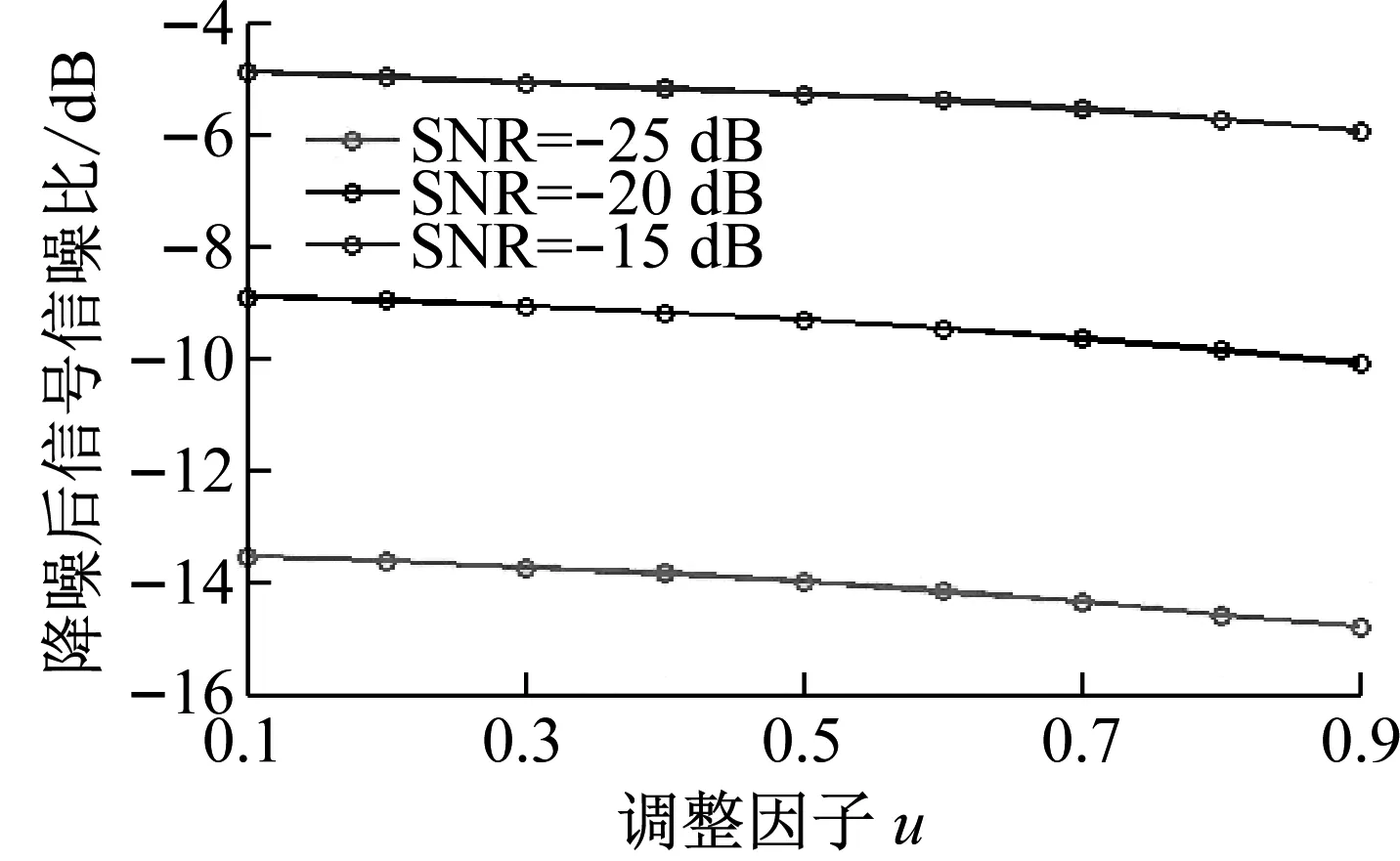
(a) 调节因子u选取对信号降噪后SNR影响
2.2 ACEWT方法提取故障特征
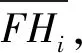

图6 重构细节系数分量Fig.6 Reconstruct the optimal component
由图6可知,出现了以0.031 s为间隔的外圈故障冲击脉冲,冲击脉冲前0.4 s比较明显,故障冲击脉冲突出。对重构信号做希尔伯特包络谱分析,结果如图7所示。由图7可知,可准确得出故障频率及其倍频,故障频率为32 Hz。
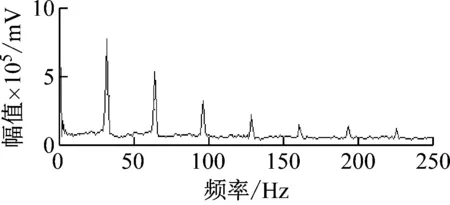
图7 改进小波阈值函数-ACEWT方法Fig.7 New method
由式(17)得到仿真轴承故障信号,直接通过ACEWT方法得到希尔伯特包络谱,如图8所示。由图8可知,仍然提取出外圈故障频率及其倍频,但在故障频率32 Hz之前存在较高的低频噪声干扰。图7与图8相比,经过改进小波阈值函数去噪的信号,抑制了低频噪声,故障频率幅值提升一倍。因此,采用改进小波阈值函数预处理降噪,对轴承故障频率特征提取具有重要意义。

图8 ACEWT方法Fig.8 ACEWT method
2.3 方法对比
为了验证改进小波阈值函数-ACEWT方法对低信噪比轴承故障频率特征提取的有效性,分别采用EWT、改进小波阈值函数-EWT和MCKD-EWT三种方法进行故障特征提取对比,分别为图9、图10、图11所示。
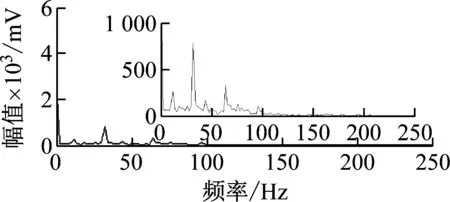
图9 EWT方法Fig.9 EWT method

图10 改进小波阈值函数-EWT方法Fig.10 Improved wavelet threshold function-EWT method
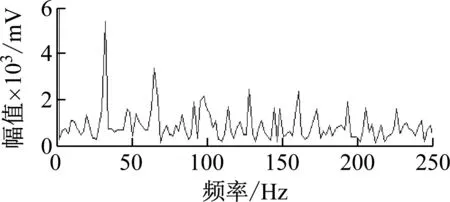
图11 MCKD-EWT方法Fig.11 MCKD-EWT method
图9为EWT方法处理图,图10为改进小波阈值函数-EWT方法处理图,图11为MCKD-EWT方法处理图(MCKD算法参数设置为L=200,M=2,T=32)。由图9~图11可知,EWT方法、改进小波阈值函数-EWT方法与MCKD-EWT方法对比,提取轴承故障频率特征微弱,说明应用的方法处理低信噪比信号,受噪声干扰大,故障冲击还未充分提取出来,轴承故障特征频率及倍频未有效提取。由图11可知,可准确得出轴承故障频率特征,但70 Hz以后的故障倍频特征未能提取。
通过以上的对比分析,本文所提出的改进小波阈值函数-ACEWT方法,对低信噪比信号可有效降噪,增强了故障冲击强度,并准确提取轴承故障频率32 Hz及其倍频。
3 试验验证
3.1 试验数据采集
为了进一步验证所提方法的有效性,将本文方法应用到滚动轴承故障诊断中,采用旋转机械试验平台和软岛全息声发射系统组成了滚动轴承声发射检测系统,试验平台见图12(a)。旋转机械平台包括①变频电机、②联轴器、③正常轴承、④平衡圆盘和⑤故障的轴承。试验过程中电机的转速保持为600 r/min,采样频率为3 MHz。待测试滚动轴承采用UN205EM型号,如图12(b)所示,外圈内圈可拆,并进行线切割来模拟轴承故障。内径为25 mm、外径为52 mm、节径为39 mm、滚动体数量为13个、滚珠体直径7.493 mm,外圈故障为0.1 mm宽凹槽。

(a) 旋转机械试验平台
滚动轴承外圈故障特征频率[23]计算公式为
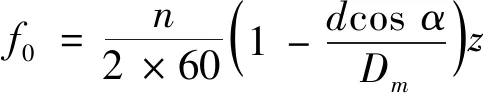
(18)
式中:n为轴转速;d为滚珠直径;α为接触角;Dm为轴承节径;z为滚动轴承滚珠个数。
由轴承参数与式(18)可计算本文实测轴承外圈故障特征频率为52.52 Hz,在下文数据处理中截取采样时间0.15 s对数据进行分析处理。
3.2 滚动轴承外圈故障分析
试验采集的滚动轴承外圈故障的声发射信号,并添加SNR=-20 dB的高斯白噪声来模拟现场环境,波形、频谱和包络谱如图13(a)、13(b)和13(c)所示。由图13(a)可知,滚动轴承的声发射信号已被噪声完全覆盖,最大幅值3.8 mv,由图13(b)、13(c)可知,轴承故障声发射信号的故障频率特征已提取不出。因此需要对声发射信号作进一步处理。
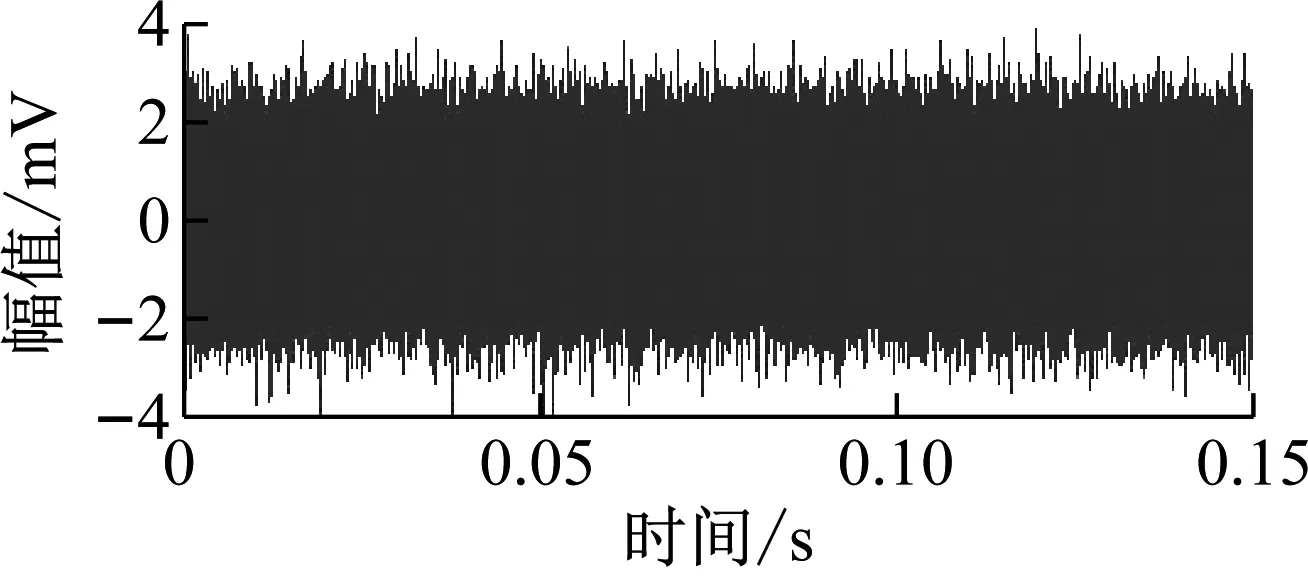
(a) 时域图
采用改进小波阈值函数降噪。同样采用Db8小波基函数对轴承故障的声发射信号进行小波分解,由于频率主要集中在50~100 kHz范围之内,因此分解为4层小波系数。其中调节因子的选取引用文献[24]中信号与噪声能量分布特征模型如式(19),进而确定调节因子u
(19)
式中:Enj为小波分解第j层噪声能量;Edj为小波分解第j层含噪信号能量;当j=1时,En1≈Ed1。由此得到每层U值,让每层U值归一化后确定每层调节因子u值。降噪后的波形如图14所示。由图14可知,轴承故障的弹性波冲击较明显。
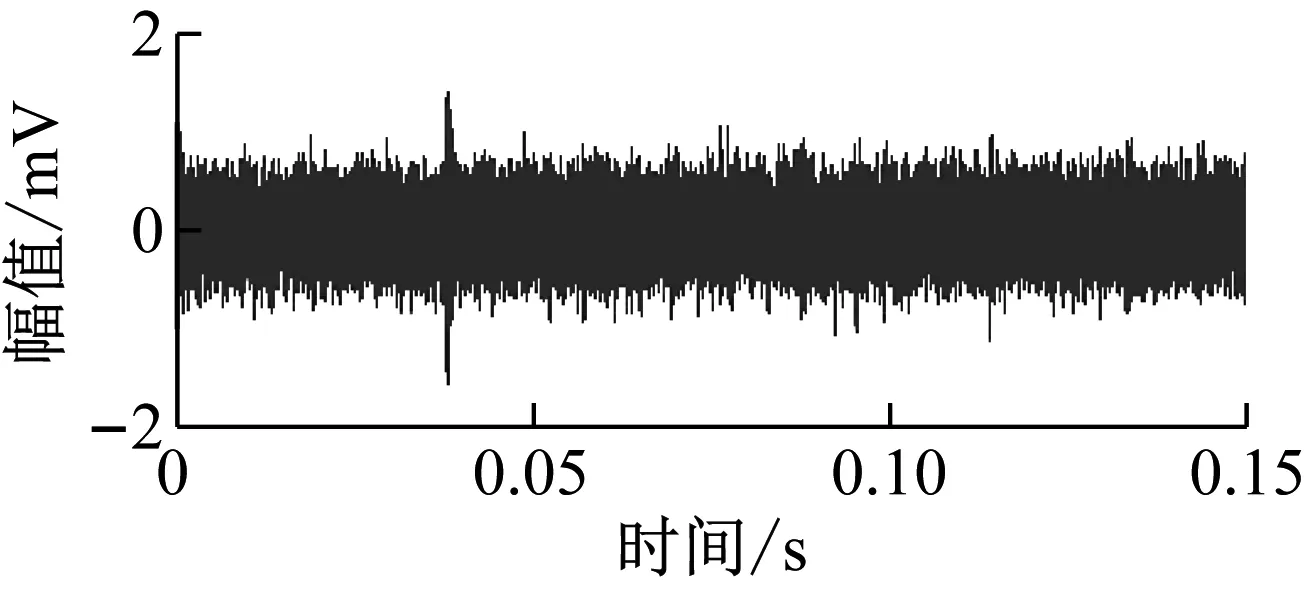
图14 滚动轴承故障降噪后波形Fig.14 Waveform of rolling bearing fault after noise reduction
分别采用EWT、改进小波阈值函数-EWT、MCKD-EWT和本文方法四种方法进行故障特征提取进行对比,如图15所示。在EWT方法分解中,设置分量数目为8,分解后都得到一层近似系数分量和七层细节系数分量,对七层细节系数分量采用经验小波能量比-熵指标进行筛选,选择大于经验小波能量比-熵指标平均值的细节系数分量,选取分量重构并进行希尔伯特包络谱分析。
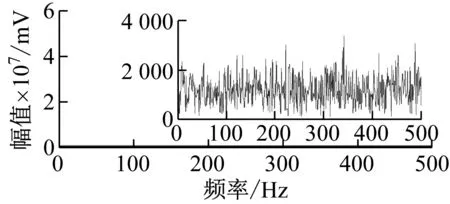
(a) EWT方法
图15(a)为EWT方法处理结果。滚动轴承故障的声发射信号直接进行EWT方法分析,从图15(a)中的 局部放大图可知,虽然提取了轴承外圈故障的故障频率及其倍频,但受噪声干扰,故障频率与噪声混淆在一起,这是因为EWT方法对低信噪比声发射信号分解时,会受噪声极大值的干扰,分解效果不理想,不能快速的识别故障频率,因此需对低信噪比声发射信号进行降噪预处理。
图15(b)为改进小波阈值函数-EWT方法处理结果;图15(c)为MCKD-EWT方法处理结果,MCKD算法参数设置为L=300,M=2,T=52。由图15(b)中的局部放大图可知,改进小波阈值函数根据声发射信号的冲击性与快速衰减的特点,对声发射信号进行预处理,结合EWT方法得到外圈故障频率及其1倍频、2倍频并较好地提取出来,改进小波阈值函数可对声发射信号有效降噪,但200 Hz以后的倍频未准确提取。从图15(c)中的局部放大图可知,采用MCKD方法进行预处理,可对外圈故障的周期冲击成分进行检测,从频率特征来看,200 Hz以后故障倍频很模糊。这说明在低信噪比下,外圈故障声发射信号周期还未充分的提取出来。
为了使外圈故障产生的周期性弹性波充分的提取出来,达到效果更好。采用本文提出的改进小波阈值-ACEWT方法进行分析。从15(d)中可知,能够准确提取轴承外圈故障声发射信号的故障频率及其倍频,即外圈故障频率为52.5 Hz。
相比于EWT、改进小波阈值函数-EWT、MCKD-EWT方法,本文方法明显优于EWT、改进小波阈值函数-EWT、MCKD-EWT方法,可对低信噪比声发射信号有效降噪、突出轴承故障的弹性波冲击,并能准确提取滚动轴承外圈故障声发射信号频率特征。本文提出的改进小波阈值函数-ACEWT方法为低信噪比声发射信号提取轴承故障特征提供一种新方法。
4 结 论
(1) 针对声发射信号具有冲击性与衰减的特点,提出了改进小波阈值函数降噪法(即衰减正弦型与指数型的小波阈值函数)。通过仿真信号分析,弥补了软、硬阈值函数的缺点,避免了一部分有用信号的丢失,通过信噪比、均方根误差指标相比于其他阈值函数有更好效果,且在低信噪比中更加适用。
(2) 针对低信噪比情况下,轴承故障频率特征难提取问题,提出了改进小波阈值函数-ACEWT方法。将该方法与EWT、改进小波阈值函数-EWT、MCKD-EWT对比研究,并应用到滚动轴承故障声发射信号诊断中。仿真与试验结果表明,改进小波阈值函数-ACEWT方法能对低信噪比声发射信号有效降噪、突出信号中周期性弹性波特征,实现了滚动轴承故障声发射信号频率特征准确提取,验证了该方法的有效性。
