多频激励作用下悬索时滞减振控制研究
2023-09-20李禄欣孙洪鑫禹见达邵宏利
夏 慧,彭 剑,2,李禄欣,孙洪鑫,2,禹见达,2,邵宏利
(1.湖南科技大学 土木工程学院,湖南 湘潭 411201;2.湖南科技大学 结构抗风与振动控制湖南省重点实验室,湖南 湘潭 411201)
悬索作为大跨度空间结构的一种重要形式,被广泛应用于建筑工程(体育馆),桥梁工程(悬索桥),电力电讯工程(输电线),航空航天(绳系卫星)等领域。在实际工程中,悬索受到的外部荷载较为复杂,可能存在多个激励共同作用,作为非线性系统,在多频激励作用下会表现出更为复杂的动力学行为[1]。研究人员针对Duffing[2-3]、Vander Pol[4]、Duffing-van der Pol[5-6]等经典系统在多频激励作用下的非线性动力学行为进行了研究,发现多频外激励改变了单频激励条件下系统的振动状态,使系统的主共振曲线产生了偏移。赵珧冰等[7]基于温度变化对拉索张拉力和垂度的影响,研究了悬索联合共振的响应特性及其受温度变化影响。孙测世等[8]针对分布与端部激励下悬索瞬时相频特性开展了对比研究。
另一方面,悬索因其本身质量轻,柔性大,阻尼小等特点,在多频激励的作用下容易产生大幅度的振动[9-11],造成结构的疲劳破坏,从而导致工程灾害的发生。因此悬索的振动控制问题一直备受研究者关注[12-14]。从Olgac等[15-16]提出动力结构主动时滞减振新技术,研究人员对时滞反馈控制进行了大量的研究。赵艳影等[17]研究了时滞非线性动力吸振器的减振机理。王在华等[18]对相关时滞动力系统的稳定性和分叉内容进行了系统阐述。邵素娟等[19]研究了具有时滞反馈控制的非线性主动悬架系统的稳定性。彭剑等[20]采用时滞反馈控制对悬索在单一激励作用下动力学行为进行了研究。
综上所述,悬索作为一类典型的运动方程同时包含平方和立方非线性的柔性结构,当其受到多频激励时,容易发生各种形式的联合共振,然而现有研究较少。因此,本文关注多频激励作用下悬索的时滞反馈控制问题。基于Hamilton变分原理,建立多频激励下受控悬索系统的非线性振动控制模型。利用多尺度法求解受控悬索系统发生联合共振时的响应方程。通过数值算例分析了受控悬索的非线性行为,以及控制系统参数对共振响应的影响。
1 数学模型
如图1所示,建立坐标系O-xy,悬索的两端悬挂在O-xy坐标面内的同一水平线的两个支座上,坐标原点O位于悬索的一侧,同时用虚线和实线分别表示悬索的静态和动态构型。u(x,t)和v(x,t)分别表示沿x和y方向的位移分量。假设沿悬索索长方向的截面积保持不变,悬索始终保持在弹性变形范围内,同时忽略弯曲刚度、扭转刚度以及剪切刚度的影响。

图1 受控悬索系统的简化模型Fig.1 Simplified model of a controlled suspended cable system
基于Hamilton变分原理,可以得到多频激励下受控悬索系统的非线性动力学方程[20]
(1)
式中:点为对时间t求导,撇为对坐标x求导;l为悬索的跨径;m为悬索单位长度的质量;E为悬索的弹性模量;A为悬索横截面面积;H为悬索初始张力的水平分量;c为单位长度的阻尼系数;uc为右端移动支承的纵向位移。为了便于参数分析,假定悬索的初始静态构型为抛物线[21]:y(x)=4b[x/l-(x/l)2],其中b为悬索的垂度。外部激励由两部分组成(m=1,2),Kmn、Ωm和θm分别为激励的幅值,频率和相位。g为重力加速度,引入无量纲参数

(2)
经过无量纲化,方程(1)转化为以下形式
(3)
为了书写方便,字母的上标已略去。
假设悬索是由正对称和反对称模态组成的多自由度系统,可利用Galerkin法将式(3)离散成无穷维方程,此时面内运动的位移函数表示为
(4)
式中:qn(t)为广义坐标函数;φn(x)为振型函数。
将式(4)代入式(3)中,可得离散后的无穷维方程为
(5)
其中,

(6)
2 超/亚谐波联合共振
由于悬索同时包含平方和立方非线性,非线性共振现象丰富,如主共振;1/2、1/3阶次谐波共振;2阶、3阶超谐波共振等。当其受到多频激励时,会发生多种形式的联合共振或组合共振,本文考虑系统同时发生超谐波共振和亚谐波共振,利用多尺度法求解系统的幅频响应方程,并且判断稳态解的稳定性。
根据多尺度法,调整阻尼项,非线性项及外激励项的系数,即μn=O(ε2),Λnijk=O(ε2),gl=O(ε2),Γnij=O(ε),设式(5)解的形式如下:
qn(t;ε)=qn0(T0,T1,T2)+εqn1(T0,T1,T2)+
ε2qn2(T0,T1,T2)+O(ε2)
(7)
其中,Ti=εit,(i=0,1,2),ε(0<ε≤1)为小参数。
将式(7)代入式(5),并令两端εi的系数相等,得到:
(8)
(9)
glc1D0qn0(t-τ)-glc2qn0D0qn0(t-τ)
(10)
式(8)的解可表示为以下形式
(11)
其中,cc为前面各项的共轭复数以及
将式(11)代入式(9)中,消去久期项,可知D1An=0,由此可得qn1的表达式。将所得结果代入式(10)中,同理消去久期项可知qn2的表达式。
本文分析超谐波共振和亚谐波共振联合共振的情况,设:
3Ω1=ω1+ε2σ1,Ω2=3ω1+ε2σ2
(12)
其中,σ1和σ2为调谐参数。则式(10)的可解性条件为
iglc1Ane-iωnτ=0
(13)
式中:δn1为克罗内克δ函数;上标横线表示共轭项。其他参数如下
pm=
smk=
(14)
令:
(15)
其中,an和βn为T2的实函数。
在实际工程中,悬索的前两阶模态(一阶正/反对称模态)较易激发,也更易测试。因此,为简便起见,本文考虑单模态模型(一阶正/反对称模态)[22]。将式(15)代入式(13),分离实虚部,当n=1时,可得:
(16a)
(16b)
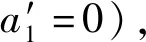
(17)
即σ2=3σ1=3σ时才存在稳态运动,此时Ω2=9Ω1。可得稳态运动方程:
μea1-2p1sin(γ+3θ1)-
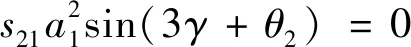
(18a)

(18b)
其中,
(19)
3 算例分析
本节对多频激励下受控悬索联合共振响应开展数值分析。悬索的各项物理参数分别为[23]:跨度L=200 m,截面面积A=7.069×10-2m2,弹性模量E=200 GPa,密度ρ=7 800 kg/m3,阻尼比μn=0.005。悬索的非线性振动特性与其垂跨比的大小相关,本文取垂跨比为适中值0.015。
令方程组(18)中的θ1=θ2=0,可以得到悬索在超谐波与亚谐波联合共振情况下的幅频响应曲线和对应的调谐相位曲线,如图2~图6所示。实线和虚线分别表示稳定解和不稳定解。幅频响应曲线都向左弯曲,表现出软弹簧特性。在多频激励作用下系统同时展现出超谐波共振和亚谐波共振响应的特性,但又与单一的超谐波和亚谐波共振特性不同,其共振区间、响应幅值及其相位等均发生了改变。其中,A和D两枝类似于悬索发生超谐波共振响应时的幅频响应曲线,B和C两枝类似于悬索发生亚谐波共振响应时的幅频响应曲线。在多频激励作用下系统的稳态解个数也发生改变,其解存在以下可能性:一个稳定的非平凡解;三个非平凡解,其中一个是不稳定的;五个非平凡解,其中两个是不稳定的;七个非平凡解,其中三个是不稳定的。
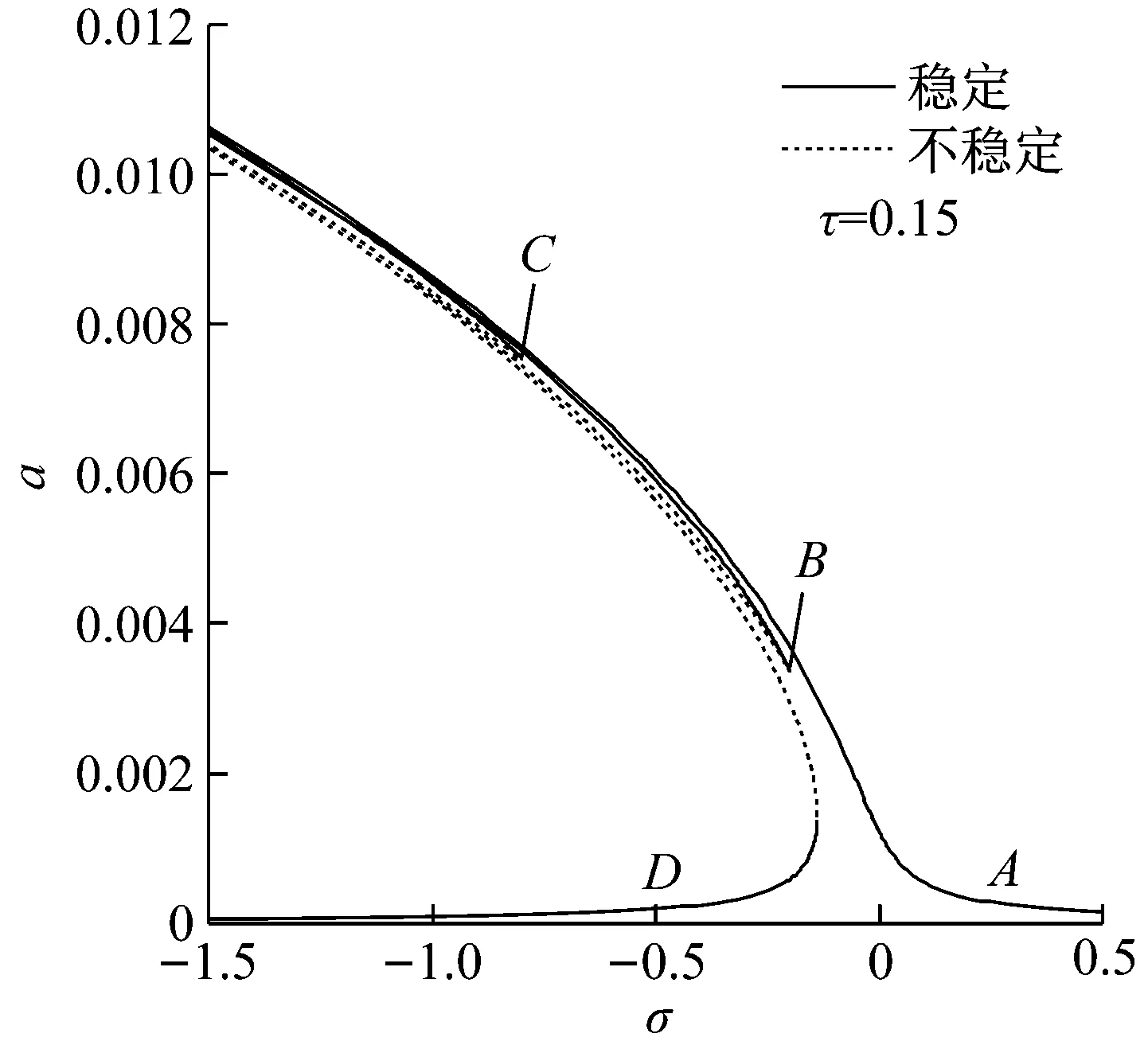
(a) 幅频响应曲线
由图2可知,当gl=0.000 1,τ=0.15时,σ取不同值,分枝B和分枝C可能彼此相交,也可能不相交,而当σ值适当大时,所有分枝皆不相交,即曲线不闭合。随着控制增益的增大,如图3所示,在gl=0.000 2,τ=0.15时,分枝B向下移动并形成一个循环,环的下部是稳定的,而上部是不稳定的。进一步提高控制增益,如图4所示,在gl=0.000 3,τ=0.15时,悬索仍表现出一定的软弹簧特性,但在频率响应曲线上存在一定的间隙,超谐波共振型曲线分成两条,特别地,分支A是封闭的并且大部分是单值的,只有小范围内存在多值。由图2~图4可以看到,给定时滞τ=0.15时,随着控制增益减小,分枝D的稳定和不稳定解的相位变得相当接近。此外,由图2、图5、图6可以发现,当gl=0.000 1时,时滞值从τ=0.15增大到τ=0.25,分枝B上移,分枝C下移,两个分枝之间的距离逐渐减小。

(a) 幅频响应曲线
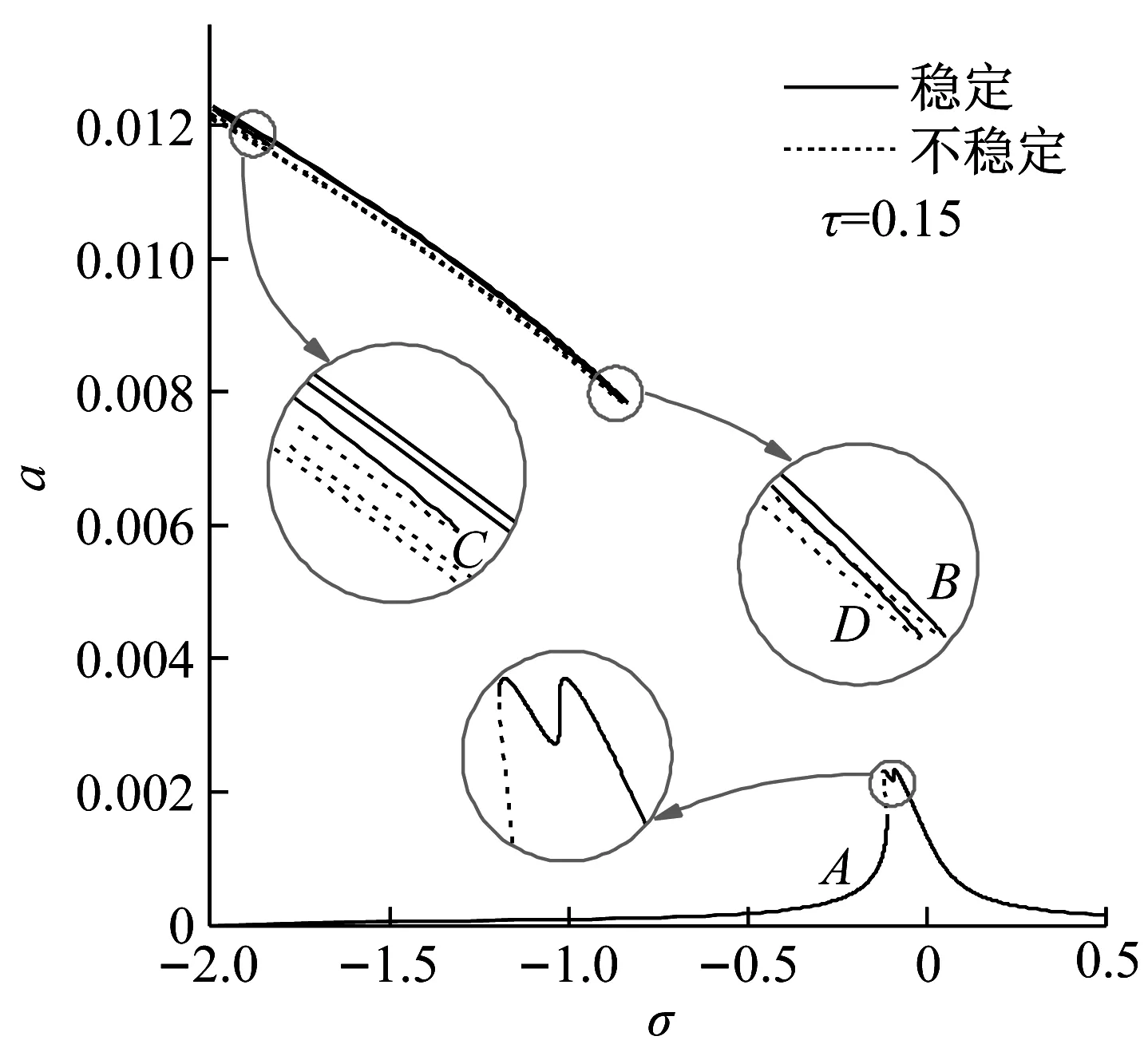
(a) 幅频响应曲线

(a) 幅频响应曲线
综上所述,通过调节控制增益和时滞值的大小可以改变共振范围、响应幅值及其相位。且控制增益和时滞值对相位的影响较大。当多频激励下的振动行为较为复杂时,可以通过频率响应曲线和调谐相位曲线来区分所有解。
4 结 论
本文主要通过多尺度法和具体的算例研究了多频激励作用下受控悬索的非线性振动特性,可以得到以下结论:
(1) 受控悬索表现出软弹簧特性,在多频激励作用下表现出复杂的非线性,超谐波和亚谐波联合共振作用下最多可以达到七个解。分枝B和分枝C之间的距离随着时滞值增大而慢慢变小,同时可以发现,随着控制增益减小,分枝D的稳定和不稳定解的相位变得相当接近。
(2) 通过调节控制增益和时滞值的大小可以改变悬索的共振范围、响应幅值及其相位。当多频激励下的振动行为较为复杂时,可以通过频率响应曲线和调谐相位曲线来区分所有解。
