基于参考信号重建的双层隔振系统主动控制试验研究

章 锐,韩志远,王朝政,张 磊,沈 星

(1.南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016;2.北京航天长征飞行器研究所,北京 100076)

振动控制可以分为被动控制与主动控制,舰船被动控制按照发展历程分为:单层隔振系统、双层隔振系统、浮筏隔振系统。相对于单层隔振系统,双层隔振传递率可以实现更快速度的衰减,同时双层隔振具有结构较简单、易于实现、经济性及可靠性好、不需要外界能源等优点,被广泛的应用于航空、航天、舰船、车辆等领域。双层隔振系统以更低的传递率能显著降低机械设备的振动向外界传递,是结构噪声和振动隔离的有效控制措施。然而,传统的被动隔振由于机械设备高静态刚度设计要求与结构低动刚度要求之间的矛盾,导致低频振动控制一直是被动隔振的瓶颈[1-3]。

主动振动控制的思想理念与主动噪声控制相似,主动噪声控制[4]是在误差信号麦克风附近产生相反的信号与噪声相互抵消来降低噪声,主动振动控制[5]的原理是通过调节主动控制力的大小和相位,使其产生的振动响应与振源产生的振动响应相互抵消,减小振动向外部结构的传递。因此主动控制技术不仅能有效控制机械设备低频振动的传递,而且还能适应振源频率的变化与不同的被控对象,具有广阔的应用前景。

自适应前馈控制算法FXLMS在主动控制领域得到了广泛的应用。YANG等[6-8]采用MIMO FXLMS算法来抑制柴油发动机在双层隔振系统中运转时产生的振动,试验表明该算法能实现多点主频和多数倍频下的加速度振级衰减。Seba等[9]针对汽车发动机的低频振动问题,采用FXLMS算法与H∞控制方法进行试验对比研究,得出FXLMS算法具有更好的控制效果,H∞算法控制更稳定的结论。Kauba等[10]针对潜艇动力机械的振动问题,采用多通道FXLMS算法在舰船上对整套主动控制系统进行了实船测试。Owens等[11]采用重复控制方法解决了六自由度Stewart平台上的周期性扰动问题,取得了约50 dB的减振效果。Niu等[12-13]采用变步长bang-bang的在线建模FXLMS算法控制垂直尾翼的振动,有效降低了结构在随机激励下的振动响应。Snyder等[14]探究了传递函数的建模误差对FXLMS算法噪声主动控制的影响。然而,使用FXLMS算法的前提是认为扰动信号是周期稳定的信号[15],在实际应用中,舰船、汽车等动力械器设备工作时的转速是不断变化的,主频在一定范围内波动,参考信号不再稳定,经典FXLMS算法会出现控制不稳定的问题[16]。

本文以双层隔振系统为研究对象,采用经典FXLMS算法对电机不同转速下进行控制试验;针对电机振动信号频率的波动与参考信号受控制信号影响等问题,设计了一种基于反馈理论的参考信号重建FXNLMS算法,通过仿真分析验证了该算法的有效性。搭建试验平台,采用NLMS算法获取误差通道的数学模型,并在多工况条件下与经典FXLMS算法进行试验对比,试验结果表明参考信号重建算法具有更好的稳定性和抗干扰能力。本文的研究内容填补了国内舰船双层隔振领域的空白。

1 双层隔振主动控制试验平台

1.1 试验平台

根据舰船柴油发电机组双层隔振系统的结构形式,本文搭建了双层隔振试验平台如图1所示,试验平台采用激振力25 kgf的振动电机作为振源,转速范围为0～3 600 r/min;电磁式作动器安装在中间层,层与层之间采用4个BE型橡胶隔振器相连,整体结构与光学试验平台刚性连接,橡胶隔振器与刚性连接件以主惯性轴对称分布。加速度传感器布置在上层板与弹性钢板上,其中误差传感器布置于橡胶隔振器旁,位于主要模态的大变形处,可以通过测量弹性钢板上传感器位置处的振动情况来评价主动控制系统的减振性能[17]。

图1 控制试验平台Fig.1 Control test platform

1.2 主动控制系统

图2为控制系统硬件示意图,整个控制系统由加速度传感器、滤波器、cRIO控制器、模拟量输入输出模块、功率放大器与电磁式作动器组成。未开启控制前,先由安装在弹性钢板上的加速度传感器2测量并记录振动响应,以了解被动隔振的效果。FXLMS算法开启后,加速度传感器1测量上层板的振动信号作为控制系统的参考输入信号,控制器同时获得误差位置处2的振动信号作为反馈,经过控制算法计算出作动器的输出,作动器在弹性钢板上产生与电机传递振动反向的振动响应,从而降低弹性钢板上的振动。滤波器设置的截止频率为100 Hz,作为控制过程中的最大频率。同时试验平台通过刚性连接件与光学试验平台相连,以减少来自底部的外部干扰。

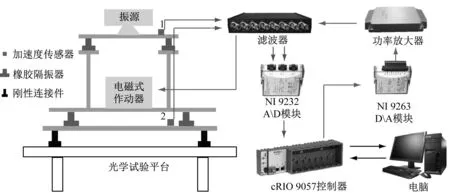
图2 控制系统硬件示意图Fig.2 Hardware diagram of control system

1.3 FXLMS自适应滤波算法

FXLMS是一种常见的自适应滤波算法,该算法是LMS算法的改进版,它利用梯度下降算法更新产生控制输出的FIR滤波器的参数。该算法考虑了从控制执行器到误差传感器的路径,以避免控制通道的引入造成的不稳定性问题。FXLMS算法由于其鲁棒性和快速收敛特性,在主动噪声控制与振动主动控制领域被广泛研究[18]。

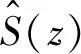
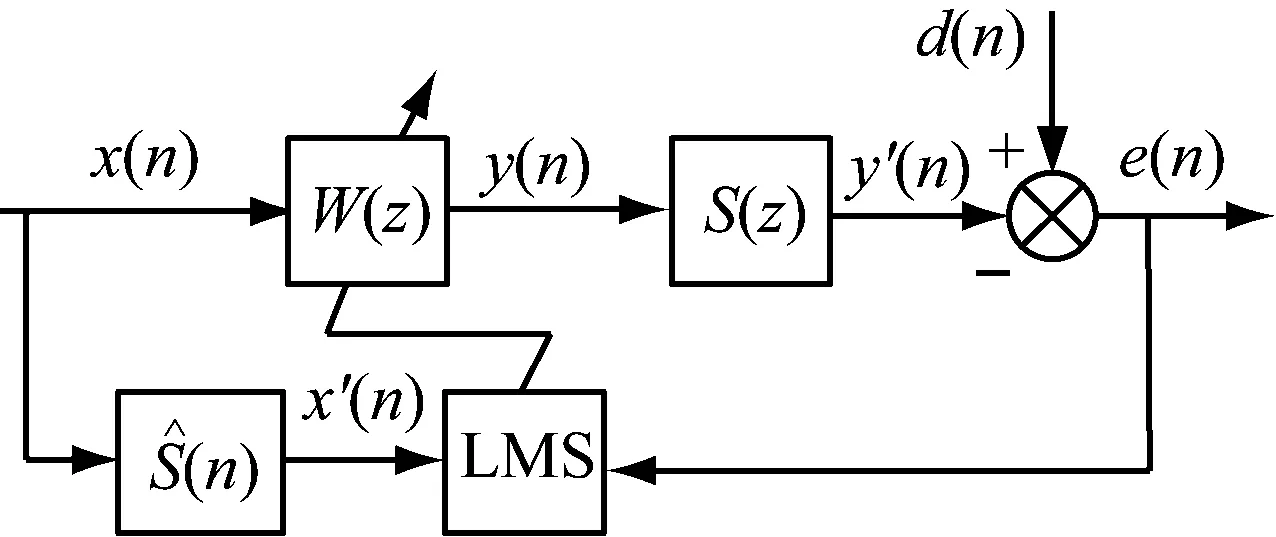
图3 FXLMS控制系统框图Fig.3 Block diagram of FXLMS control system

1.4 误差通道离线建模

误差通道也称为次级通道,指控制器输出到误差信号之间的传递路径,包括D/A转换器、带通滤波器、功率放大器、电磁式作动器、从作动器位置到误差传感器位置的物理系统、传感器自身、低通滤波器和A/D转换器。误差通道的振动特性体现了控制系统输出到误差信号之间的幅频增益和相位延迟,在控制系统设计时必须加以考虑和补偿,否则会影响控制系统稳定和性能[19]。本文采用的误差通道辨识方法为自适应N-LMS滤波算法[20],该算法原理与LMS算法一致,主要区别为该算法考虑了噪声信号对辨识过程稳定性的影响,其控制算法可以简单的描述为

(1)

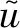
误差通道权向量时序图如图4 (a)所示,其中虚线由采集的输入输出数据在Matlab拟合得到,实线由编写的实时控制程序计算得出。如图4 (b)为期望信号与误差信号随时间的加速度幅值变化图。由图可知,误差通道权向量仿真数据与试验数据具有很高的重叠度,误差信号到达稳定状态的误差范围总体上控制在5%以内,共同说明误差通道建模的准确性,可用于后续主动控制试验。

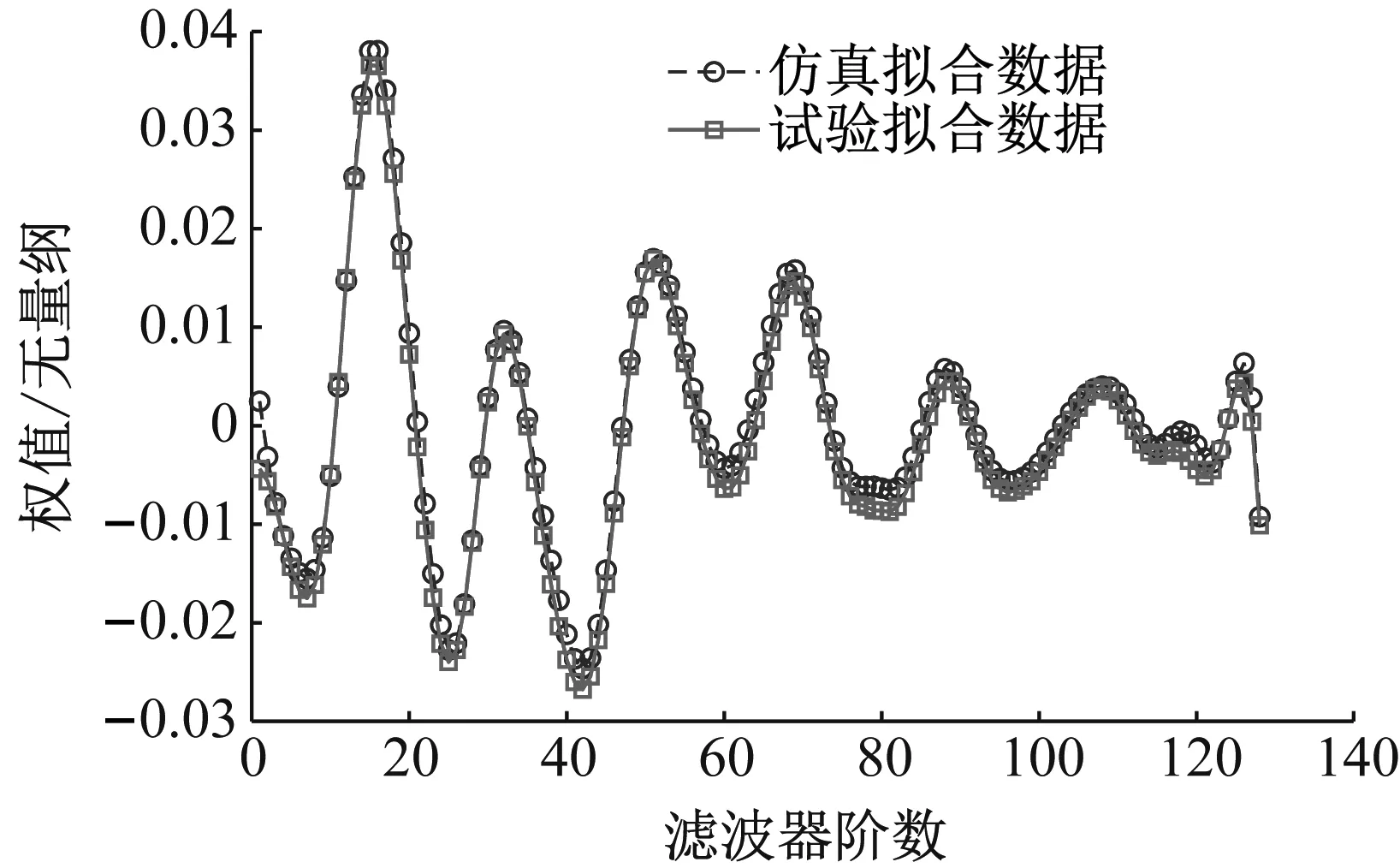
(a) 误差通道模型

2 基于反馈理论的参考信号重建

2.1 信号重建理论

在主动控制系统中,FXLMS算法的参考信号来自上层板加速度传感器1的振动响应,振动电机不同工作状态对应特定的响应输出。但在实际控制过程中,作动器的输出会对参考信号产生不同程度的影响,同时电机的转速在一定频率范围内波动,这将导致误差位置处的控制达不到理想的效果。

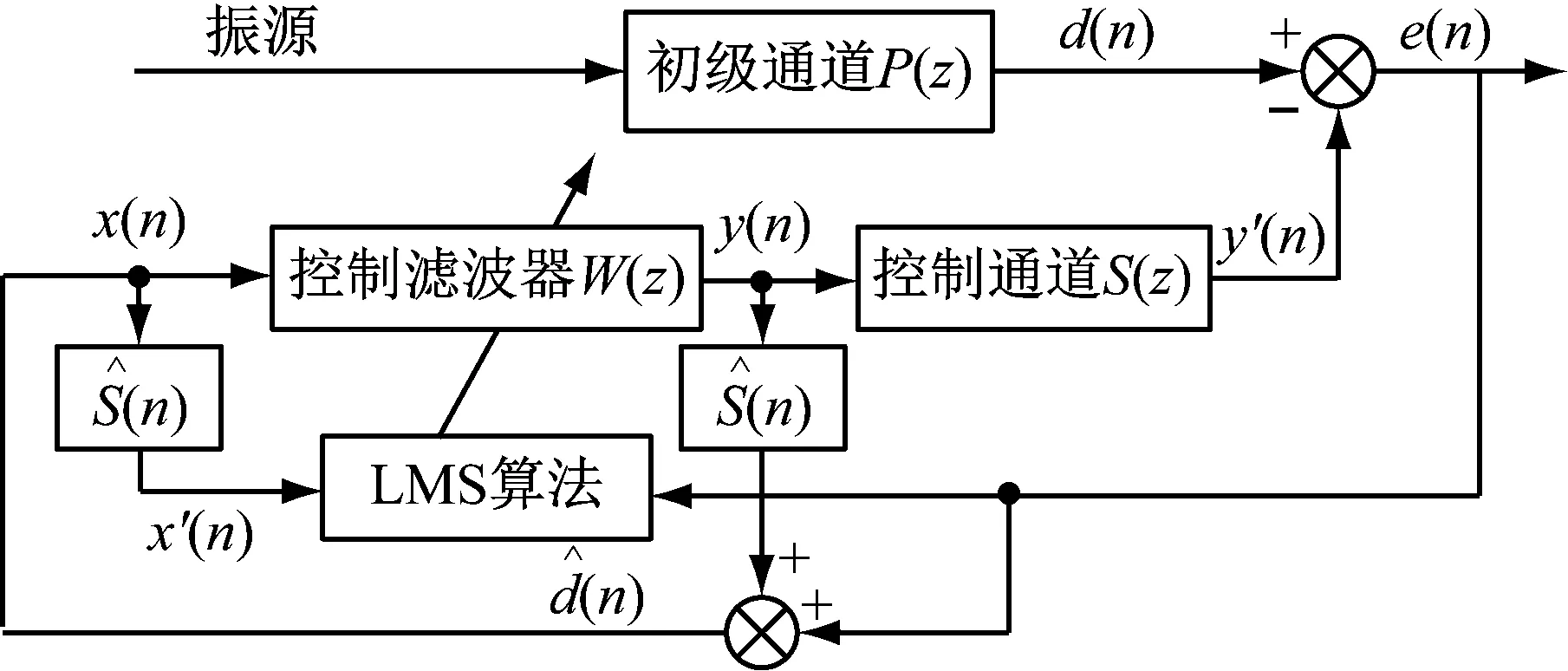
图5 参考信号重建算法框图Fig.5 Block diagram of the reference signal reconstruction algorithm

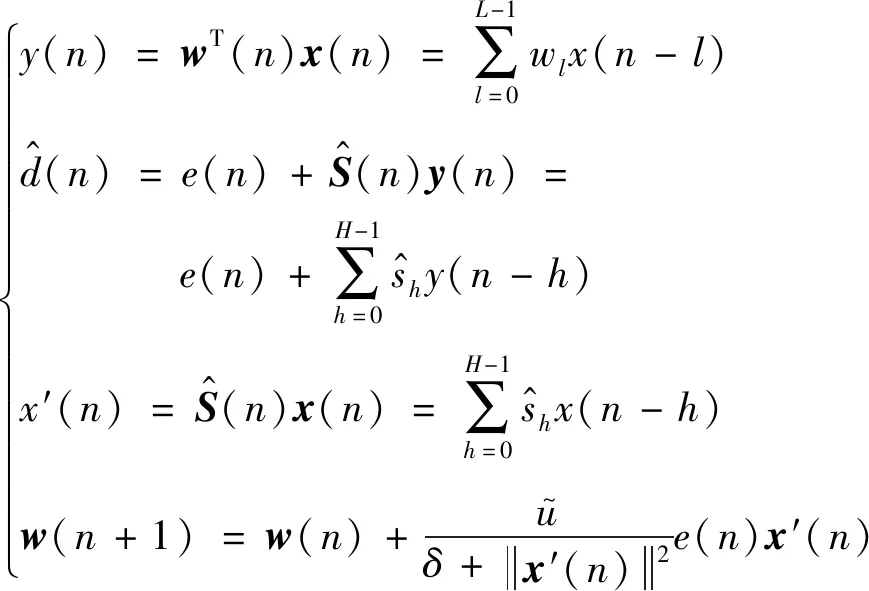
(2)

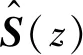
x′(n)=[x′(n)x′(n-1)…x′(n-N+1)]T

(3)

w(n+1)=[w0(n)w1(n) …wN-1(n)]T

(4)

(5)

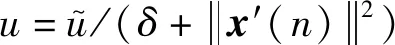
与FXLMS算法对比,参考信号重建的FXNLMS算法不需要加速度传感器采集参考信号,节省了硬件成本。

2.2 仿真分析

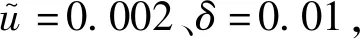
图6和图7为单频与多频条件下控制信号时域与频域图。从图中可以看出,单频与多频条件下误差信号收敛速度快、稳态误差小,重建的参考信号与实际参考信号具有很高的重合度,表明了参考信号重建算法的有效性与稳定性。25 Hz与40 Hz单频工作频率下,控制前后加速度振级衰减分别可以达到63 dB、112 dB;多频工作频率下,主要频率处控制前后加速度振级衰减分别达到19 dB、74 dB。稳定后的误差信号主要保留了输入信号中的宽频噪声,说明该算法受干扰信号的影响较小。

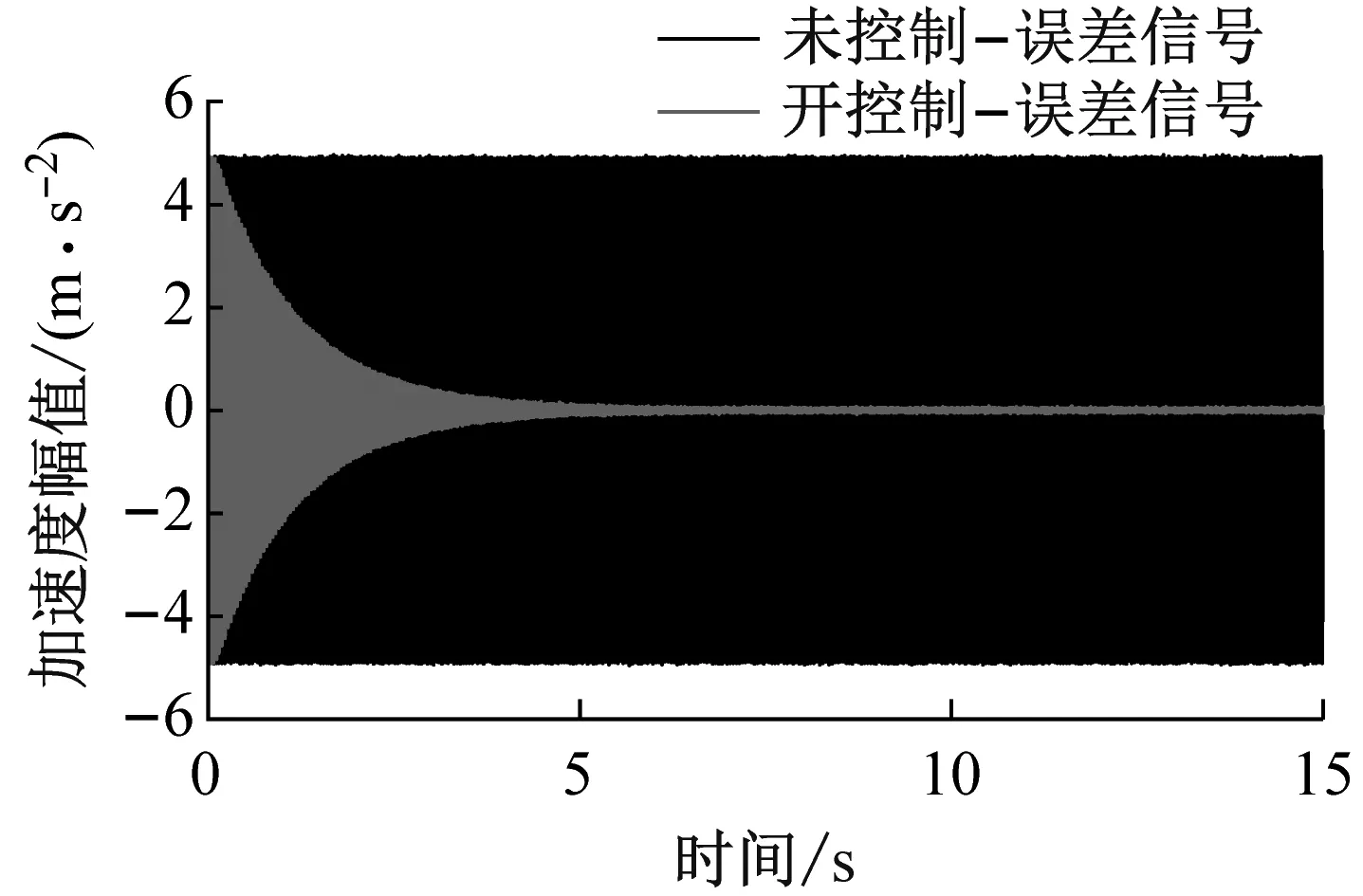
(a) 25 Hz误差信号

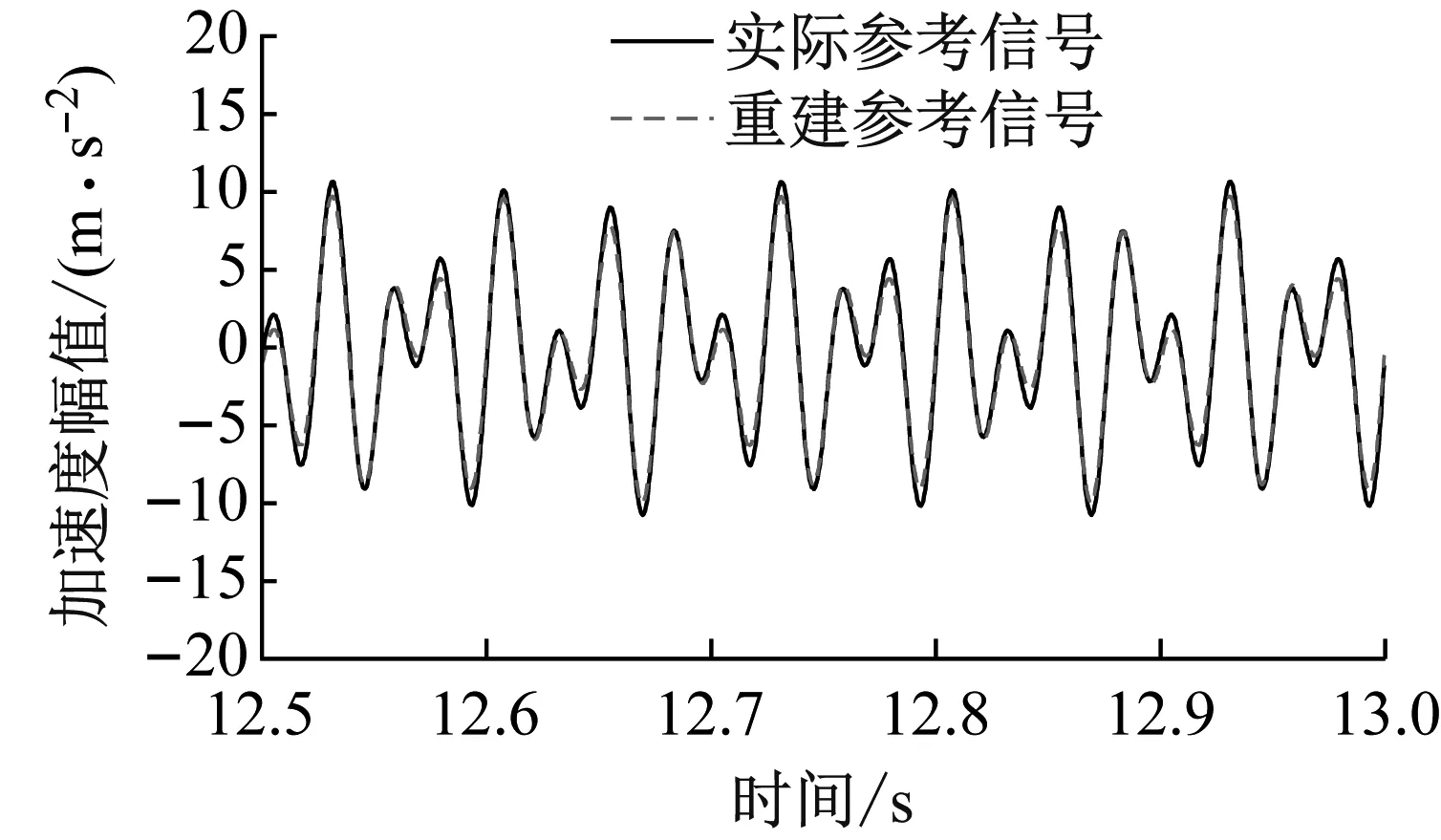
(a) 双频参考信号

3 双层隔振系统试验验证

双层隔振主动控制系统的试验平台与硬件原理见图1和图2。当参考信号重建算法实施主动控制时,加速度传感器2采集弹性钢板处的振动信号作为控制器的输入,控制器输出信号与次级通道权向量进行卷积,与误差信号的线性叠加作为控制算法的参考信号并不断更新输出信号的值,经过调理放大后作用于电磁式作动器,实现对被控对象的振动抑制。控制器硬件由cRIO-9057、输入模块9232和输出模块9263构成,控制软件用LabVIEW语言编制。通过调节振动电机的转速完成不同工况下的振动主动控制试验。

图8为振动电机在25 Hz到40 Hz运转下误差信号控制前后的时域与频域图,表1是电机25 Hz到40 Hz以2.5 Hz为间隔依次运转,误差信号在电机主频处的控制效果。

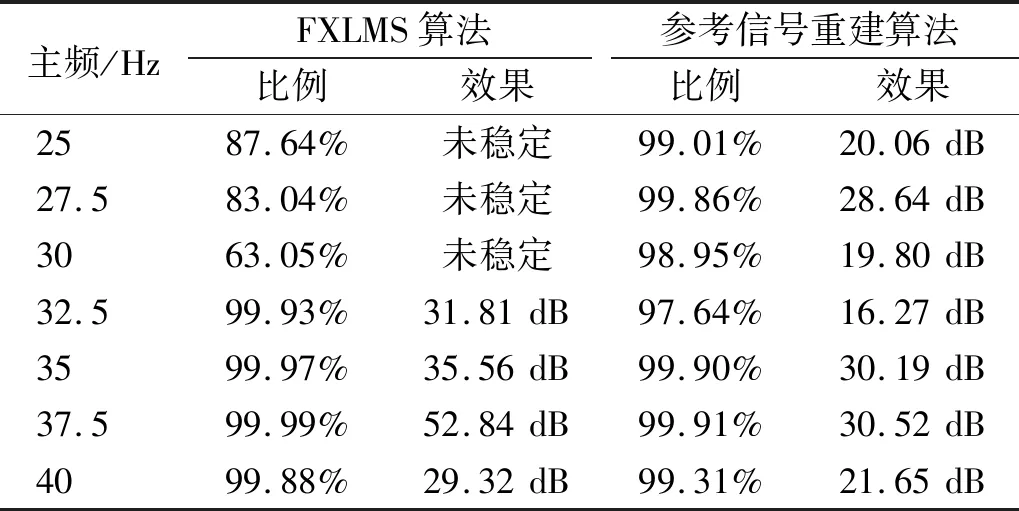
表1 不同频率下试验减振效果Tab.1 Test vibration damping effect at different frequencies

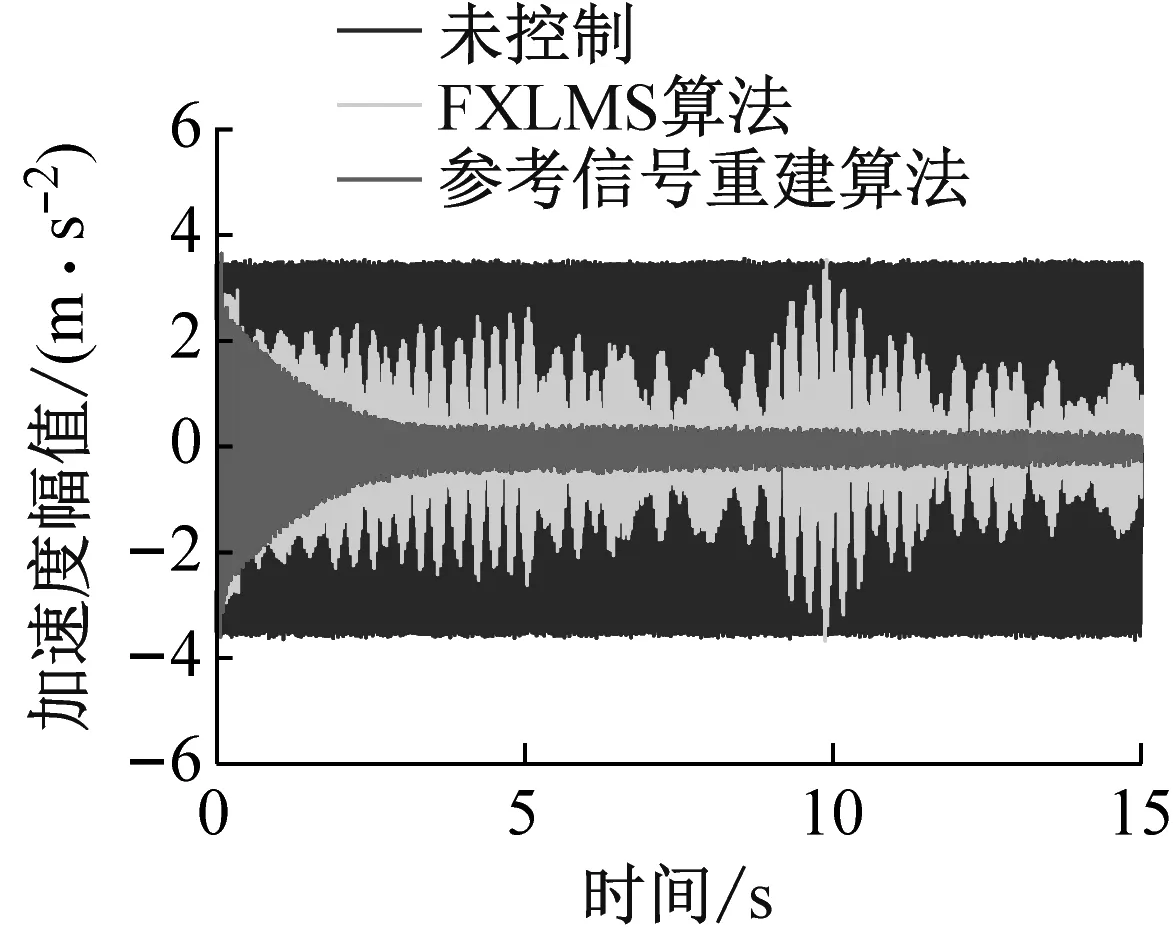
(a) 25 Hz误差信号

由图8与表1可以看出:

(1) 电机25 Hz运转情况下,FXLMS算法在主频处可以实现9.08 dB控制效果,但同时引入了宽频输出信号,导致系统一直处于震荡不稳定状态;在电机在27.5 Hz与30 Hz运转情况下,FXLMS算法同样不能使系统达到稳定的输出状态;

(2) 电机40 Hz运转情况下,FXLMS算法在主频处可以实现29.32 dB的控制效果,控制过程中误差信号出现小幅震荡,随时间震荡减小并逐渐消失,系统最终达到稳定状态;在电机32.5 Hz至37.5 Hz运转情况下,FXLMS算法均可以实现主频处加速度振级衰减99%以上;

(3) 在电机32.5 Hz和35 Hz运转情况下,控制系统稳定后,FXLMS算法误差信号出现小幅扰动,而参考信号重建算法信号较为稳定,说明重建算法较FXLMS算法具有更高的抗干扰能力。

(4) 电机25 Hz到40 Hz运转情况下,参考信号重建算法均可实现主频处加速度振级衰减97%以上,有效解决了FXLMS算法在部分频率处控制不稳定的问题。

4 结 论

本文搭建了双层隔振系统主动控制试验平台,采用最小均方算法建立了误差通道模型,通过仿真与试验验证了通道模型的准确性,为通道在线建模提供了试验基础。针对参考信号受作动器输出信号的影响导致系统不稳定的特点,设计了一种基于反馈理论的参考信号重建算法,通过仿真分析验证了该算法在单频与多频条件下的稳定性;仿真分析结果表明,该算法具有信号重建能力强、信号收敛速度快、稳态误差小等优点。最后通过试验比较了FXLMS算法与参考信号重建算法的控制效果,结果表明FXLMS算法只能在部分条件下具有控制效果,参考信号重建算法在多种控制条件下均能达到95%以上的加速度振级衰减,控制效果整体上优于FXLMS算法,同时节省了硬件成本。

收敛速度是评价振动控控制效果的重要指标,单一参数的归一化步长因子难以满足多工况条件下对收敛速度的要求,在本文的基础上可进一步开展归一化变步长和自适应变步长等研究工作。