某型号卫星控制力矩陀螺隔振装置设计和试验技术研究

孙晓晨,郭 彤,李晓莉,姚小松,杨若宸

(中国科学院微小卫星创新研究院,上海 201304)

由于遥感卫星在高精度、全球观测,及近似实时快速地获取空间信息方面的出色表现,遥感卫星已经承担了气象预报、侦察测绘等与日常生活紧密相关的任务,因此遥感卫星的精度需求也日益提高。而提高卫星分辨率的有效手段之一就是:为遥感器提供超静、超稳的工作环境,这种方式具有成本低、研制周期短、效果明显的特点,可以直接抑制卫星平台在轨微振动,从而保证敏感光学载荷在轨成像能力。

为降低微振动环境对敏感载荷性能的影响,通常采取被动隔振措施将CMG、飞轮等扰动源与卫星平台隔离。美国哈勃望远镜对动量轮进行了振源隔离,空间望远镜也采用了阻尼层抑制微振动[1],国内风云四号卫星上也采用了隔振器对飞轮进行被动隔振[2],高分七号卫星上也在CMG和安装面之间设置了隔振装置[3],吉林一号高分星安装了金属橡胶隔振器隔离飞轮的影响[4]。

在某型号高分辨率遥感卫星上,采用我国某型控制力矩陀螺(control moment gyroscope,CMG)作为整星姿态控制设备。由于CMG在轨工作时高速转动(几千转),其转子转动产生的动、静不平衡力和不可避免的装配误差将会持续输出扰动,甚至激发卫星蜂窝板等结构振动,进一步传递至敏感载荷处,使光学载荷、星敏等载荷一直处于微振动环境,从而降低了遥感卫星的精度和分辨率。本文针对该高分辨率遥感卫星的CMG引起的微振动扰动,分析隔振装置的功能需求,设计CMG微振动抑制系统,并建立隔振系统的数学模型和力学仿真模型,在此基础上,采用实物进行了单机级、整星级微振动试验,并获得了实验数据。

1 隔振装置优化设计方法

1.1 CMG扰振特性

星上采用的某型CMG具有控制力矩大、控制精度高、能量消耗低等特点[5],单件质量为17.9 kg,内转子恒定转速6 000 r/min条件下,标称角动量为25 Nms。其主要结构可分为外框和内框两部分,如图1所示,主体尺寸包络为。其中外框为固定部分,包含CMG结构框架及内部控制电路,内框为转动部分,可以使内部高速转子在内框里绕Z轴高速转动并且内框整体可以同时绕Y轴旋转。在轨状态下,内部高速转子工作转速为6 000 r/min,CMG通过改变高速转子旋转轴的指向与卫星交换角动量来控制卫星的姿态。内部高速转子、内框转动所引起的动、静不平衡力及装配误差会引起振动。除CMG工作转动频率(100 Hz)外,由于保持架运转还存在约0.6倍频的谐波频率,因此CMG振动特性的频率成分主要60 Hz、100 Hz及其倍频。

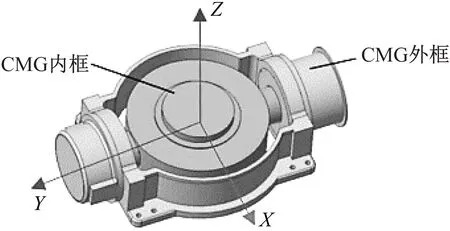
图1 某型号CMG结构示意图Fig.1 The structure of CMG

1.2 隔振系统的设计

因此可得到某型号卫星频率分布如图2所示。

图2 某型号卫星频率分布图Fig.2 The frequency of satellite

由于被动隔振方式性能稳定、可靠性高,因此采用被动隔振方式,具体将隔振装置安装在蜂窝板结构与CMG之间,主要用于抑制卫星在轨工作时CMG自身引起的扰振,使其对光学组件成像质量影响最小,同时也要满足卫星姿控要求,使CMG产生的控制力矩正常传递到卫星结构。

根据CMG的安装接口、结构特征以及功能需求,将四个完全相同的金属隔振器按照汇聚式结构并联,该结构具备承载能力高、结构刚度大、运行稳定、装配公差容许度高等优势,同时设计上转接框架为CMG和隔振器提供转接接口,下转接框架可以提供隔振子系统与卫星舱板的安装接口,子系统在整星的安装效果如图3所示。隔振系统包括CMG、上转接框架、金属隔振器、顶杆、下转接框架、热刀解锁装置。

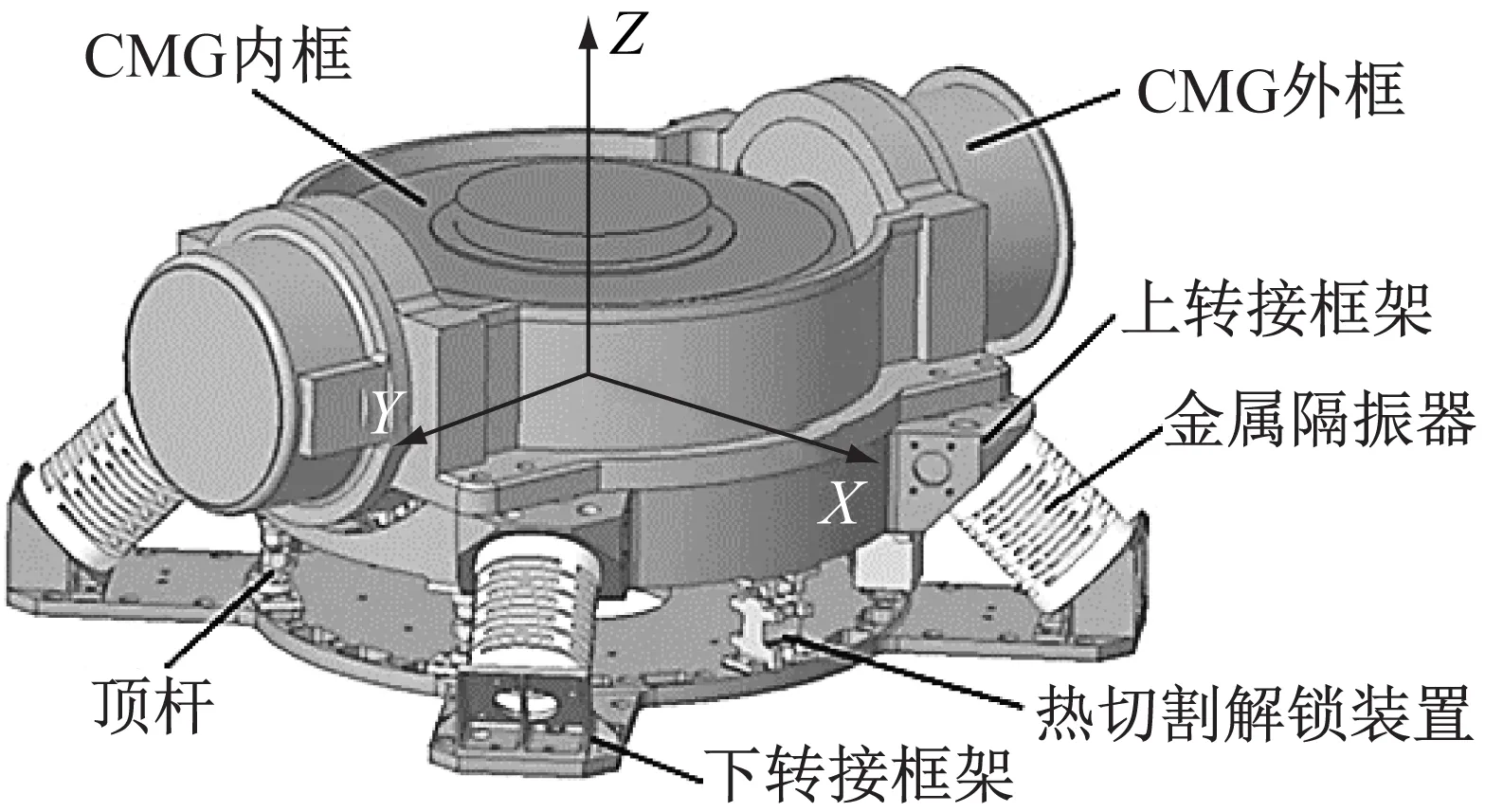
图3 隔振系统结构示意图Fig.3 The structure of vibration isolation system

基于上述被动隔振方式,柔性的隔振器在提供CMG微振动隔离的同时,也降低了CMG和卫星的连接刚度,使发射段CMG响应增大,超过CMG的单机许用环境。为解决这一问题,通常采用热刀解锁的方式将隔振装置锁定,在主动段通过锁紧装置锁紧上下框架以提高连接刚度和隔振子系统固有频率,在轨后再进行热刀解锁动作,使隔振器进入设计工况,实现CMG在轨隔振。

其中,金属隔振器的设计是整个隔振系统的核心,尤其刚度设计会直接影响到整个隔振系统的刚度和固有频率频点分布,由于横槽型隔振器是通过对称切割圆柱体所得,具有力学对称性好、设计参数少、易于参数化设计的优点,因此选择横槽型隔振器思路进行设计。

1.3 隔振系统参数设计

考虑到CMG的结构特点,采用四个完全相同的汇聚式布置隔振器支撑构成隔振系统,该种布置方式易于得到独立振动且具有良好的稳定性,根据图3所示的隔振系统构型,建立等效数学模型如图4[8-9]。将CMG和上框架视作统一整体,O为上框架下底面的中心,选择参考坐标系Oxyz作为平台的中心惯性主轴,四个隔振器连接点分别为A、B、C、D,各自轴线汇聚于点M。四个隔振器上端面中心点距离X、Y轴距离分别为a和b,四个隔振器采用对称布置,四个隔振器轴线与X轴(θ1)以及X-Y平面(θ2)成固定角度,且该角度对四个隔振器的表现一致。

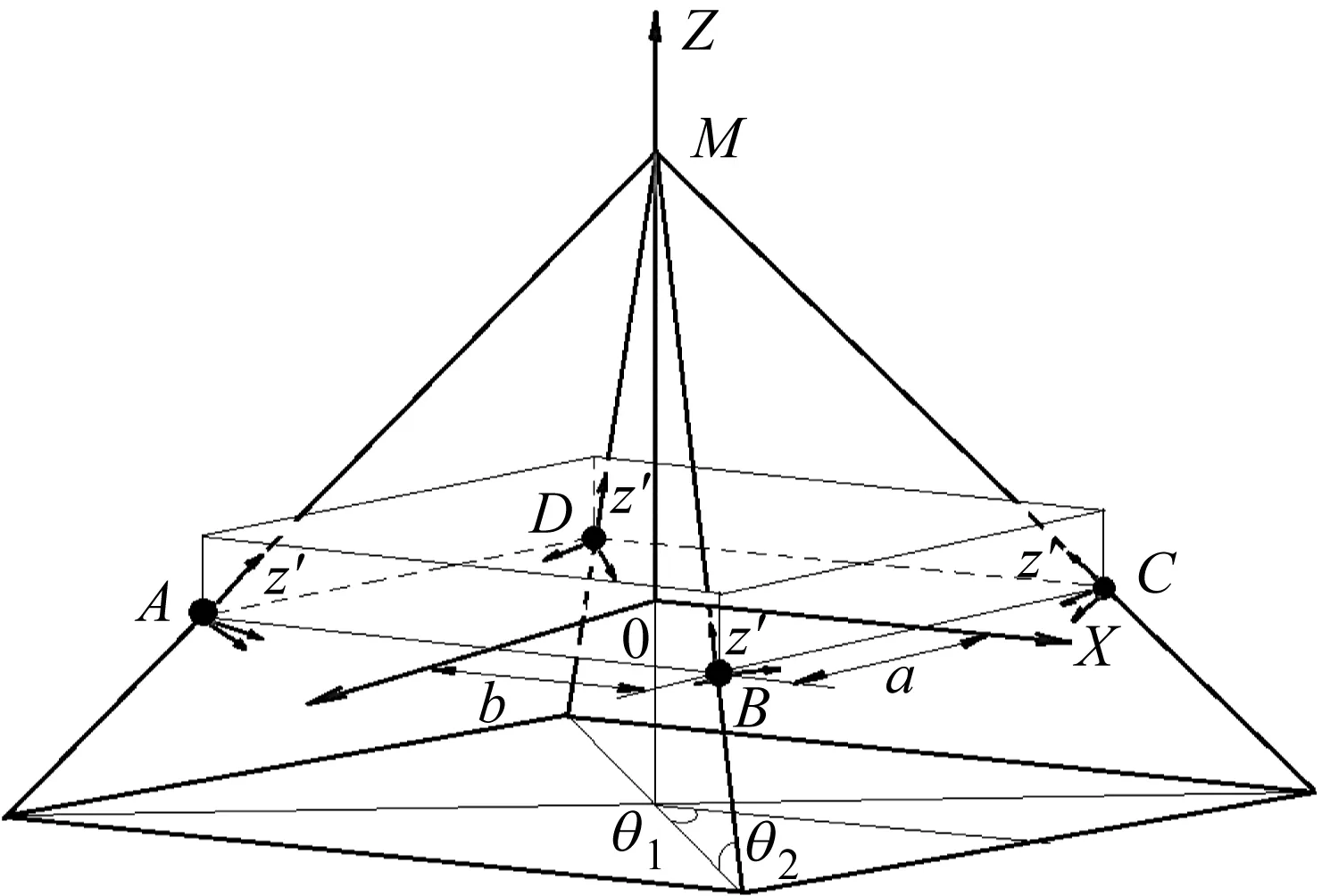
图4 CMG隔振装置数学模型Fig.4 The mathematical model of vibration isolation system

图5 横槽弹簧设计参数Fig.5 The structure of single isolation spring unit

(1)

式中:β为传递率,即响应幅值与输入激励幅值之比;f为任意频率,此处主要针对CMG产生的60 Hz扰动;fn为隔振系统频率;ζ为阻尼比,对金属隔振器可取值0.05[12]。

为保证60 Hz频点处隔振效果不低于85%,则fn应低于22 Hz,且隔振系统基频越低隔振效果越好,且优化隔振系统基频过程中,考虑1.3倍最低频率裕度[13],结合CMG在舱板的布局及工作环境要求,隔振系统基频应高于18 Hz,综上得到隔振系统基频应为18～29 Hz。同时考虑到整星环境下其他扰动频点,理想隔振系统的前三阶频率应在20～27 Hz之间,后三阶应在30～45 Hz或65～800 Hz之间,以避开干扰频点。根据以上分析,结合CMG机械接口特性、卫星安装空间等综合考量,经过大量仿真计算,选定a=b=190 mm,θ1=θ2=45°。

在横槽隔振器设计过程中,也采用参数化设计思路。为了明确不同的隔振器参数对其刚度的影响,将隔振器分为若干楔形块和环形条进行研究,参数包括外径D(参数1)、内径d(参数2)、楔块宽度t(参数3)、层厚度h(参数4)、层数n(参数5)。基于频率设计约束,经过多轮仿真迭代,最终隔振器设计参数定为:D=57 mm,d=43 mm,t=8 mm,h=3 mm,n=8 mm。

2 频率特性验证分析

为考察隔振系统频率特性,对隔振系统中的单个隔振器进行垂直刚度的仿真和试验测试,并对隔振系统进行模态分析和模态敲击试验。

2.1 隔振器垂直刚度仿真与验证

根据隔振系统的实际组成进行简化并建立有限元模型,利用ANSYS软件计算单个隔振器的垂直刚度。隔振器采用高阻尼材料锰铜合金,一方面,可以通过隔振器刚度设计实现抑制微振动扰动,另一方面,扰振源引起的微振动会在微观上引起阻尼材料振动变形,驱动材料内部微观高密度孪晶界面滑移运动,将机械能转化为热能,切段振动传播途径。如图6所示,仿真时对隔振器下端面设置固定支撑,并在上端面施加竖直向下的力,取杨氏模量为70 GPa,经计算得到隔振器垂直刚度为58.62 N/mm。

图6 单个隔振器垂直刚度仿真Fig.6 The FEA model of single isolator unit

通过拉力机,对28个样件进行垂直刚度测试,测试结果如图7所示。垂直刚度取平均值为59.18 N/mm,弹簧一致性较好,仿真结果与实测结果接近。

(a)

2.2 隔振系统模态分析

当卫星发射入轨后,通过热切割解锁装置完成CMG解锁动作,CMG内框在指定角度下内转子以6 000 r/min的转速工作,因此选CMG内/外框夹角(框架角)为45°、90°、135°、180°、225°、270°、315°的工况,如图8所示。根据实际情况建立有限元模型,并合理设置边界条件,通过ANSYS软件计算出不同角度下隔振子系统前六阶模态。如图9所示,当框架角为0度且CMG内转子静止时,隔振装置仿真得出的前三阶固有频率分别为19.105 Hz、20.644 Hz、24.353 Hz,当内转子转速设置为6 000 r/min时,前三阶固有频率为20.643 Hz、22.423 Hz、24.353 Hz,相应的振型分别为沿Y轴摆动(Y轴平动与绕X轴转动耦合)、沿X轴摆动(沿X轴平动与绕Y轴转动耦合)、沿Z轴平动。

(a) 框架角α=0°

(a)

在实验环境搭建完成后,在隔振装置表面设置传感器测点,并通过锤击法实测出不同工况的系统固有频率,表1记录了隔振系统在不同框架角下且内转子转速为6 000 r/min时,隔振系统的模态仿真结果和模态敲击实验结果,经过对比,有限元模型仿真计算的模态与试验敲击模态几乎一致,因此仿真模型有较高准确度和可信度。

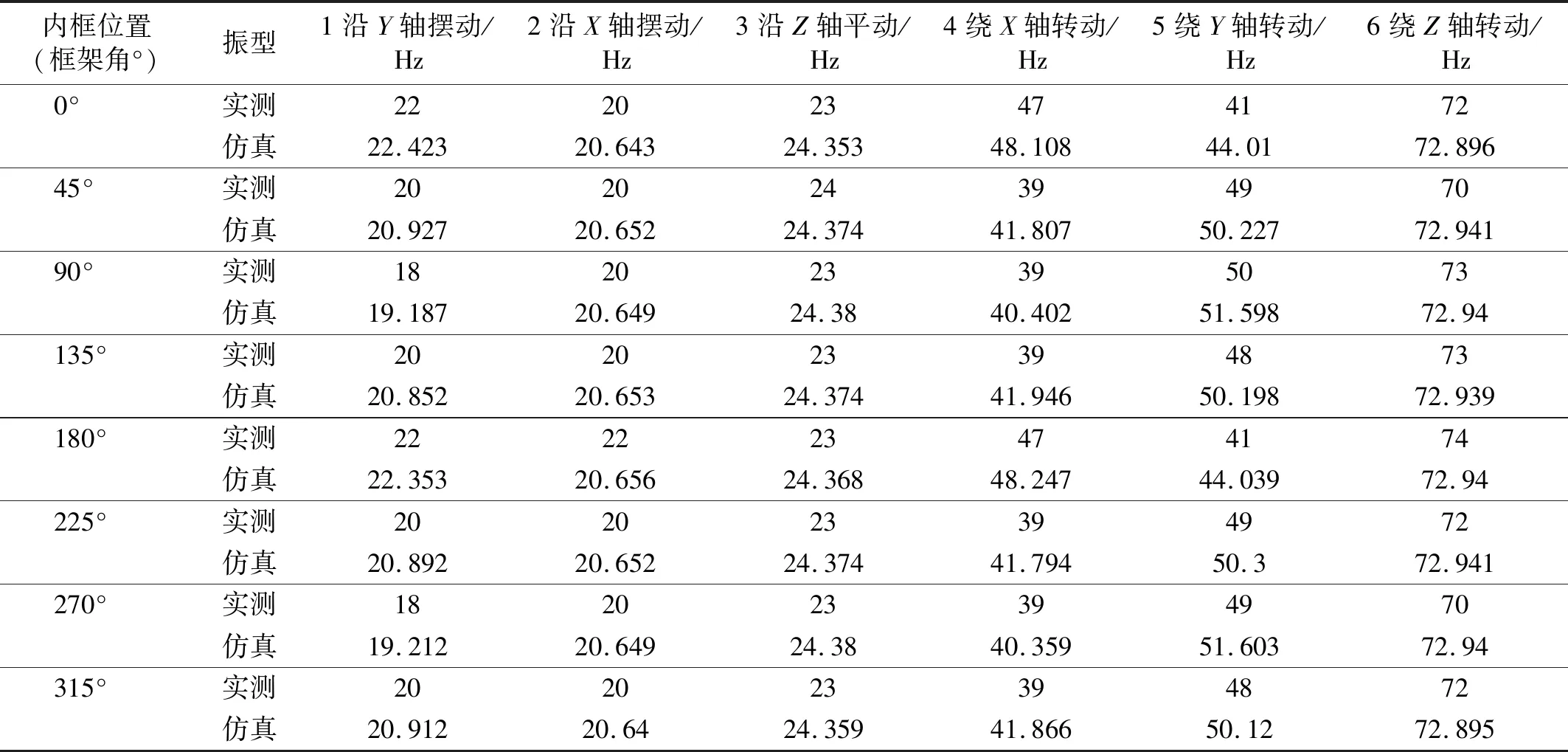
表1 隔振系统模态仿真结果及敲击试验结果Tab.1 The comparation of tested natural frequency and the simulated results

3 隔振效果验证分析

3.1 单机级力矩台微振动测试

在奇石乐力矩台上搭建微振动测试环境,试验装置示意如图10所示,隔振系统通过工装与奇石乐力矩台连接,CMG上表面设置4个加速度测点(测量在轨状态扰动输入),奇石乐力矩台测量系统输出的扰动力及扰动力矩。在锁紧工况时,隔振器被压缩,由限位顶杆支撑CMG,可视为刚性连接,因此实测数据为隔振前或无隔振效果的对照组,在热切割机锁装置完成解锁动作后,隔振器释放,CMG通过隔振器与结构件连接,此时实测数据为隔振后/有隔振效果的实验组。以0°框架角工况为例,分别从时域、频域对照隔振前/后(解锁/锁紧)两种工况的测试数据,以对隔振效果进行评估。

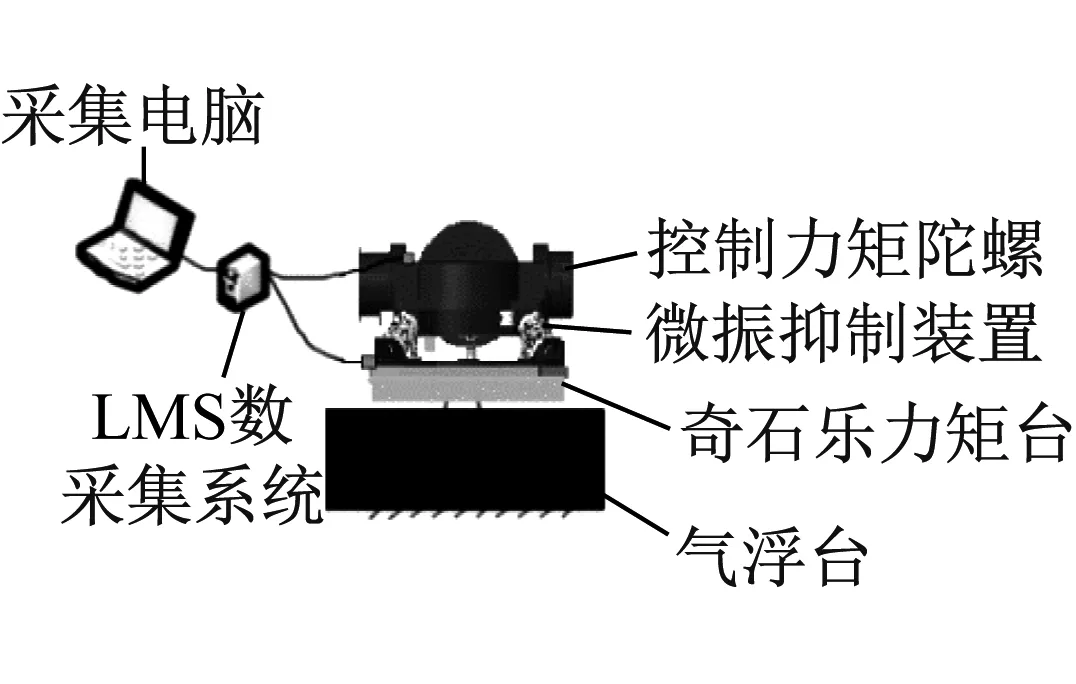
(a)

按照上述试验环境,4只加速度触感器设置于CMG外框上表面,隔振系统整体安装于奇石乐力矩台上,以实测得CMG产生的扰振加速度数据(即输入隔振系统的扰动加速度)和隔振系统安装面的扰动力、扰动力矩数据(即隔振系统输出的扰动力、扰动力矩)。表2为隔振系统解锁后实测结果数据汇总,图11为A1～A4加速度传感器实测的CMG扰振加速度时域、频域曲线。

表2 解锁工况CMG框架角为0°时,产生的扰振加速度数据Tab.2 The acceleration of working CMG when the turning angle is 0°under unlocked condition

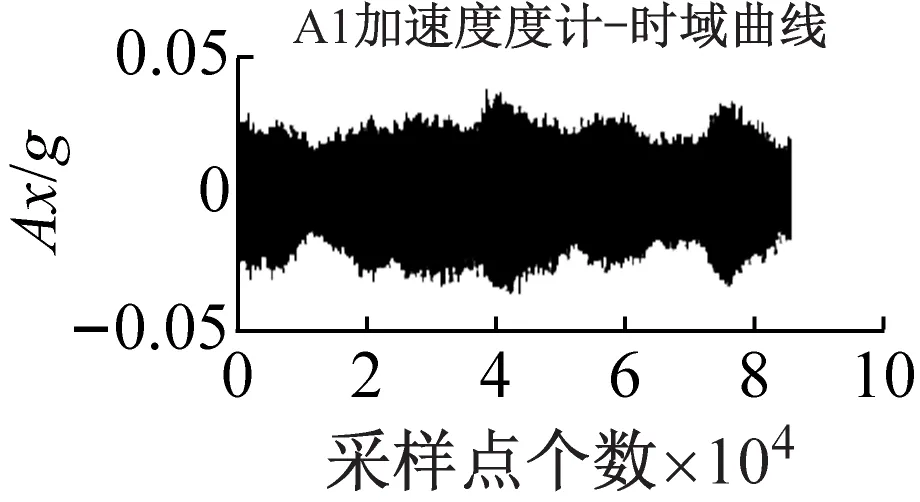
CMG框架角0°,内转子6 000 r/min,解锁工况

当隔振系统处于锁紧状态时,隔振器被压缩,由热切割解锁装置和顶杆支撑CMG,因此隔振系统提供刚性连接,奇石乐平台采集到的数据为隔振前系统输出的扰动力。当热切割解锁装置完成解锁后,CMG和舱板之间由隔振装置提供柔性连接,此时测得隔振后系统输出的扰动力。

表3对比了隔振系统解锁前后隔振系统输出的扰动力,从时域数据看,隔振装置对CMG产生的扰动在各个方向都有明显抑制效果,从频域来看,在59 Hz和100 Hz关键频点,尤其CMG扰动较大的X、Y方向都有明显抑制,扰振可衰减1个数量级以上。

表3 单机级微振动试验:CMG隔振系统力矩台测得扰动力隔振前/后(解锁/锁紧)效果对比Tab.3 The unit-level micro-vibration test:the output force of vibration isolation device

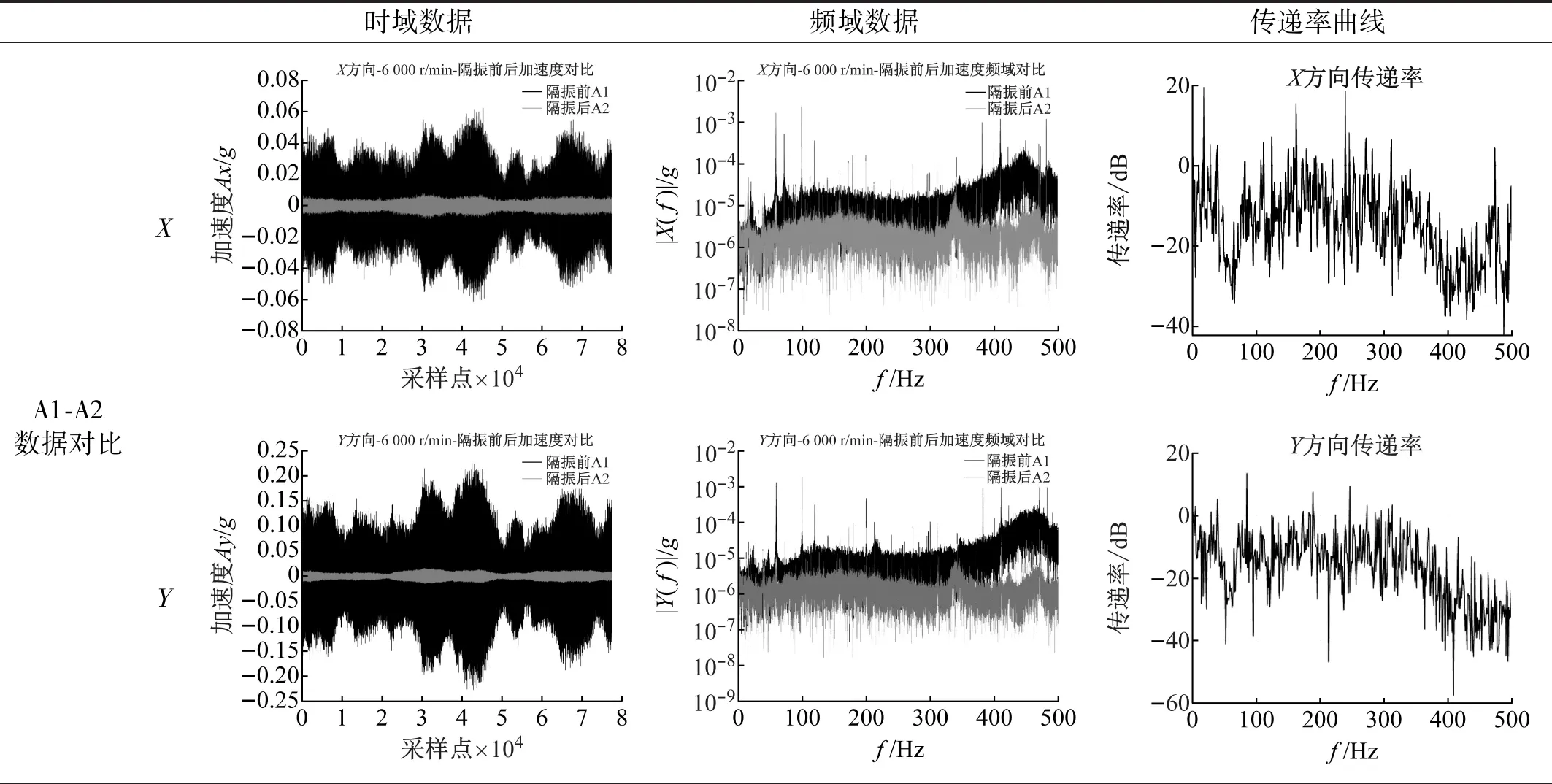
表4 整星级微振动测试加速度时域、频域对比结果Tab.4 The acceleration of vibration isolation device in time domain and frequency domain

3.2 整星级别微振动测试

CMG在卫星上采用竖直安装方式,将隔振系统安装在卫星舱板上,分别在CMG上表面和蜂窝板上安装加速度传感器,其中A1、A3安装在CMG表面上,A2、A4安装在下转接框架附近的蜂窝板上,如图12所示。以框架角0°为例,分析解锁工况下A1-A2数据以及A3-A4数据,可以对比隔振效果。

图12 整星级微振动测试加速度传感器测点布局Fig.12 The position of accelerometer in satellite-level micro-vibration experiment

与单机级测试数据相比,输入隔振系统的加速度量级无明显变化,重力方向对CMG扰振的影响较小。对下表时域数据RMS值分析,扰振源明显的X、Y方向上,隔振后加速度相较于隔振前衰减一个数量级,扰振量级较小的Z方向上,加速度也有60%以上的衰减效果,针对主要扰动频点60 Hz,在三个方向上隔振前扰动量级为10-3g,经衰减后可到10-5g,另一个主要扰动频点100 Hz处,扰动量级由隔振前的10-3g量级衰减到10-4g量级。

根据上述数据,整理分析后得到表5,从时域结果来看,在X、Y两个扰动大的方向,隔振效率达到85%以上,Z方向本身扰动小,隔振效率实现60% 以上的衰减,从频域角度看,在两个主要扰动频点60 Hz、100 Hz处,隔振效果均达到90%以上。

表5 CMG隔振装置隔振效果Tab.5 Effects of vibration isolation system

4 结 论

为降低CMG扰动群对光学载荷平台的影响,结合某型号卫星结构和CMG特性,提出了一种在多频率约束下的被动隔振系统设计方案,完成了卫星隔振器及装置的设计及研制。通过仿真分析和试验验证,CMG隔振装置固有频率分布合理,且不与整星结构、CMG发生动力学耦合,大大降低了CMG输出的扰动,具有明显隔振效果,与热切割解锁装置配合,可同时适用主动段和在轨段应用,表明该设计方法具有可操作性和有效性,对其他型号卫星的隔振装置优化设计具有参考价值。