一种考虑局部颈缩及损伤演化的改进失效准则在铝合金板冲击有限元分析中的应用

陈楚天,刘 斌,张晓丹,吴卫国

(1.武汉理工大学 绿色智能江海直达船舶与邮轮游艇研究中心,武汉 430063;2.武汉理工大学 船海与能源动力工程学院,武汉 430063;3.长江航道规划设计研究院,武汉 430041)

近年来,铝合金材料凭借比重小、比强度高、耐腐蚀性好等优越特性,已成为实现轻量化发展的理想材料之一[1],在工业中具有广泛的应用前景。相比钢材,铝合金材料发生屈服时无屈服平台,其真实应力应变关系亦可采用幂律硬化规律来描述[2]。然而,铝合金材料延展率较小,韧性较差,更易发生脆断。在安全性设计阶段准确预报铝合金结构的抗冲击性能是至关重要的[3]。

目前,有限元仿真方法广泛应用于结构冲击强度研究。对于大尺度薄壁结构,采用有限元仿真方法进行冲击分析时,主要采用壳单元,最小网格尺寸通常不小于板厚,对计算机性能要求较高,且计算时间较长。冲击区域局部网格细化可缩短计算时间,但网格过渡区域的网格易发生畸变,畸变单元易发生不合理的应力集中和失效。当冲击区域较大时,采用局部网格细化方法提高的计算效率有限。因此,针对大尺度薄壁结构,通常采用粗网格壳单元开展冲击仿真分析[4-6]。冲击裂纹的产生和扩展主要采用删除单元的方法来模拟,实际上,材料的颈缩、裂纹产生和扩展发生在一个比单元边长小得多的狭窄区域,因此粗网格通常无法捕捉这种局部现象[7]。虽然材料失效准则近年来得到了较大的发展,但仍具有很大的局限性,依旧难以运用粗网格来准确模拟裂纹的产生和扩展。国内外的众多学者针对钢质材料失效准则已经做了大量的研究工作[8-9],但针对于铝合金材料的失效准则研究较少,需要对此展开进一步的研究。

颈缩现象在金属和塑料材料的变形过程中十分常见。虽然近几十年来众多研究者分别从试验[10]、仿真[11]和理论[12]等多角度进行了大量研究,但目前尚未建立能够完全还原材料颈缩阶段动态响应过程的成熟数值模型。主要困难在于:①材料的真实应力难以直接通过试验获得[13];②材料厚度方向的收缩,引起应力分布偏离理想平面应力情况,给颈缩后的应变强化行为和断裂行为研究带来困难[14];③颈缩阶段的应变集中使试件出现应变梯度,可能引入尺寸效应[15]。

建立准确的材料弹塑性本构模型和失效准则,是有限元仿真正确分析结构抗冲击性能的关键。对于铝合金材料,通常可以采用现有的硬化模型对颈缩前段数据进行拟合,并根据拟合结果对颈缩后段进行外插,从而得到铝合金材料弹塑性本构模型。就预测材料断裂前的弹塑性响应而言,用壳单元进行数值模拟已经被证明是非常准确的[16]。然而,颈缩后的延性断裂预测对壳单元模型提出了挑战。当材料发生颈缩后,壳单元对延性断裂的预测无法保证足够的精度[17]。主要原因是:在颈缩阶段,材料的动态响应对网格尺寸非常敏感。为了克服壳单元这一缺陷,通常有两种处理方法,一种是以局部颈缩的发生作为失效条件,第二种是通过损伤演化模型来处理颈缩阶段。

Alsos等[18]结合Hill局部颈缩准则和Bressan-Williams剪切准则,以局部颈缩的发生作为失效条件,提出了基于应力的BWH失效准则,并采用试验和仿真相结合的方法证实了该失效准则能够很好预测钢质结构的颈缩和断裂行为。由于形式简单和参数易于校准,BWH失效准则在冲击工程领域得到广泛应用。

将局部颈缩的发生作为失效条件,由于完全避免了材料的颈缩行为,在某种程度上导致了材料的过早断裂预测[19]。因此,为快速准确分析铝合金结构在不同冲击载荷作用下的断裂失效行为,本文提出了一种由局部颈缩准则和损伤演化模型相结合的、参数易于校准且适用于粗网格的改进失效准则。该失效准则采用修订的BWH准则来预测颈缩的发生,颈缩发生后,通过将与网格尺寸相关的损伤演化模型与材料弹塑性本构模型相耦合,允许颈缩阶段材料屈服应力逐渐减小以补偿塑性应变软化效应,从而涵盖铝合金材料初始颈缩和最终破裂阶段,使得粗网格板材结构破坏过程的数值仿真具有较低的网格依赖性和合理的精度。

1 材料模型

1.1 材料弹塑性本构关系

在研究结构受外载荷作用下的变形和失效等问题时,首先要确定材料的本构关系,即应力应变关系。本文提出的材料模型服从J2塑性流动理论:各向同性硬化规律、Von Mises屈服准则、关联流动法则。

采用无屈服平台的幂律硬化规律对铝合金材料的塑性硬化行为进行描述,屈服应力σy的表达式如下

(1)

(2)

式中,σ0为初始屈服应力。

Von Mises屈服准则如下

(3)

进入塑性阶段,材料塑性应变服从关联流动法则。塑性应变张量计算公式如下

(4)

式中:εp为塑性应变;dλ为塑性流动率标量。

1.2 BWH准则的修订

BWH准则是基于材料遵循幂律硬化规律为前提推导得到的一种应力准则,用于预测材料颈缩的发生。因此,BWH准则理论上同样适用于铝合金材料。

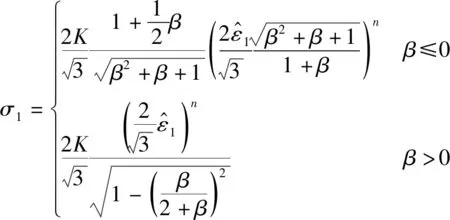
(5)

根据对Hill局部颈缩准则的分析,可对颈缩应变值进行合理的估计。为了提高BWH准则在铝合金材料冲击分析上的实用性,本文对BWH进行以下修订:

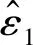
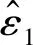
(6)

式中:l0/t0为单元初始长度与厚度的比值;d为撞头直径或边长。

1.3 损伤演化模型及失效判别

为了补偿材料塑性阶段的应变软化效应,避免应力突然下降引起的动态失稳,本文将Storheim等[26]提出的损伤模型运用于铝合金材料。由于该模型是基于颈缩处几何尺寸变化推导得到的唯象模型,其演化与材料的微观力学行为(空洞形核、生长和聚结过程)无关。因此该模型可用于不同的具有颈缩现象的材料。具体损伤函数如下

(7)

式中,〈-β〉=max(-β,0)。

(8)

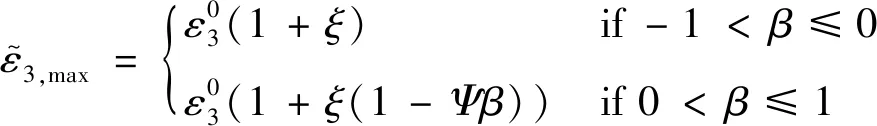
(9)

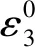
为了提高该失效准则的实用性,针对铝合金材料,建议ξ=0.15,Ψ=0.9。

经过修订,该失效模型仅包含2个未知参数:材料硬化参数K和n。这两个参数可直接由材料单轴拉伸试验得到的真实应力应变曲线拟合得到。因此,所提出的失效准则简单且易于校准,具有较高的实用性,可为铝合金结构抗冲击性能快速评估提供技术支撑。

2 材料模型数值实现

LS-DYNA是著名的显式通用非线性动力分析有限元程序,向用户提供了材料二次开发的功能,从而使用户可以根据需求自行开发材料模型。用户需要通过LSTC公司提供的专用于用户二次开发的动态链接库LSDYNA.LIB,连同用户编写的材料子程序一起在Intel Fortran Compiler中编译使用。用户编译成功后,生成新的可执行文件LSDYNA.EXE(求解器)。用户材料子程序的核心是单元的应力更新算法以及单元的失效判别算法。

2.1 应力更新算法

材料模型的应力更新包括弹性阶段和塑性阶段的应力更新。对于弹性阶段的应力更新采用广义Hooke定律计算。

C∶Δε

(10)

(11)

(12)

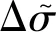
(13)

弹性应力计算完成以后,采用Von Mises屈服准则进行屈服判别,见式(3)。如果满足屈服函数f≥0,则材料进入塑性阶段。进入塑性阶段后,二维单元厚度方向的应变按照以下公式求解

εz=-(εx+εy)

(14)

对于塑性阶段的应力更新则采用径向返回算法。径向返回算法的核心思想是:首先对应力进行弹性预测,再对预测应力进行塑性修正,使应力沿屈服面法向返回到更新后的屈服表面,如图1所示。

图1 应力更新示意图Fig.1 Stress updating diagram

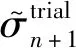
(15)

(16)

(17)

(18)

(19)

(20)

2.2 单元失效判断算法

应力更新完成后,用修订的BWH准则检查壳单元厚度方向的积分点是否发生颈缩。若检测到局部颈缩,单元开始进行损伤演化,更新损伤变量D。损伤变量在下一时间步将与材料弹塑性本构关系进行耦合。更新单元当前厚度方向的应变,若更新后的厚度方向的应变达到式(9)计算得到临界厚度应变值,则单元发生失效。

3 有限元分析与试验验证

3.1 试验介绍

基于团队已有的6组5083/H111铝合金板冲击试验[27],本文继续采用椭球形和方形撞头对5059/H116型铝合金板开展3组低速冲击试验。所有试验将用于验证改进的失效准则的适用性和准确性。9组工况如表1所示。铝合金板材料具体参数如表2所示。

表1 铝合金板冲击试验Tab.1 Impact test of aluminum alloy plate

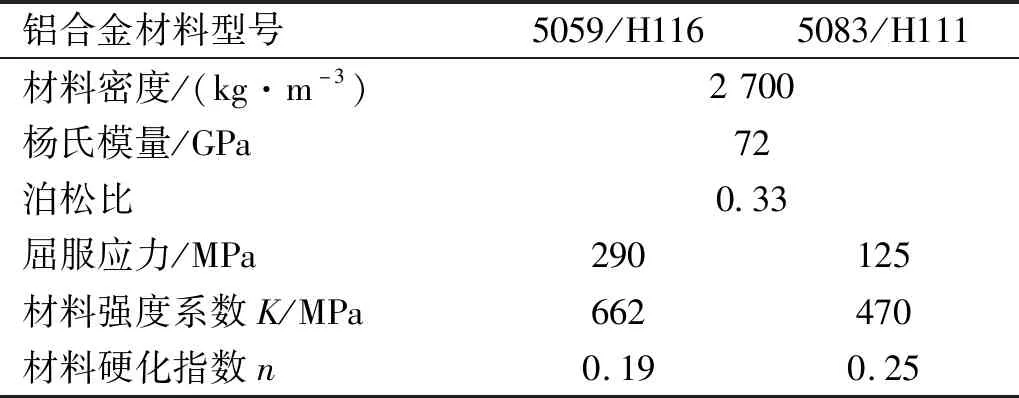
表2 铝合金板材料参数Tab.2 Material parameters of aluminum alloy plate

本次试验小尺寸试板厚度为4.0 mm,总尺寸为560 mm×400 mm,被试区域尺寸为400 mm×240 mm,四周开孔,试验中通过夹具将其夹持在水平冲击试验机基座,撞击位置为试板中心。试板加工图如图2所示。

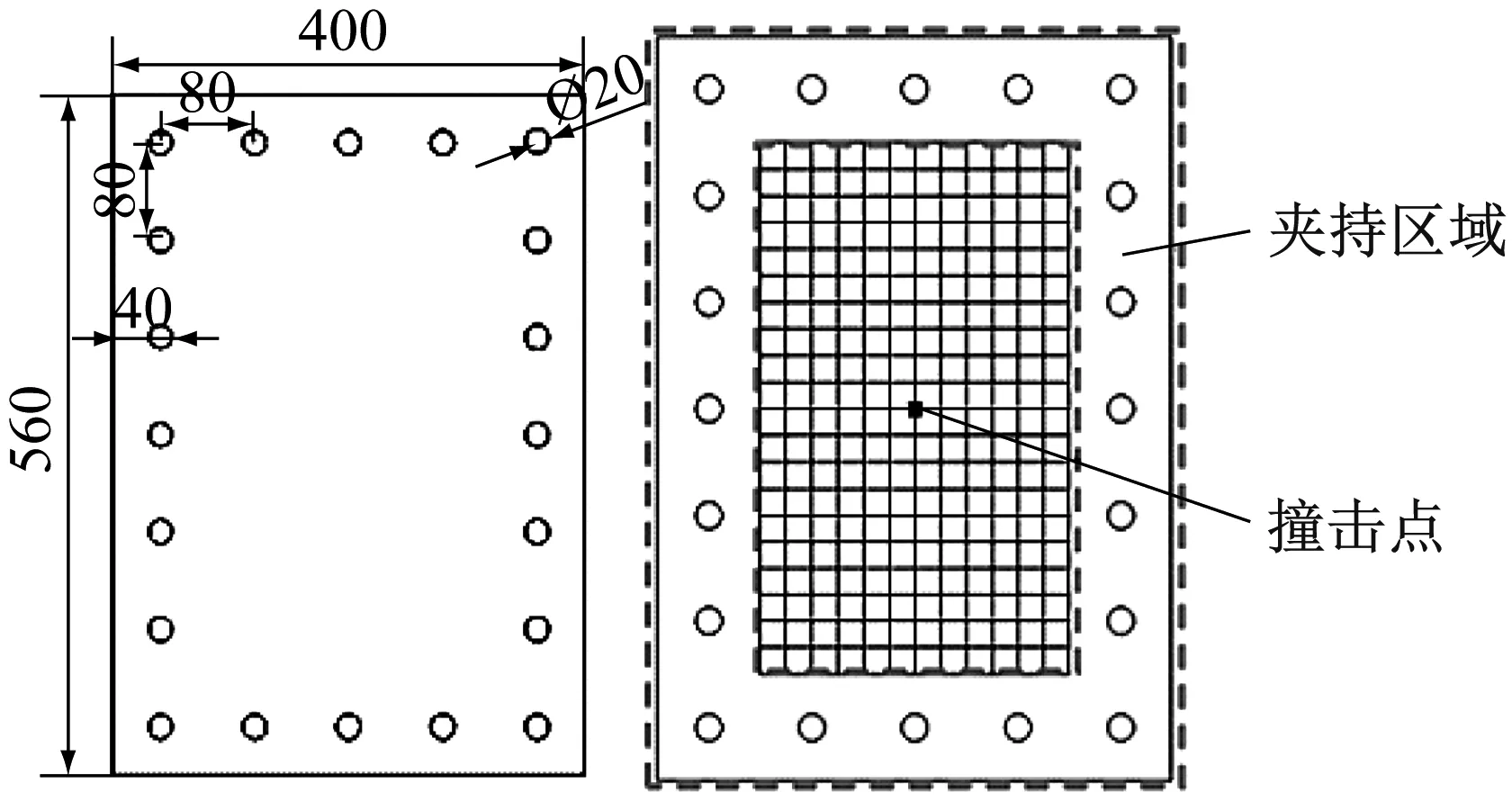
图2 试板加工图Fig.2 Processing diagram of test plate

冲击撞头如图3所示。椭球形撞头底部直径为80 mm,高80 mm。方形撞头的边长为10 mm。试验过程中,安装有撞头的冲击小车(总质量为100 kg)从滑轨上不同的高度处滑下以不同的动能撞击试板。记录小车初始撞击速度和加速度时程曲线数据,经数据处理可得到冲击力-变形曲线。

图3 撞头实物图Fig.3 Shape of indenters

3.2 有限元模型

为验证改进的失效准则的适用性和准确性,将第1章中所提出的由修订的BWH准则和损伤演化模型相结合的失效准则通过Fortran语言嵌入到LS-DYNA程序中,对铝合金板在四种不同撞头冲击作用下的9组试验进行有限元仿真分析。有限元模型如图4所示。

(a) 球形撞头

铝合金板采用四边形Belytschko-Lin-Tsay壳单元建模,在厚度方向定义五个积分点,材料选用自定义材料模型“Mat User Defined Material Models”。该材料模型采用所提出的由修订BWH准则和损伤演化模型相结合的失效准则。

撞头均由实体单元建模,材料选用刚性材料模型“Mat Rigid”,弹性模量和泊松比分别设置为210 GPa和0.3。通过增大密度的方法来确保其质量与试验撞头质量相同。撞头与铝板的接触定义为“Contact Automatic Single Surface”,摩擦因数为0.3。

边界条件由上下支撑板组成。上下支撑板均采用刚性材料模型“Mat Rigid”,弹性模量和泊松比分别设置为210 GPa和0.3。上、下支撑板完全刚性约束以模拟真实边界条件。

建立的有限元模型需采用第2章中二次开发生成的求解器求解。

3.3 有限元仿真结果分析

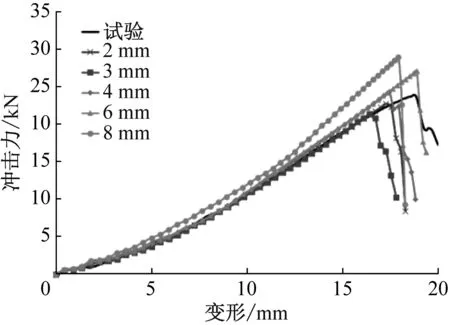
为研究不同网格尺寸对改进的失效准则精度的影响,选用多组网格尺寸对铝合金板在不同撞头冲击作用下的塑性破坏行为进行仿真分析。不同撞头冲击作用下的试验与仿真冲击力-变形曲线对比图如图5和图6所示。损伤对比图如图7～10所示。

(a) 直径为30 mm的球形撞头

(a) 直径为30 mm的圆柱形撞头

(a) 裂纹的产生与扩展

从图5和图6可以看出,铝合金板在不同撞头冲击作用下的冲击力-变形曲线与试验较好地吻合,表明所采用的材料本构模型能够很好描述铝合金材料的弹塑性力学行为。虽然不同网格尺寸仿真结果中材料破裂时的冲击力和变形与试验结果存在稍微差异,但平均误差均在10%以内,验证了改进失效准则的准确性。特别地,铝合金板在圆柱形和方形撞头冲击作用下材料破裂时的变形与试验基本重合,验证了式(6)的合理性。从整体上看,改进的失效准则在不同网格尺寸中均能较好地捕捉到铝合金板在不同撞头冲击作用下的塑性破坏行为,很好地再现了铝合金板在低速冲击载荷下的力学响应过程。

从图7～10可以看出,铝合金板在不同撞头冲击作用下的失效模式和裂纹形状与试验基本一致。从图7和图8可以看出,铝合金板在球形和椭球形撞头冲击作用下的失效模式以拉伸破坏为主。在冲击载荷下,试板在与撞头的接触面上产生局部凹痕。由于轴向的拉伸和厚度方向的压缩作用,试板逐渐减薄。板厚减小到一定程度,试板在局部凹痕内形成一个颈缩圈。最终裂纹起始于颈缩圈上的一点,并在撞头的推动作用下,沿着颈缩圈扩展。从图9和图10可以看出,铝合金板在圆柱形和方形撞头冲击作用下失效模式以剪切破坏为主。在冲击过程中,试板在撞头边界处产生局部应变集中,生成剪切带。最终裂纹起始于剪切带上的一点,并在撞头的推动作用下,沿着剪切带延伸。

(a) 验板正背面

(a) 裂纹的产生与扩展

(a) 试验板正背面

这说明改进的失效准则对铝合金材料裂纹的产生和扩展以及失效模式给出很好的预测。

从图7(a)和图9(a)可以看出,在相同冲击动能的情况下,由于接触面更小以及更加局部的应力集中,剪切带上的板厚方向受到的减薄作用比球形和椭球形撞头下的颈缩圈更加明显,导致剪切带上的板厚更早达到临界失效值,从而使试板更早失效。这表明铝合金板的断裂失效行为对撞头形状和尺寸异常敏感,从侧面印证公式(6)的合理性。

4 结 论

针对大尺度薄壁结构,采用非线性有限元方法进行冲击分析时对计算机性能要求较高,且计算时间较长。因此,为了提高计算效率,通常采用粗网格有限元模型进行分析。为了快速准确分析铝合金结构在不同冲击载荷作用下的损伤断裂行为,本文对钢质材料的BWH失效准则进行了改进以拓展运用于铝合金材料冲击分析,并结合损伤演化模型,提出了一种参数易于校准且适用于粗网格有限元模型分析的失效准则。

采用试验和仿真相结合的方法,将自定义失效准则在不同网格尺寸下的仿真结果与铝合金板在四种不同撞头冲击作用下的9组动态结构响应试验结果进行对比分析,无论是冲击力-变形响应还是局部损伤变形,均与试验结果较好地吻合。结果表明:

(1) 铝合金板的断裂失效行为对撞头形状和尺寸非常敏感。在相同冲击动能下,由于接触面以及局部应力集中的差异,铝合金板在圆柱形和方形撞头下的材料失效应变远小于球形和椭球形撞头。

(2) 改进的失效准则可运用于粗网格有限元模型分析,极大提高计算效率的同时准确预报铝合金板材结构在低速冲击过程中的塑性和破坏行为,可为铝合金结构抗冲击性能评估提供技术支撑。