一种多轴向耦合随机激励下缺口试件振动疲劳寿命预测方法

骆政波,范 鑫,刘 峰,陈怀海,郑荣慧

(1.国营芜湖机械厂安徽省航空设备测控与逆向工程实验室,安徽 芜湖 241007;2.南京航空航天大学 航空学院机械结构力学及控制国家重点实验室,南京 210016)

在航空、航天、交通运输以及机械工程等诸多领域中,结构在服役过程中经常处于振动环境中。结构长期在振动载荷作用下激发的动态响应可能会诱导其出现振动疲劳现象[1]。振动疲劳和常规静态疲劳的本质区别在于结构的动态应力响应是否被激发。振动疲劳失效是许多工程结构常见的失效形式,且结构发生的疲劳失效大多为多轴疲劳失效[2-3]。此外,实际振动环境通常是多轴向的,不同轴向振动载荷之间可能存在各种耦合关系,这样的耦合关系可能导致结构动态应力响应的耦合,从而对结构疲劳寿命产生影响。因此,多轴向耦合随机激励下结构的振动疲劳损伤机理值得深入研究。

金属结构在随机载荷下的疲劳寿命估计一直是科学界的一个难题,尤其是当载荷是多轴随机载荷[4-6]。从宏观层面上看,多轴疲劳准则方法可以分为时域准则和频域准则。时域多轴疲劳准则需得到结构部件局部应力分量时域历程,并结合多轴雨流计数法[7-8]和疲劳损伤累积准则[9-10]对其进行处理以估计结构部件的疲劳寿命。但是,为了获得可靠的统计结果,这种时域处理程序将变得十分耗时,这对工程应用是不利的。为了实现结构部件的疲劳寿命预测,频域多轴疲劳准则只需要在频域里处理局部应力应变功率谱密度函数,这不仅可以节省计算时间,还可以提供准确可靠的统计结果。频域多轴疲劳准则主要分为等效应力准则[11]、临界平面准则[12-13]和应力不变量准则[14-16],这三类准则在一些方面各有优缺点。

如果结构部件中存在几何不连续性(如缺口、圆角和孔洞等),则在随机疲劳载荷作用下,缺口附近会存在应力集中现象。这种现象会在局部区域产生非常高的应力梯度,从而产生更高的疲劳裂纹扩展驱动力。因此,缺口结构部件的疲劳损伤估计比光滑结构部件更为复杂。目前,缺口疲劳分析方法主要有名义应力法[17-18]、局部应力应变法[19-20]、应力场强法[21-22]和临界距离理论[23-25]。由于临界距离理论综合考虑了缺口根部应力梯度对疲劳裂纹萌生的影响,且具有计算过程简单和所需材料参数较少的优点,在工程领域受到广泛的认可和运用。

本文对具有U型缺口的LY12CZ铝合金试件进行了双轴向随机振动疲劳试验,并研究了两个振动轴向上载荷谱之间的相干性和相位差对缺口试件疲劳寿命的影响规律。此外,在Carpinteri-Spagnoli频域准则和修正临界距离理论的基础上,提出了一种多轴缺口疲劳寿命预测模型。该多轴缺口疲劳寿命预测模型既能考虑多轴随机载荷的非比例性对疲劳损伤的影响,又能考虑到应力梯度对缺口根部疲劳裂纹萌生的影响。同时,在临界距离理论的基础上引入了权重系数,量化缺口根部不同位置处应力对疲劳损伤参量的权重贡献,更加明确临界距离理论在计算缺口积分时的物理意义,从而提高缺口试件疲劳寿命的预测精度。

1 多轴缺口疲劳寿命预测模型

1.1 多轴向随机振动下结构动力学响应分析

为了模拟真实的振动环境,工程中一般采用振动台来实施结构部件的振动环境试验。在三轴向随机振动试验中,振动台提供的加速度基础激励可以用频域里的加速度PSD矩阵来描述

(1)

式中:矩阵对角项Gjj(f)(j:x,y,z)为各振动轴向加速度的自谱密度函数;矩阵非对角项Gjk(f)(j:x,y,z;k:x,y,z;j≠k)为各振动轴向加速度之间的互谱密度函数,并满足以下关系式

(2)

根据随机振动理论,结构的应力响应PSD矩阵可由加速度PSD矩阵和结构的应力频响函数矩阵计算得到

(3)

式中,上标‘T’为矩阵转置。Hσ(f)为结构的应力频响函数矩阵,Hσ(f)的一般形式可以表示为:

(4)

结合式(3)和式(4),可以将结构的应力响应PSD矩阵展开为:

(5)

由上式可以看出,各振动轴向上载荷谱之间的相干性和相位差可能会对应力分量之间的比例关系产生影响。

1.2 Carpinteri-Spagnoli频域准则

从分类来说,Carpinteri-Spagnoli频域准则[12]属于基于临界平面的多轴疲劳准则。

假设金属结构受到多轴随机载荷的作用,在PXYZ固定坐标系下结构中点P处应力向量的一般形式可表示为sxyz(t)=[s1,s2,s3,s4,s5,s6]T=[σx,σy,σz,τyz,τxz,τxy]T。应力向量sxyz(t)的单边应力PSD矩阵可以表示如下:

(6)

为了确定临界平面的位置,需要围绕固定坐标系PXYZ的坐标轴进行五次单轴依次旋转。前三次单轴依次旋转(即欧拉角φ,θ和ψ)可以定义一个旋转坐标系PX′Y′Z′,如图1所示。在旋转坐标系PX′Y′Z′下结构中点P处应力向量为sx′y′z′(t)=[s1′,s2′,s3′,s4′,s5′,s6′]T。可以计算得到应力向量sx′y′z′(t)的单边应力PSD矩阵

图1 通过欧拉角φ,θ和ψ定义的旋转坐标系PX′Y′Z′Fig.1 Rotation coordinate system PX′Y′Z′ defined by Euler angles φ,θ and ψ

Gx′y′z′(w)=CGσ(w)CT

(7)

式(7)中的旋转矩阵C=C(φ,θ,ψ)可以表示为

(8)

式中,cψ=cosψ,sψ=sinψ,cθ=cosθ,sθ=sinθ,cφ=cosφ和sφ=sinφ。

当改变欧拉角φ,θ(0≤φ≤2π,0≤θ≤π)时,在观测时间T内Z′方向上经历的正应力s3′(t)的极值期望值可以根据Daveport公式[26]计算得到

(9)

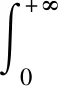
(10)

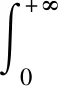
(11)

(12)

通过改变欧拉角ψ(0≤ψ≤2π),切应力s6′的最大方差值可以根据下式计算

(13)

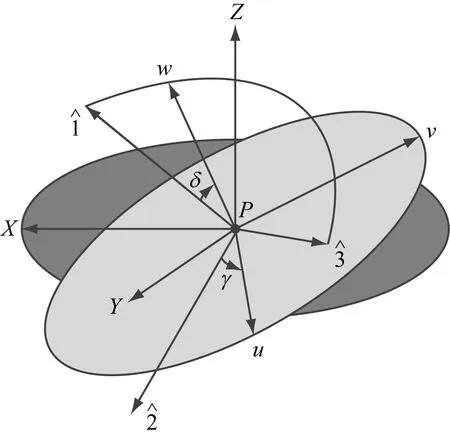
图2 通过欧拉角δ和γ定义的旋转坐标系PuvwFig.2 Rotation coordinate system defined by Euler angles δ and γ

(14)

(15)

式中,cγ=cosγ,sγ=sinγ,cδ=cosδ和sδ=sinδ。

临界平面的法线方向w可以通过偏离角δ(顺时针旋转)进行确定

(16)

而u轴和v轴通过方向角γ(绕w轴逆时针旋转)进行确定,其中u轴定义的是切应力s6″方差值达到最大值的方向

(17)

临界平面上P点处的等效单边应力PSD函数可以通过以下的线性组合表达式计算得到

(18)

式中,σaf和τaf分别为材料的弯曲疲劳极限和扭转疲劳极限。

对于单轴随机疲劳载荷,可以运用Tovo-Benasciutti公式[27]计算单位时间内的疲劳损伤强度

(19)

式中,Γ(·)为伽马函数;α2为带宽系数;vp为峰值穿越率;b为权重系数。b可以通过以下拟合公式计算得到

(20)

1.3 Carpinteri-Spagnoli频域准则拓展到多轴缺口疲劳

基于Neuber等[28-29]在19世纪50年代做出的开创性贡献,Bellett等[30]系统性地提出了临界距离理论。临界距离理论是基于两个基本假设提出的,一个基本假设是认为缺口附近服从线弹性应力场分布,另一个假设是认为缺口结构的疲劳损伤取决于缺口附近的应力场梯度分布。

根据临界距离理论,当缺口根部的有效应力Δσeff等于材料的单轴疲劳极限σaf时,缺口结构部件就处于疲劳极限状态。临界距离理论的计算示意图如图3所示。

(a) 点法

在实际运用过程中,临界距离理论可以具体表现为点法、线法、面法:

(21)

(22)

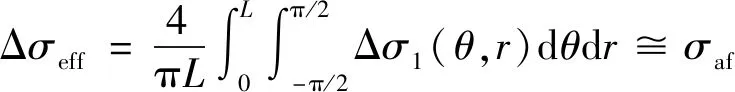
(23)

式中:Δσ1为缺口尖端前的最大主应力幅值分布;L为材料特征长度。L可以由以下关系式计算得到[31]

(24)

式中:ΔKth为应力集中系数门槛值;σaf为材料弯曲疲劳极限。

临界距离理论虽然考虑了缺口根部应力场梯度分布对疲劳损伤的影响,但是并未考虑权重影响,即不同位置处应力对疲劳损伤的权重贡献是不同的。因此,本文在缺口计算中引入权函数概念,认为权函数φ(r)代表缺口根部不同距离处应力对疲劳损伤的权重贡献应该是不同的。权函数φ(r)的具体表达式为[32]

φ(r)=e-(kt-1)r

(25)

式中,kt为缺口件的应力集中系数。

修正临界距离理论的表达式为

(26)

(27)

面法:

(28)

在本节中,将Carpinteri-Spagnoli频域准则和修正临界距离理论的点法和线法相结合,实现缺口结构部件在多轴向耦合随机激励下的疲劳寿命预测。该法主要分为三步:第一步是确定缺口结构部件的疲劳裂纹初始点;第二步是确定疲劳裂纹路径的方向;第三步是结合修正临界距离理论的点法和线法,运用Carpinteri-Spagnoli频域准则计算该点处的疲劳损伤值。

以图4所示的结构部件缺口来具体说明。假设疲劳裂纹初始点H是具有von Mises应力最大均方根值的节点,而疲劳裂纹路径是一条从裂纹初始点H发出且沿着缺口法线方向的直线。根据修正临界距离理论的点法,距离疲劳裂纹初始点L/2的疲劳临界点处疲劳损伤的修正值(运用Carpinteri-Spagnoli频域准则乘以权重系数)作为缺口结构部件的疲劳损伤值;根据修正临界距离理论的线法,在距离疲劳裂纹初始点[0,2L]区间范围内进行积分得到疲劳损伤的修正值(运用Carpinteri-Spagnoli频域准则乘以权重系数在区间范围内积分)作为缺口结构部件的疲劳损伤值。缺口结构部件的疲劳损伤具体计算公式如下

(a) 点法

(29)

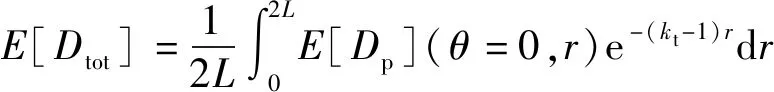
(30)

式中,E[Dp]是在P点处运用Carpinteri-Spagnoli频域准则计算得到的疲劳损伤值。

最后,缺口结构部件的疲劳寿命可以根据以下公式计算得到

(31)

2 试验研究

2.1 试验件及试验装置

缺口试验件所用的材料是LY12CZ铝合金,取自直径为12 mm的棒材。LY12CZ铝合金的机械性能参数和疲劳性能参数分别如表1和表2所示。

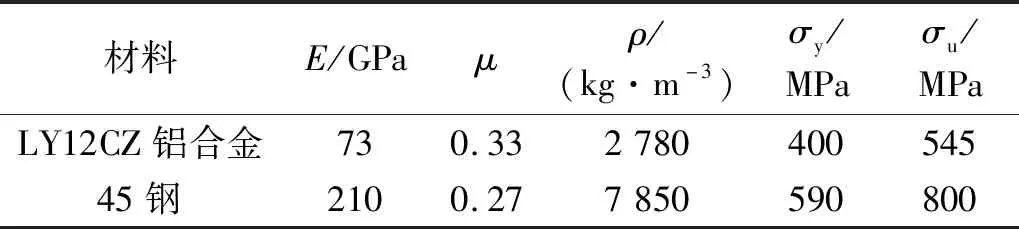
表1 LY12CZ铝合金和45钢的机械参数Tab.1 Mechanical parameters of LY12CZ aluminum alloy and 45 steel

表2 LY12CZ铝合金的疲劳参数[33]Tab.2 Fatigue parameters of LY12CZ aluminum alloy[33]

考虑到三轴向振动台的台面尺寸限制和试验量级限制,在试验件设计过程中采用有限元软件对试验件的尺寸、缺口位置和缺口深度进行了优化设计。最终确定试验件的几何尺寸如图5所示。采用数控线切割加工工艺对试验件进行加工,保证了试验件的尺寸加工精度和表面光洁度,从而降低试验数据的分散性。由图5可知,试验件的缺口深度为2.25 mm,缺口半径为1 mm,缺口试验件的弯曲应力集中系数kt,b=1.65和扭转应力集中系数kt,t=1.38。

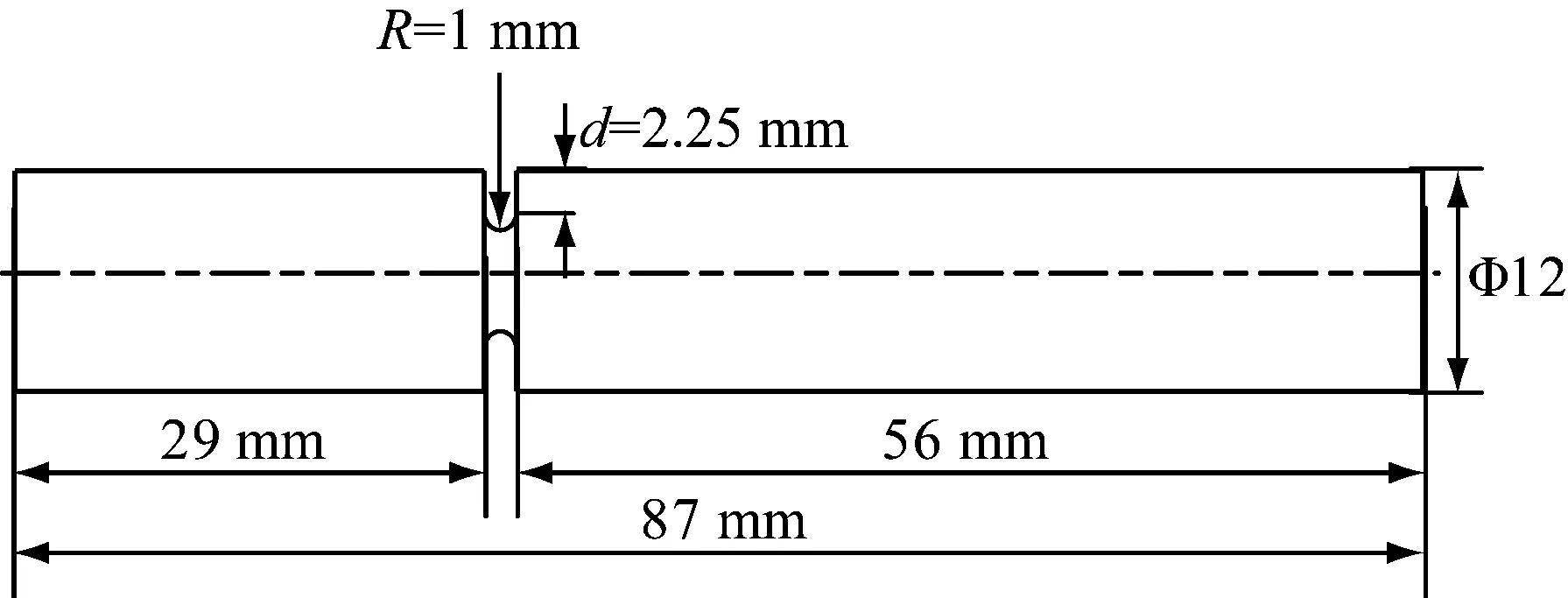
图5 LY12CZ铝合金试验件Fig.5 Test specimen made from LY12CZ aluminum alloy

试验装置由一个T型紧固部件和两个横向薄板(尺寸相同)组成。其中,横向薄板使用的材料为LY12CZ铝合金,而T型紧固部件使用的材料是45钢,它们的机械性能参数见表1。

试验装置和缺口试验件通过四个螺栓紧固联结形成一个整体试验结构,再通过夹具和底板安装在振动台面上,如图6所示。经过有限元软件优化设计,使得缺口试验结构的第一阶弯曲模态频率和第一阶扭转模态频率相差非常小,便于后续在双轴向随机振动疲劳试验中研究两个振动轴向上载荷谱之间的耦合关系对缺口试验件疲劳寿命的影响规律。

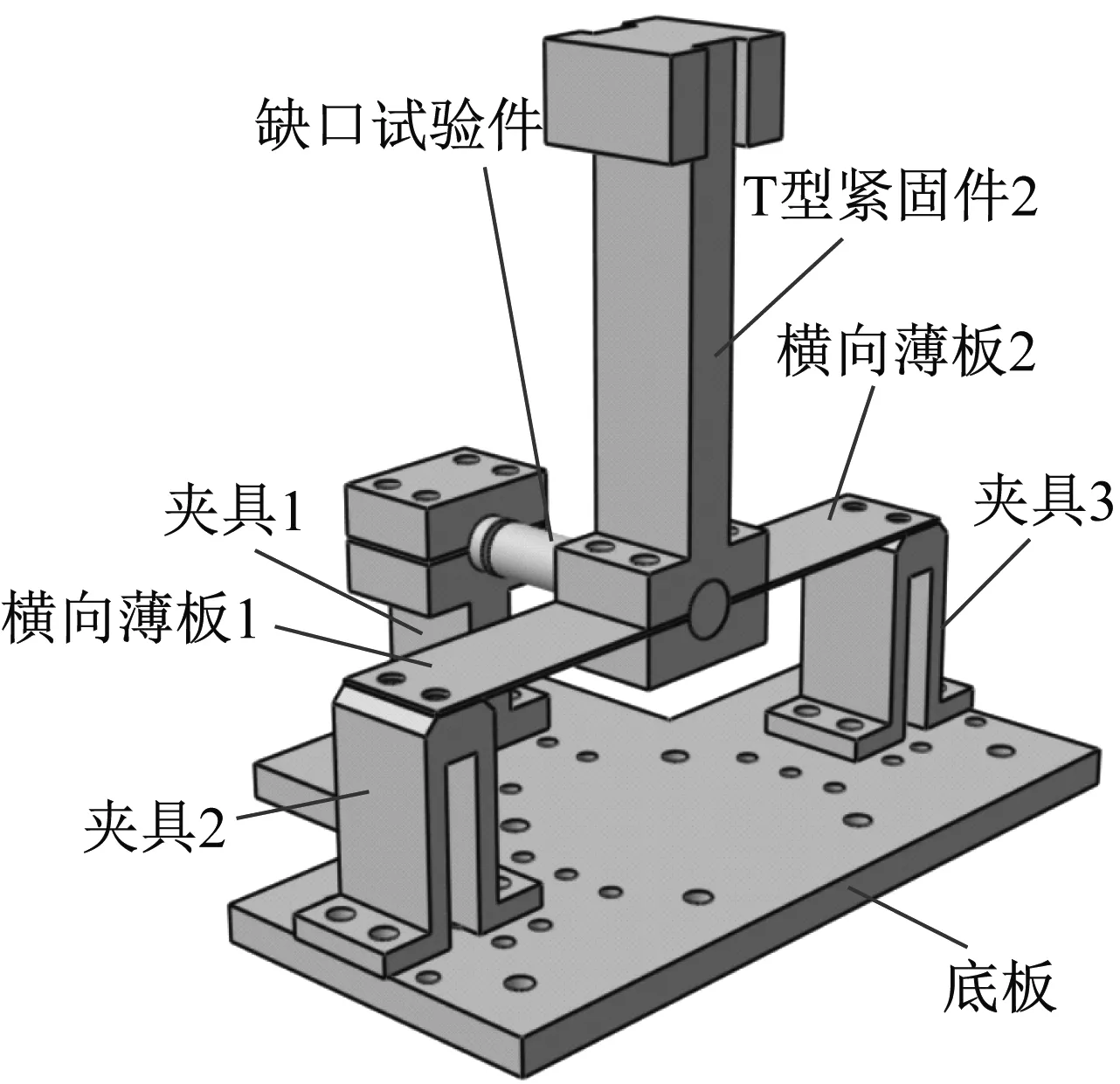
图6 试验结构安装示意图Fig.6 Installation diagram of the test structure

2.2 模态试验

为了确定加速度PSD矩阵的频带范围和获得缺口试验结构的模态参数,需要对安装在振动台面上的缺口试验结构进行模态试验。在本文中,采用锤击法对该结构进行模态试验,模态试验结果如表3所示。

表3 试验结构的模态试验结果Tab.3 Modal test results of the test structure

2.3 双轴向随机振动疲劳试验

缺口试验结构通过夹具和底板安装在G-6080-3HT-20型三轴向电动式振动台上。采用三轴向振动台对缺口试验结构实施双轴向随机振动疲劳试验。在双轴向随机振动疲劳试验中,由参考加速度PSD矩阵(如图7所示)生成的加速度时域信号同时施加在三轴向振动台的Y和Z轴上。

图7 加速度PSD矩阵Fig.7 Acceleration PSD matrix

安装在振动台面中心位置的三轴向加速度传感器可以对振动台面输出的加速度时域信号进行实时采集,并和三轴向振动控制仪相结合,实现对振动试验系统的闭环控制(如图8所示)。而分别安装在缺口试验件末端和T型紧固件末端的三轴向加速度传感器可以实时监测加速度动态响应,以便实时监测缺口试验结构的前两阶模态频率。在本文中,缺口试验件的振动疲劳寿命定义为结构模态频率下降5%所花的时间。

2.4 疲劳试验结果

在本文中,对缺口试验结构共进行了十二组双轴向随机振动疲劳试验。缺口试验件在不同振动工况下的疲劳寿命如表4所示。

表4 试验件在各工况下的振动疲劳寿命Tab.4 Vibration fatigue life of test specimens under different load conditions

由表4可知,在双轴向随机振动疲劳试验中,Y轴和Z轴两个振动轴向上载荷谱之间的相干性和相位差对缺口试验件疲劳寿命有非常显著的影响。

3 多轴缺口疲劳寿命预测模型验证

3.1 有限元仿真分析

缺口试验结构的有限元模型如图9所示,该结构由59 112个六面体网格单元和1 860个五面体网格单元组成,总共有64 664个节点。在网格划分过程中对缺口试验件的缺口进行局部加密,缺口区域内最小的单元尺寸设置为0.03 mm。

图9 试验结构有限元模型Fig.9 Finite element model of the test structure

在本文中,采用有限元软件PATRNA/NASTRAN 2010对缺口试验结构进行有限元仿真分析。通过模态分析可以得到缺口试验结构的前两阶模态振型如图10所示。通过图10和表2中数值和试验模态结果的对比可以发现:缺口试验结构的弯曲和扭转模态频率的相对误差分别是0.4%和0.9%。从而验证了缺口试验结构有限元模型建模的准确性。

(a) 第一阶模态(f1=80.8 Hz)

3.2 疲劳寿命预测结果

在本节中,运用Carpinteri-Spagnoli频域准则和修正临界距离理论的点法和线法相结合的多轴缺口疲劳寿命预测模型对缺口试验件在多轴向耦合随机激励下的疲劳寿命进行预测。

计算疲劳寿命Tcal和试验疲劳寿命Texp之间的对比如图11所示。在图11中,实线表示Tcal=Texp,而虚线和粗实线分别表示Tcal/Texp=0.5-2和Tcal/Texp=0.33-3。

(a) 点法

由图11可以看出:对于修正临界距离理论的点法,63%预测疲劳寿命落在试验疲劳寿命的2倍误差带内,而91%预测疲劳寿命落在试验疲劳寿命的3倍误差带内;对于修正临界距离理论的线法,86%预测疲劳寿命落在试验疲劳寿命的2倍误差带内,而100%预测疲劳寿命落在试验疲劳寿命的3倍误差带内。

3.3 讨论和分析

在本节中,对Y轴和Z轴两个振动轴向上载荷谱之间的相干性和相位差对缺口试件疲劳寿命产生显著影响的原因进行理论解释。

当缺口试验结构的弯曲模态频率和扭转模态频率相差非常小时,缺口试件中疲劳临界点处弯曲正应力和扭转切应力的主共振频带范围是重叠的。这样,当Y轴和Z轴两个振动轴向上载荷谱之间的相干性和相位差发生变化时,弯曲正应力和扭转切应力之间的比例关系会受到很大影响,从而缺口试验件的疲劳寿命也会受到很大影响;且弯曲正应力和扭转切应力之间的比例关系越强,缺口试验件的疲劳寿命也越长。

由表4和表5中对应工况可以看出,Y轴和Z轴两个振动轴向上载荷谱之间的相干性和相位差对弯曲正应力和扭转切应力之间的比例关系确实产生了较大影响;且载荷信号之间的相关性(载荷谱之间不同的相干性和相位差组合会产生不同的载荷相关性)愈强,弯曲正应力和扭转切应力之间的比例关系亦愈强,缺口试验件的疲劳寿命亦愈长。相干性相干性相干性相干性从而验证了前面的理论解释。

表5 各种载荷工况下应力分量之间的比例关系相干性Tab.5 Proportional relationships between stress components under different load conditions

有一种特例情况需要说明如下:通过比较表4中1号、4号、7号载荷工况和8号、11号载荷工况,发现当Y轴和Z轴两个振动轴向上载荷谱之间的相位差等于90°时,载荷谱之间的相干性对缺口试验件的疲劳寿命几乎没有影响。这是因为当两个振动轴向上载荷谱之间的相位差等于90°时,无论载荷谱之间的相干性怎么变化,Y轴和Z轴两个振动轴向上生成的随机加速度时域信号都是完全不相关的。这样,响应应力分量之间的比例关系就不受影响(由表5中1号、4号、7号载荷工况和8号、11号载荷工况可以直观看出,响应正应力和响应切应力是完全不成比例的),因此缺口试验件的疲劳寿命也不受影响。

4 结 论

本文基于Carpinteri-Spagnoli频域准则和修正临界距离理论提出了一种多轴缺口振动疲劳寿命预测模型。该多轴缺口疲劳寿命预测模型能同时考虑多轴随机载荷的非比例性对疲劳损伤的影响和应力梯度对缺口区域疲劳裂纹萌生的影响。此外,在临界距离理论的基础上引入了权重系数,量化缺口根部不同位置处应力对疲劳损伤参量的权重贡献,更加明确临界距离理论在计算缺口积分时的物理意义。

对LY12CZ铝合金缺口试验件实施了双轴向随机振动疲劳试验,研究了两个振动轴向上载荷谱之间的耦合关系对试验件疲劳寿命的影响,并从理论角度解释了其中原因。同时,运用提出的多轴缺口振动疲劳寿命预测模型对缺口试件在多轴向耦合随机激励下的疲劳寿命进行预测,结果表明该方法具有较好的预测精度,绝大部分结果都在3倍误差带内。

虽然本文提出的多轴缺口振动疲劳寿命预测模型对平面应力状态下的疲劳寿命预测具有较高精度。但是,对于更复杂的三向应力状态下的疲劳寿命预测精度,有待将来更多试验数据的验证。