半穿式应急钢桁梁上弦杆面外屈曲临界力研究

赵 曼,陈士通,孙志星,许宏伟,黄晓明

(1.石家庄铁道大学 土木工程学院,石家庄 050043;2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;3.石家庄铁道大学 大型基础设施性能与安全省部共建协同创新中心,石家庄 050043;4.石家庄铁道大学 河北省交通应急保障工程技术研究中心,石家庄 050043;5.东南大学 交通学院,南京 210096)

半穿式钢桁梁具有构造简单、拼组快速等特点,使其在桥梁应急抢修时成为应用较为广泛的桥型之一。但由于半穿式钢桁梁两侧上弦杆之间没有横向联结系,使用不当可能引发安全事故。19世纪末,半穿式钢桁梁破坏事故相继发生[1],为此,国内外学者针对半穿式钢桁梁面外屈曲问题陆续开展相关研究。Ziemian[2]进行了弹性支撑两端铰接压杆试验,给出了屈曲荷载计算的力学模型和计算公式;Hu[3]推导了半穿式梁上弦杆的屈曲临界力,结果表明能量法在此类复杂边界条件杆件的屈曲计算中应用良好;Timoshenko[4]在应用能量法求解屈曲临界力的同时,给出了上弦杆的屈曲半波数。Csagoly等[5-6]通过有限元方法证明了上弦杆轴力分布对屈曲临界力有影响;Iwicki[7]在研究中发现弹性支撑的分布对屈曲临界力有一定影响,但当弹性支撑数量较多时,其影响几乎可以忽略。段明德等[8]研究发现TBJ 2—1985 《铁路桥涵设计规范》中上弦杆临界力按杆件等轴力计算过于保守,应按抛物线分布进行计算;程高等[9-10]基于上弦杆等轴力条件,采用能量法推导了上弦杆面外屈曲荷载的解析表达式,给出了不同节间数时屈曲荷载的简化计算公式;孙纲廷等[11-12]将半穿式梁上弦杆简化为横向弹性约束的压杆,建立了等轴力条件下的稳定方程,并通过函数逼近,给出了简便实用的屈曲计算公式;温庆杰等[13-15]以阶梯形轴力分布和弹性支撑均布为前提,基于能量法推导了面外屈曲临界力的理论解。另外,JTS 152—2012《水运工程钢结构设计规范》[16]、JTJ 283—99《港口工程钢结构设计规范》[17]和TB 10091—2017《铁路桥梁钢结构设计规范》[18]给出了基本相同的屈曲荷载计算方法,通过查表确定杆件计算长度系数,再考虑杆件稳定折减系数可确定屈曲荷载。

综上可知,当前关于半穿式钢桁梁上弦杆面外屈曲的相关研究存在下述问题:①以弹性支撑连续梁为基本模型、采用能量法推导屈曲临界力为主要方法,但其推导过程中的假设与实际结构存在较大差别,如将上弦杆轴力简化为等轴力,致使结果偏于保守;②分析时多将上弦杆按一定间距布置的侧向支撑简化为均布形式,与实际结构不符,且节间较少时,计算结果偏大;③推导过程中的挠曲线方程采用多项三角级数,项数越多,屈曲临界力表达形式和计算过程越繁复,且包含多个不易确定的参数,不利于在实际工程中推广应用。鉴于当前半穿式钢桁梁上弦杆面外屈曲研究多限于上弦杆等轴力分布、均布弹性支撑条件、挠曲线方程复杂、计算方法实用性较差等问题,本文基于半穿式钢桁梁屈曲模态特征,对挠曲线方程进行适当简化,同时考虑不同的轴力分布和弹性支撑分布形式,建立4种平面计算模型,采用能量法分别推导4种模型的屈曲临界力解析解,并与整体模型开展对比分析,探究4种模型各自特点及适用性,旨在探寻一种合理且简单实用的屈曲临界力计算方法,便于工程推广应用。

1 基本模型

半穿式钢桁梁失稳模式通常表现为面外屈曲,根据其结构特点和屈曲模态,可将空间稳定性问题转化为平面问题,如图1所示为半穿式梁简化后的平面计算模型,将上弦杆视为两端铰接、中间设有若干弹性支撑的连续梁,图1中L为上弦杆总长度,d为节间长度,N为节间数,k为上弦杆侧向弹性支撑的刚度系数,x为半穿式梁跨长方向,y为半穿式梁上弦杆平面外屈曲方向,O为坐标原点,位于上弦杆左端。

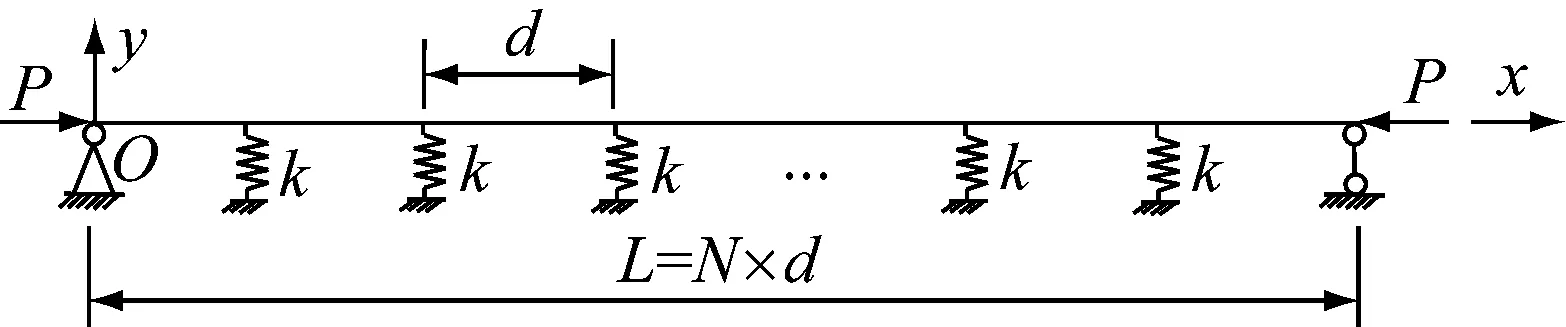
图1 半穿式钢桁梁简化计算模型Fig.1 Simplified calculation model for semi-through steel truss girder

为方便计算,半穿式钢桁梁上弦杆平面计算模型考虑以下基本假定:①上弦杆各杆件沿跨长为等截面;②上弦杆各节间距均相等;③侧向弹性支撑的刚度均相同;④由于端腹杆和端支座对上弦杆横向位移的约束作用明显强于中间区域,故将上弦杆端部视为铰接。

结构屈曲失稳时的挠曲线方程常采用若干项三角级数作为形函数,但这种表达形式过于复杂,不利于工程应用。本文根据不同跨径、不同荷载作用下半穿式梁的屈曲模态特点,将挠曲线方程简化为1项或2项三角级数。根据杆件轴力、侧向支撑以及挠曲线的不同形式将平面计算模型分为4种,如表1所示。

表1 不同平面模型的基本假定Tab.1 Fundamental assumptions of different plane model

1.1 平面模型Ⅰ

本模型除满足以上基本假定外,还需满足以下假定:①各杆件轴力均相等,且均以杆件轴力最大值计算;②侧向弹性支撑视为均匀分布的连续弹性约束;③由于结构和荷载基本对称,则屈曲模态也为对称形式,或正对称或反对称,且屈曲变形为多个半波时,其最大值相等。

此处,模型Ⅰ虽然采用了与文献相同的等轴力假定,但由于既有文献[11-13]中挠曲线表达式较为复杂,本文对挠曲线方程适当简化,如式(1)所示,以便于屈曲临界力的计算更加便捷和实用。

(1)

式中:n为屈曲模态的半波数,模态正对称时,n为奇数,反对称时,n为偶数;a为屈曲变形的最大值。

由式(1)求导得:

(2)

上弦杆屈曲时的弯曲应变能Ub为:

化简得:

(3)

由于侧向弹性支撑等效为均布连续弹性约束,且节间距相等,则均布弹性支撑刚度为k/d,侧向支撑应变能Uk为

化简得

(4)

外荷载P所作的功W为

化简得

(5)

根据能量法,上弦杆总能量U为

(6)

根据能量原理,当结构处于稳定的临界状态时,应满足

(7)

将式(6)代入式(7)即得

(8)

解方程式(8),可得弦杆等轴力、弹性支撑连续均布条件下,面外屈曲临界力Pcr的计算公式为

(9)

模型Ⅰ计算理论简单,但是侧向弹性支撑等效为均布连续支撑,与实际结构相差较大,尤其是节间和侧向支撑数量较少时,容易造成较大误差。

1.2 平面模型Ⅱ

1.2.1 屈曲临界力

本模型中侧向弹性支撑按节间距等距离散布置,共有(N-1)个侧向弹性支撑,其应变能Uk为

(10)

式中,xki和yki分别为第i个侧向弹性支撑的位置坐标和屈曲变形值。

式(10)化简得

(11)

由于本模型中轴力分布形式依然为等轴力,故弯曲应变能Ub、外荷载P作功W同模型Ⅰ,详见式(3)和式(5),由此可得上弦杆总能量U为

(12)

根据能量原理,结构处于稳定临界状态时的平衡方程为

(13)

解方程式(13),可得弦杆等轴力、弹性支撑等间距离散布置时,面外屈曲临界力Pcr的计算公式为

(14)

1.2.2 临界刚度kcr

由式(14)可知,半穿式梁临界力取决于上弦杆抗弯刚度EI、节间距d、节间数N、侧向支撑刚度k以及屈曲模态半波数n,其中半波数n的取值与结构特性有关。当半穿式梁基本结构确定后,半波数n主要取决于侧向支撑刚度k,当刚度k增加到一定程度,半波数则会增加1个,所以从理论上来分析,应存在临界刚度kcr[19],此时可能出现半波数为n或(n+1)的两种屈曲模态。由于结构基本参数相同,故在这两种半波数不同的屈曲模态下,结构屈曲临界力理应相同,由此即可求得临界刚度kcr。

设半波数为n时,屈曲临界力为Pcr1,则:

(15)

半波数为(n+1)时,屈曲临界力为Pcr2,则:

(16)

根据相同参数下,结构屈曲临界力相同,可得:

(17)

由式(17)可求得两个相邻半波数n和(n+1)之间的临界刚度kcr,为便于区分不同相邻半波的临界刚度,在此将其记为kcr,n,n+1

(18)

由式(18)可确定不同相邻半波数的临界刚度。在确定半穿式梁屈曲临界力时,应首先根据实际侧向支撑刚度k,初判屈曲模态的半波数n,再按计算公式求解屈曲临界力Pcr。

另外,模型Ⅰ也可基于同样原理推导临界刚度,但由于模型Ⅰ假定侧向支撑连续分布,与实际结构有一定差别,在此不再进行详细推导,只给出临界刚度最终的计算公式。

(19)

1.3 平面模型Ⅲ

模型Ⅰ、Ⅱ均假定杆件轴力为等轴力分布,与实际结构相差较大。半穿式梁杆件轴力实际上呈阶梯状分布,在此设上弦杆杆件轴力最大值为P,同时引入轴力系数αi表示各杆件轴力Pi与最大轴力P之比,则有

Pi=αiP

杆件轴力不等情况下,结构屈曲模态也将发生变化,与等轴力时挠曲线有一定差异,但当假定的挠曲线与实际挠曲线半波数一致时,其计算结果误差较小,故为简化计算,依然可假定变形曲线为

由于变形曲线没有变化,故弯曲应变能Ub和离散弹性支撑应变能Uk的表达式与模型Ⅱ完全相同,详见式(3)和式(10)。

因杆件轴力实际为阶梯状变化,故外力做功需重新计算,各杆件轴力Pi做功总和W为

化简得

(20)

将Ub、Uk和W代入能量表达式,并化简得

(21)

根据能量原理,可得结构稳定平衡方程为

(22)

化简并求解式(22),可得弦杆轴力不同、侧向支撑等间距离散布置时,屈曲临界力Pcr为

或表示为

(23)

式(23)即为变轴力情况下的屈曲临界力计算公式。当弦杆轴力相同时,Pi=P,此时各杆件轴力系数αi均为1,则有:

(24)

将式(24)代入式(23),可得:

(25)

比较式(25)和式(14)可知,两者完全相同,故等轴力模型Ⅱ可视为变轴力模型Ⅲ的一种特殊情况。由式(23)和式(25)可得变轴力屈曲荷载Pcr变和等轴力屈曲荷载Pcr等之间的关系式

(26)

在此引入轴力不等放大系数η,并令:

(27)

则式(26)可表示为

Pcr变=ηPcr等

(28)

各杆件轴力系数比αi可通过静力分析得到,代入式(27)即可求得轴力不等放大系数η,Pcr等可按等轴力情况计算,最后通过式(28)计算变轴力情况下的屈曲临界力Pcr变。

另外,根据结构实际侧向刚度为临界刚度时,两种半波数不同的屈曲模态下屈曲临界力相同,可推导出模型Ⅲ的临界刚度kcr,其最终表达式与模型Ⅱ的式(18)完全相同,故可根据式(18)确定模型Ⅲ的半波数n。

1.4 平面模型Ⅳ

模型Ⅲ挠曲线方程设为一项三角级数,与变轴力情况下结构失稳曲线有一定偏差,为获得更准确的结果,可将挠曲线方程设为

则:

(29)

上弦杆弯曲应变能Ub为

化简得

(30)

侧向弹性支撑应变能Uk为

化简得

(31)

各杆件轴力Pi做功总和W为

化简得

(32)

其中,

(33)

上弦杆总能量U为

U=Ub+Uk-W

(34)

根据能量原理,当结构处于稳定的临界状态时,应有

即:

化简得:

(35)

式(35)为一元二次方程,其较小解即为屈曲临界力,鉴于屈曲临界力与半波数取值有关,故欲求屈曲荷载,需首先确定半波数n和m取值。由于模型Ⅳ屈曲荷载计算过程繁复,不宜进行临界刚度的推导和计算,建议参考模型Ⅱ中式(18)计算临界刚度,并估算半波数n。当实际刚度和临界刚度相近时,可适当调整半波数以获得更准确的屈曲半波数。根据屈曲模态的对称性和三角函数特点,m可取为(n+2)或(n-2)。根据不同的n和m值,所求得的临界力会有所不同,其最小者即为屈曲临界力。

另可证明,若m取为0,则所得结果与模型Ⅲ相同,故模型Ⅲ可视为模型Ⅳ的特例。同时可通过对比模型Ⅲ、Ⅳ计算结果的差异,判断所假定的挠曲方程是否合适,如果计算结果仍然不能满足精度要求,可采用三项三角级数进行求解,或参考相关文献[13]进行修正。

2 验证与分析

上述4种平面计算模型,由于结构简化程度和挠曲线方程不同,故计算结果准确度也随之不同,且都存在不同程度的误差。下面以半穿式铁路应急钢桁梁为例,采用不同模型计算上弦杆屈曲临界力,并以整体模型计算结果为基准,通过对不同模型计算结果的对比分析,确定屈曲临界力计算的优选方法,以便在半穿式铁路应急钢桁梁设计中推广应用。

2.1 工程概况

铁路应急钢桁梁主桁采用无竖杆的三角形结构体系,主桁杆件有标准杆件和畸零杆件两种,可根据需要拼组不同跨径钢桁梁。中小跨径钢桁梁通常采用半穿式结构,主桁高h为6 m,主桁宽B为6.5 m,标准节间距d为6 m,辅以4 m节间距进行跨径调整,可拼组24 m、32 m、40 m、48 m、56 m和64 m等不同标准跨径的半穿式铁路应急钢桁梁,主桁弦杆均采用相同尺寸的双槽钢截面。图2为56 m跨铁路应急钢桁梁结构图,其他跨径半穿式梁的结构形式与之相同。

(a) 正面

2.2 整体结构的仿真分析

为全面考虑半穿式梁结构的整体效应,本文借助于有限元软件ANSYS建立不同跨径半穿式梁的三维整体模型,通过线弹性稳定分析[20],确定结构的屈曲模态和失稳荷载。图3所示为应急钢桁梁设计活载,为便于统一荷载工况,整体结构计算中仅考虑恒载和活载中随挂均布荷载进行组合,主桁、联结系和桥面系各杆件均采用3维铁摩辛柯梁单元beam189模拟[21],图4所示为56 m半穿式应急钢桁梁的有限元模型。

图3 半穿式应急钢桁梁设计活载Fig.3 Design live load of 56 m semi-through emergency steel truss girder

图4 56 m半穿式应急钢桁梁有限元模型Fig.4 Finite element model of 56 m semi-through emergency steel truss girder

图5为不同跨径半穿式梁的屈曲模态,由图5可知,不同跨径的半穿式梁,其失稳模式也不同,其中24 m半穿式梁表现为局部失稳,端部腹杆和风撑首先破坏,其他跨径半穿式梁均表现为上弦杆的面外失稳,屈曲模态半波数随跨径增加由1逐渐增加到3,表明在侧向支撑刚度相同条件下,屈曲半波数随节间数增加而有所变化。

(a) 24 m

表2为不同跨径半穿式梁屈曲分析的计算结果,表中屈曲临界力为失稳破坏时,上弦杆轴力最大值。由表2可知,不同跨径的线弹性稳定系数差别较大,随着跨径增大,稳定系数逐渐减小,但屈曲临界力除24 m跨外其他跨径差别不大,主要原因是荷载作用下,上弦杆跨中杆件受力最大,是半穿梁整体失稳的控制杆件,由于不同跨径弦杆截面尺寸和侧向支撑刚度相同,故结构处于失稳临界状态时,跨中杆件轴力均达到相同的临界值。另外,24 m半穿式梁因端部杆件局部失稳而破坏,原因是相比其他跨径半穿式梁,24 m跨径相对较小,故相同荷载引起的上弦杆轴力随之减小,稳定性相对提高。同时由于半穿式梁腹杆截面尺寸比弦杆尺寸小,因此腹杆通常先于弦杆而破坏,但由于稳定系数接近50,远高于结构作用荷载,故实际工程中,24 m跨径半穿式梁结构稳定性有足够高的安全保障,局部失稳不会发生。

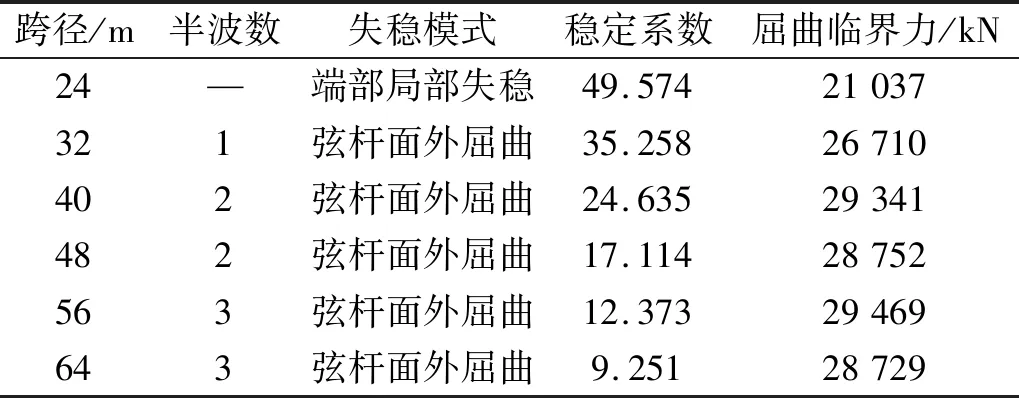
表2 不同跨径半穿式梁整体模型计算结果Tab.2 Calculation result of semi-through girder with different span

图6为不同跨径半穿式梁上弦杆轴力系数分布图,由图6可知,不同跨径的轴力分布形式大致相同,均呈抛物线规律变化,跨中杆件轴力最大,向两端逐渐减小。但是跨径越大,轴力分布越不均匀,钢桁梁设计时中可根据轴力分布规律选择不同的截面尺寸。

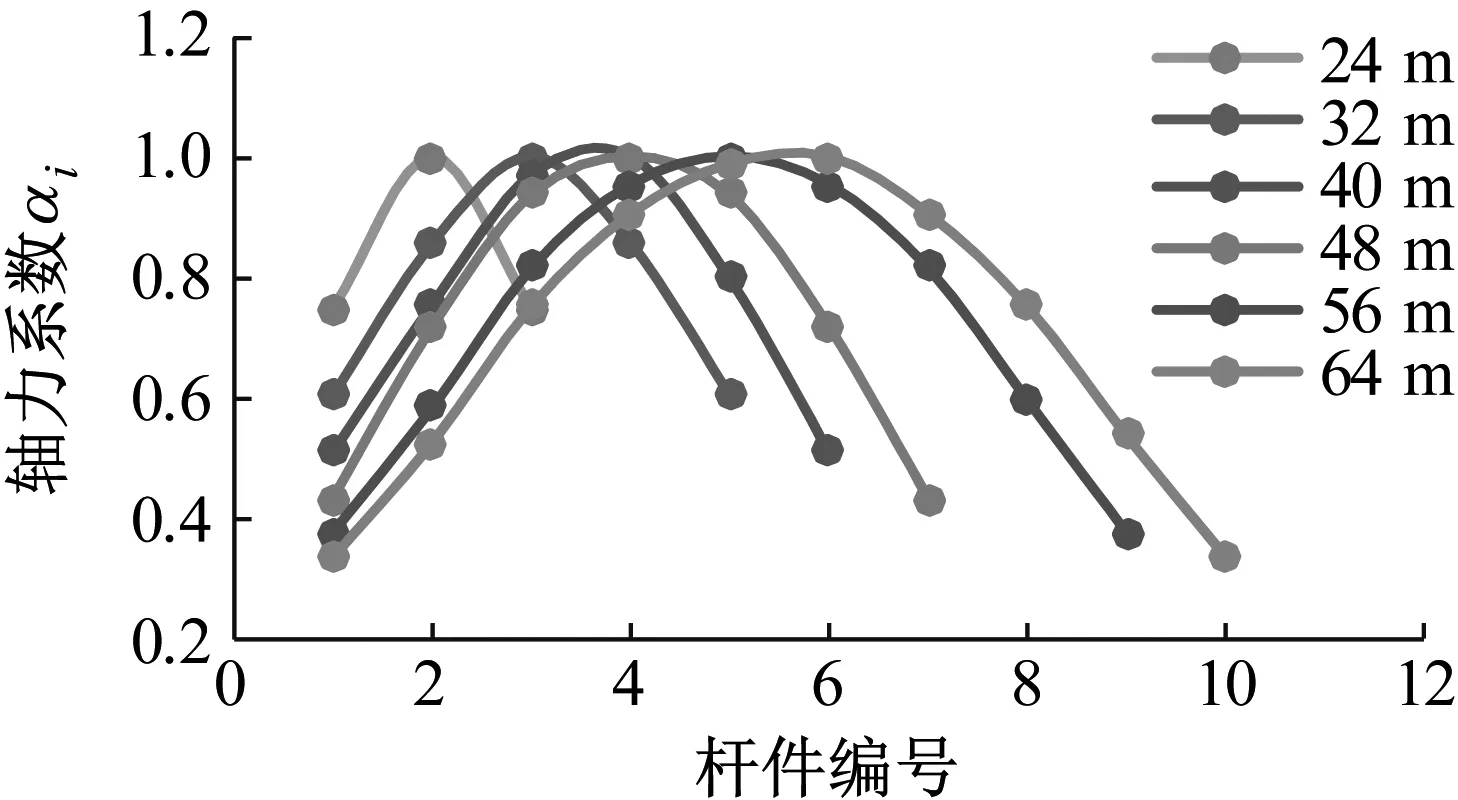
图6 不同跨径半穿式梁上弦杆轴力系数分布图Fig.6 Axial force coefficient of upper chord of semi-through girder with different span

2.3 基于平面模型的理论计算

2.3.1 计算侧向支撑刚度k

平面模型中侧向支撑刚度k由半框架提供,不同跨径铁路应急钢桁梁采用相同的半框架结构,同时为增强半穿式梁横向稳定性,在腹杆和横梁间加装了风撑,如图7所示。由于风撑对半框架受力影响显著,故在半框架受力分析中应考虑风撑的影响,可参考相关文献[12]进行计算。经计算,本文所示半框架在1 N单位水平荷载作用下的侧向位移为0.362×10-6m,上弦杆侧向弹性支撑刚度k为2.759×106N/m。

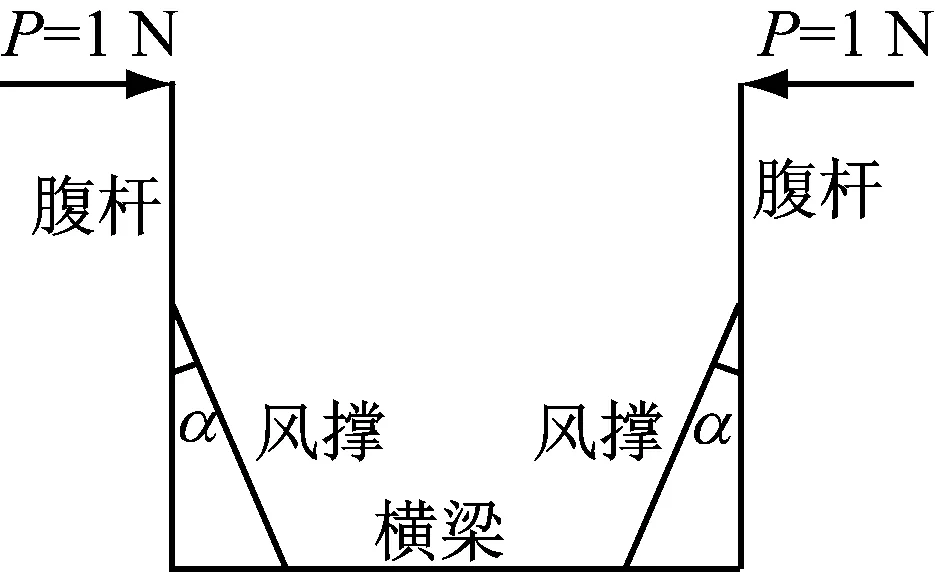
图7 半穿式钢桁梁半框架图示Fig.7 Semi-frame graphics of semi-through girder

2.3.2 计算半波数n

半穿式梁屈曲半波数的确定有2种方法:临界刚度法和根据规范查表法,在此主要介绍临界刚度法。首先,根据式(18)计算不同跨径半穿式梁不同相邻半波间的临界刚度kcr,然后将实际支撑刚度k与临界刚度kcr进行比较,即可确定半穿式梁屈曲半波数n。

根据规范和工程经验可知,半穿式钢桁梁屈曲半波数一般在1～5,故只需计算1和2、2和3、3和4、4和5四种相邻半波数的临界刚度,计算结果如表3所示。由表3可知,同一跨径的半穿式梁临界刚度随半波数增加而增加,不同跨径半穿式梁临界刚度随跨径逐渐减小。

表3 不同跨径半穿式梁的临界刚度与半波数Tab.3 Critical stiffness and half-wave of semi-through girder with different span

本文半框架提供的侧向支撑刚度k为2.759×106N/m,与临界刚度kcr进行对比,即可确定不同跨径半穿式梁的失稳模态半波数n,如表3所示。由表3可知,平面模型半波数可能与整体模型分析半波数有差别,原因是平面模型以经典欧拉梁理论为基础[22-23],没有考虑剪切对结构稳定性的影响,在一定程度上高估了结构的整体刚度,且平面模型是对整体结构的简化,很难全面考虑结构的空间效应;整体模型中采用的是铁摩辛柯梁理论,考虑了截面剪切、扭转变形对稳定性的影响,因此当实际支撑刚度k与临界刚度kcr相接近时,平面模型半波数与整体模型会有所不同,且平面模型半波数较大。

2.3.3 计算屈曲临界力Pcr

根据前面的侧向支撑刚度k和屈曲半波数n,分别代入4种平面模型计算公式,即可求得不同跨径半穿式梁的屈曲临界力Pcr,如表4所示。

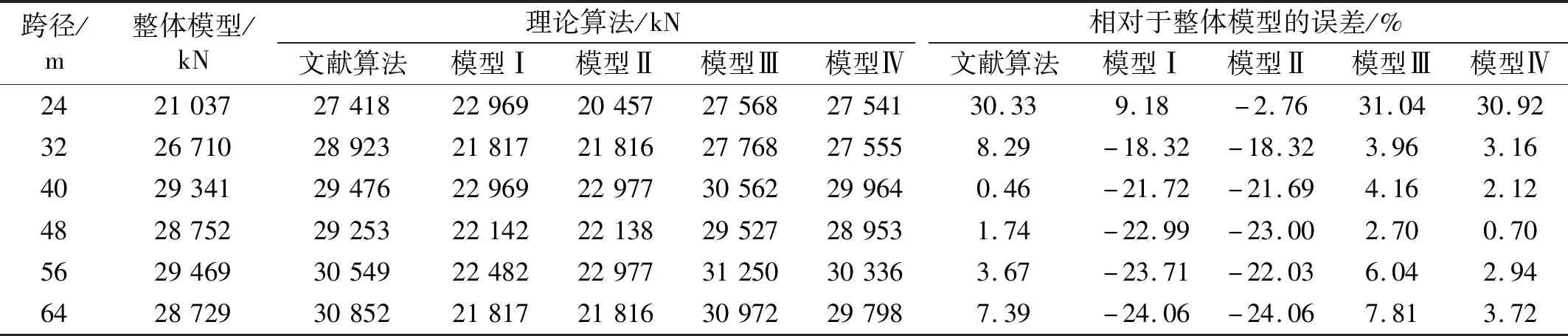
表4 不同模型屈曲临界力计算结果比较Tab.4 Comparison of calculation results of different models

由表4可知,模型Ⅰ、Ⅱ计算结果基本相同,由于两种模型均没有考虑轴力不等的影响,认为各杆件轴力与上弦杆最大轴力相同,故计算结果明显低于整体模型,误差为18%～24%,虽偏于安全,却过于保守,不宜直接作为屈曲临界力的计算方法;模型Ⅲ、Ⅳ计算结果相近,两种模型均考虑了上弦杆轴力分布不均匀的影响,故计算结果与整体模型相差不大,最大误差约7.81%,明显低于等轴力模型,因此屈曲临界力计算应优先考虑这两种方法。另外模型Ⅰ、Ⅱ与模型Ⅲ、Ⅳ结果差异明显,也表明了轴力分布形式对结构屈曲临界力影响很大,稳定分析中应考虑杆件轴力的实际分布特点,不能简单的按等轴力处理。

模型Ⅲ、Ⅳ计算结果虽然相近,但相比之下,模型Ⅳ误差更小,最大误差只有3%,与整体模型结果更接近,计算结果更准确,其原因在于两种模型采用的挠曲线方程不同,模型Ⅲ采用1项三角级数,模型Ⅳ采用2项三角级数,模型Ⅳ与整体结构屈曲变形曲线更接近,因此就准确度而言,模型Ⅳ最优,不仅考虑了轴力不等、弹性支撑的离散性,且挠曲线方程与实际屈曲变形的吻合度更高,故计算结果更准确。不足之处是计算公式繁复,在工程实用性方面略逊一筹。模型Ⅲ计算结果虽然相比模型Ⅳ误差略大,但依然可满足工程计算精度要求,也可作为屈曲临界力计算的优选方法。而且该法计算公式简单,可通过对等轴力情况下临界力Pcr等进行修正得到准确度较高的结果,因此综合考虑计算准确性和工程实用性,建议采用模型Ⅲ的计算公式作为半穿式梁屈曲临界力的简化计算方法。

为了进一步验证本文算法的准确性和实用性,本文采用文献[13]的方法计算了不同跨径半穿式梁的屈曲临界力,见表4。通过计算结果的对比可知,模型Ⅲ与文献算法的结果非常接近,最大误差只有4.33%。鉴于两种方法均考虑了轴力不等的影响,但文献算法中由于变形曲线假设为多项三角级数,使屈曲临界力计算非常繁复,实用性较差,相比之下本文模型Ⅲ的计算方法更简洁。

另外,24 m半穿式梁理论计算结果有些异常,原因是整体模型中24 m半穿梁失稳是由端部杆件破坏引起,而平面模型是按整体失稳考虑的,因此整体模型和平面模型计算的前提条件不同,故计算结果差异很大,两种结果的对比也没有意义。除此之外,还注意到24 m跨的模型Ⅰ和模型Ⅱ计算结果差别很大,原因是24 m跨半穿式梁上弦杆只有3个节间,2个侧向支撑,将离散的侧向支撑等效为连续均布形式与实际结构相差太大,因而计算结果不准确,建议中间支撑数<4,即节间数N<5时,侧向支撑按离散布置考虑。

综上所述,不同跨径半穿式梁不同算法的计算结果对比表明,基于变轴力条件的模型Ⅲ计算方法既准确又实用。本文的简化算法有助于工程设计人员快速而准确地选取半穿式梁杆件截面,为后续数值模拟提供便捷,因此本文算法对半穿式应急钢桁梁的设计有重要意义。

3 结 论

本文将半穿式钢桁梁上弦杆简化为侧向弹性支撑下的连续梁,采用能量法推导了4种不同平面计算模型的屈曲临界力解析解,通过与不同跨径半穿式钢桁梁整体模型和文献算法计算结果的对比,探讨了各平面模型的优缺点及其适用性,最后给出了便于工程应用的优选方法,主要结论如下:

(1) 建立了等轴力与不等轴力、均布连续与均布离散弹性支撑以及不同挠曲线方程下的稳定方程,给出了不同情况下屈曲临界力的解析解。

(2) 以等轴力、离散弹性支撑条件下的模型为基础,推导了相邻半波数之间的临界刚度计算公式,给出了屈曲半波数的确定方法。

(3) 建立了不同跨径半穿式钢桁梁的整体模型,分析了不同跨径半穿式梁的线弹性稳定系数、屈曲模态和失稳轴力,结果表明:随着跨径增大,线弹性稳定系数逐渐减小,屈曲模态半波数有所增加,但失稳时上弦杆最大轴力基本保持不变。

(4) 相比整体模型和文献算法,基于等轴力条件的模型Ⅰ、Ⅱ计算结果明显偏小,过于保守,不宜直接采用;基于变轴力条件的模型Ⅲ、Ⅳ计算结果与整体模型相接近,计算精度均可满足工程需要,但模型Ⅳ计算过程繁复,而模型Ⅲ计算简单,可通过对等轴力计算值的修正获得准确度较高的结果。综合考虑准确性和实用性,建议采用模型Ⅲ作为屈曲临界力计算的首选方法。