极端波浪作用下跨海箱形桥梁上部结构流固耦合特性研究

2023-09-20杨志莹屈建强

振动与冲击 2023年17期

黄博,唐尧,杨志莹,祝兵,屈建强

(1.重庆交通大学土木工程学院,重庆 400074;2.西南交通大学土木工程学院,成都 610031;3.重庆城投基础设施建设有限公司,重庆 400000)

“海洋强国”战略的提出推动了我国桥梁建设向深海和远海发展,跨海桥梁已成为国家“一带一路”战略中“21世纪海上丝绸之路”的重要组成部分[1-2]。杭州湾大桥、青岛大桥、舟山跨海大桥、港珠澳大桥的建成通车,以及琼州海峡、渤海湾和中国台湾海峡等跨海通道的酝酿规划,标志着未来将会有更多的跨海桥梁在复杂海域中兴建[3-5]。在我国跨海桥梁工程中,箱型截面的桥梁上部结构因其抗弯和抗扭刚度大、重量轻、整体性强、施工稳定性好等特点被广泛采用,例如已建成的港珠澳大桥和平潭海峡公铁两用大桥均采用箱型截面作为主要的上部结构形式[6-9]。

相比于跨越陆地江河的桥梁,跨海桥梁桥址区往往水深、浪高、流急,海洋环境相对复杂。此外,近年来全球气候变暖导致自然灾害频发,据统计显示,平潭海峡公铁两用大桥建设期间平均每年要经历6次以上的台风灾害,桥址区百年一遇浪高可达9.69 m[10]。极端海洋波浪的侵袭会严重影响跨海桥梁的施工安全,直接威胁到跨海桥梁结构运营及行车安全。因此,加强极端波浪作用下跨海箱形梁桥安全问题的研究迫在眉睫,针对其流固耦合关键问题进行深入研究对构建现代化高质量国家综合立体网具有重要意义。

极端海况下,波浪荷载已成为跨海桥梁结构设计和建设运营的主要控制荷载。飓风Ivan和Katrina分别于2004年和2005年在美国墨西哥湾附近登陆,造成至少44座桥梁在飓风和风暴潮所引起的极端波浪作用下被完全掀翻或者产生落梁破坏,此后跨海桥梁的极端波浪荷载致灾问题受到越来越多的研究学者关注。Douglass等[11]通过受损桥梁的灾后调研,基于前人研究成果提出了估算桥面板所受极端波浪荷载的经验公式。为探究跨海桥梁的极端波浪作用特性,众多研究学者相继开展了一系列的波浪水槽模型试验与数值仿真研究。Cuomo等[12]进行了比尺为1∶25的波浪水槽试验,并基于试验结果提出了板式桥梁上部结构所受波浪荷载的计算公式。同时,美国国有公路运输管理协会AASHTO基于大量桥梁上部结构波浪荷载的水槽试验与理论分析结果,提出了板式和T梁上部结构桥梁的准静态及冲击波浪荷载理论模型,用以指导极端波浪作用下跨海桥梁上部结构的设计和改造修复工作[13]。Guo等[14]通过在波浪水槽中开展1∶10的缩尺试验研究了波浪参数和淹没深度对T梁上部结构所受极端波浪荷载的影响,研究指出当上部结构处于静水面附近位置时,结构所受竖向极端波浪荷载的冲击力成分不容忽略,其数值最大时可与准静态力持平。随着计算机技术和计算流体动力学(computational fluid dynamics,CFD)的发展,国内外学者采用数值仿真的方法进一步丰富了桥梁上部结构极端波浪荷载方面的研究。从波浪类型、淹没深度、桥面开孔、波浪参数以及波流耦合等方面研究了影响跨海桥梁T梁上部结构极端波浪荷载的关键因素,并对其影响规律进行了分析和探讨[15-18]。近年来,我国跨海桥梁建设的大规模兴起也促使了国内外研究学者将关注点更多的投向箱形桥梁上部结构,相关水槽试验以及数值仿真研究也随之展开,研究结果表明:上部结构形式的差异导致箱梁与T梁所受波浪荷载有较大差异,箱形桥梁上部结构所受波浪荷载的冲击力成分更多出现在水平方向的荷载上,并且其所承受的竖向荷载要大于同尺寸T梁上部结构,导致现今适用于T梁上部结构的极端波浪荷载计算公式与减灾措施已不再适用于跨海箱形梁桥[19-20]。

值得注意的是,上述桥梁上部结构极端波浪荷载的研究均进行了结构刚性假定,即忽略极端波浪作用下桥梁上部结构的变形与位移以达到节约试验与计算成本的目的。但实际桥梁上部结构与极端波浪的相互作用过程中,存在着桥梁结构位移与波浪场相互影响的复杂耦合现象,刚性结构假定无法真实地反映波浪与桥梁的实际耦合作用过程。同时,通过开展1∶5的波浪与T梁上部结构的大尺度耦合试验与仿真研究,Istrati[21]和Xu等[22]也指出T梁上部结构所受极端波浪荷载的计算中不应忽视流固耦合作用的影响。Chen等[23]相继采用数值仿真方法开展了考虑流固耦合作用下跨海桥梁极端波浪荷载与动力响应的研究初探,结果表明约束刚度、支座形式以及结构特性对极端波浪荷载与动力响应有显著影响,相关研究方法与成果可为跨海桥梁与极端波浪的耦合特性研究提供借鉴和参考。然而,针对考虑流固耦合作用的跨海箱形桥梁上部结构极端波浪荷载与动力特性的研究仍然较少,亟需深入探究极端波浪特性、结构特性以及约束刚度等参数影响下的跨海桥梁流固耦合特性,为未来跨海箱形桥梁上部结构极端波浪荷载的计算理论以及防灾减灾措施研究提供参考。

鉴于此,文章选取某跨海大桥箱形上部结构为研究对象,采用OpenFOAM开源程序,以弹簧-质量-阻尼系统模拟箱形桥梁上部结构运动体系,构建极端波浪与箱形桥梁上部结构相互作用的多相流耦合模型,并基于波浪与T梁上部结构的耦合试验,对多相流耦合模型进行了准确性验证,随后探讨了波浪参数、结构特性以及约束刚度等参数对箱形桥梁上部结构波浪荷载与动力特性的影响。

1 耦合模型建立与验证

1.1 控制方程与求解方法

在极端波浪与跨海箱形桥梁上部结构的耦合仿真模型建立中,涉及空气与水体的两相流模拟,忽略局部变形的箱梁上部结构运动模拟以及追踪结构运动的动网格技术共三部分内容。本文两相流模拟中假定气液两相流为不可压缩黏性流体,流体流动需满足质量与动量守恒,控制方程为不可压缩流体的Naiver-Stokes方程

(1)

(2)

式中:ρ为流体密度;下标i,j分别为笛卡尔坐标系中的x和y方向;u为流体流速;g为重力加速度;p为压力项;μ为流体动力黏度。本文采用流体体积法(VOF)进行气液两相流的界面捕捉,通过引入表征水体体积的体积分数函数α,当体积分数满足0 <α<1时表征气液两相流交界区域,其所满足的对流方程表示如下

(3)

式中,ur为相对速度。

波浪传播以及与结构相互作用的过程中需要模拟湍流流动,采用SSTk-ω湍流模型对雷诺时均方程(reynolds averaged navier-stokes,RANS)进行闭合,通过计算湍流黏性系数来代替各尺度的湍流脉动。SSTk-ω湍流模型在具有高收敛性的同时,能够保证在求解自由剪切流和边界层湍流问题上的高精度,其表达形式如下所示

(4)

(5)

式中:Гk和Гω分别为湍流动能k和湍流耗散率ω的有效扩散率;Gk和Gω为湍流动能系数;Yk和Yω为耗散项;Dω为交叉扩散项。

根据现有现场调研及研究发现,在极端波浪作用过程下跨海桥梁上部结构易发生落梁破坏,而局部变形破坏鲜有发生[24]。因此,在极端波浪与跨海箱形桥梁上部结构的相互作用研究中,不考虑结构自身弹性变形,采用多自由度刚体运动表征箱形桥梁上部结构的运动形式,结构运动过程中所受波浪力和力矩由下式计算得到

F=∬s(pn+τ)dS

(6)

M=∬s(r×(pn+τ))dS

(7)

式中:τ为剪切力矢量;p为结构表面压强;n为结构表面法向量;r为质心到每个表面中心的矢量。

在结构运动方程求解中,采用Newmark-β逐步积分算法,该方法在具有良好计算精度的同时能够保证较高的计算效率,以质量-弹簧-阻尼系统模拟箱梁上部结构水平运动体系,其运动响应方程可表示为

(8)

在波浪与箱形桥梁上部结构的相互作用过程中,结构边界随时间在不断发生改变,流场区域的网格也需随之运动,本文采用动网格技术来实现。考虑到相较于波浪水槽长度,结构运动位移较小,选择网格拓扑不改变的网格变形方法,依据结构位移通过求解Laplacian扩散方程来更新网格节点位置,并为每个单元引入InverseDistance变量来保证网格变形协调。

OpenFOAM采用有限体积法离散上述偏微分控制方程,通过PIMPLE(PISO-SIMPLE)算法求解非定常不可压缩流动的压力速度耦合问题,采用欠松弛迭代法提高求解稳定性,用半隐式MULES方法求解体积分数对流方程。其中时间导数项采用欧拉法进行离散,梯度项使用高斯线性法,拉普拉斯项使用高斯线性修正法。在流固耦合求解过程中,利用松耦合形式对流体控制方程与结构运动响应方程进行联合求解。

1.2 耦合模型建立

基于流体控制方程与流体体积法构建二维数值波浪水槽,用以模拟极端波浪的生成、传播及冲击作用。依据桥址区实测资料,确定本文研究所涉及极端波浪的波浪要素取值,波高设为2～6 m,假定周期为定值10 s,水深为20 m[25-26],依据线性波浪弥散关系可知对应极端波浪的波长约为120 m。为保证极端波浪的生成与充分发展,数值波浪水槽长设置为800 m,高30 m,如图1所示。采用速度入口造波生成Stokes二阶波浪以实现极端波浪的模拟,设置左侧入口250 m长度的消波区来削弱反射波对入射波浪的影响,结构位于离入射波浪边界300 m位置,在波浪水槽右端设置400 m长度的消波区以消除出口边界波浪反射对于波浪输入不稳定的影响。数值水槽右端采用压力出口边界,结构物表面以及水槽底部采用滑移边界,水槽顶部设置为大气出流边界,允许空气在边界处进出。

图1 耦合模型示意图(m)Fig.1 Sketch of the wave-structure coupling model (m)

依据某跨海桥梁引桥段箱形上部结构设计资料,确定箱梁结构尺寸见图1。通过设置弹簧阻尼单元模拟箱形桥梁上部结构的两端支撑情况,在箱形桥梁上部结构迎浪侧与背浪侧分别设置弹簧约束支座,迎浪侧支座考虑水平与竖向弹簧约束,背浪侧仅考虑竖向弹簧约束。基于跨海桥梁设计资料及以往文献研究,可确定箱梁上部结构质量m= 26 400 kg/m,水平弹簧约束刚度kH通过常见上部结构自振周期计算得到,依据固定阻尼比ξ= 0.05可得结构阻尼c,不考虑结构竖向位移的情况下设置竖向弹簧约束刚度kV为107kN/m。

为保证数值计算的准确性与高效性,以结构波浪荷载与动力响应为基准开展了不同网格划分方案的结果敏感性分析,在兼顾计算效率的基础上确定合适的网格区域划分与网格尺寸。表1给出了不同网格尺寸下的结果敏感性和计算效率分析,测试工况采用2.1节中波高为5 m,结构自振周期为1 s的流固耦合算例。通过调整不同结构近壁面网格尺寸,得到了不同网格数量下该耦合工况的计算耗时、结构水平波浪荷载极值和水平位移极值结果。可以看出,在近壁面网格尺寸加密至0.03 m×0.03 m时,随着网格尺寸的进一步加密,计算结果无明显变化,但计算耗时却增长显著。因此,后续工况在远离结构处采用较为稀疏的网格,波浪以及结构物附近加密以提高波浪、边界层以及流固耦合模拟的准确性。最终所采用网格模型方案如图2所示,设置远离结构处稀疏网格尺寸为1 m×1 m,主要计算区域为0.125 m×0.125 m,结构物近壁面为0.03 m×0.03 m。不同网格尺寸间采用逐渐加密的方式,保证一个波长范围内横向网格数量约为1 000个,波高范围内网格数量约为50个,以及满足近壁面y+值的要求。计算过程中时间步长依据库朗数条件限制进行自适应调整,起始计算时间步长设置为0.001 s,最大库朗数设为0.5。

表1 网格敏感性与计算效率分析Tab.1 Analysis of mesh sensitivity and computational efficiency

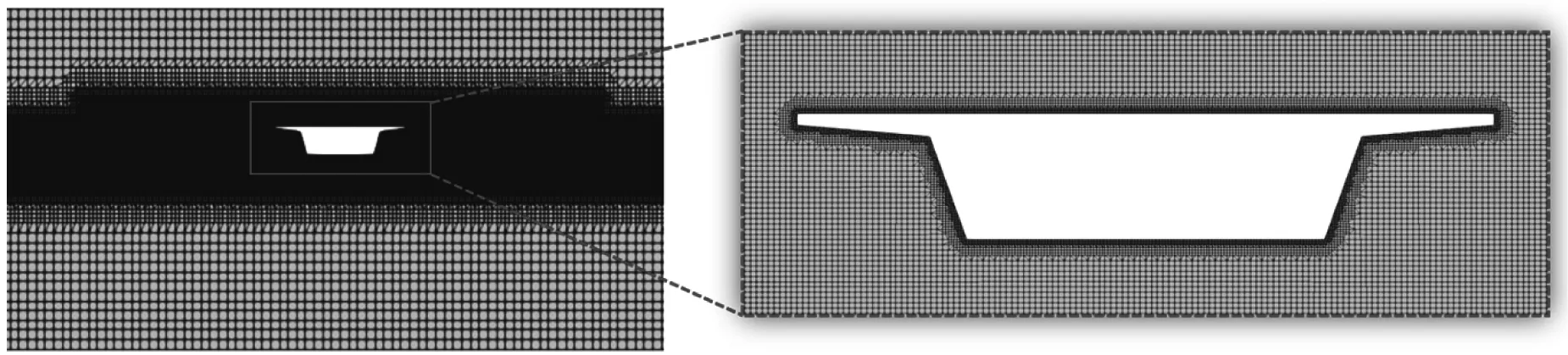
图2 网格划分及加密示意图Fig.2 Schematic diagram of grid division and encryption

1.3 耦合模型验证

本文通过三组理论解、试验结果与仿真模拟的对比分析,验证上述建立的耦合模型在后续极端波浪作用下跨海桥梁箱形上部结构耦合特性问题计算的可靠性。

首先,通过将数值水槽所造极端波浪的波面结果与Stokes二阶波浪的理论解进行对比,验证本文数值波浪水槽的造波准确性。无结构时距入口边界300 m处数值水槽波浪面变化情况与理论解的对比情况如图3所示。其中波浪周期为10 s,水深为20 m,波高分别为3 m和6 m。可以看出,在距入口边界300 m处,除前两个周期的波浪还未发展稳定外,数值水槽所造Stokes二阶波能够保证至少8个周期以上波浪的准确生成与稳定传播,波面变化与Stokes二阶波浪的理论解吻合较好,能够证明本文所建立数值波浪水槽能够准确模拟极端波浪的生成与传播特性。

(a) 3 m波高

由于现有关于箱梁上部结构在极端波浪作用下的耦合试验还未曾开展,现基于Bradner等[27]开展的T梁上部结构与波浪相互作用的试验结果以及Xu等开展的极端波浪作用下T梁受力与动力响应的数值仿真结果,验证本文构建的耦合仿真模型在计算跨海桥梁上部结构极端波浪耦合仿真问题的准确性。Bradner等在俄勒冈大学的大型波浪水槽中开展了比尺为1:5的T梁上部结构波浪荷载与动力响应试验研究,大型波浪水槽长104 m,宽3.66 m及深4.57 m,试验原型选取佛罗里达州Escambia海湾中Katrina飓风中破坏的T形桥梁上部结构。试验中水深为1.89 m,采用波高为0.5 m和周期为2.5 s的规则波浪。同时,通过设置T形桥梁上部结构与盖梁的锚固连接,试验研究规则波浪作用下T型桥梁上部结构刚体所受的波浪荷载情况。试验中通过将主梁水平放置于自制滑轨上,模拟波浪作用下T型桥梁上部结构的水平运动,在滑轨与主梁之间设置刚度为107 kN/m的连接弹簧,模拟下部结构及支座对上约束作用,试验研究考虑波浪-结构相互作用的T型桥梁上部结构波浪荷载及动态响应情况。Xu等采用CFD软件Fluent与动网格更新技术,建立了波浪作用下考虑T形桥梁上部结构水平位移的仿真模型,进行了波浪作用下T型桥梁上部结构的动态响应与波浪荷载参数化分析,研究中Xu等也根据Bradner等设置的试验参数进行了数值仿真计算,其结果亦可用于本文所构建耦合模型的准确性验证。

采用上述构建的OpenFOAM流固耦合模型,基于试验水槽尺寸及试验布置,建立了1∶1数值模型,分别模拟了上部结构为刚体以及考虑上部结构水平运动两种情况下的结构受力情况。所提出模型计算刚性T形桥梁上部结构的波浪荷载与Bradner等试验结果及Xu等数值仿真结果的对比情况如图4所示。可以发现基于本文仿真模型计算得到的T形桥梁上部结构所受水平向Fx和竖向波浪荷载Fy与试验结果吻合较好,能有效模拟T形桥梁上部结构所受波浪荷载的变化情况,表明本文所提出模型在计算规则波浪作用下刚体结构所受波浪荷载上具有较高的准确性。由图5可知,采用耦合模型计算考虑结构水平位移的T形桥梁上部结构波浪荷载与Bradner等试验结果及Xu等数值仿真结果的吻合良好。本文耦合仿真模拟结果中,水平波浪荷载峰值为3 795 N,竖向波浪荷载峰值为16 754 N,而试验结果中T形桥梁上部结构所受水平波浪荷载峰值为3 992 N,竖向波浪荷载峰值为14 472 N,波浪荷载峰值模拟结果比试验值差距了4.9 %和13.6 %,仿真模拟误差在可接受范围内,且相较于Xu等数值仿真结果在结构所受水平波浪荷载峰值的计算上略有优势。表明本文基于OpenFOAM所提出的耦合模型能够准确模拟考虑结构水平位移的波浪-结构相互作用。

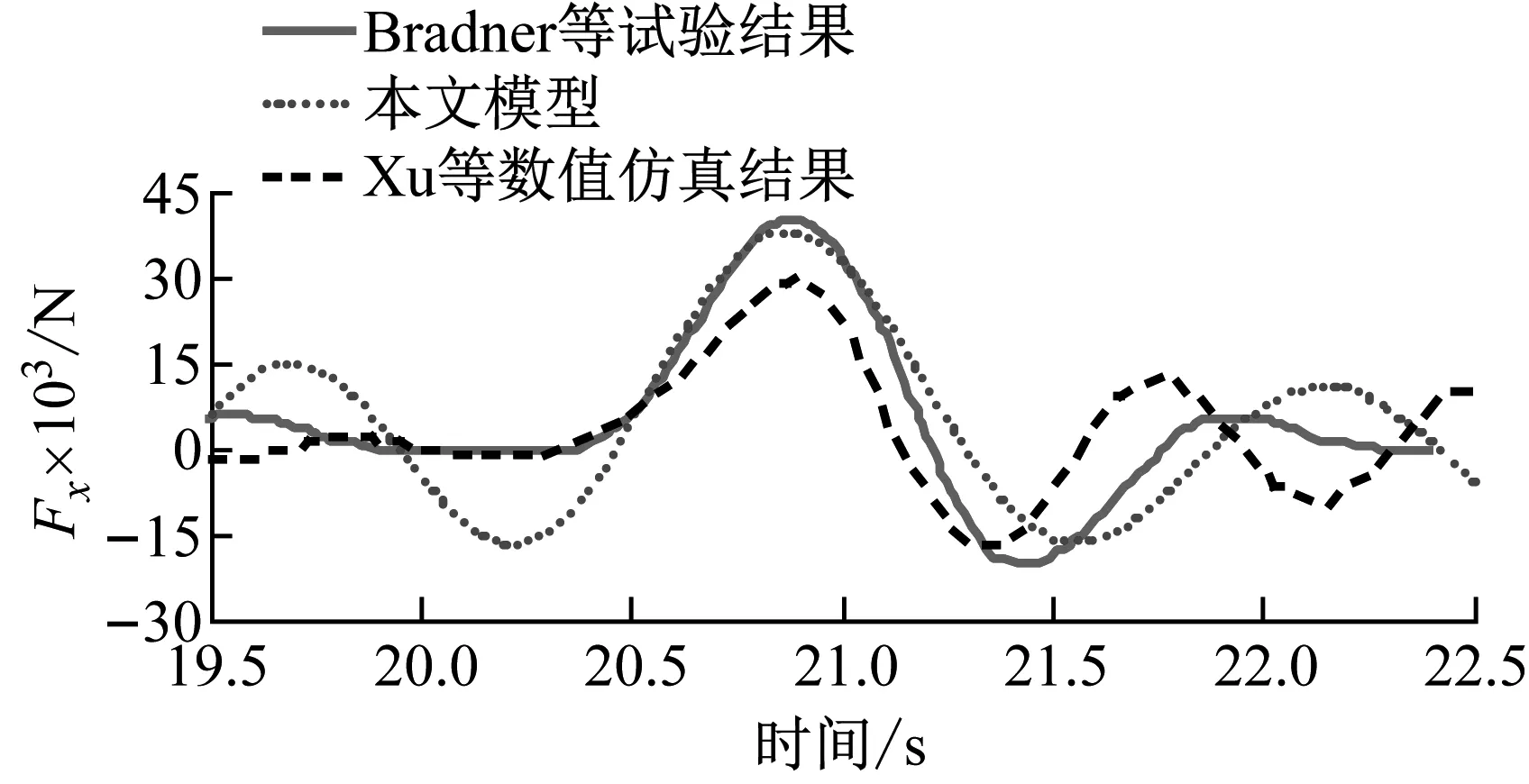
(a) 水平波浪力

2 跨海箱形桥梁上部结构流固耦合特性与参数化分析

在已验证的流固耦合模型基础上,开展结构特性与波浪参数对跨海箱形桥梁上部波浪荷载、结构动力响应及支座力的影响规律研究。首先,将刚性跨海箱形桥梁上部结构所受波浪荷载与考虑结构水平位移时箱形桥梁上部结构所受波浪荷载进行对比,探究波浪-结构相互作用对波浪荷载的影响。继而展开跨海箱形桥梁上部结构动力响应和支座力的参数化分析。依据跨海箱形桥梁上部结构的设计资料和桥址区水文资料,桥址区水深设定为20 m,波浪周期采用固定值T= 10 s,假定箱形桥梁上部结构处于将要淹没的最不利状态,即结构底面与水面齐平。考虑五组波高H= 2,3,4,5,6 m以及不同结构特性TS= 0.6-2.0 s对跨海箱形桥梁上部结构动力响应与所受波浪荷载的影响,依据结构自振周期、阻尼与水平刚度的关系计算所得弹簧-质量-阻尼体系的特性参数如图6所示。

图6 弹簧-质量-阻尼体系的特性参数Fig.6 Characteristic parameters of the spring-mass-damping system

2.1 流固耦合对结构波浪荷载的影响

本节主要研究流固耦合效应对箱形桥梁上部结构所受波浪荷载的影响。主要针对入射波高为5 m的工况。刚性跨海箱形桥梁上部结构所受波浪荷载与考虑流固耦合时箱形桥梁上部结构所受波浪荷载的对比如图7所示。刚性箱形桥梁上部结构所受波浪荷载与考虑流固耦合时的波浪荷载时程曲线较为相似。但由于弹簧支座的缓冲消能以及结构与周围水体的相互作用,考虑结构水平位移后结构所受波浪荷载的波动明显增强,同时波浪荷载极值也有所下降。在波浪与结构相互作用过程中,波浪开始作用在箱形桥梁上部结构上时,波浪力由于波浪冲击作用迅速上升达最大值,但结构产生位移后,弹簧约束力与周围水体对结构位移的影响导致其最大值相较于刚性跨海箱形桥梁上部结构所受波浪荷载有所下降,同时结构与流体的耦合效应加剧了箱形桥梁上部结构所受波浪荷载的波动性。

(a) 水平波浪力

由图8可知,跨海箱形桥梁上部结构所受波浪荷载的极值随着结构自振周期的增加呈现下降的趋势。相较于刚性跨海箱形桥梁上部结构所受波浪荷载极值(图8中Ts= 0的工况),考虑流固耦合时结构所受波浪荷载极值下降幅度明显,其中水平波浪力最大降低28 %,竖向波浪力最大降低22.5 %。表明不考虑流固耦合效应下的跨海箱形桥梁上部结构所受波浪荷载计算会过高估计实际受力,导致结构设计过于保守,造成资源浪费。

(a) 水平波浪力

2.2 箱形桥梁上部结构动力响应

本节主要研究结构特性及波高参数对箱形桥梁上部结构动力响应的影响。图9为波高为5 m时,不同结构自振周期下箱形桥梁上部结构的水平位移时程曲线。随着结构自振周期的增大,箱形桥梁上部结构所受的水平弹簧约束刚度呈现下降的趋势,进而极端波浪作用下箱形桥梁上部结构的水平位移呈现增大的趋势。结合图7中箱形桥梁上部结构所受波浪荷载可知,波浪冲击作用于箱形桥梁上部结构后,结构所受波浪荷载逐渐增大并且伴随着结构的正向水平移动。由图7可知,不同水平弹簧约束刚度下结构所受波浪荷载达到极值的时刻基本一致,然而箱形桥梁上部结构水平位移峰值的出现时刻有较大差别。结合波浪荷载极值与水平位移极值出现时刻,可以发现波浪在冲击作用于结构时,波浪荷载迅速达到极值,此时在弹簧水平约束下结构水平位移较小。随着水平弹簧约束刚度的下降,结构水平位移增大,导致结构与水体的相互作用加剧,结构所受波浪荷载极值降低。随后在波浪的冲击与水平弹簧约束的作用下,箱形桥梁上部结构首先产生正向水平位移,与水体的相互作用以及约束力的增加均导致了波浪荷载的减小。继而在约束力与波浪力共同作用下,上部结构向波浪传播反方向运动。当上部结构恢复至其初始位置后,弹簧约束力减小至零,而波浪作用产生的水平波浪力始终沿着波浪传播方向,上部结构又开始沿波浪传播方向运动直至位移最大处,此时结构所受的反向水平波浪力达到极值。由此可见,极端波浪作用下箱形桥梁上部结构结构与水体间会发生复杂的相互作用,且水平约束刚度对结构响应有较大影响。

图9 结构自振周期对箱形桥梁上部结构水平位移时程的影响Fig.9 Influence of natural vibration period on the time history of horizontal displacements of box-girder superstructure

采用小波变换方法进行箱形桥梁上部结构动力响应时程的分析如图10所示,此时入射波高为5 m。可以发现极端波浪作用下箱形桥梁上部结构的水平位移主要受到入射波浪参数特征以及结构自身特性的影响,其中小于0.4 Hz的低频部分主要是由于入射波浪引起的,因为不同结构振动特性下该低频部分始终存在,并且约束刚度的减小会加剧入射波浪特性对结构响应的影响。高频部分主要与结构自振周期相关,其主要频率基本与结构自振周期一致。并且随着结构自振周期的增大,约束刚度的减弱会导致极端波浪作用下箱形桥梁上部结构与高频部分相关的水平响应持时的增加,而在结构自振周期较小时,较强的水平约束会较快地使结构进入平衡稳定状态。

(a) 结构自振特性 Ts = 0.6 s

图11给出了入射波高为5 m以及结构自振周期为2.0 s时跨海箱形桥梁上部结构与极端波浪的作用过程。结合图7可知在43 s时,波浪前锋冲击作用于箱形桥梁上部结构的腹板处,导致此时箱形桥梁上部结构所受波浪荷载达到峰值,但此时由于冲击作用时间较短,结构水平位移较小。在44 s时波峰继续传播作用于结构,此时结构水平位移达到正向峰值。随着波浪的继续传播,在弹簧约束的作用与波浪水质点的带动下,箱形桥梁上部结构向波浪传播的反方向运动,并在45 s时到达最大负向位置处。随后箱形桥梁上部结构继续沿着波浪传播方向运动,约束力逐渐减小至零,箱形桥梁上部结构正向水平位移在46 s再次达到峰值,此时结构所受负向水平波浪荷载亦达到极值。可以发现,跨海箱形桥梁上部结构与极端波浪的作用过程中结构响应与波浪荷载具有较为显著的关联。

(a) 43 s

不同结构振动周期下箱形桥梁上部结构的水平位移极值随波高的变化情况见图12。当入射波浪的波高较小时,且当结构振动周期Ts≤ 1.0 s时,波高对箱形桥梁上部结构水平位移极值的影响较小。然而当结构振动周期大于1.0 s时,随着结构振动周期的增大,波高对箱形桥梁上部结构水平位移极值的影响急剧上升。在波高为6 m和结构振动周期为2.0 s时,箱形桥梁上部结构的水平位移极值可达480 mm,该水平位移已经远超箱形桥梁上部结构允许位移。因此,在箱形桥梁上部结构设计中,通过降低结构振动周期来降低箱形桥梁上部结构所受极端波浪荷载的同时,应考虑约束刚度降低而造成的结构水平位移增大的影响。

图12 不同结构振动周期下水平位移极值随波高的变化Fig.12 Variation of maximum horizontal displacements of the box-girder superstructure with the wave height under different natural vibration periods

2.3 支座水平力

图13给出了波高为5 m,结构自振周期为2.0 s时,箱形桥梁上部结构所受水平波浪力与迎浪侧支座水平力的对比情况。由图可知,支座水平力要比结构所受水平波浪荷载稍显滞后,这是由于在波浪冲击作用于箱形桥梁上部结构的初始阶段,波浪荷载会在短时间内达到峰值,但此时结构响应较小,导致荷载尚未完全传递至支座处。随着箱形桥梁上部结构水平位移的增大,支座约束的增大会带来支座水平力的增加,随着结构与波浪的相互作用,支座水平力会产生上下波动,箱形桥梁上部结构在支座拉压力与波浪的共同作用下水平移动直至达到稳定。值得注意的是,支座所受水平力较箱形桥梁上部结构所受水平波浪力约大17 %,主要原因是支座不仅承受了由上部结构所传递下来的水平波浪力,同时还需要承受结构运动所产生的惯性力。因此,在跨海桥梁上部结构的支座设计中仅依据上部结构所受波浪荷载是不准确的,应考虑结构运动及流固耦合效应对支座力的影响。

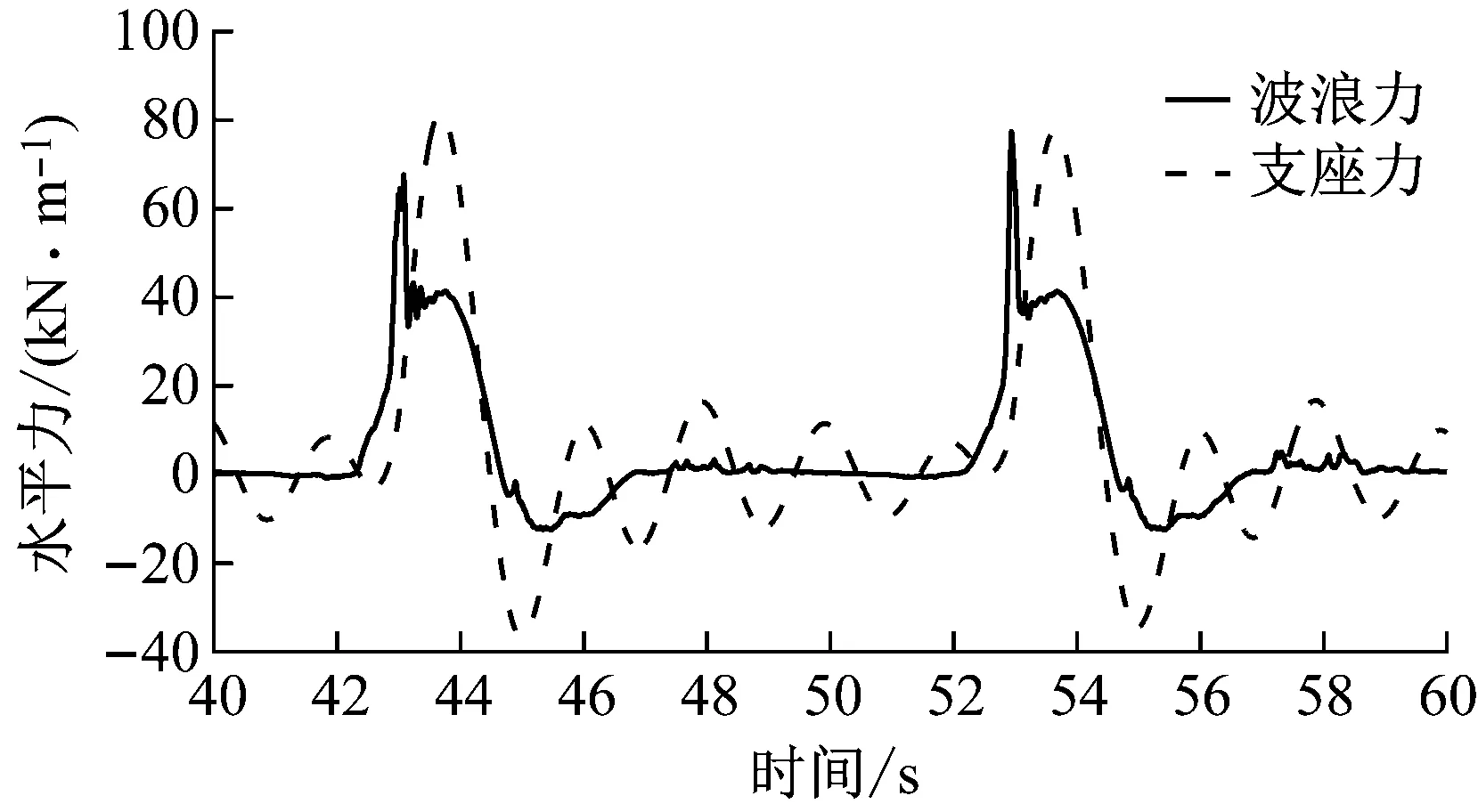
图13 箱形桥梁上部结构水平波浪力与迎浪侧支座水平力的对比Fig.13 Comparison of the wave force of the box girder superstructure and the horizontal support reaction of the wave side support

由图14可知,不同结构振动周期下迎浪侧水平支座力极值随波高的变化也有所差异。随着波高的增大,水平支座力呈现增加的趋势,而随着结构自振周期的增大,水平支座力呈现下降的趋势,该现象与箱形桥梁上部结构所受波浪荷载随结构自振周期的变化趋势相同。以波高为5 m为例,结构自振周期为0.6 s的箱形桥梁上部结构的支座力较其所受水平波浪力大54.9 kN/m,而结构自振周期为2.0 s的箱形桥梁上部结构的支座力较其所受水平波浪力仅大15.3 kN/m,即结构自振周期的增大能有效降低箱形桥梁上部结构的支座水平力。主要原因是随着结构自振周期的增大,约束刚度的减小,箱形桥梁上部结构在与波浪相互作用中水平位移的增加导致了更多的能量耗散,带来了支座水平力的减小。因此,结合箱形桥梁上部结构的水平位移限制,选择合适的约束刚度能够有效降低箱形桥梁上部结构所受波浪荷载与支座荷载,提升极端波浪作用下跨海箱形桥梁上部结构的安全性。

图14 不同结构振动周期下迎浪侧水平支座力极值随波高的变化Fig.14 Variation of maximum horizontal support reactions of the wave side support with the wave height under different natural vibration periods