基于O-U特征的Bachelier模型的期权定价
2023-09-19钱维佳陈海枫陈安钢吕照进奚雷
钱维佳 陈海枫 陈安钢 吕照进 奚雷
摘 要:随着“负油价”现象的出现,对于期权等衍生产品来说,标的资产负价格意味着经典Black-Scholes模型失效。本文对原始的Bachelier模型进行修改,保留标的资产价格可以为负的特点,并且使其具有Ornstein-Uhlenbeck随机过程特征。基于修正的Bachelier模型结合蒙特卡洛数值算法对欧式期权、美式期权以及障碍期权进行定价,进一步扩展其期权定价应用范围。通过数值模拟,基于修正的Bachelier模型在期权定价上表现出很高的计算精度,基于O-U特征的Bachelier模型的期权定价可以作为Black-Scholes模型期权定价的替代方案,指导期权等衍生品定价决策。
关键词:Black-Scholes模型;Bachelier模型;期权定价;障碍期权;负标的资产
一、引言
2020年4月20日,西得克萨斯中质原油(WTI)5月期货价格暴跌305%,至每桶-3673美元,这是芝加哥商品交易所(CME)历史上该大宗商品首次出现负价格,天然气等其他大宗商品的价格此前曾跌至0美元以下。在价格跌入负值的情况下,买家将获得提货报酬,但是由于运输和储存等相关成本的原因,致使有超过79万手的多头被迫与票据交易所进行现金结算。WTI是一种特定等级的原油,是石油定价的三大基准之一,其出现负油价在国际金融市场引发了连锁反应:抄底原油的多头纷纷爆仓,损失惨重;产油国及原油公司面对低油价和原油供给过剩致使仓储和财务崩溃,面临着巨大的经济风险。
负油价的出现主要有以下四个原因:第一,根据国际能源署的数据,由于新冠疫情迫使世界各国发布“居家隔离”政策,以减缓疾病的传播,致使原油需求预计将减少2900万桶/天,经济活动减少意味着对原油及其副产品(包括汽油和航空燃料)的需求减弱。第二,供需矛盾激化原油仓储运输成本直线飙升,期货多头行权交割时,必须承担原油的运输、储存等巨额成本,最终导致多头不得不以现金方式与交易所平仓。第三,芝加哥商品交易所清算所(CME Clearing)公布测试以支持潜在的负油价期权的可能性,并使市场继续正常运作,允许出现负油价的机制致使石油市场引发极端混乱。第四,负油价危机暴露了金融交易监管和风险管理方面的不足之处,金融机构存在交易规则、风险管控、衍生产品设计、投资者教育宣传等诸多不规范,美国商品期货交易委员会后来发布建议,希望金融机构持续做好应对某些合约的极端市场风险。
负油价的冲击之后,芝加哥商品交易所和ICE
于當月做出决定,立即改用Bachelier模型进行期权定价,正式开启允许标的资产价格为负的交易情形。①此次CME正是利用Bachelier模型中标的资产价格可以为负的特点为原油期货期权进行定价,以维持结算的正常进行。对于期权等衍生产品来说,标的资产负价格意味着经典Black-Scholes模型失效,使得Bachelier期权定价模型再度被应用。但即使没有负油价,也有充分的理由考虑使用Bachelier期权定价模型。其一,Bachelier模型是第一个分析布朗运动(BM)数学特性,为股票价格变化的随机过程建模的模型,比Black-Scholes模型早了70多年。Bachelier期权定价模型在为某些合约定价方面,会比Black-Scholes模型(防止标的资产价格路径为负)有一些优势。例如,Bachelier波动微笑曲线比Black-Scholes曲线更适合石油市场。其二,在固定收益市场,由于对数正态分布不能准确地描述利率变化的随机过程,Bachelier模型已经被广泛使用在利率等衍生产品上。例如,掉期是由Bachelier波动率报价和风险管理的。即使负油价是市场变化的一次突发事件,从风险管理角度,将Bachelier模型纳入定价系统也会对金融衍生品定价起到指导决策作用。
中国证券期货2023年8月
第4期基于O-U特征的Bachelier模型的期权定价
尽管负油价的出现使很多学者开始重新研究Bachelier模型,仍然很难找到关于该模型的全面应用,主要由于Bachelier模型存在着标的资产可能为负等缺点,一直没有得到很广泛的应用。本文对最原始的Bachelier模型做了相应修改,保留其标的资产可以为负的特性,同时增加资金的时间价值和标的资产均值回复的特性,使其具有Ornstein-Uhlenbeck随机过程特性,并基于修正的Bachelier模型结合蒙特卡洛等数值算法为更多种类的期权定价。在实证分析中,基于修正的Bachelier模型对欧式期权(涉及正负标的资产价格)、美式期权以及障碍期权进行定价,对于期权定价有着非常好的参考指导价值,尤其在负标的资产的期权定价上。
二、期权模型与期权定价
本节主要介绍常见的期权定价模型,并对每行模型进行随机过程求解和标的资产价格分布与价格路径模拟。同时基于常见的两个期权模型进行期权定价,最后介绍两种常用的期权定价数值算法,并基于两种数值算法扩展对Bachelier模型的应用范围,使其可以被运用到欧式期权、美式期权和障碍期权。
(一)期权模型
Displaced Black-Scholes模型是具有一般性的标的资产价格随机模型,其模型结构如式(1)所示,此模型基本涵盖了金融标的资产价格变化的各种随机过程,如β=1,标的资产价格随机过程为Black-Scholes模型,常用于金融衍生产品的定价建模;β=0,标的资产价格随机过程为Ornstein-Uhlenbeck模型,常用于刻画利率、大宗商品价格等建模;β=1,σ也是随机过程,此模型为随机波动率模型,即Heston模型。
dS(t)=(r-q)S(t)dt+σ[βS(t)+(1-β)]dW(t)(1)
其中,S(t)表示标的资产在初始时刻t的价格,r表示市场无风险利率,q表示净便利收益率或红利率,σ表示标的资产价格的瞬时波动率或绝对波动率,β表示模型可调系数,W(t)为标准布朗运动。
通过求解,其标的资产在t时刻的价格如式(2)所示:
S(t) =S(0)e(r-q-12σ2β2)t+∫t0σβdW(s)-∫t0σ2β(1-β)e(r-q-12σ2β2)s+∫s0σβdW(s)ds+∫t0σ(1-β)e(r-q-12σ2β2)s+∫s0σβdW(s)dW(s)(2)
1Black-Scholes模型
Black-Scholes模型是第一个被广泛使用的计算期权合约理论价值的数学方法,该方法是基于其标的资产估算衍生品的理论价值,同时考虑时间价值和其他风险因素的影响。由于Black-Scholes模型严苛的模型假设,使期权定价结果往往偏离实际交易市场价格,同时标准Black-Scholes
① CME Group,Switch to Bachelier Options Pricing Model-Effective April 22,2020Advisory Notice #20-171CME
CME Group,2020bValuation Model Change for Four Natural Gas Option Products-Effective May 26,2020Advisory Notice #20-209,CME
模型仅适用于欧式期权定价,因此在期权定价方面出现了许多修正的Black-Scholes定价模型,使Black-Scholes模型进一步得到广泛应用。如式(1)所示,当β=1,标的资产价格的随机过程为Black-Scholes模型,在风险中性测度下标的资产价格变化过程符合几何布朗运动,其模型结构如式(3)所示:
dS(t)=(r-q)S(t)dt+σS(t)dW(t)(3)
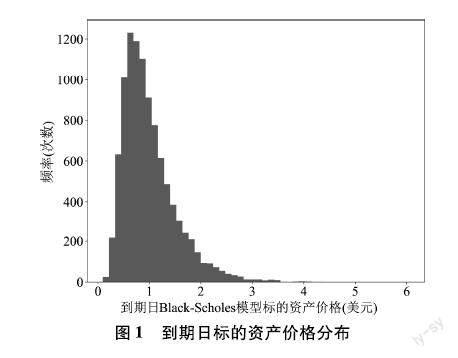
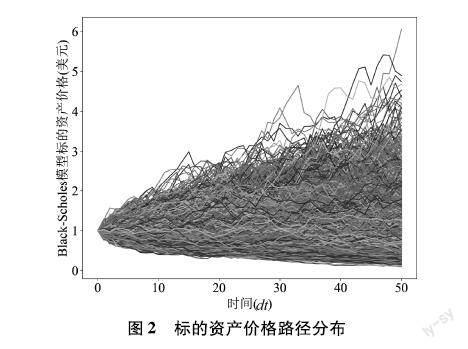
基于Black-Scholes模型的标的资产到期日价格分布和标的资产价格路径分布如图1和图2所示,Black-Scholes模型的标的资产价格呈现对数正态分布形式且价格总是大于0。
图1 到期日标的资产价格分布
图2 标的资产价格路径分布
根据式(2),Black-Scholes模型下的标的资产在T时刻的价格S(T)如式(4)所示:
S(T)=S(t)expr-q-12σ2
(T-t)+σT-t·z(4)
在该模型假设下,基于等价鞅测度法进行风险中性定价:假设在初始时刻t,标的资产初始价格为S(t)、T为期权到期日、K为期权执行价格。欧式看涨期权价格等于其未来到期时的payoff的期望值的贴现如式(5)所示:
VCBS=e-r(T-t)(ST-K)+=e-r(T-t)S(t)expr-q-12σ2
(T-t)+σT-t·z-K+=S(t)ΦlogS(t)K+12σ2(T-t)σT-t- Ke-r(T-t)ΦlogS(t)K-12σ2(T-t)σT-t
(5)
其中,Φ(·)为标准正态分布的累积分布函数,相应的欧式看跌期权价格可以由期权的平价公式推导得出。
2具有O-U特征的Bachelier模型
经典的Bachelier模型刻画的是t时刻期货价格随机过程:dF(t)=σdW(t)。本文在此模型上进行修改,使修正的Bachelier模型具有均值回复的Ornstein-Uhlenbeck随机过程,即式(1)的标的资产价格随机过程,在β=0时为具有均值回复的Bachelier模型,其模型结构如式(6)所示:
dS(t)=(r-q)S(t)dt+σdW(t)(6)
基于修正的Bachelier模型式(6),带入F(t)=e(T-t)(r-q)S(t),可以得出t时刻期货价格随机过程如式(7)所示:
dF(t)=e(T-t)(r-q)σdW(t)(7)
与经典的Bachelier模型相比,两种模型的主要区别是波动率呈指数增长或指数下降,但修正的Bachelier模型保留了Bachelier模型的特点,同时加入了O-U过程的均值回复的特征。
根据式(2),修正的Bachelier模型下的標的资产在T时刻的价格S(T)如式(8)所示:
S(T)=S(t)e(r-q)(T-t)+σe2(r-q)(T-t)-12(r-q)·z(8)
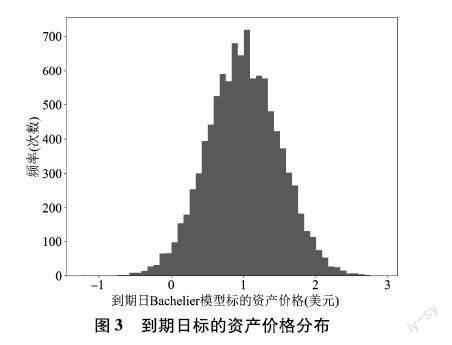
基于修正的Bachelier模型的标的资产到期日价格分布和标的资产价格路径分布如图3和图4所示,Bachelier模型的标的资产价格分布呈现正态分布形式,同时存在负价格情形。
图3 到期日标的资产价格分布
图4 标的资产价格路径分布
与Black-Scholes模型一样的条件下,基于等价鞅测度法进行风险中性定价,欧式看涨期权价格如式(9)、式(10)所示,其中f(z*)和N(z*)是标准正态分布的概率密度函数和累积分布函数,相应的欧式看跌期权价格可以由期权的看涨-看跌平价公式推导出。
VCBL=e-r(T-t)[(ST-K)+]=e-r(T-t)S(t)e(r-q)(T-t)+σe2(r-q)(T-t)-12(r-q)z-K+=e-r(T-t)∫z*(S(t)e(r-q)(T-t)+σe2(r-q)(T-t)-12(r-q)z-K)f(z)dz=e-r(T-t)(S(t)e(r-q)(T-t)-K)∫
SymboleB@
z*σe2(r-q)(T-t)-12(r-q)zf(z)dz=e-r(T-t)(S(t)e(r-q)(T-t)-K)N(z*)+σe2(r-q)(T-t)-12(r-q)∫
SymboleB@
z*zf(z)dz=e-r(T-t)(S(t)e(r-q)(T-t)-K)N(z*)+σe2(r-q)(T-t)-12(r-q)∫
z*ze-z222πdz=e-r(T-t)(S(t)e(r-q)(T-t)-K)N(z*)+σe2(r-q)(T-t)-12(r-q)f(z*)(9)
S(t)e(r-q)(T-t)+σe2(r-q)(T-t)-12(r-q)z*-K>0z*=S(t)e(r-q)(T-t)-Kσe2(r-q)(T-t)-12(r-q) (10)
(二)期权定价数值算法
1二叉树法
二叉树期权定价模型(二叉树模型)是1979年发展起来的一种多周期期权估值方法,在期权起始日和到期日之间指定时间步长,二叉树期权定价模型采用迭代方法对期权进行定价,每次迭代假设标的资产价格有两种可能的结果:沿着二叉树向上或向下移动,并且每个时期都使用相同的上涨和下跌概率。如果时间区间被无限细分,二叉树的标的资产价格变动可以收敛到一个几何布朗运动。二叉树期权定价过程可以可视化资产价格在每一期的变化,如美式期权可以根据不同时间点的资产价格来决策评估期权。二叉树期权定价模型构造步骤如下(以单步二叉树为例):
(1)根据标的资产价格波动率σ:计算标的上涨倍数u=eσΔt,下跌倍数d=e-σΔt。
(2)二叉树在Δ时间区间上,标的资产向上运动的收益率为u-1的概率为p,1-p为标的资产向下运动收益率d-1的概率,即风险中性概率p=(erΔt-d)/(u-d)。
(3)欧式期权定价策略:从二叉树的末尾迭代出发,从后往前不断迭代到二叉树的起始点。例如,由q节点的上升和下降时的期权价值(fu和fd)加权平均并且贴现到当前节点,得到当前期权价格:f=e-(r-q)Δt(pfu+(1-p)fd)。
(4)美式期权定价策略:从二叉树的末尾迭代出发,从后往前不断迭代到二叉树的起始点,并且在每个节点上求取最大回报收益:
max[f=e-rT(pfu+(1-p)fd),提前行使期权的收益]。
与Black-Scholes模型相比,二叉树期权定价模型在数学上很简单,而且基于迭代操作,交易者可以提前确定何时可能发生执行决策,增加套利策略的机会。二叉树期权定价模型的缺陷就是每一次迭代其标的资产的价格只能变化两个值,在实际中是不合理的。
2蒙特卡洛算法
蒙特卡洛期权定价算法(蒙特卡洛算法)是基于风险中性定价理论的随机抽样算法,用于计算具有多种不确定性和随机特征的期权价格,如利率、股价或汇率的变化等。利用随机抽样算法模拟标的资产价格运动路径分布,在抽样路径上计算期权在终点的价值,经过多次抽样,将获得的所有收益求均值,然后利用无风险利率贴现后,计算在初始时刻的期权价值。其中,对偶变量法是提高蒙特卡洛,算法模拟精度的一种方法,美式期权定价是基于最小二乘蒙特卡洛算法在每个时点上需要做一次线性回归,从而计算出最优的行权时点,得出期权价格。蒙特卡洛期权定价算法步骤如下:
(1)基于风险中性定价理论的随机抽样算法,模拟标的资产价格St运动路径分布,0≤t≤T。
(2)计算出标的资产价格St每条运动路径的到期回报:max(S(T)-K,0),并结合风险中性定价理论的无风险利率r计算出到期回报的贴现值:CT=e-r(T-t)max(S(T)-K,0)。
(3)不断迭代m次步骤(1)、(2),计算到期回报均值:CMC=1m∑CT=1me-r(T-t)∑max(S(T)-K,0),进而得到期权价格的Monte-Carlo模拟值。
三、实证分析
本节利用Black-Scholes模型、二叉树模型、蒙特卡洛期权定价算法和基于Bachelier模型的期权算法分别对欧式期权、美式期权和障碍期权进行定价,通过数值结果的比较分析,说明基于Bachelier模型的期权算法不仅可以应用在标的资产价格为负的期权定价上,还可以应用在美式期权和障碍期权定价上,为期权定价提供一种有效的定价算法。
(一)欧式期权定价
欧式期权规定期权合约持有人只能在到期日行使其权利,期权持有人的权利包括以指定的执行价格购买标的资产或出售标的资产。
1标的资产价格为正的欧式期权定价
首先对标的资产价格为正的欧式期权定价,在不同波动率下,计算不同定价算法对期权的定价结果,期权合约涉及参数:S0=95为标的资产初始价格,K=100为期权行权价格,T=1为期权有效期,r=002为市场无风险收益率,q=001為标的资产的净便利收益率或红利率,σ=02、03、05为标的资产价格不同的波动率。
欧式期权定价算法对比:采用存在解析解Black-Scholes模型算法(BS)、时间步长为200步的二叉树模型(Binarytree)、模拟次数为10000次以及时间步长为200步的Black-Scholes模型的蒙特卡洛算法(BSMC)、基于Bachelier模型的期权定价算法(Bachelier),以及基于Bachelier模型的蒙特卡洛算法(BachelierMC)和对偶变量法蒙特卡洛算法(BachelierDMC)进行数值仿真对比。
从表1数值结果可以看出,利用上述期权定价算法的期权价格结果相似,对期权定价有一定的指导意义。Bachelier模型和Black-Scholes模型的差异主要表现在其标的资产价格所对应的分布不同,当标的资产初始价格S0越小,波动率σ越大时,其分布越容易出现负标的资产价格的情形,从数值结果也可以得出,当波动率σ越大时,Bachelier模型产生的期权价格与基于Black-Scholes模型的解析解的精度误差扩大。精度误差减小可以通过基于Bachelier模型的数值算法的时间步长和模拟次数来提高,当时间步长和模拟次数更加精细时,基于Bachelier模型的期权定价方法的结果将更加贴近Black-Scholes模型的解析解。
2标的资产价格为负的欧式期权定价
美国的WTI原油5月合约暴跌为负值,使得期权等衍生品定价必须面对标的资产为负价格的情形,这里还是采用上一节的参数:T=1,r=002,σ=02、03、05,q=001,仅对标的资产价格和执行价做出修改:S0=-30,K=30。由于Black-Scholes模型为对数正态模型,不合适标的资产价格为负的欧式期权定价,这里采用的算法为时间步长为200步的二叉树模型(Binarytree)、基于Bachelier模型的期权定价算法(Bachelier),以及基于Bachelier模型的蒙特卡洛算法(BachelierMC)和对偶变量法蒙特卡洛算法(BachelierDMC)进行数值仿真对比。
从表2数值结果可以看出,上述期权定价算法对于标的资产为负价格情形下的定价十分精确,对于看涨期权多头,面对标的资产价格暴跌为负时,而在到期日有权利以正的执行价购买期权标的资产,显然多头是拒绝行权,即此时期权价格为0,但是波动率σ较大时,相应的资产波动更加敏感,Bachelier模型定价显示即使标的资产价格出现负值也存在相应的期权价格。对于看跌期权多头,面对标的资产价格暴跌为负时,在到期日有权利以正的执行价出售期权标的资产,多头显然是必须行使此份期权,即此时期权价格为正。
(二)美式期权定价
美式期权允许期权持有人在预定的到期日或之前,根据期权是看涨期权还是看跌期权,以设定的执行价格买进或卖出标的资产。由于投资者可以在合约有效期内的任何时候自由行使期权,所以美式期权比欧式期权更有价值。
这一节还是采用上两节的参数进行期权算法对比模拟,正标的美式期权定价的参数与第一节参数一致,负标的美式期权定价的参数与第二节参数一致。本节只验证美式看跌期权定价算法对比,美式看涨期权可以通过期权平价关系求解,采用的算法为时间步长为200步的二叉树模型(Binarytree)、基于Black-Scholes模型的最小二乘蒙特卡洛期权定价算法(BSLMC),以及基于Bachelier模型的最小二乘蒙特卡洛期权定价算法(BachelierLMC)进行数值方法对比,其中Black-Scholes模型期权定价算法(BS)和Bachelier模型的期权定价算法(Bachelier)为欧式看跌期权定价结果。
从表3数值结果可以看出,不管标的资产价格为正或负,三种期权定价算法精度都很精确,由于涉及净便利收益率或红利率的美式期权到期日前都是可以随时行权,也验证了其美式看跌期权的价格都大于欧式看跌期权价格。
(三)单障碍期权定价
障碍期权是一种路径依赖的场外奇异期权衍生品,其收益根据障碍期权的标的资产是否达到或超过期权合同中规定的预定价格,如果标的资产的价格超过一定的障碍值而使期权合约失效,此时为敲出失效期权;反之为敲入生效期权。障碍期权的优点就是相对欧式期权或美式期权,其期权价格低廉。本文主要考虑的单障碍期权,可以分为向上敲出失效看涨期权(UOC)、向上敲入生效看涨期权(UIC)、向上敲出失效看跌期权(UOP)、向上敲入生效看跌期权(UIP)、向下敲出失效看涨期权(DOC)、向下敲入生效看涨期权(DIC)、向下敲出失效看跌期权(DOP)、向下敲入生效看跌期权(DIP)。
障碍期权只要期权有效期内有效,其收益和欧式期权相似,一份普通欧式看涨期权价格如式(11)所示,N为标的价格随机路径数,Sj,T为标的到期日价格,K为期权执行价,P(Sj,T)为对应标的价格概率。
VEuropean= e-r(T-t)∑Nj=1[max(Sj,T-K,0)×P(Sj,T)]
(11)
一份向上敲出失效看涨期权(UOC)价格如式(12)所示,n为标的价格触碰障碍值的路径数,Sj,t≤i≤T为期权有效期内的标的价格,K为期权执行价,P(Sj,t≤i≤T VBarrier= e-r(T-t)∑N-nj=1[max(Sj,T-K,0)×P(Sj,t≤i≤T 本节主要给出8种不同的单障碍期权定价对比,在不同波动率下,计算不同定价算法对期权的定价结果,其中向上敲出敲入期权选取参数为S0=95,K=100,T=1,r=002,σ=02、03、05,q=001,障碍值L=105;向下敲出敲入期权选取参数为S0=95,K=100,T=1,r=002,σ=02、03、05,q=001,障碍值L=90。采用的期权定价算法为单障碍期权解析解(Analytic solution)、基于Black-Scholes模型的蒙特卡洛期权定价算法(BSMC),以及基于Bachelier模型的蒙特卡洛期权定价算法(BachelierMC)进行数值方法对比,其中蒙特卡洛模拟次数为10000次,时间步长为200步。 表4至表5数值基于Black-Scholes模型的蒙特卡洛期权定价算法(BSMC)以及基于Bachelier模型的蒙特卡洛期权定价算法(BachelierMC)都与障碍期权解析解在定价结果上很接近,可以通过调节蒙特卡洛模拟次数和时间步长达到更精确结果。通过以上内容可以看出,障碍期权的价格不仅与障碍值有关,也与波动率水平密切相关,当障碍值固定时,波动率水平越大,标的资产越有可能敲出或敲入障碍值。例如,向上敲出失效看涨期权(UOC)和向下敲出失效看跌期权(DOP)随着波动率值越大,其期权价格越便宜。通过上述算法模拟可以得到欧式看涨期权价格等于向上敲出失效看涨期权和向上敲入生效看涨期权价格之和,也等于向下敲出失效看涨期权和向下敲入生效看涨期权价格之和,同样,欧式看跌期权价格等于向上敲出失效看跌期权和向上敲入生效看跌期权价格之和,也等于向下敲出失效看跌期权和向下敲入生效看跌期权价格之和。由于篇幅有限,这里只列出σ取值不同时,向上敲出敲入看涨看跌障碍期权定价算法结果对比,向下敲出敲入看涨看跌障碍期权定价算法结果对比略,可联系作者获得。 四、結论 随着新冠疫情大流行的结束和经济开始复苏,负油价更多地作为极端事件,已经被量化分析师从估值模型中剔除这些异常值。但是在这个全球化日益发展的时代,宏观环境瞬息万变,另一场油价动荡完全可能再一次冲击金融市场的交易逻辑,使模型的转换和更改变得日益频繁,如何确保转换模型有效且平稳对金融市场至关重要。 本文在负标的资产价格的启发下,研究基于O-U特征的Bachelier模型的期权定价有效性,通过结合蒙特卡洛数值模拟方法拓展其在美式期权和障碍期权上的应用。本文致力于将Bachelier模型期权定价纳入金融衍生品定价中,为期权定价做出指导决策,也为市场投资者调整交易策略和投资组合提供理论指导和审慎风险管理。 参考文献 [1]张婧,王佩WTI负价格形成的深层次原因分析[J]国际石油经济,2020,28(6):58-65 [2]吕行从“负油价”视角透析衍生品价值管理[J]中国能源,2020,42(6):13-16 [3]尚全彪负油价带来的思考[J]中国金融,2020(11):87-88 [4]HOMAYOUN B R,THOMAS P,CHRISTIAN UNegative oil price shocks transmission:The comparative effects of the GFC,shale oil boom,and Covid-19 downturn on French gasoline prices[J]Research in International Business and Finance,2021,58(2):101455 [5]部慧,陆风彬,魏云捷“原油宝”穿仓谁之过?我国商业银行产品创新的教训与反思[J].管理评论,2020,32(9):308-322 [6]CHOI J,KWAK M,TEE C W,et alA black-scholes users guide to the Bachelier Model[J]Journal of Futures Markets,2022,42(5):959-980 [7]BACHELIER LTheorie de la Speculation[J]Annales Scientifiques de l Ecole Normale Superieure,1900(17):21-88 [8]SCHACHERMAYER W,TEICHMANN JHow close are the option pricing formulas of Bachelier and Black-Merton-Scholes?[J]Mathematical Finance,2008,18(1):155-170 [9]JOSHI M S,REBONATO RA displaced-diffusion stochastic volatility LIBOR market model:Motivation,definition and implementation[J]Quantitative Finance,2003,3(6):458-469 [10]BLACK F,SCHOLES MThe pricing of options and corporate liabilities[J]The Journal of Political Economy,1973,81(3):637-654 [11]MERTON R CThe theory of rational option pricing[J]The Bell Journal of Economics and Management Science,1973,4(1):141-183 [12]BROOKS R,BROOKS J AAn option valuation framework based on arithmetic brownian motion:Justification and implementation issues[J]Journal of Financial Research,2017,40(3):401-427 [13]RENDLEMAN R J,BARTTER ATwo-state option pricing[J]The Journal of Finance,1979,34(5):1093-1110 [14]LONGSTAFF F A,SCHWARTZ E SValuing American options by simulation:a simple least-squares approach[J]The Review of Financial Studies,2001,14(1):113-147 [15]OCHOA C MMonte carlo option pricing[J]Lecturas de Economía,2004(61):53-70 Option Pricing of Bachelier Model Based on O-U Characteristics QIAN Weijia1 CHEN Haifeng1 CHEN Angang1 LV Zhaojin1 XI Lei2 (1GuotaiJunan Securities Co,Ltd,Shanghai 200042,China;2College of Management,Anhui Science and Technology University,Chuzhou 233100,China) Abstract:With the emergence of “negative oil prices”,the negative price of underlying assets for options and other derivatives means the failure of the classic Black-Scholes modelThe original Bachelier model is modified in this paper to preserve the feature that the underlying asset price can be negative and make it have the Ornstein-Uhlenbeck stochastic process featureBased on the modified Bachelier model combined with Monte Carlo numerical algorithm to price European option,American option and Barrier option,further expand its application range of option pricingThrough numerical simulation,the modified Bachelier model shows high computational accuracy in option pricingThe option pricing of the Bachelier model based on O-U characteristics can be used as an alternative to the Black-Scholes model and guide the pricing decisions of options and other derivatives Key words:Black-Scholes Model;Bachelier Model;Option Pricing;Barrier Option;Negative Underlying Assets
