同轴送粉激光熔覆粉束质量分布密度模型与实验测量
2023-09-18王军华许俊飞彭建军李东林颉潭成
王军华,许俊飞,路 妍,彭建军,李东林,颉潭成
(1.河南科技大学 a.机电工程学院;b.材料科学与工程学院,河南 洛阳 471023;2.河南省智能制造装备工程技术研究中心,河南 洛阳 471003;3.智能数控装备河南省工程实验室,河南 洛阳 471003)
0 引言
同轴送粉式激光熔覆技术是以高能量密度激光束为移动热源,以金属粉末为成形材料,根据预先规划的扫描路径逐道扫描实现金属零件表面改性,达到强度增加和耐磨性提升的目的[1-3]。粉束内粉末颗粒的空间质量分布密度是决定激光熔覆几何形状尺寸的关键核心问题之一[4]。掌握同轴送粉粉束汇聚特性及空间质量分布是精确控制激光熔覆过程中单道沉积层截面形状尺寸的前提。
国内外科研工作者采用数值模拟仿真、理论模型推导及实验检测等手段,研究送粉喷头结构及尺寸、粉末颗粒形状及大小、载气流量及送粉速率等因素,对粉束运动轨迹、汇聚特性的影响。文献[5]采用欧拉-拉格朗日框架,建立了1个四流道气-粉喷嘴的流体动力学模型来分析送粉过程。结果表明:当内层气体和载气的速度相等时,由于形成了稳定的层状粉末流,粉末流在熔池区域表现出最佳浓度。文献[6]利用点-粒子大涡流模拟和高速成像,研究壁面粗糙度和粉末颗粒大小对从垂直圆形喷嘴发出的粉末流动特性的影响。结果显示:壁面粗糙度增强了粉末颗粒的横向分散性,并消除了颗粒在近壁区域的优先积累,导致了喷嘴内平均颗粒速度的降低和颗粒在喷嘴核心的聚集。文献[7]通过基于高斯光束的射线表示法对粉末流进行建模,并通过高速相机进行实验验证。结果表明:在喷嘴出口位置,由高速摄像机粒子跟踪获得的粉末流的统计数据与该模型相符。文献[8]为阐明粉末颗粒在连续同轴送粉过程中的传输机制,开发了一种试验和匹配方法来量化,用于描述颗粒与喷嘴壁之间非弹性碰撞的恢复系数。研究发现,外层屏蔽气体流对多层射流流场有很大影响,在外层屏蔽气体流为20 L/min时,最有利于粉末聚焦。文献[9]采用雷诺平均Navier-Stokes方程进行数值模拟,在不同实验条件条件下分别进行试验。结果显示:仿真结果与实验结果具有良好一致性,且气体流速、粉末流速和喷嘴结构均对粉末流直径有影响。文献[10]以粉末流的焦距和有效粉斑直径为研究对象,分析了载气、同轴保护气、送粉速率对粉末束流关键特征的影响规律,为粉末流调控提供依据。文献[11]基于气固两相流原理,通过建立三维粉末流输送模型,分析了弹性恢复系数对同轴喷嘴外流粉末场的速度场、浓度场、焦点距离和粉斑尺寸的影响。综上可知,国内外研究人员针对侧向送粉或同轴环形送粉模式,在粉束汇聚特性[12-13]、粉束内粉末颗粒空间质量分布密度[14-16]等方面做了大量研究,取得了一些成果,但研究多采用数值模拟开展,而目前应用广泛的多粉针同轴送粉模式涉及较少。
为了实现四粉针同轴送粉模式下粉束空间质量分布密度的全参数化准确预测,本研究根据送粉喷头结构参数和送粉工艺参数,建立粉末空间质量分布密度全参数化理论计算数学模型,并提出一种简易的粉束内粉末颗粒空间质量分布密度实验检测方法,以验证所建粉束空间质量分布密度理论模型的正确性与有效性。
1 数学模型
四粉针同轴送粉喷嘴结构模型及其粉末流示意图,如图1所示。在粉末输送过程中,粉末颗粒在载
气作用下与送粉管道及粉针内壁反复碰撞,单个粉末颗粒的运动并非沿粉针中心射出,致使整个粉束在出粉口有一定发散,在成形基面上并未汇聚一点而是一个区域。由图1可知:不同粉针喷射粉束在与出粉口垂直距离fb处汇聚为一点,此时,fb为焦距,θ为粉束发散角,α为粉针与成形基面夹角。
1.1 单粉针粉束质量分布密度数学模型
在建立单粉针粉束质量分布密度数学模型前,需作出基本假设[17-18]:若要建立单粉针粉束在空间任意平面内粉末质量分布密度数学计算模型,则应将其在垂直粉管轴线上相应平面内的高斯分布函数进行几何关系转化。空间任意平面内单粉针粉束质量分布密度几何关系转化示意图如图2所示。
通过引入离焦量的影响,以(fb+DL)作为限定目标平面位置变量,表示目标平面至粉针出粉口的垂直距离。单粉针粉束在垂直于粉针中心轴线X0O0Y0平面内服从高斯分布,在该平面内其粉末质量分布密度可表示为:
(1)
其中:r0为X0O0Y0平面内粉束半径,mm,其大小随垂直于粉针中心轴线平面位置的改变而变化。同时,若要根据X0O0Y0平面内粉束质量分布密度,通过理论计算获得X1O1Y1平面内粉束质量分布密度,需对图2中各参数之间的关系进行几何换算,各参数间关系可由公式(2)表示:
r0=r′+Ltanθ;
(2)
(3)
(4)
(5)
其中:r′为单粉针出粉口半径, mm;L为X0O0Y0平面沿粉针中心轴线方向至出粉口距离,mm;fb为粉斑焦距,mm;DL为离焦量,mm;α为单粉针与成形基面夹角,其取值应视具体送粉喷头结构而定,本研究所用送粉喷头α为65°;D为粉针出粉口间距,mm, 本研究所用送粉喷头D为15.6 mm。
针对单粉针喷射粉束,当送粉工艺参数一定时,送粉过程是稳定的,可以认为粉束空间内某点处粉末质量分布密度恒定不变。而该点处粉末质量分布密度函数表达与所考察目标平面有关,有:
f1(x1,y1)Δx1Δy1=f0(x0,y0)Δx0Δy0。
(6)
由公式(4)和公式(6)可知,空间任意平面内某一点P处粉末质量分布密度函数可表示为:

(7)
1.2 四粉针粉束质量分布密度数学模型
四粉针同轴送粉模式粉束在空间任意平面内粉末质量分布密度坐标转换示意图如图3所示。由图3可知,由于四粉针同轴送粉喷嘴空间结构的对称性以及送粉参数一致性,各粉针喷射粉束在目标平面内的形状尺寸完全相同,只是方向和位置存在一定差异。在XOY平面内通过沿坐标原点O旋转,则可以实现彼此完全重叠。通过对4个不同粉针喷射粉束在XOY平面内的粉斑建立如图3所示坐标系,则可通过公式(7)计算不同粉束在各自坐标系内的粉末质量分布密度,然后利用坐标转换公式(8),可将其转化为XOY平面内的粉末质量分布密度函数。

图3 四粉针同轴送粉喷嘴粉束在空间任意平面内粉束坐标转换示意图
坐标系转换关系可以表示为:
(8)
由于公式(1)是经过归一化处理后的粉末质量分布密度模型,由此推导出的公式(7)也是归一化模型。为了实现真实送粉工艺参数条件下,四粉针同轴送粉模式下粉束粉末质量分布密度预测计算,需要引入送粉速率,并将其送粉量均匀分散在四粉针内,同时结合坐标转换公式(8),可将空间任意平面内某一点P处的粉末质量分布密度函数表示为:
(9)
另外,发散角θ可由公式(10)给出[19]:
(10)
其中:ν为载气运动黏度,mm2·s-1;V0为载气流速,mm·s-1,可以表示为:
(11)
其中:Lp为载气流量,L·min-1;rpipe为输粉管内径,mm。
对于具体送粉喷头而言,结构尺寸固定,相应参数均为常数,比如粉针轴线倾角、出粉口半径、粉针出粉口间距等。因此,针对四粉针同轴送粉模式来说,真正影响粉束内粉末颗粒空间质量分布密度的只有送粉速率和离焦量。
1.3 同轴送粉模式粉束质量分布密度Matlab计算
不同离焦量四粉针同轴送粉模式下,粉束在空间任意平面内汇聚情况示意图如图4所示。由图4可知:当目标平面位于焦平面上方时,其离焦量为负值,此时单个粉针喷射粉束未到达焦点位置,各自靠近出粉口位置,各粉束未完全汇聚,激光束辐照O点处粉末质量分布密度较小,当离焦距离较大时,O点处粉末质量分布密度甚至为0;同样,当目标平面位于焦平面下方时,其离焦量为正值,此时单个粉针喷射粉束越过焦点位置,使得各粉束无法完全汇聚,激光束辐照O点处粉末质量分布密度也有所降低,不同的是此时总有粉末颗粒被激光束辐照。

图4 不同离焦量条件下四粉针同轴送粉模式下粉束汇聚情况示意图
为了研究不同离焦量条件下目标平面内粉束质量分布密度特征,利用Matlab软件对公式(9)进行计算,进而定量计算了不同成形基面上粉束质量分布密度函数fp(x,y),计算所用各参数如表1和表2所示。

表1 理论计算所用送粉工艺参数

表2 理论计算所用送粉喷嘴结构参数
不同离焦量条件下,目标平面内粉束质量分布密度理论计算结果如图5所示,XY平面为考察目标平面,该考察目标平面内不同位置处粉末质量分布密度如纵坐标所示。如图5a所示,当考察目标平面在焦平面上方且离焦量较大时,四粉针同轴送粉喷嘴喷射粉束在此平面内并未汇聚,各粉束喷射粉末颗粒在XY平面O点位置(激光束辐照位置)只有极少一部分,致使此处粉束质量分布密度相对较小,相应地在激光熔覆时粉末利用率较低。由图5b可知:当考察目标平面在焦平面附近时,四粉针同轴送粉喷嘴喷射粉束汇聚特性较好,在XY平面O点位置(激光束辐照位置)粉末质量分布密度相对较大,分布特性近似高斯分布特征。尤其是在离焦量为0的焦平面上,粉束汇聚特性最好,粉束质量分布密度呈现高斯分布特征,即在激光辐照位置粉末质量分布密度达到最大值,相应地在激光熔覆过程中粉末利用率也将最大。由图5c和图5d可知:当考察目标平面在焦平面下方且离焦量较大时,在XY平面O点位置(激光束辐照位置)粉末质量分布密度显著下降,同时粉束汇聚特性变差,粉斑尺寸明显增大。由此可知,当考察目标平面偏离焦平面时,无论离焦量为正还是负,随着离焦量绝对值的增大,考察目标平面上粉斑尺寸逐渐增大,激光束辐照位置处粉末质量分布密度逐渐减小[124]。

(a) DL=-3.5 mm
由于四粉针同轴送粉喷嘴结构的对称性,粉束质量分布密度曲线在X轴和Y轴线完全相同。不同离焦量条件下X轴线截面内粉末质量分布密度如图6所示。从图6中明显看出:当离焦量不同时,X轴线截面内粉末质量分布密度差异显著。当离焦量为0 mm时,粉末质量分布密度曲线呈现高斯分布特征,激光辐照区域内粉末质量分布密度最大;当离焦量在±1.5 mm范围内时,X轴线截面内粉末质量分布密度基本服从高斯分布,粉束汇聚特性相对较好。随着离焦量的增大,无论是正离焦还是负离焦,粉束汇聚特性显著变差,激光辐照区域内粉末质量分布密度显著降低。

图6 不同离焦量条件下X轴截面内粉末质量分布密度对比
2 实验研究
2.1 粉束质量分布密度测量方法
粉束内粉末质量分布密度的准确测量十分困难,原因就在于送粉过程为动态过程,且不同水平面内粉束形状及质量分布密度均存在差异[20]。若要实现空间任意平面内任一位置处粉末质量分布密度的准确测量,核心问题则是目标平面内待考察位置处粉末颗粒的高精度收集与测量。为了解决这一问题,提出利用内径为0.5 mm的铜管作为集粉管,在单位时间内较为精确地收集粉束内待考察位置粉末颗粒并称质量,然后计算出该位置的粉末质量分布密度。如果单位时间内,运动到粉束内某位置处(单位面积)的粉末颗粒质量已知,此时粉末颗粒质量则为该位置处的粉末质量分布密度,由此则有:
(12)
其中:fc(x,y)为目标平面待考察位置处粉末质量分布密度,g·mm-2·min-1;mc为集粉器内粉末颗粒质量,g;rc为测量铜管内径,mm;tc为测量用时,min。
粉末质量分布密度实验测量方法示意图如图7所示。由图7可知:将内径为0.5 mm的铜管放置于粉束区域目标平面待考察位置处,确保集粉铜管顶部端面与目标平面重合。在预设送粉参数条件下打开送粉装置,粉束内待考察位置处粉末颗粒将射入集粉铜管管口区域内,并沿集粉铜管内壁自由下落进入集粉器,以2 min为计时单位,利用电子天平称量集粉器内收集的粉末质量,然后利用公式(12)计算出粉末质量分布密度。通过不断变换目标平面待考察点的位置,重复上述操作,则可实现目标平面不同位置处粉末质量分布密度测量。

图7 粉束质量分布密度实验测量方法示意图
2.2 粉束质量分布密度测量装置及参数选择
实验所用粉材为17-4PH,粉末形貌及粒度分布分别如图8和图9所示,粉末密度为7.9 g·cm-3。实验参数如表3所示。实验所用粉材为马氏体沉淀硬化不锈钢(17-4PH)粉,粉末颗粒呈圆球形,粒度为50~110 μm。由图8和图9可知:实验所用马氏体沉淀硬化不锈钢(17-4PH)粉材粒度均匀,粒度主要为80~90 μm。
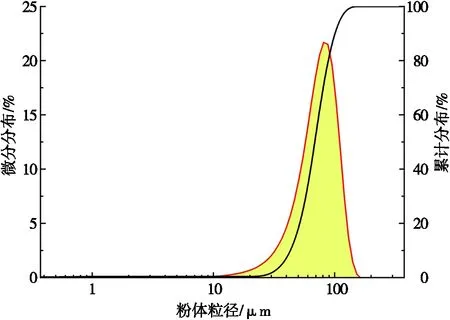
图9 马氏体沉淀硬化不锈钢(17-4PH)粉末颗粒粒度分布 (120倍)

表3 实验所用参数
实验检测过程是将内径为0.5 mm的集粉铜管连同集粉器一起固定在机床工作台上,通过调整数控机床工作台,确保集粉铜管顶部端面与目标平面重合,并放于粉束区域目标平面待考察位置处。然后,在预设送粉参数条件下打开送粉装置,以2 min为计时单位,计时结束后利用电子天平称量集粉器内收集的粉末质量。此后,通过控制数控机床工作台将集粉管移动至下一测量点,重复上述操作。在每个目标平面内,测量点如图10所示,分别沿如图10所示XY轴每隔1 mm测量1个位置点,每个目标平面内共测17个位置点。
为了考察不同离焦量条件下粉末质量分布密度变化情况,通过三轴联动数控装置控制激光喷头沿Z轴移动,调整其与集粉铜管顶部端面间的距离,实现离焦量的调整。本实验研究共检测3个目标平面,其离焦量分别为 -3.5 mm、-1.5 mm、0 mm、5.5 mm,每个目标平面内共检测17个考察位置点,每个位置点重复测量3次求取平均值,然后分别代入公式(12),计算相应考察位置处粉末质量分布密度。
3 分析讨论
不同目标平面内X轴不同位置处粉末质量分布密度实验测量结果如图11所示。由图11可知:不同目标平面内,粉束内粉末质量分布密度差异显著。不同目标平面以及同一目标平面的不同位置处,粉末颗粒质量分布密度存在显著差异。如图11c所示,当目标平面离焦量为 0 mm时,粉束内在X轴截面内粉末质量分布密度呈现近似高斯分布特征,相比其他目标平面而言,此时在激光辐照O点位置粉末质量分布密度最大,而且粉束尺寸最小,汇聚特性最好。当目标平面离开焦平面,即有一定离焦量时,无论离焦量为正还是为负,激光辐照位置(X轴原点O)粉末质量分布密度均出现不同程度下降,且偏离焦平面距离越远,粉末质量分布密度下降越显著。与正离焦不同的是,当目标平面离焦量为-3.5 mm时,粉束内在X轴截面内粉末质量分布密度不再服从高斯分布,而是呈现双驼峰分布特征,如图11a所示,这说明此目标平面内多粉口喷射出粉末流并未汇聚一处。

(a) DL=-3.5 mm
结合不同目标平面内X轴不同位置处粉末质量分布密度实验测量结果,将其与理论计算结果进行对比分析,进一步验证前文所建立的粉末质量分布密度理论计算模型的正确性。不同目标平面内X轴不同位置处粉末质量分布密度理论计算与实验检测结果对比如图12所示。由图12可知:不同目标平面内X轴不同位置处粉末质量分布密度理论计算与实验检测结果吻合较好,不同目标平面内粉末质量分布密度理论计算结果和实验检测结果变化趋势完全相同,尤其是目标平面接近焦平面时(离焦量较小情况),在激光辐照位置处二者高度吻合,接近100%(如图12b和图12c所示),说明前文所建立理论计算模型可以用于四粉针同轴送粉模式下粉束内粉末质量分布密度的准确计算。
然而,理论计算与实验检测结果之间也存在一定偏差,如图12d所示O点附近和图12b~图12cO点两侧2~4 mm处,偏差相对较大。分析认为,造成理论计算和实验检测结果出现误差的原因可能是实际送粉过程中单粉针喷射粉束发散角大于理论计算值(如图13所示),由于建立粉束质量分布密度理论模型时假定单粉束粉末颗粒运动至发散角以外的可能性为0,而实际送粉时极有可能出现部分粉末颗粒射出理论发散角以外,即实际发散角大于理论发散角,此时运动至A区域粉末颗粒增多,导致图12a中激光辐照区域粉末颗粒增大,相应粉末质量分布密度大于理论计算值。同理,由于实际发散角偏大,运动至B区域内的粉末颗粒也增多,导致实验检测时图12b~图12c中激光辐照区域两侧2~4 mm处粉末质量分布密度大于理论计算值。而在如图13所示C区域内,粉末质量分布密度增大的原因可能是不同粉针喷射出粉束在聚焦点处汇聚,粉末颗粒相互之间的碰撞或者在其他粉束载气作用下,粉末颗粒水平运动速度降低,致使粉束内多数粉末颗粒下落在C区域,导致此处实验测量数值高于理论计算数值,这或许就是图12d所示粉末颗粒质量分布密度实际测量值大于理论计算值的原因所在。

(a) DL=-3.5 mm

(b) DL=0 mm

(c) DL=3.5 mm

(d) DL=5.5 mm
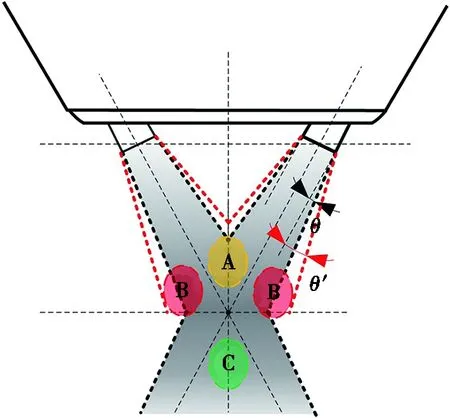
图13 粉束发散角对粉末质量分布密度影响分析示意图
4 结论
(1)空间任意平面内粉束质量分布密度主要取决于送粉速率、离焦量和送粉喷头结构尺寸等参数;对具体送粉喷头而言,结构尺寸固定,而真正影响粉末质量分布密度的因素,则是送粉速率和离焦量;
(2)不同目标平面内,粉束内粉末质量分布密度差异显著。当目标平面有一定离焦量时,无论正离焦量还是负离焦,光斑处粉末质量分布密度均下降,且离焦量越大下降越显著。
