偏微分方程建模的多智能体系统的一致性

栗素娟, 许珂欣, 孙祥亮, 宋 帅

(1．河南科技大学 信息工程学院, 河南 洛阳 471023; 2．平顶山技师学院 基础部, 河南 平顶山 467000)

0 引言

近年来,多智能体系统在理论研究和工程应用方面都取得了快速发展,如飞行器的协同控制、机器人系统的编队控制和电力系统等[1-3]。一致性问题作为多智能体系统中的热门话题有着丰硕的成果。例如,文献[4]研究了基于采样数据的一致性控制;文献[5]考虑了非线性多智能体系统在事件触发下的一致性;文献[6]研究了切换拓扑下多智能体系统的一致性。需要注意的是,以上的结果都集中在常微分方程描述的质量一致性上。这意味着系统只能获得单个智能体的一维状态信息,如速度和加速度等。然而,许多系统的动力学不仅依赖于时间,而且依赖于空间,这意味着使用偏微分方程(partial differential equation, PDE)为单个智能体建模是有意义的[7-9]。与基于常微分方程的多智能体系统控制相比,分布参数多智能体系统的控制由于其无限维特性而更加难以分析。如何获取基于PDE的多智能体系统的一致性成为一个具有挑战性的问题。文献[10]研究了时空系统的同步和稳定性分析,为本文的研究提供了一种有效的方法。到目前为止,基于PDE的多智能体系统的一致性还没有得到充分的研究。这激发了本文研究构建基于PDE的多智能体系统模型,并研究其动态性能。

多智能体系统根据是否有领导者的加入可以分成两类,在带有领导者的多智能体系统中,跟随者需要和领导者的状态保持一致从而实现总体的一致性[11],而在无领导者的系统中,智能体通过邻居间的信息交流实现控制目标[12],二者在控制协议上有所不同。前者的优点在于只要人为操控领导者,就能实现整体的控制,而缺点也是很明显的,如果领导者遭到破坏,整个系统容易崩溃;无领导者的系统则避免了这一问题,但缺点在于控制协议复杂,需要使用更多的资源[13]。

为了使多智能体系统能够获得更全面的信息,本文将空间变量引入单个智能体,构建了基于PDE的多智能体系统[14-17]。为了实现系统的一致性分析,将PDE系统中常用的计算方法引入多智能体系统,并针对系统有无领导者的两种情况分别进行了一致性分析,并给出了相应的充分条件,结果用线性矩阵不等式展现。最后,两个数值例子被给出,用来验证本文所提的理论。

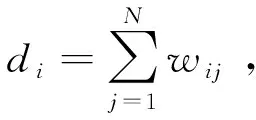
1 领导者-跟随者多智能体系统的一致性

本文考虑的非线性领导者-跟随者多智能体系统采用抛物型偏微分方程为基础,其中,领导者有如下形式:

yt(x,t)=yxx(x,t)+f(y(x,t))。

(1)

系统的边界条件和初始条件为:

yx(x,t)|x=l1=yx(x,t)|x=l2=0,y(x,0)=φ(x),

(2)

其中:y(x,t)∈L2([l1,l2];Rn)是系统状态;f(·)是光滑的非线性函数。

此外,考虑N个跟随者的模型为:

si,t(x,t)=si,xx(x,t)+f(si(x,t))+ui(x,t),

(3)

同时,满足以下条件

si,x(x,t)|x=l1=si,x(x,t)|x=l2=0,si(x,0)=φi(x)。

(4)

假设1对于所有x1≠x2,x1,x2∈R,存在1个正标量,使得|f(x1)-f(x2)|≤|x1-x2|成立。

假设2跟随者(3)和领导者(1)的通信拓扑包含以领导者为根的有向生成树。

定义误差为ei(x,t)=si(x,t)-y(x,t),根据式(1)和式(3)可以得到误差系统为:

(5)

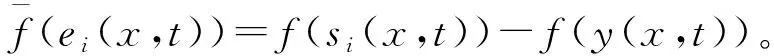
(6)

定理1基于PDE的有领导者的多智能体系统(1)～(4)可以实现一致性控制,如果存在正常数c和正定矩阵Ξ使得下式成立:

(7)

证明选择如下李雅普诺夫函数:

(8)

对V(t)沿着式(6)进行求导,可得:

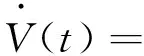
(9)

根据分部积分法和文献[18]中的引理1,可得:

(10)

此外,利用一些基本不等式,可知下式成立:

(11)

结合假设1和式(11)可以计算出:

(12)

通过分析式(9)～式(12)可以得出:

(13)

根据定理1和李雅普诺夫稳定性分析,可以推断出基于PDE的具有领导者的多智能体系统(1)～(4)可以实现一致性。定理1证毕。

2 无领导者多智能体系统的一致性

本节研究的基于PDE的无领导者多智能体系统有如式(3)的形式,且非线性函数同样满足假设1。同上节相似,需要对无领导者系统的拓扑结构做出假设:

假设3N个无领导者的拓扑结构是强连通的。

(14)

定理2基于PDE的无领导者多智能体系统(3)可以实现一致性控制,如果存在正常数c和正定矩阵Λ使得下式成立:

(15)

证明选择如下李雅普诺夫函数:

(16)

通过与定理1相似的证明,可得:

(17)

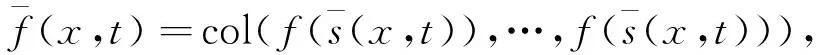
(18)

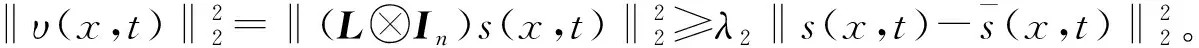
(19)

结合定理2可以说明基于PDE的无领导者多智能体系统(3)可以实现一致性。定理2证毕。

3 仿真实验

3.1 具有领导者的多智能体系统

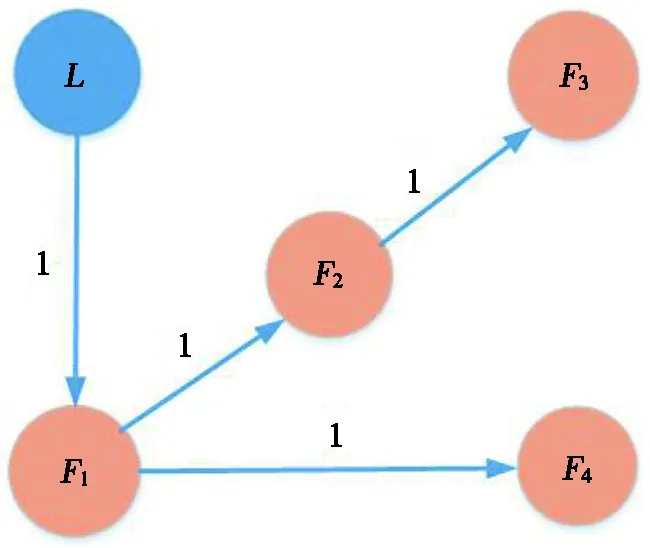
图1 具有领导者的多智能体系统的拓扑结构图

为了验证定理1的有效性,本例考虑具有1个领导者和4个跟随者的基于PDE的多智能体系统,其拓扑结构如图1所示。相关参数为f(x)=arctan (x),c=5.73,l1=0,l2=1。

系统初始条件为:

误差系统(5)的开环轨迹和闭环轨迹分别如图2和图3所示。图2和图3中,eij表示第i组数据中第j个智能体与领导者的误差。从图2和图3中可以看出,系统在没有控制作用的情况下是无法实现状态一致的,当施加控制作用后,误差系统较快地趋近于0,表示一致性的目的达到。

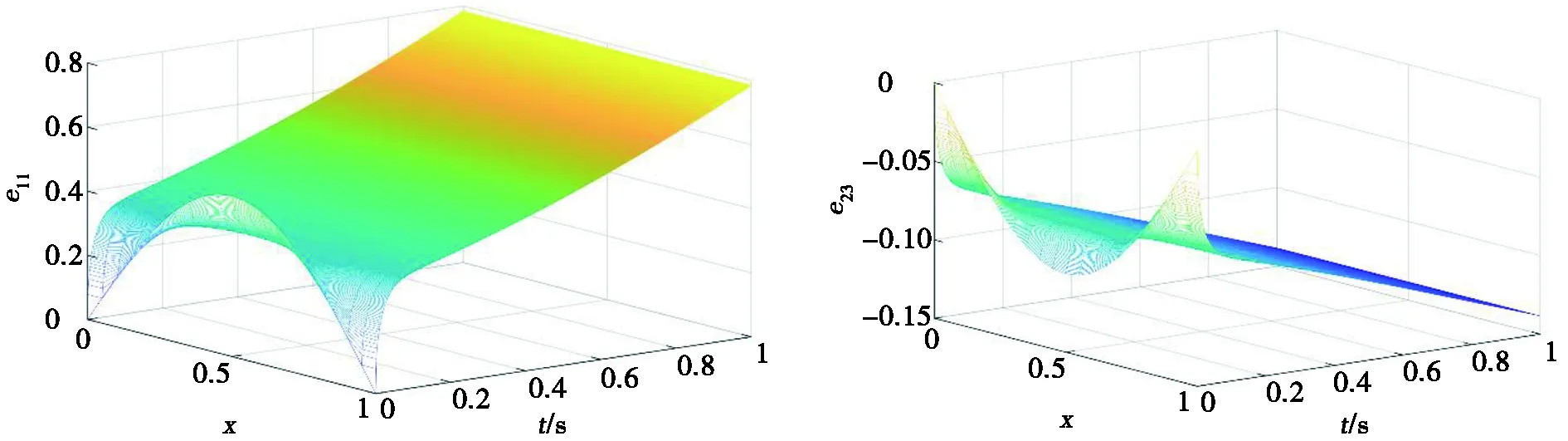
(a) e11开环轨迹 (b) e23开环轨迹

(a) e34闭环轨迹 (b) e31闭轨迹

3.2 无领导者的多智能体系统

考虑1个由5个智能体组成的无领导者的基于PDE的多智能体系统,其拓扑结构如图4所示。同时,选择非线性函数为f(x)=0.65arctan (x),c=1.32。系统初始条件为φi(x)=isin (πx),i=1,2,…,5。图5和图6分别展示了误差系统(14)的开环和闭环轨迹。图5和图6中,υij表示智能体i和智能体j的误差。从图5和图6中可以看出,基于PDE的无领导者多智能体系统也可以实现一致性控制。本文所得结果在有领导者和无领导者两种情况下均适用,表示所得结果的一般性。

(a) V14开环轨迹 (b) V25开环轨迹

(a) V14闭环轨迹 (b) V25闭环轨迹

4 结束语

本文考虑了单个智能体的空间属性,构建了基于PDE的多智能体系统,并研究了系统在具有领导者和无领导者两种情况下的一致性问题,控制增益的求取以线性矩阵不等式的形式呈现,仿真结果验证了所提方法的有效性。本文所得结果是基于连续控制的方法,此类方法的缺陷是数据量较大,因此,在本研究成果的基础上,基于采样数据的一致性[19]、钉扎同步[20]和脉冲同步[21]等节能同步方法也值得从反应扩散神经网络同步推广到基于PDE的多智能体系统中,这将是作者未来的工作重点。