隐性扰动下智能车间资源重调度决策方法研究＊

2023-09-18苑明海黄涵钰蔡仙仙李子晨裴凤雀

制造技术与机床 2023年9期

苑明海黄涵钰蔡仙仙李子晨裴凤雀

（①河海大学机电工程学院，江苏常州 213022；②常州市智能制造技术与装备重点实验室，江苏常州 213022）

智能制造车间[1]包含各类资源，其可靠性和抗干扰性难以完全保证，造成了车间内无法避免的各式扰动。其中，隐性扰动或累计扰动是一类不可见却又影响着产品制造过程的平稳可靠性的扰动，其往往隐于普通加工过程，难以测量捕捉，并有赖于偏差的累积（如算法寻优导致的单一设备负荷过高、加工精度偏差累计、工件搬运不畅导致的开始加工时间偏差累计等），待隐性扰动累计到一定程度需要进行重调度[2]。

在智能制造现行模式下，利用车间资源实时产生的任务执行数据监测车间内扰动[3]，快速高效的重调度机制为车间资源调度优化提供了基础性的保障[4-7]。目前对隐性扰动下的车间重调度方法研究相对较少[8]，Akkan C[9]采用被动触发式重调度规则对隐性扰动重调度方法进行了研究。唐秋华等[4]利用累积误差时间来量化隐性扰动，提出了一种基于机器学习的重调度方法。刘壮等[10]提出了基于改进逼近理想解排序的车间重调度决策方法。Tian S L 等[11]提出了基于培养网与蚁群优化算法，引入门槛值触发的机制，实现车间自适应重调度。Kumar N 等[12]提出了一种基于布朗运动加权的小群算法，建立了扰动分析和重调度的有效方法。李聪波等[13]提出了一种改进的引力搜索算法，以节能优化为目标进行紧急插单类动态扰动的车间重调度方案求解。Moser M 等[14]运用元启发方法解决不相关并行机器调度问题。

由于隐性扰动影响生产过程周期长，且难以监测，现有的重调度研究集中于显性扰动情况下的重调度方法，普通重调度策略难以适用。因此本文着眼于隐性扰动下车间资源重调度方法，研究隐性扰动造成的资源状态异常检测方法，并利用数据替代手段研究智能制造车间调度切换过程中的短暂容错机制，量化隐性扰动后快速确立重调度时刻点，分类并抉择重调度方式以指导智能车间在隐性扰动情况下的高效生产。实现制造系统监测到隐性扰动之后、生产进程宕机之前选择正确的重调度策略，降低最大完工时间和交付延时均值，并降低加工成本的目标。智能制造车间隐性扰动应对流程如图1 所示。

图1 智能制造车间隐性扰动应对流程

1 隐性扰动下车间资源多目标重调度问题

1.1 问题描述

智能制造车间的典型特征是离散化柔性化，现将智能制造车间多品类产品柔性调度问题描述为：制造准备阶段，一个典型智能制造车间有m台可用于制造多种品类产品的加工中心，n个未加工且工艺不同的工件，每个工件拥有符合工艺路线的工序数目，且加工次序必须合乎工艺路线的规定。每道工序都拥有各自的加工中心集，且只能选取其中一台加工中心进行产品制造，不同加工中心完成各工序的时间各不相同。

在建立具体的数学模型之前，依据智能车间实际生产情况抽象出如下共性的约束规则：

（1）制造任务开始前，各加工中心均处于不工作状态。

（2）一个工件的一道工序仅可由一台加工中心完成。

（3）一台加工中心只有完成上一工序的加工后方可开始下一任务。

（4）所有工件在每台加工中心上的优先级相同。

（5）各工序的加工过程除意外不会无故中断。

（6）工件的安装卸载搬运操作均计入该道工序的完成时间内。

本文中出现的符号定义见表1。

表1 符号定义表

1.2 模型建立

车间调度的含义是综合利用车间制造资源，合理分配给每个工序相应的资源，以此达到既定目标函数的最大值或最小值而智能制造车间调度则是将多目标综合优化刻入到每一个智能制造环节。因此本文选取如下对车间实际生产影响较大的参数，建立相应的目标函数，以此达到按期完成生产任务、合理配置车间设备资源、缩短客户等待时间和降低生产成本的目的，实际性地解决智能制造车间多品类产品柔性调度问题，数学模型如下：

（1）最大完工时间为

（2）交付延时均值=各工件的交付延时总和/工件总数目。

（3）加工中心负载率=所有加工中心的总负载时间/所有加工中心的总开机时间。

（4）总加工成本=所有加工中心的总空载费用+所有加工中心的总工作费用+总延时费用+车间固定成本+车间内总搬运成本。

（5）最优解集，上述4 个指标的值最小为目标最优。

调度过程与实际车间生产的相符程度需要依靠一系列规则的约束，相应的约束规则表示为

（1）一个工件的一道工序仅可由一台加工中心完成。

（2）每个工件的加工次序必须合乎工艺路线的规定。

（3）一台加工中心只有完成上一工序的加工后方可开始下一任务。

（4）各工序的加工过程除意外不会无故中断，工件的安装卸载操作均计入该道工序的完成时间。

（5）制造任务开始前，各加工中心均处于不工作状态。

（6）每道工序拥有各自的加工中心集，且只能选取其中一台加工中心进行制造。

2 隐性扰动下资源异常状态监测及容错机制

隐性扰动发生时车间需要快速高效重排，以节省中断成本，降低交付延时。虽然现行的技术获取任务执行数据较为容易，但隐性扰动反映在单个数据层面的差异过小使得容易被终端数据监控系统所忽略。因此本文设计了基于软测量模型的任务执行异常数据监测模型和使用数据替代方法的短暂容错机制，将软测量模型计算出的预测值替换掉异常的任务执行数据，使得生产过程短暂正常运行。

2.1 资源异常状态监测模型

软测量技术[15]对任务执行数据的连续监测效能高，对资源异常状态敏感，对重调度触发时刻的确定具有很大的帮助。而支持向量机技术（supportvector-mnachine，SVM）[16]是软测量模型的常用构建手段，其适应性强，样本规模依赖程度低。

为了确定重调度触发时刻，即资源异常状态时刻，将软测量模型获取资源状态数据的预测值与实时采集的任务执行数据进行比对。并引入影响程度INF代之，如式（13）所示。隐性扰动发生起初的影响程度是 0 ≤INF≤d，其中，d为影响程度INF的阈值，将任务执行案例数据经预处理后通过数据挖掘即可得出该值。当INF＞d时，隐性扰动已经累积到可以使原调度方案失效的地步，因此确立此刻为重调度触发时刻，且运行短暂容错机制及生成重调度方案同步开始。

2.2 资源异常状态短暂容错机制

隐性扰动的累积势必会造成智能制造车间资源异常数据的产生，车间资源的任何一个异常数据都可能会导致整体原始调度方案的瘫痪，因此必须探索出合理高效的数据替代手段，在检测出异常数据到切换重调度方案的短时间内进行数据替换，确保重调度时刻非故障资源的继续运行，并称此为短暂容错机制。SVM 模型给出的预测数据常用于替换隐性扰动下监测出的异常值 (xi,yi)，但预测数据的精确性往往达不到保障系统短暂平稳运行的要求，故本节设计了通过结合K邻近值分类算法[17]和lasso回归算法[18-19]提高预测值的精度。

根据案例库中的任务执行数据，以k个与异常值最相邻的案例数据作为邻近值数据集：[(xi1,yi1),(xi2,yi2),···,(xik,yik)]。这k个数据的任务执行情况与异常更正后的资源状态是最相似的，将这些值综合替代预测值，可以提高替代数据的精确性。将这k个案例数据与异常值的距离D作为权重的关键指标，以加权平均方案把各案例数据的输出值乘以对应权重，其总和即是替代数据的目标值。

本文采用的lasso 回归算法其代价函数中包含有L1范数的惩罚项，以确定权重向量 α可以被求解，代价函数具体如下：

其中：yil为实时采集到的任务执行数据，λ‖α‖1为L1范数的惩罚项。考虑到 λ‖α‖1的特殊性，利用坐标下降法求解最佳权重。

在惩罚项中引入次梯度，解决 λ‖α‖1不可求偏导的问题。

此时将寻找最优权重转换为求解最小代价函数，即两个偏导数的和等于0。

以lasso 回归算法改进K邻近值分类得出的预测值，有效保证在任务执行数据样本数量过低情况下依旧能得出准确性较高的预测值，来保障车间调度方案的平稳切换。

3 隐性扰动下车间资源重调度方式选择

3.1 资源重调度方式

现阶段车间资源重调度的方式主要包含有右移与常规处理[20]。因隐性扰动的累积性与非突发性，常见于车间内单个资源上，甚少在多个车间资源上同时发生，故重调度不必对车间宕机右移，因此右移重调度机制不予讨论，仅沿用常规重调度方式。重调度触发时刻，车间内所有工件将分为三大类：待加工、已完工和部分完工。加工中心亦可分为三类：负载、空载和调整中。加工中心的调整时长可通过对案例库历史数据进行数据挖掘来预估。

现阶段研究多将扰动发生时刻指定为受扰动影响的工序的完工时刻，但在车间实际加工过程中，隐性扰动的资源状态异常时刻往往发生于某一加工中心加工某一工序的进程中。因此本文将隐性扰动下的重调度方式分为两类展开讨论。

常规重调度方式即在重调度触发时刻，快速确立工件的释放时刻与加工中心的可用时刻，然后以目标函数最优为导向调用智能优化算法，快速重排剩余工序生成重调度方案。关键工序等比例重调度区别于常规重调度，认定在重调度触发时刻前隐性扰动对工件加工的影响可以被接受，加之短暂容错机制的存在，该道工序的已加工进度被系统认可，当挪换到另一加工中心进行加工时，剩余加工时长依据剩余进度进行等比例换算。T0为重调度触发时刻，此时在隐性扰动影响下的加工中心Mk正在加工工序Oij，其剩余进度为rate=(ETijk-T0)/tijk。挪换到Oij的可选加工中心的任一台加工中心Mi，其相应的加工时长变为=tijk×rate。

3.2 Sigmoid 分类选择

上述两种重调度方式对应着不同的隐性扰动场景，仅通过简单的优化算法分别寻优对比并不可靠，需要通过历史案例数据来训练系统的重调度方式选择能力，以达到系统对隐性扰动的监测、容错、快速抉择、调用算法生成方案、执行重调度的一套快速应对机制。这里定义重调度方式选择变量Y，Y=1代表选择关键工序等比例重调度，Y=0则选择常规重调度。

由于重调度方式选择是一个二元分类问题，本节引入Sigmoid 分类器[17]进行该问题的求解，Sigmoid函数实现了输入值在 [0,1]之间的投影。我们希望分类器的结果=f(x;w;b)拥有这样的特质：若x为实施关键工序等比例重调度来应对隐性扰动所对应的车间资源状态数据，例如该车间资源发生与时间偏差及与设备资源关联的隐性扰动，那么更接近于1；若x为实施常规重调度来应对隐性扰动所对应的车间资源状态数据，例如该车间资源发生与产品质量关联的隐性扰动，那么更接近于0。

重调度方案决策算法的具体流程如下：

Step1：构建训练数据集。系统调用采集得到的隐性扰动发生时任务执行的历史案例数据构成训练数据集：(x1,Y1),(x2,Y2),···,(xn,Yn)。xi∈Rd代表第i个历史案例任务执行方案中的所有属性指标；Yi为第i个案例的重调度方式选择变量，若Yi=1则代表该案例选用关键工序等比例重调度方式，若Yi=0则代表该案例选用常规重调度方式。

Step2：问题转化。Sigmoid 分类器对第i个案例做出的预测是f(xi;w;b)，而实际重调度方式选择情况是Yi，将两者表示为0～1 分布的向量，而后将平均交叉熵确立为损失函数。

此时问题即转换为使得此平均交叉熵与正则项的和最小。

Step3：寻优求解。在建立优化模型之后，需要寻找最优解。通常随机初始化变量，然后用L-BFGS优化算法迭代更新变量。

4 实例验证

本文采用Matlab R2020a 编写上述算法并求解，硬件平台为AMD Ryzen 5 2 600 CPU @3.40GHz，RAM 16 GB。选用某企业智能制造10×10 规模的车间实例数据进行验证，即10 个加工中心加工10 个工件的车间调度问题，并以遗传算法（genetic-algorithm，GA）对该问题求解得到初始车间调度甘特图，具体调度方案如图2 所示，此调度方案中最大完工时间为70 min，交付延时均值为0 min，加工中心负载率59.43%，总加工成本814.04 元。

图2 实例车间调度甘特图

本文依托于某企业智能制造车间的数据采集及预处理方法，连续采集该车间1 个月内的工序实际加工时长数据。表2 给出了重调度发生时刻剩余工序实例数据，依据等比例重调度原则，工序O82在各加工中心上的加工时间也依据比例进行相应的更改。表1 中数据代表各个工件各道工序用不同加工中心加工的时间数值，还给出来了各个工件的交付期。其中“/”表示该加工中心不在该道工序的可选加工中心集中，因此给不出具体数值。其中“N/A”意味着该工件没有明确的交付期，越快越好。表3 为车间内各加工中心的各项成本。

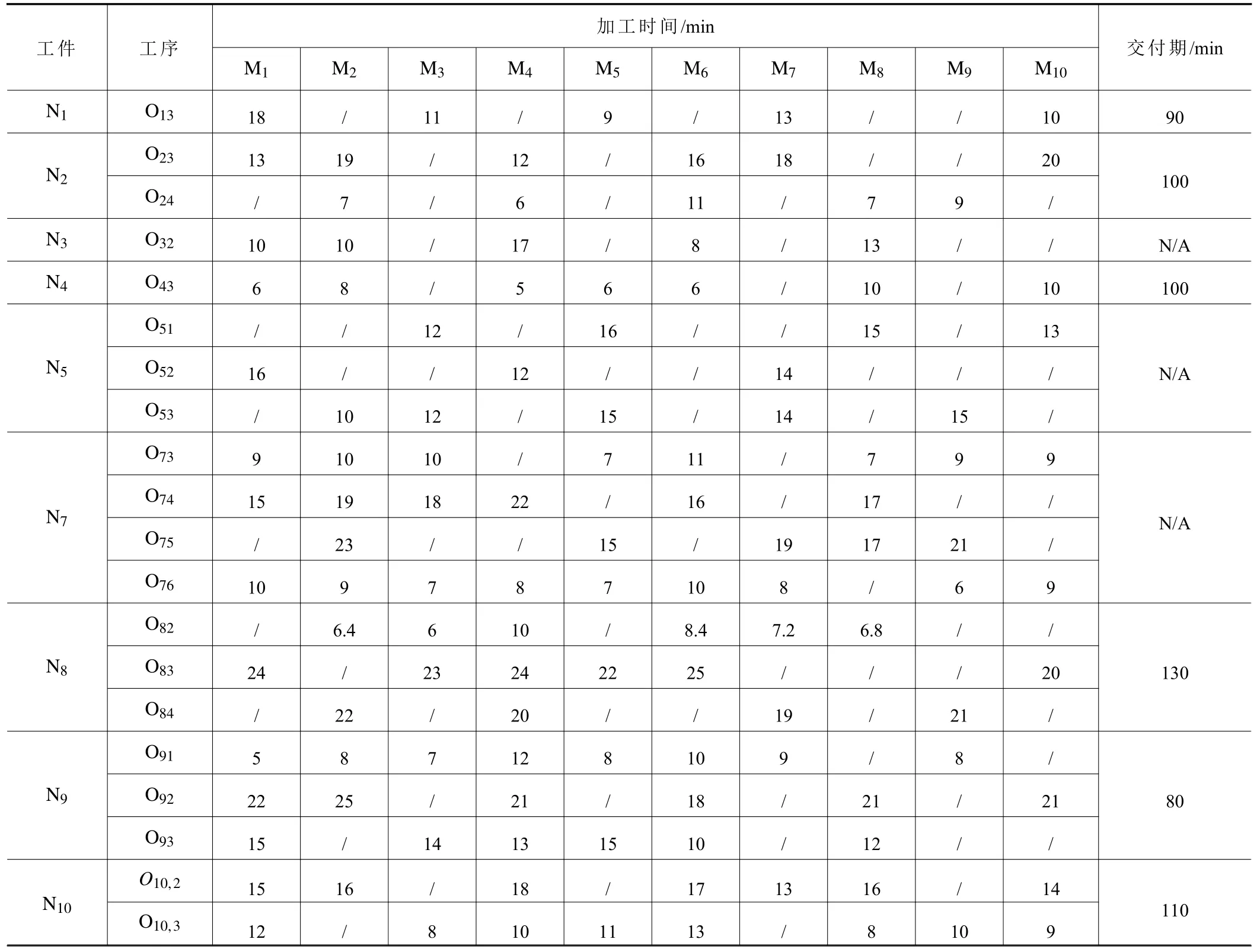
表2 重调度发生时刻剩余工序实例数据

表3 加工中心的各项成本

该智能车间在执行初始调度方案时，资源异常状态监测模型感知到加工中心M8产生隐性扰动，由SVM 模型确定重调度触发时刻为25 min。从历史案例中各加工中心的数据预估出M3的调整时间为25 min，意味着25～50 min 这个时间段内M3不能用于加工。系统调用任务执行数据，通过Sigmoid分类器得出重调度方式选择变量1，由于短暂容错机制的存在，隐性扰动达到影响车间资源正常执行生产任务的阈值前的短暂时刻内，初始调度方案的执行成果是可被接受的。因此判定选用关键工序等比例重调度方案，将当前工序加工结束，以达到最大化减小扰动影响、节省成本并按期交付的目的。而我们回溯任务执行数据发现此刻M3上发生与时间偏差关联的隐性扰动，故系统决策结果正确。具体重调度方案如图3 所示：最大完工时间为73 min，交付延时均值为0 min，加工中心负载率为57.45%，总加工成本为948.17 元。

图3 关键工序等比例重调度甘特图

为了对比关键工序等比例重调度的合理性及有效性，我们假设系统判定此隐性扰动的应对方式为常规重调度，即变量Y=0，则代表着在重调度触发时刻，加工中心上所加工的关键工序O82因隐性扰动的影响无法被系统认可。例如与加工质量关联的隐性扰动，因加工中心M3技术精度误差累积导致工件N8当前的工序延时严重。然后选择重调度方法为常规重调度，将N8的4 道工序重排得具体调度方案如图4 所示。最大完工时间97 min，交付延时均值0 min，加工中心负载率45.36%，总加工成本1 081.00 元。