一种IMNGO-VMD 小样本数据下的轴承故障识别方法

林 伟 曹登学 顾 雨

（上海应用技术大学电气与电子工程学院，上海 201418）

机械轴承[1]是大部分智能化设备必不可少的零件之一，直接影响着设备的稳定和运行安全。越来越多的研究者开始着力于研究轴承的故障识别。想要知道轴承的健康状态，必须处理轴承的振动信号[2]。其中，信号处理[3]是必不可少的过程。信号处理的好坏决定着故障能否被及时发现并排查，但是信号中可能掺杂着各种复杂的特征信号，所以处理起来尤为困难[4]。

徐旺等[5]提出利用改进的虎狼算法优化VMD进行轴承早期故障诊断，张杰等[6]将蝙蝠算法融入到VMD 中在滚动轴承进行故障诊断，朱兴统等[7]利用人工蜂群算法优化VMD 然后进行旋转机械故障诊断，郑义等[8]为了提取滚动轴承故障特征提出基于参数优化的变分模态分解。上述方法都取得了相对理想的实验效果，但都是在大量的实验数据下进行的，在小样本数据下并未取得优异的实验效果，并且存在一定的局部最优现象和缓慢的收敛速度。仇芝等[9]提出CNN-DLSTM 方法结合迁移学习进行小样本的轴承故障诊断，汪祖明等[10]在小样本轴承数据下利用胶囊网络进行轴承的故障识别。上述基于小样本数据下提出的方法都是利用神经网络进行的故障识别，虽然都达到了理想的识别效果，但是都存在故障提取不充分等问题。

因此，为了解决小样本数据下信号提取不充分和识别准确率低等问题，本文在北方苍鹰优化算法的基础上提出一种改进的北方苍鹰优化算法（IMNGO），利用改进的算法联合VMD 进行轴承故障信号的特征提取。该算法用来提高优化VMD 参数过程中的收敛速度，解决局部最优问题。同时该算法通过寻优找到最佳分解层数k，充分提取信号中包含的特征信息。本文最后也将支持向量机（SVM）[11]用IMNGO 算法优化提高识别的准确率。

1 IMNGO 优化算法

1.1 北方苍鹰基础原理介绍

2022 年Dehghani M[12]提出了北方苍鹰优化算法（northern goshawk optimization，NGO）。北方苍鹰的算法过程中主要包含猎物识别和猎物追逐两个阶段。苍鹰的种群用矩阵表示为

式中：X为北方苍鹰的种群矩阵；N为北方苍鹰的种群数量；m为求解问题的维度。

第一阶段：猎物识别（全局搜索）。

式中：FUi位于第i个位置北方苍鹰的目标函数值；表示第i个北方苍鹰在j维度的位置更新；r为[0,1]范围的随机数；I为1 或2 的不确定整数。

第二阶段：猎物追逐（局部搜索）。

假设北方苍鹰的攻击范围半径为R。

式中：t表示当前迭代次数；T表示最大的迭代次数。

1.2 IMNGO 优化算法

1.2.1 混沌映射

在北方苍鹰算法初始化鹰群的过程中，算法随机分布的特性会造成初始种群中鹰群个体分布不均匀的现象[13]。为了解决此类问题，本文引入混沌映射来初始化鹰群。Tent 为一种随机性算子，具有均匀遍历的特点，可以有效地提高初始种群的多样性。Tent 不受初始值的影响，具有更快速的优化和更高效的搜索，因此本文利用 Tent 映射来生成混沌序列[14]。Tent 映射公式为

式中：Xmin为优化空间的下限边界；Xmax为优化空间的上限边界。

采用 Tent 随机算子映射初始化鹰群过程大致包括：随机产生一个N维且每维分量为0 到1 的初始向量Tu，Tu=[Tu1,Tu2,···,TuN]，根据式（7）对Tu进行迭代进化，然后由式（8）将 Tent 映射产生的变量值映射到苍鹰个体上。

1.2.2 种群优化策略

在全局搜索阶段，原始算法中苍鹰的种群数量具有单一性，无法解决全局优化问题[15]。为此本文增加了种群的差异化特征，将苍鹰种群分为鹰王、雌鹰和幼鹰。鹰王作为种群首领要不断地接受挑战和保护自己的领地；雌鹰的主要职责为训练和养育幼鹰，同时也会进行捕食；幼鹰作为一种跟随鹰在成年鹰的保护下生存，同样也挑战鹰王的位置，苍鹰种群优化后，在全局搜索阶段三种苍鹰的位置更新公式为

式中：XNEW,U1为鹰王下一代的全局最优解；gk为第k代的最优解；pk为鹰王迭代过程的历史最优解。γ为付出正态分布的随机数。

1.3 IMNGO 算法验证

1.3.1 IMNGO 算法收敛测试

为了展示IMNGO 算法的优越性，本文在同一基准函数下分别利用自私羊群算法（SHO）[16]、鲸鱼优化算法（WOA）[17]、灰狼算法（GWO）、改进的SHO[18]、改进的WOA[19]和改进的GWO[20]与IMNGO 进行测试。除此之外，为了更进一步展示IMNGO 算法的优越，本文利用不同的基础函数进行对比实验。图1 所示为迭代500 次的收敛曲线图。由于篇幅有限，本文仅展示具有代表性的实验，用到的函数特性如下：

图1 IMNGO 算法收敛对比图

图1a 展示了在f(1)基准函数下SHO、WOA、GWO、NGO 优化算法与IMNGO 优化算法的对比实验。

图1b 展示了在f(1)基准函数下改进的SHO、改进的WOA 和改进的GWO 与IMNGO 优化算法的对比实验。

图1c 展示了在f(2)基准函数下改进的SHO、改进的WOA 和改进的GWO 与IMNGO 优化算法的对比实验。

通过图1 的收敛曲线对比可知，IMNGO 优化算法在收敛速度上要优于未改进的北方苍鹰优化算法以及其他优化算法。例如，GWO 优化算法在测试函数的迭代过程中陷入了局部最优解的问题，而IMNGO 优化算法能够有效地解决这类问题。

同时面对其他类改进的优化算法，IMNGO 具有更快的迭代速度。综上可知，IMNGO 算法对于其他算法来说具有一定的优越性，对数据优化具有一定的可行性。

2 IMNGO-VMD 信号分解

2.1 VMD 基础理论

变分模态分解（variational mode decomposition，VMD）是一种信号处理方法，是完全非递归、自适应的。VMD 信号分解算法具有更加充实的理论基础，该算法的核心要求是构建一个和求解变分的问题。设一个原始信号为f，则它的约束变分表达为

式中：k为分解的模态分量的个数；{wk}、{uk}分别表示经过分解后的第k个中心频率和模态分量；狄拉克系数用 δ(t)表示；*表示卷积运算。为了将约束问题转换成为非约束问题，选择引入拉格朗日乘法算子λ。最终的VMD 分解流程为

①初始化 {uk}、{wk}、λ和最大迭代次数N。

②更新{uk}、{wk}、λ。

③根据式（18）判断精度，若不满足则返回第二步，满足则停止迭代。

式中：ε＞0，n＜N。

2.2 IMNGO 优化VMD 流程

利用改进的北方苍鹰优化算法（IMNGO）对VMD 参数进行优化。在传统的VMD 中，当分解层数k较小时，信号分解可能不充分。趋势项可能与其他干扰项混合，导致包络熵变大。当取合适的k值时，趋势项的包络熵变小。因此，该算法在VMD 优化过程中使用包络熵作为适应度函数。当分解信号中的最小熵（局部包络熵）最小时，VMD 分解是最优的。VMD 参数优化过程如图2 所示。首先初始化种群的位置向量[k,α]，以包络熵为适应度函数计算每只北方苍鹰的适应度，然后通过判断收敛因子，选择一个迭代公式进行迭代更新，直到满足终止条件，输出最优参数。

图2 优化流程图

图2 所示为加入IMNGO 优化算法的VMD 分解流程。接下来本文采用模拟信号对VMD 进行优化测试，为了对比IMNGO 算法彰显出的优势，本文将改进的SHO、改进的WOA 和改进的GWO 优化算法来优化VMD 进行测试。收敛效果如图3所示。

图3 优化VMD 收敛图

通过算法优化VMD 的收敛图可知，算法在经历500 次迭代后都达到了各自的最优迭代值。但是，IMNGO 算法相在一定程度上也避免了局部最优的现象出现，IMNGO 算法对比其他优化算法更加具有优势和可行性。

3 实验验证

3.1 实验数据

此次实验数据采用网上模拟工作台采集3 种故障轴承信号和正常信号用来验证算法。该平台为在线仿真平台。主要包括实验所需的电机轴承、平台支撑架、信号波形显示器、轴承模拟故障工作区和数据传输线等，平台可实现实验所需故障信号的采集。实验用滚动轴承型号2612（单列向心短圆柱滚子轴承）基本尺寸：滚动体直径d=18 mm、接触角a=0、滚动体个数z=12、节圆直径D=95 mm、涡流位移传感器测得主轴转速n=1 045 r/min、加速度仪采样频率f=1 024 Hz，该数据包括正常信号、内圈故障信号、外圈故障信号和滚动体轴承信号。

3.2 信号处理

3.2.1 IMNGO 算法性能测试

为了验证IMNGO 算法的性能，本文选取具有代表性的优化测试函数Damavandi。利用IMNGO算法、改进的SHO、改进的WOA 和改进的GWO对Damavandi 测试函数优化50 次，并进行比较。Damavandi 测试函数为

Damavandi 测试函数的全局最小值为0，局部最小值为2。将50 次优化结果的优化均值和标准差绘制成表1。

表1 各算法优化性能

通过图4 和表1 可知，IMNGO 算法在对测试函数50 次的优化过程中，数值的波动最小。优化数值的标准差优于改进的SHO、GWO、WOA 算法，优化性能得到了明显的提升。

图4 50 次算法优化结果

3.2.2 轴承数据处理

本文将提取的4 种故障信号进行IMNGO 算法优化分解。以内圈故障信号为例，通过IMNGO 来优化VMD 找到最佳的分解层数。经过IMNGO 算法优化可知最佳分解层数k为10 层，最优的alpha值为2 000，最优的适应度值为0.340 6，如图5 所示。

图5 内圈故障信号优化分解

为了最大程度地展示IMNGO 算法的优越性。本文将IMNGO 算法优化分解后的本征模态分量（IMF）通过希尔伯特边际谱展示，图6 所示为传统VMD 分解后的希尔伯特边际谱。

图6 VMD 分解的希尔伯特边际谱

通过图6 和图7 可以发现，内圈故障发生的主要频域为231 Hz、275 Hz、298 Hz。但是经过IMNGO 算法优化后，主要发生故障的频率为215 Hz、233 Hz、275 Hz、286 Hz、307 Hz。经过对比可以发现，优化后分解的IMF 分量故障特征更为完善，对故障信号的分解更为细致，有利于提高对故障的识别准确率。

图7 本文方法分解的希尔伯特边际谱

将IMNGO 优化后的IMF 分量构建特征向量能量谱，以内圈故障信号为例，图8 所示为分解的10 组特征向量。利用主元素分析法对每个IMF 分量进行主元贡献率的计算，如图9 所示。

图8 内圈故障能量谱

图9 4 种故障信号的主元贡献图

通过特征向量能量谱和主元贡献图可知，IMF分量在第8 层后的贡献不是很大。前8 层的累计贡献率达到了98%以上，所以本文选取前8 层IMF分量用于实验。

3.3 单工况实验验证

作为将信号进行筛选分类的一种算法模型，SVM 也可以处理非线性分类的问题。本文将利用SVM 对机械轴承的故障信号进行分类识别。为了更好地训练，接下来将4 种故障信号的实验数据进行编号，结果见表2。

表2 故障编号表

在进行轴承故障数据的训练前先划分数据集，本文将单工况数据的前90%（2 241 组）作为训练集，后10%（249 组）作为测试集。数据划分结束后将数据导入到SVM 模型中进行训练并测试。

本文在优化VMD 信号分解流程的基础上将IMNGO 算法用于优化SVM 参数，并使用优化后的SVM 进行识别。识别结果如图10 所示。

图10 单工况传统方法测试效果图

通过图10 和图11 对比可知，在4 种故障检测上，相比于传统的检测方法，利用IMNGO 算法优化后得到的识别结果更加准确。使用IMNGO 算法优化后，在正常状态、外圈故障和滚动体故障上，3 种故障的识别准确率达到了100%。

图11 单工况IMNGO 优化后测试效果图

本文为了进一步对比IMNGO 算法的优越性，将改进的SHO、改进的WOA 和改进的GWO 与IMNGO 优化算法用来优化VMD 和SVM，并展示优化后的测试结果，绘制成表3。

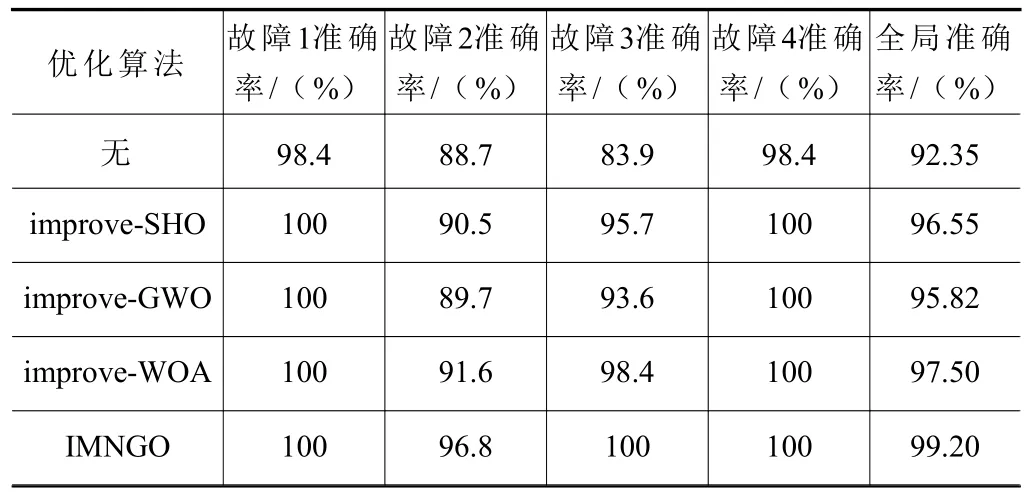
表3 单工况测试集效果汇总表

由表3 可知，在使用其他相关算法优化VMD和SVM 过程中，相较于传统的检测方法准确率有所提升。但是，本文提出的IMNGO 算法优化后的识别准确率提升最为明显。

3.4 复杂工况实验

本文将复杂工况数据的前90%（972 组）作为训练集，后10%（108 组）作为测试集。数据划分结束后将数据导入到SVM 模型中进行训练并测试。

由图12 和图13 可知，传统的检测方法在复杂工况下的识别准确率降低了很多，内圈和外圈故障的识别准确率降到了81.5%，但是，通过IMNGO算法优化后，内圈和外圈的故障识别准确率分别提升了7.4%和11.1%。滚动体故障的识别准确率甚至达到了100%。

图12 复杂工况传统方法测试效果图

图13 复杂工况IMNGO 优化后测试效果图

由表4 可知，在复杂工况下，其他相关算法在优化VMD 和SVM 过程中，对故障的识别准确率并没有得到较为理想的提升，改进的WOA 算法对故障1 的识别准确率和改进的SHO 算法对故障2的识别准确率还有所下降。但是，利用本文提出的IMNGO 算法优化后，4 种轴承故障的识别准确率都得到了提升。

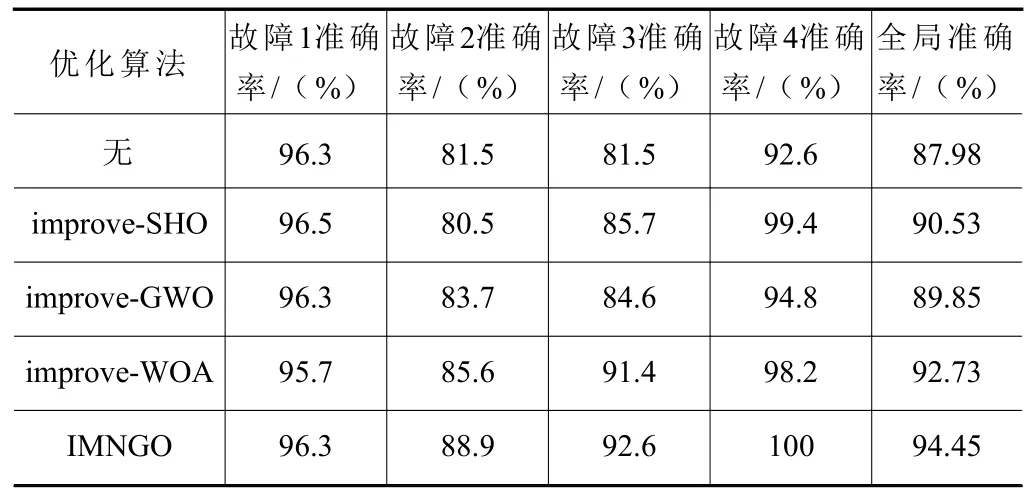
表4 复杂工况测试集效果汇总表

4 结语

（1）本文通过实验结果证明小样本数据下IMNGO 优化算法去优化VMD 和SVM 的可行性，表明了IMNGO 优化算法的性能比NGO 和其他算法的优化算法性能有所提升。

（2）在小样本数据下对VMD 进行优化时能够最大程度的提取信号特征，提升后续的检测识别准确率。单工况下，传统的VMD 融合SVM 全局识别准确率为92.35%，本文提出的IMNGO 算法优化后的VMD 和SVM 识别准确率相比于传统方法提升了6.85%。复杂工况下，传统的VMD 融合SVM全局识别准确率为87.98%，本文提出的IMNGO 算法优化后的VMD 和SVM 识别准确率相比于传统方法提升了6.47%。该方法为小样本数据的轴承故障识别提供了新思路，为设备轴承的故障识别提供了新方法。